一种改进的果蝇优化算法求解连续函数优化问题
2016-06-02杨立君付雅琴殷旅江邓义成
杨立君,付雅琴,殷旅江,邓义成
(1.湖北汽车工业学院经济管理学院,湖北十堰442002;2.上海海事大学经济管理学院,上海201306)
一种改进的果蝇优化算法求解连续函数优化问题
杨立君1,付雅琴1,殷旅江1,邓义成2
(1.湖北汽车工业学院经济管理学院,湖北十堰442002;2.上海海事大学经济管理学院,上海201306)
摘要:在原始果蝇算法基础上,结合经典粒子群算法,设计了新的粒子速度和种群更新方法,提出了一种新的改进果蝇算法,然后将改进果蝇算法应用于连续函数优化问题,并用标准测试函数进行了验证,最后对改进果蝇算法的优化机理进行了分析。
关键词:果蝇算法;粒子群算法;函数优化
oi:10.3969/j.issn.1008-5483.2016.01.016
果蝇优化算法(Fruit Fly Optimization Algo⁃rithm,FOA)是由台湾学者潘文超在研究了果蝇的觅食行为后,结合达尔文的进化论,于2011年提出的一种新型智能优化算法[1]。这类智能优化算法还有许多,比如遗传算法(GA)[2]、蚁群算法[3]、粒子群算法(PSO)[4]等。这些算法提出较早,并且已经被应用与诸多领域。而果蝇算法是近几年提出的,目前的研究主要是在对该算法的改进[5-7],以及解决多维背包问题[8]等问题上。
原始果蝇优化算法用于求解一般简单函数的极值等问题时可以取得较好的效果,但对于较复杂函数问题的求解,尚存在一定的缺陷,比如收敛精度不高、易于陷入局部最优解等,而目前对于果蝇优化算法的一些改进研究也是改变部分编码方式[7]或者引入新参数[6]等,算法性能未得到实质性改进,这也制约了果蝇算法的进一步发展与应用。
函数优化问题在管理决策、工程控制等问题中比较常见。优化函数也是多种多样的,但是大多以连续型函数为主。国内外学者借助现今先进的科学技术和工具,将遗传算法、蚁群算法、粒子群算法等应用于该类问题上,取得了较好的效果,但是也存在一些问题。本文通过一步步的分析论证,发现了原始果蝇算法尚存在的不足,然后提出一种改进的果蝇优化算法,并通过一些标准测试函数,验证了改进果蝇算法,实验结果显示该新算法在求解函数优化问题上的优越性。最后总结了改进果蝇算法的优化机理。
1 原始果蝇算法原理
果蝇优化算法是在研究了果蝇觅食行为后,结合进化论提出的一种寻求全局最优解的智能新算法。果蝇具有很敏锐的嗅觉,可以很好地搜集到空气中漂浮的各种气味,并迅速飞往食物处。根据果蝇的这一特性,对果蝇算法进行了总结。图1为果蝇群体迭代搜索示意图。
总结来说,果蝇算法首先随机初始化种群,然后利用适应度函数比较果蝇味道浓度,接着所有果蝇飞向味道浓度最佳的果蝇位置,并继续新的种群变异,最终飞向最优解。
为提高原始果蝇算法的搜索效率,许多学者对该算法进行了拓展和改进,比如利用嗅觉缩小搜索半径[5],给予一个新的距离函数[7]等。这些改进取得了一定效果,但是这些改进并未触及到果蝇算法的本质。以简单函数Y=3-x2和Y=3-(x+2)2为例,这2个函数的最大值应该都是3,由图2可知,函数Y=3-x2可以获得最优解3,然而对于函数Y=3-(x+ 2)2,却无法得到最优解。对于这类简单的函数求极值问题,果蝇算法虽然有许多优点,但是仍未取得理想的效果,这是由于原果蝇算法步骤中味道浓度判定函数Si=1/Di使得果蝇搜索空间只能为正值部分。因此提出了优化的果蝇算法。
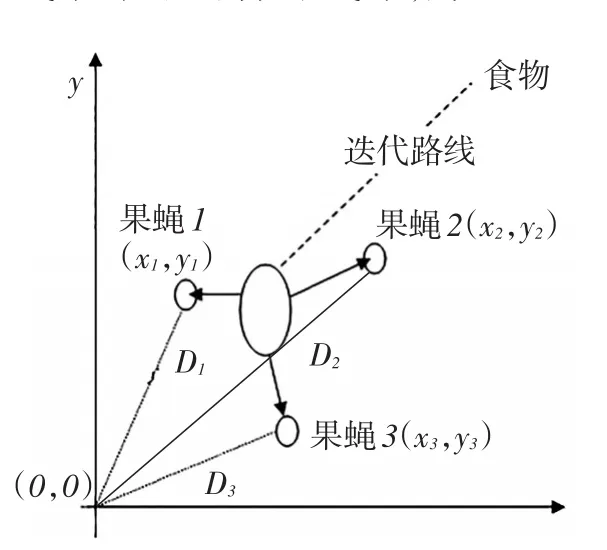
图1 果蝇群体迭代搜索示意图

图2 函数结果图
2 改进果蝇算法求解函数优化问题
2.1改进果蝇优化算法思想和模型
以几个简单函数的求极值问题为例,发现原始果蝇算法存在着解的搜索域不能为负值域,以及在搜索过程中容易陷入局部最优解等不足。本文中提出的改进果蝇算法与原始果蝇算法不同,该算法以原始果蝇算法为基础,结合了粒子群算法,这样可使2种算法优势互补,从而在解决函数优化问题上获得较好效果。
本文中改进果蝇算法的思想是不再使用原算法中的距离倒数作为果蝇味道浓度判定函数,而是在进行种群初始化的同时,赋予优化粒子一个初始速度,从而扩展了解的搜索空间,提高了解的搜索速度,其模型基本步骤如图3所示。
2.2初始化
首先设置参数,比如进化次数、种群数目、种群位置、粒子初始速度等。在进行种群位置初始化时,采用随机定义种群位置的方法,这使得初始种群具有一定的分布性,有较大概率覆盖解的搜索空间,从而易于获得最优解。同时新引入一个粒子速度的初始化,可以极大地加速解的搜索效率。

图3 改进果蝇算法优化模型图
2.3新的进化方法
在该方法进化迭代过程中,迭代寻优时外层采用果蝇算法循环,内层为粒子群算法的循环。在循环过程中,内层循环是果蝇使用粒子群算法的更新方法,不断进行自我更新和局部搜索,而外层循环则继续使用果蝇的嗅觉和视觉进行全局搜索,最后获得最优解。
2.4改进果蝇算法步骤
改进果蝇优化算法程序伪代码如下:
Algorithm:theimprovedfruitflyoptimization algorithm
Parameter: maxgen , maxgenpso,sizepop Output: optimal solution yy 1.initialize
Set maxgen , sizepop , maxgenpso,particle
initial location and initial speed of particle
FOR i=1 to sizepop
pop(i,:) = LBj +(UBj -LBj)*rand(1,n)
V(i,:)=rand(1,n)
END FOR
2.compare the fitness and get the extreme value of individu⁃al and global(gbest and zbest)zbest=pop (bestin dex,:) gbest=pop
3.update the speed and population V(j,:)=w×V(j,:)+cl×rand(1,n)×gbest(j,:)-pop(j,:))+ c2×rand×(zbest-pop(j,:)
pop(j,:)=pop(j,:)+0.5×V(j,:) 4.update the extreme value of individual and global
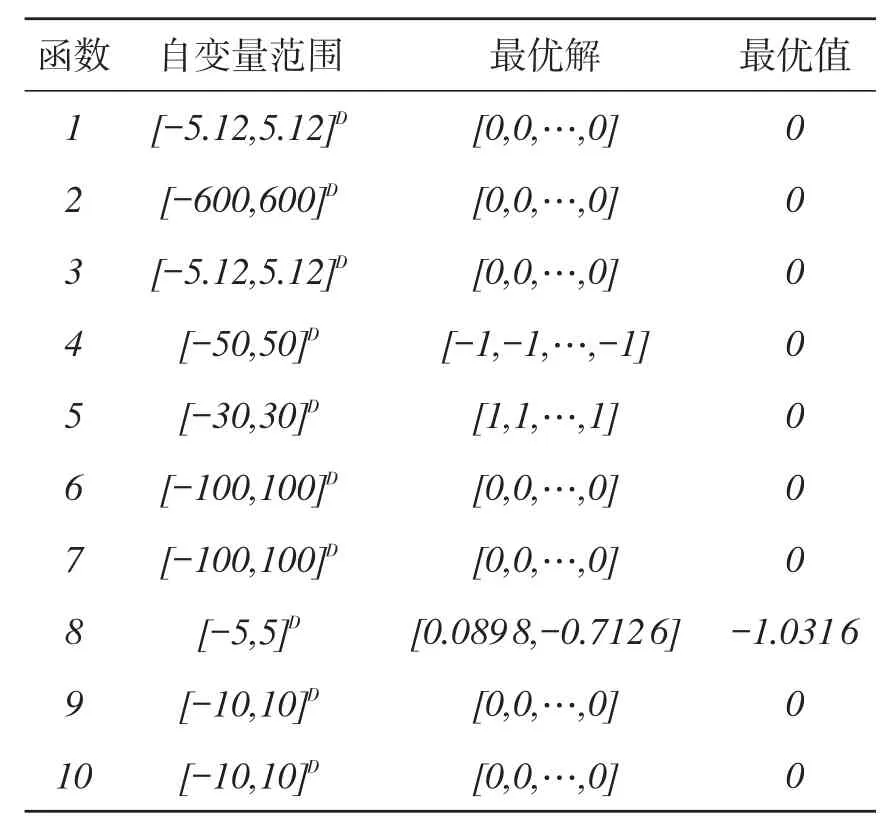
IF fitness(j) gbest(j,:)=pop(j,:) END IF IF fitness(j) zbest=pop(j,:) END IF 5.calculate the fitness and output yy gen定义为果蝇算法进化次数,genpso定义为粒子群算法进化次数,sizepop定义为种群数目,V为粒子速度,w,c1,c2均为自定义变量。 3.1测试函数基本信息 随机选取几个标准测试函数,由于不同类型测试函数特征不同,因此可以通过比较不同算法的运行结果,来得到改进果蝇算法的一些性能。函数全局最优解以及对应的最优值如表1所示。 表1 测试函数的基本信息 3.2实验基本参数设置 为了检测本文中提出的改进果蝇算法的性能,并且同原果蝇算法进行比较分析,需要2种算法的运行环境相同,以利用文中使用的几个测试函数来进行测试。算法的基本参数gen为200次,genpso 为400次,sizepop为30个。 3.3实验结果 对原算法和改进算法结果进行比较与分析。每个测试函数运行30次后测试结果分析见表2。在运行环境相同的条件下,对于函数7~8来说,由于其适应度地形比较平坦,所以对于这类问题,2种算法均可以取得很好的效果。对于函数1,2,4来说,改进后算法求得结果的均值和标准差均明显小于原算法,很好地说明了改进后算法在解决这类问题上具有较好的收敛精度和收敛可靠性。对于其他几个函数(函数6除外)来说,改进算法的结果在收敛精度和收敛可靠性上有一定优势。总体来说,改进算法具有更好的收敛可靠性和实用性。 式中:w为权重;c1,c2为加速因子,通常为常数。 本文中提出的改进算法优化机理步骤如下: 步骤1果蝇从个体极值获得部分更新信息。式(1)中[c1×rand(1,n)×(gbest(j,:)-pop(j,:))] 表示果蝇通过个体极值获得更新信息,c1*rand表示其信息继承度。 步骤2果蝇从全局极值获得部分更新信息。式(1)中[c2×rand(1,n)×(zbest-pop(j,:))] 即表示果蝇通过全局极值获得更新信息。 步骤3果蝇进行局部随机搜索过程,即2、4节中的内层循环过程。式(1)中w×V(j,:)表示果蝇在获得更新信息后的自我更新。w表示对全局搜索和局部搜索的平衡,令 w= maxw-((maxw-minw)/maxgenpso)×1使其具有较合理的平衡能力。 对原始果蝇算法存在的局限性进行了分析,然后在原算法基础上,结合粒子群算法,提出一种新的改进果蝇算法,并对其进行了详细介绍。通过10个测试函数,比较了改进算法和原算法的运行结果,实验结果表明:改进算法具有较好的收敛性 与较好的寻优能力,验证了改进果蝇算法在求解函数优化问题上的可行性和优越性。下一步,可以探讨将改进果蝇算法应用于元胞遗传算法[9]、模糊聚类问题当中[10],以扩展期应用范围。 参考文献: [1]潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报,2011,29 (4):1-5. [2]贺巧龙,李东亮.基于遗传算法的函数优化问题研究[J].软件导刊,2009,8(6):71-72. [3]赵文彬,孙志毅.蚁群算法在一般函数优化求解中的应用[J].太原科技大学学报,2005,26(3):210-212. [4]郭志辉,张远平.一类函数优化问题的求解[J].科学技术与工程,2009,9(13):3634-3637. [5]Yuan Xiaofang, Dai Xiangshan, Zhao Jingyi, et al. On a Novel Multi-swarm Fruit Fly Optimization Algorithm and Its Application[J]. Applied Mathematics and Computa⁃ tion,2014,233(3):260-271. [6]Pan Quanke, Sang Hongyan, Duan Junhua, et al. An Im⁃proved Fruit Fly Optimization Algorithm for Continuous Function Optimization Problems[J]. Knowledge- Based Systems,2014,62(5):69-83. [7]Dai Hongde, Zhao Guorong, Lu Jianhua, et al. Comment and Improvement on“A new Fruit Fly Optimization Algo⁃rithm: Taking the Financial Distress Model as an Exam⁃ple”[J]. Knowledge-Based Systems,2014,59:159–160. [8]Wang Ling, Zhen Xiaolong, Wang Shengyao. A Novel Bi⁃nary Fruit Fly Optimization Algorithm for Solving the Multi Dimensional Knapsack Problem[J]. Knowledge-Based Systems, 2013,48(2):17-23. [9]殷旅江,高亮,李登桥,等.改进元胞遗传算法的转塔式贴片机贴装优化[J].华中科技大学学报(自然科学版),2015(3):113-117+132. [10]殷旅江,杨立君,胡明茂,等.基于混合遗传模拟退火的模糊C-均值聚类算法[J].湖北汽车工业学院学报,2015(3):62-65.务解答,也接受消费者在实体经销商处消费后对服务的咨询。对于网络订单,会产生订单在生产期间被取消的风险。针对此问题,网络销售时可考虑让消费者支付一部分定金,如果中途取消订单,将会扣除一部分定金。对于产品的交付,东风创普可以根据消费者提供的地址,联系最近的经销商,由经销商联系消费者提车付全款,然后东风创普后期再补给经销商车辆。这样可以从一定程度上减少网络销售的风险,也缩短用户交付周期,提升服务质量和提高顾客满意度。 营销渠道策略已成为汽车企业获取长期竞争优势的重要手段,因此东风创普应结合市场环境的变化对渠道方案作出相应的调整和优化,尤其是在经济新常态和互联网背景下,如何打造高效、有竞争力的营销渠道,使得网络渠道和实体渠道相得益彰,已成为东风创普下一步需要重点研究的课题。 [1]邓海燕.汽车营销渠道优化分析[J].中国外资,2012 (23):44. [2]宁文祥.全球商用车市场依然在上升轨道上[J].专用汽车,2012(8):42-43. [3]黄国祥,李乃和,杨洪涛.渠道成员绩效的评估[J].上海管理科学,2012(6):25-28. [4]王秀丽.东风商用车营销渠道冲突及对策研究[J].湖北汽车工业学院学报,2006(4):78-80. [5]张广玲,李伟.企业渠道冲突解决研究:一个整合的视角[J].珞珈管理评论,2012(2):20-26. [6]王秀丽.东风标致营销渠道冲突及对策研究[J].湖北汽车工业学院学报,2015(4):66-70. ? An Improved Fruit Fly Optimization Algorithm in Solving Continuous Function Optimization Problem Yang Lijun1, Fu Yaqin1, Yin Lüjiang1, Deng Yicheng2 (1. School of Economics and Management, Hubei University of Automotive Technology, Shiyan 442002, China; 2. School of Economics and Management, Shanghai Maritime University, Shanghai 201306, China) Abstract:On the basis of the original fruit fly algorithm, a new improved fruit fly algorithm was pro⁃posed by combining with classical particle swarm optimization algorithm, and designing the new parti⁃cle velocity and the new update way of population. Then the improved algorithm was used in solving continuous function optimization problem, and the reliability and advanced nature of the proposed algo⁃rithm were verified by takingseveral standard test functions. The algorithm mechanism was analyzed. Key words:fruit fly algorithm; particle swarm optimization algorithm; function optimization 作者简介:杨立君(1962-),男,湖北十堰人,教授,主要从事生产与运作管理、物流与供应链管理方面的研究。 基金项目:教育部人文社会科学研究规划基金项目(14YJA630079);湖北省自然科学基金指导性计划(2015CFC787);湖北省教育厅科学技术研究项目(Q20151801) 收稿日期:2015-11-12 中图分类号:TP18 文献标识码:A 文章编号:1008-5483(2016)01-0071-04 d3 仿真实验与结果

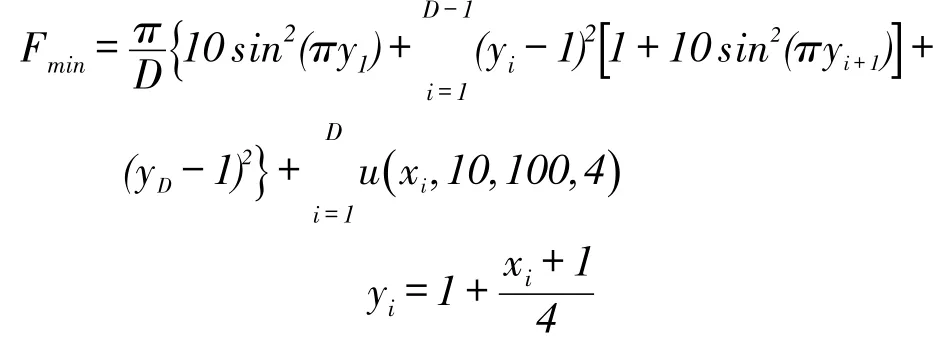

4 改进果蝇算法优化机理分析
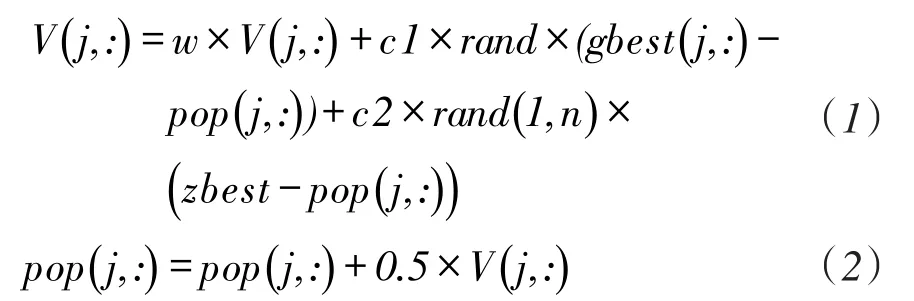
5 结论
5 结束语
