Banach空间中线性离散时间系统的非一致幂稳定性

岳田

（湖北汽车工业学院理学院，湖北十堰442002）



Banach空间中线性离散时间系统的非一致幂稳定性

岳田

（湖北汽车工业学院理学院，湖北十堰442002）

摘要：给出了Banach空间中线性差分方程的非一致幂稳定性的若干刻画，推广了幂不稳定性及指数稳定性中的相关经典结论。

关键词：非一致幂稳定性；线性离散时间系统；Lyapunov序列

0　引言

由于在动力学中指数稳定的条件相对较强，因此有必要寻找一个较为一般的稳定渐近行为。最近Popa等人在文献［9］中给出了线性离散时间系统非一致幂不稳定性的定义，并研究了其离散性质。在其启发下，本文中将给出线性离散时间系统非一致幂稳定性的概念，并给出其相应性质的刻画，从而将指数稳定性［8］及幂不稳定性［9-10］中相关经典结论推广到了非一致幂稳定性的情形。

1　记号及预备知识

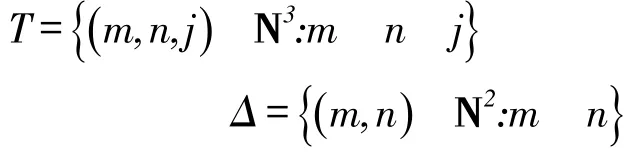
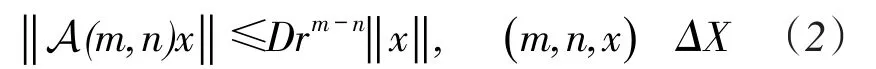
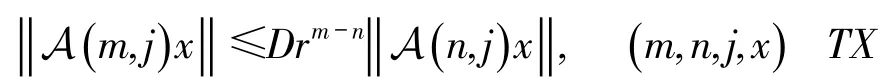
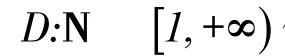
显然，若线性离散时间系统（1）是一致幂稳定的则它一定是非一致幂稳定的，反之不一定成立。

总之，将网络教学平台运用到职校数学教学中，需要教师不断提高自身的业务水平，与时俱进，掌握使用各种平台的能力。教师研究教学内容、平台功能来备课，恰当地运用平台，并把网络教学平台、教学资源和教学行为进行有机整合，为学生的自主学习提供更大的灵活性，不再受空间和时间的约束。如果网络教学平台能更好地为职校数学教学实践服务，那么必然会为职校数学教学开辟一条新的道路。

2　主要结论

引理1线性离散时间系统（1）是非一致幂稳定的，当且仅当存在2个非减序列

证明类似文献［9］中的证明。

推论1线性离散时间系统（1）是一致幂稳定的，当且仅当存在非减序列且满足，使得

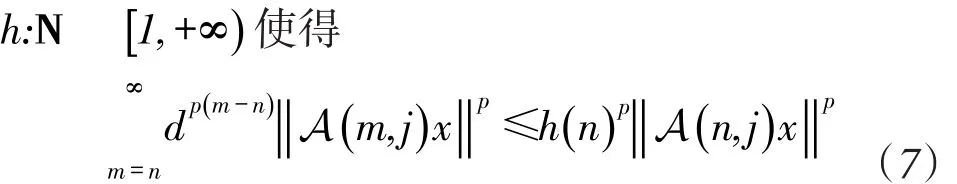
推论3线性离散时间系统（1）是一致幂稳定的，当且仅当存在常数，使得

定理2线性离散时间系统（1）是非一致幂稳定的，当且仅当存在Lyapunov序列L及非减序列，使得

进而利用引理1可知系统（1）是非一致幂稳定的。

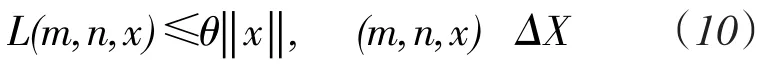
参考文献：

［1］Datko R. Extending a Theorem of A.M. Liapunov to Hil⁃bert Space［J］. JMath Anal Appl, 1970, 32（3）: 610-616.

［2］Pazy A. Semigroups of Linear Operators and Applications to Partial Differential Equations［M］. New York：Spring⁃er, 1983.

［3］Datko R. Uniform Asymptotic Stability of Evolutionary Processes in a Banach Space［J］. SIAM J Math Anal, 1973，3（3）: 428-445.

［4］Rolewicz S. On Uniform N-equistability［J］. J Math Anal Appl, 1986, 115（12）: 434-441.

［5］Neerven J M A M. Exponential Stability of Operators and Semigroups［J］. JFunct Anal, 1995, 130（2）: 293-309.

［6］Preda P, Pogan A, Preda C. Functionals on Function and Sequence Spaces Connected with the Exponential Stabili⁃ty of Evolutionary Processes［J］. Czech Math J, 2006, 56 （2）: 425-435.

［7］Stoica C, Megan M. On Uniform Exponential Stability for Skew- evolution, Semiflows in Banach Spaces［J］.Car⁃pathian Journal of Mathematics, 2013, 29（2）：259-266.

［8］Popa I L, Ceausu T, Megan M. On Exponential Stability of Linear Discrete- time Systems in Banach Spaces［J］. Comput Math Appl, 2012, 63（11）: 1497-1503.

［9］Popa I L, Ceausu T, Megan M. Nouniform Power Instabili⁃ty and Lyapunov Sequences［J］. Appl Math Comput, 2014, 247: 969-975.

［10］Popa I L, Ceausu T, Megan M. A Note on Power Instabil⁃ity of linear Discrete- time Systems in Banach Spaces ［J］. Computers & Mathematics with Applications, 2012, 63（11）: 83-89.

Nonuniform Power Stability for Linear Discrete-time Systems in Banach Spaces

Yue Tian
（School of Science, Hubei University of Automotive Technology, Shiyan 442002, China）

Abstract:Several characterizations for the nonuniform power stability of the linear difference equations in Banach spaces were given. The well-known results for the power instability and the exponential sta⁃bility were extended.

Key words:nonuniform power stability; linear discrete-time system; Lyapunov sequence

作者简介：岳田（1988-），男，四川南江人，硕士，主要从事微分系统稳定性的研究。E-mail：ytcumt@163.com

基金项目：湖北省自然科学基金（2014CFB629）；湖北汽车工业学院预研基金（2014XY06）

收稿日期：2015-09-29

doi：10.3969/j.issn.1008-5483.2016.01.016

中图分类号：O175.13

文献标识码：A

文章编号：1008-5483（2016）01-0064-03