对称法在高考问题解决中的应用

董茂寅

摘 要：科学方法有很多种，利用科学方法处理问题可以提高效率。本文以对称法为例，指出利用对称法解题的思路和方法，根据高考试题中出现的对称问题，从物理图形、运动轨迹、物理图像、物理过程等几个方面剖析了对称法与高考命题的相关性，展示如何应用对称法解决高考问题。

关键词：对称法；高考试题；问题解决

对称法就是根据某些物理情境中的几何图形、物理现象、物理规律、物理过程的对称性进行命题、解题的一种科学方法，利用对称法分析解决问题可以避免复杂的数学演算和推导，直接抓住问题的实质，有出奇制胜、事半功倍之效。一般来说利用对称法解题可以按如下步骤进行。

首先，审视物理情境，选取研究对象。在仔细审题的基础上，选取恰当的研究对象，如运动的物体、运动的某一过程或某一状态。通过题目的背景、条件、设问，深刻剖析物理现象及过程，建立清晰的物理情境。

其次，缜密分析研究对象的性质（包括图形、图象以及所处的物理环境，如接触面情况，场的分布等）、运动特点（包括运动轨迹、运动过程）及规律（包括过程规律、状态规律以及前后过程和状态间的联系等）。

再次，寻找研究对象的对称性特点。在已有经验的基础上通过直觉思维，或借助对称原理的启发进行联想类比，分析研究对象在某些属性上或运动过程、规律变化上的对称性。这是解题的关键环节。

最后，利用对称性的特点，依据物理规律列解方程，得出物理结果。

一、物理图形对称

在一些高考试题的命制过程中，命题者有时设计一些对称的图形，这些图形或关于某一点对称，或关于某一条直线对称，或关于某一个平面对称，而解题时，可以利用这些对称性来发现解决问题的突破口，迅速解决问题。

点评：解本题有两个关键，一是求B星体所受得合力，在求B星体所受得合力时，由于不是直角三角形，要采取欲合先分的方法，先进行正交分解再利用合成法。二是确定轨道半径，由于B、C两星体的质量均为m，其两星体的质量中心在其连线的中点，故圆心应位于质量的中心，即AD的中点，根据几何关系确定圆心的位置、利用勾股定理或对称性、力的三角形和几何三角形的关系確定轨道半径。

二、运动轨迹对称

物体的运动轨迹有时出现对称，利用其对称性分析解决问题，有时能起到破题的作用，也能起到事半功倍的效果。

点评：利用运动轨迹的对称性命题，利用运动轨迹的对称性把运动过程分为连续相等的过程，利用分运动的运动特点确定连续相等的时间。

三、物理图像对称

在应用数学图象表达物理规律时，有的图象关于坐标原点对称，有的关于x轴对称，有的关于y轴对称，有的关于某一条直线对称，在解决高考问题是时，有时利用对称性解决问题可能起到出奇制胜的效果。

例3（2013年上海-13）如图，足够长的直线ab靠近通电螺线管，与螺线管平行。用磁传感器测量ab上各点的磁感应强度B，在计算机屏幕上显示的大致图像是

答案：C

解析：通电螺线管外部中间处的磁感应强度最小，所以用磁传感器测量aO上各点的磁感应强度B的变化先增大后减小，由对称性可知，图象关于y轴对称，故选项C正确。

点评：本题考查了通电螺线管周围的磁感应强度的分布规律，根据对称性命题，利用对称性解决问题。

四、物理过程对称

物理研究对象在状态变化过程中，有时候后一个物理过程与前一个物理过程具有相似性或对称性。也有的物理问题涉及可逆物理过程，当按正常思路判断求解时可能束手无策，但若运用逆向思维方法来分析、判断，利用物理过程或可逆物理过程的对称性来解题，是培养思维能力的另一捷径。

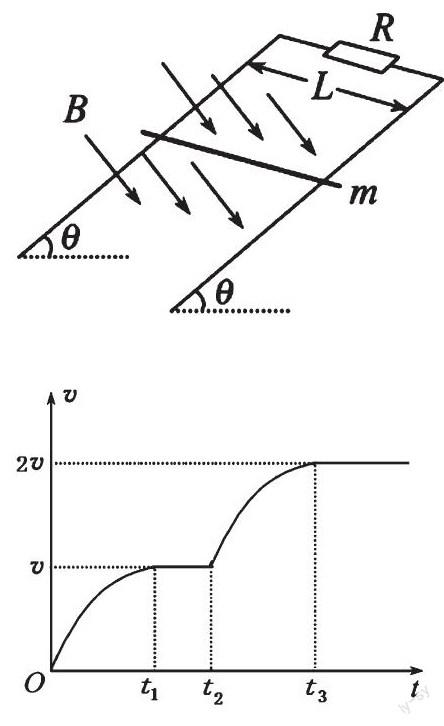
例4（2012年山东-21）如图所示，相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ，上端接有定值电阻R，匀强磁场垂直于导轨平面，磁感应强度为B。 将质量为m的导体棒由静止释放，当速度达到v时开始匀速运动，此时对导体棒施加一平行于导轨向下的拉力，并保持拉力的功率恒为P，导体棒最终以2v的速度匀速运动。导体棒始终与导轨垂直且接触良好，不计导轨和导体棒的电阻，重力加速度为g。下列选项正确的是（ ）

A.P=2mgvsinθ

B.P=3mgvsinθ

C.当导体棒速度达到 时加速度大小为sinθ

D.在速度达到2v以后匀速运动的过程中，R上产生的焦耳热等于拉力所做的功

当速度达到2v以后匀速运动的过程中，R上产生的焦耳热等于拉力和重力所做的功之和，D错。

点评：根据导体棒的运动情况，对导体棒进行正确受力分析，结合安培力公式，利用能量守恒定律求功率，分析焦耳热；利用牛顿第二定律求加速度。发现物理过程、物理图像的对称性，根据对称性推理对称的物理过程应该遵循相同的规律，这是解题的突破口。