多边形内角和定理适用性讨论

金震宇

一、前 言

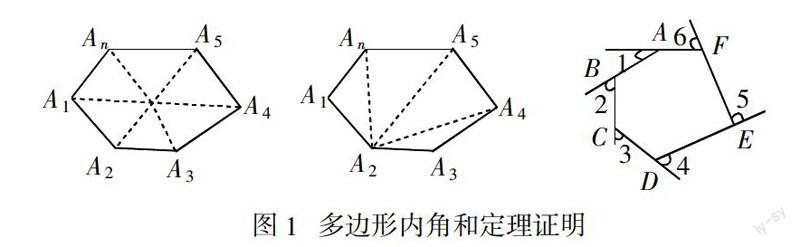
多边形内角和定理为：n多边形内角和 = （n - 2）180°，n多边形外角和 = 360°，其证明源于三角形内角和 = 180°. 如图1所示，在凸多边形中借助辅助线引入适量三角形，使原多边形内角和转化为引入诸三角形内角和，从而得证. 其证明细节请参看文献[1].

因为凸多边形一个顶点对应一条边，所以可数它有多少暴露出的顶点数求出较复杂凸多边形边数. 但是我在做题中发现，有类问题无论是数边还是数顶点求出的结果都出错. 这引起我兴趣，故写出来与大家讨论.

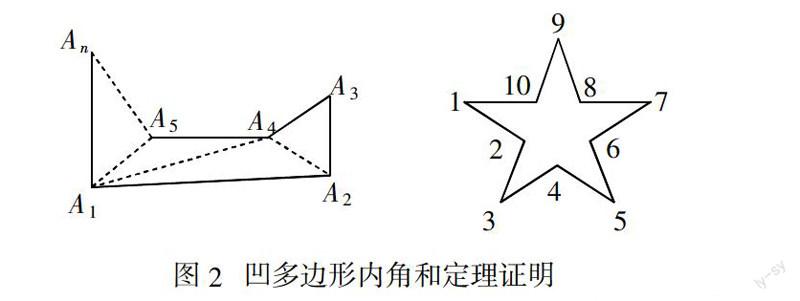
二、多边形内角和定理仅适用于凸多边形和凹多边形

三、多边形内角和定理不适用于出现交叉线的多边形

请先看图3左图，这是有交叉线四个顶点最简单图形，若用多边形内角和定理，其内角和为360°. 这显然不是角∠A + ∠B + ∠C + ∠D之和，题中多算了∠1 + ∠2，而∠1或∠2的具体数值不确定，仅据 ∠1和∠2为对顶角，可已得到：∠A + ∠B = ∠C + ∠D，故∠A + ∠B + ∠C + ∠D之和无解.

四、结 论

多边形内角和定理仅适用于凸多边形和凹多边形，它不适用有交叉线图形，解题时若遇到有求交叉线图形求多角和时，要依平面儿何诸定理知识，设法把问题转化为求凸多边形或凹多边形内角和，使问题得解.

【参考文就】

[1]数学，七年级下册[M].江苏科学技术出版社，2012年11月第3版，P31-35.

[2]学习与评价，数学测试卷，七年级下，第7章[M].江苏凤凰出版社.