某类系统谱的上界

吴 平(苏州市职业大学 数理部，江苏 苏州 215104)



某类系统谱的上界

吴 平
(苏州市职业大学 数理部，江苏 苏州 215104)

摘 要：根据Rayleigh定理、分部积分和不等式估计等方法，得到系统谱(特征值)的上界的不等式，其结果在数学、物理和力学等学科中有着广泛的理论研究和应用价值.

关键词：某类系统；谱；上界；不等式

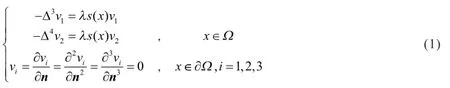
其中μ1，μ2是正实数.由相关方程理论知，问题(1)的谱是离散的，且都是正实数.设

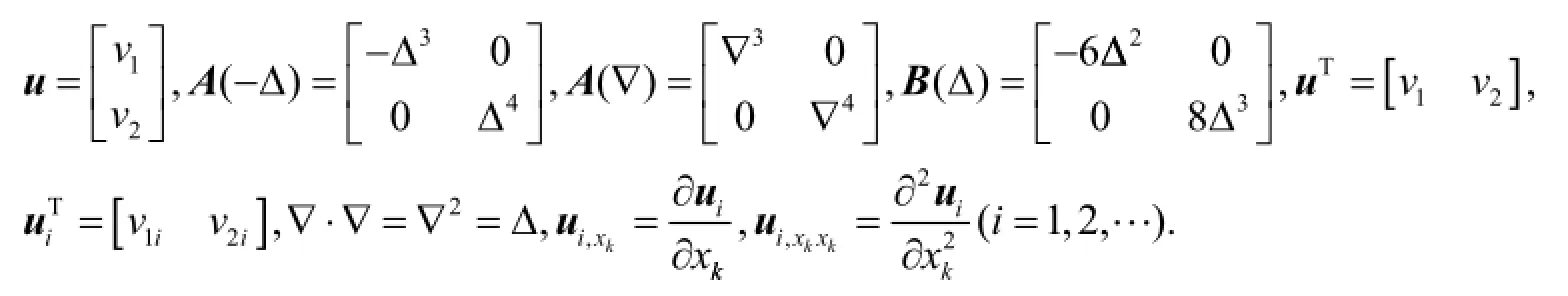
问题(1)可写成如下矩阵形式

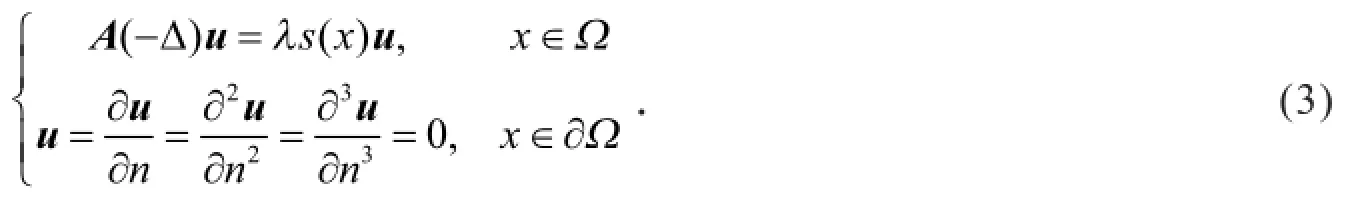
设问题(3)的特征值为0≤λ1≤λ2≤…≤λn≤…，与之对应的带权s(x)正交规范特征向量为u1，u2，…， un，…，满足

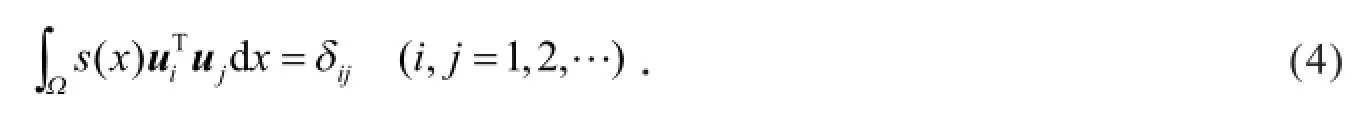
由式(2)和式(4)得

根据分部积分得

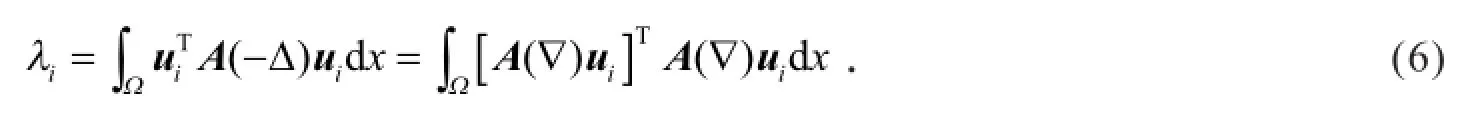
假设

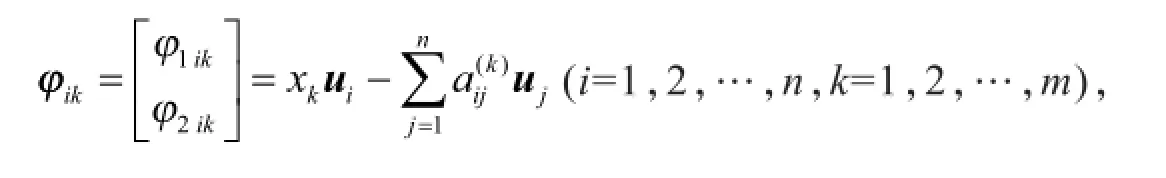
式中：

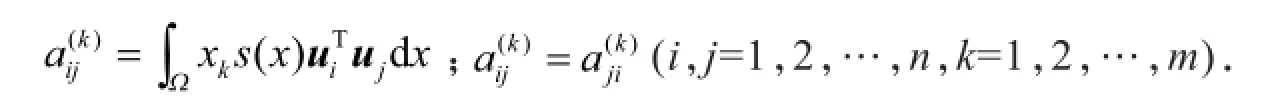
显然，φik与uj带权s(x)正交(i，j=1，2，…，n，k=1，2，…，m)，且满足

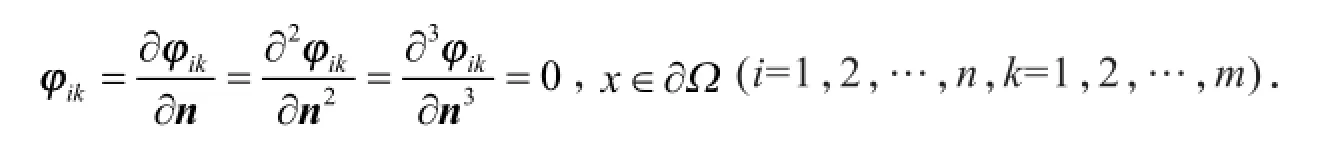
根据Rayleigh定理，得到如下不等式

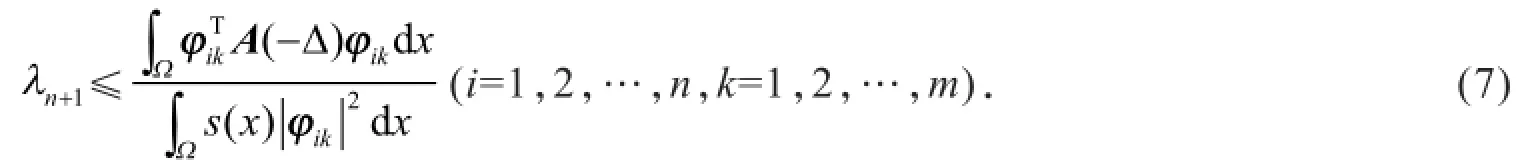
计算得

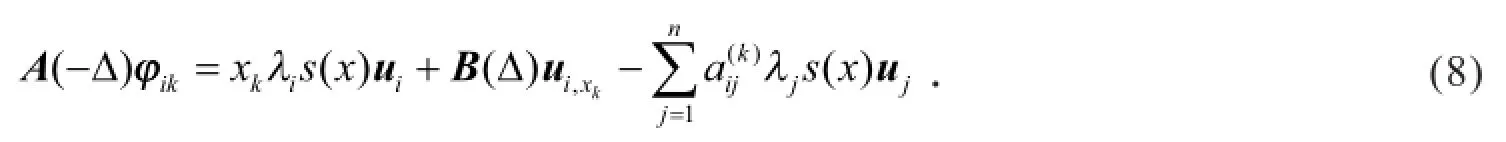
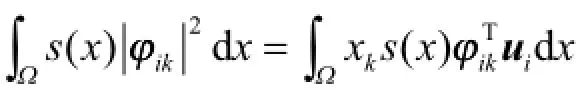
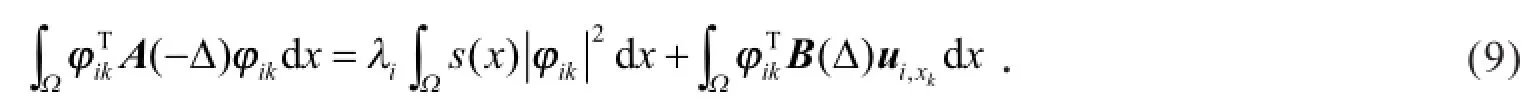
假设

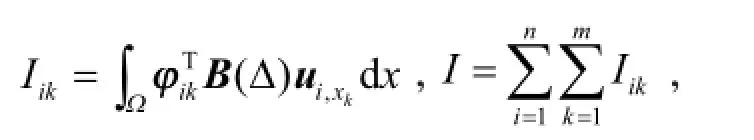
由式(9)得

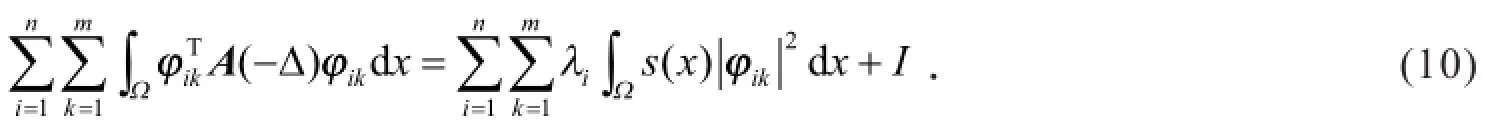
根据式(7)和式(10)有

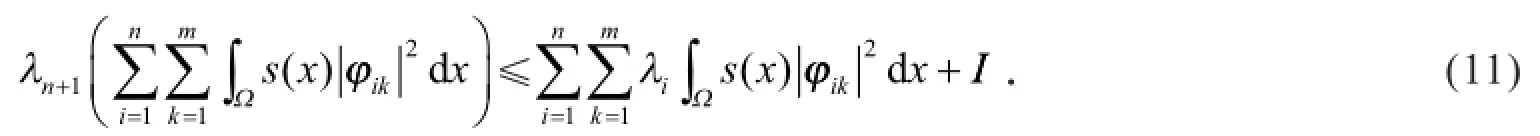
1 引理

引理1 设ui是问题(3)对应特征值的特征向量，则

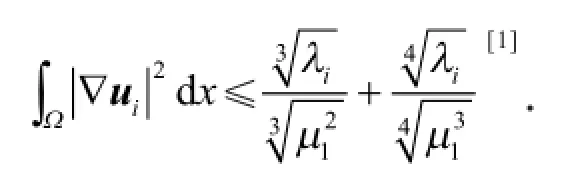
证明 根据分部积分、Schwartz不等式、式(5)和式(6)得

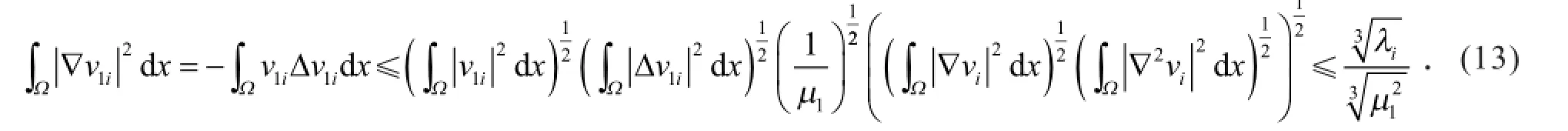
同理可得

由式(13)和式(14)得

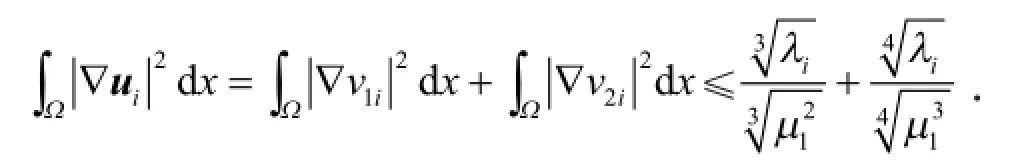
引理2 设λ1，λ2，…，λn是问题(3)的n个特征值，则

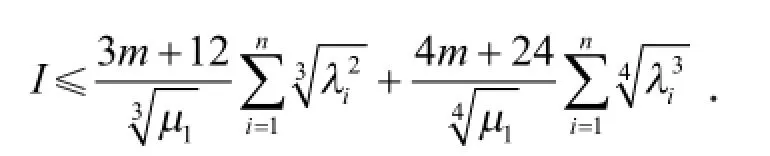
证明 由恒等式和分部积分法得

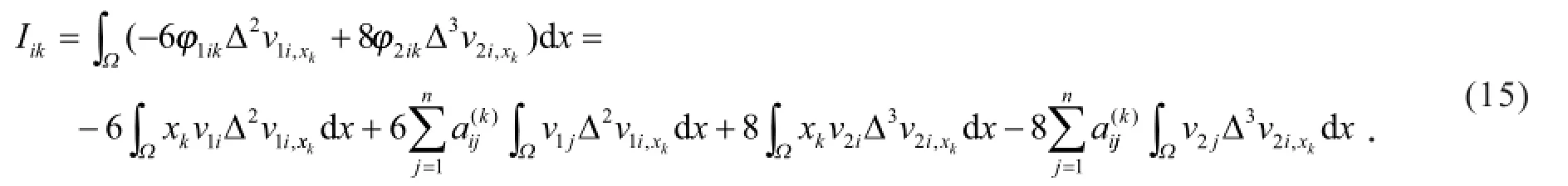
由式(15)有

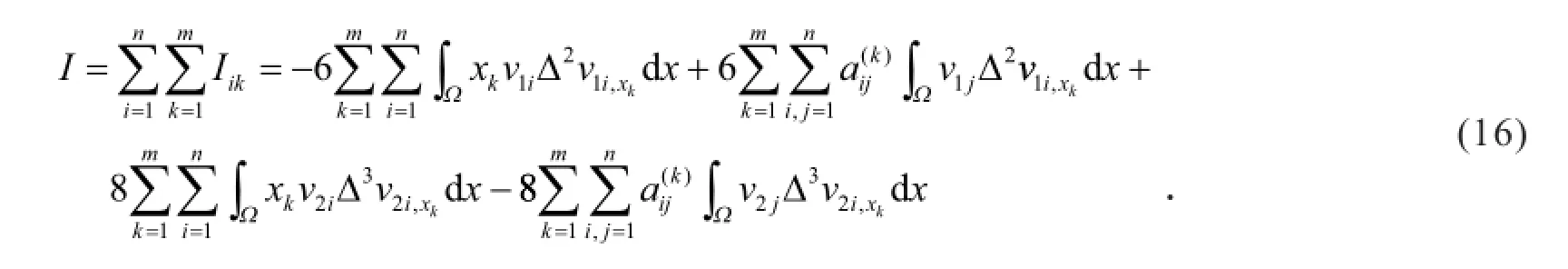
因为

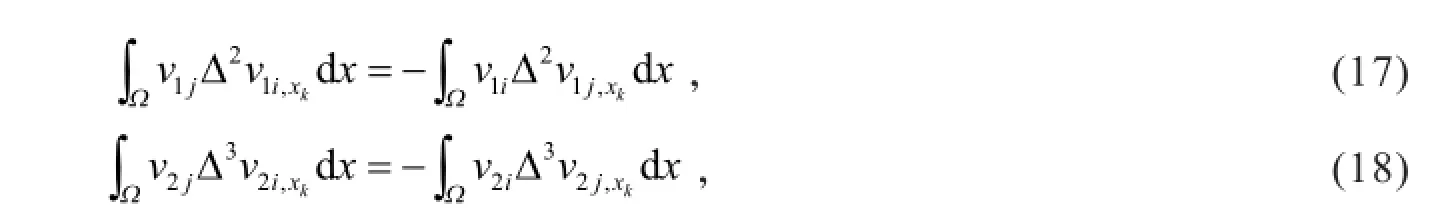
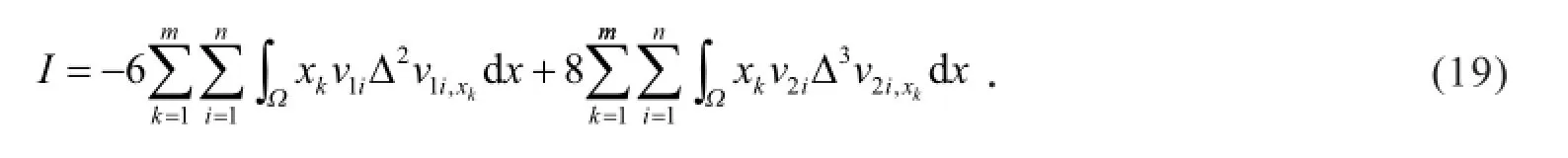
由分部积分得

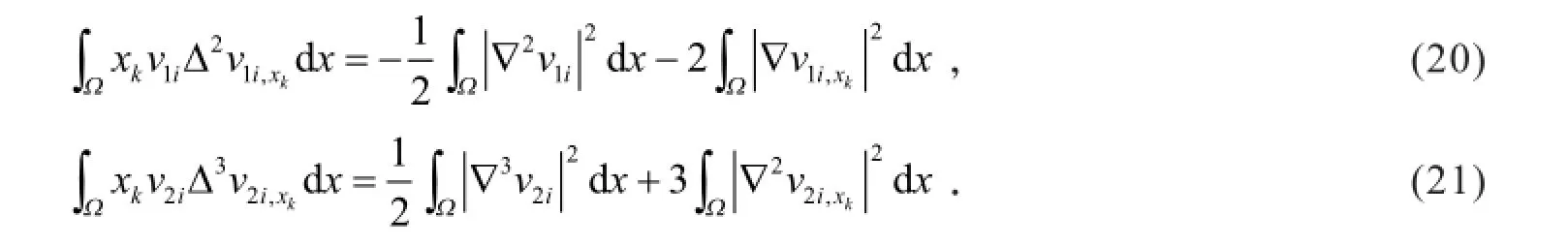
根据式(19)、式(20)、式(21)、式(5)和分部积分，有

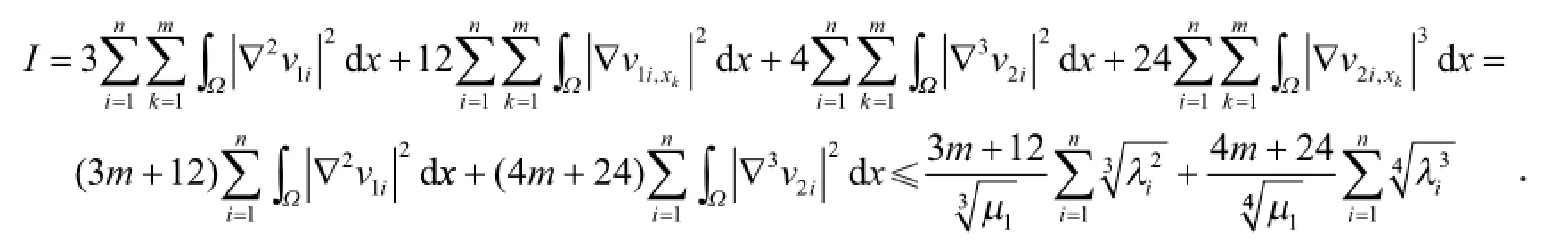
引理3 对于φik和λi(i=1，2，…，n，k=1，2，…，m)，有

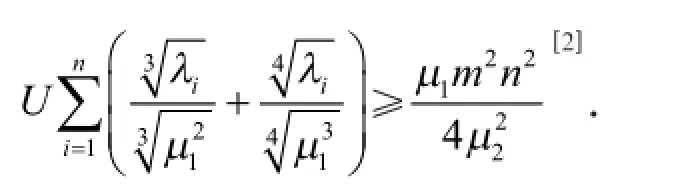
证明 根据φik的定义，有

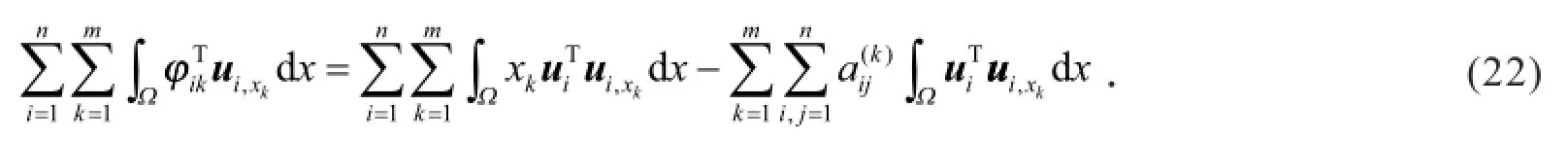
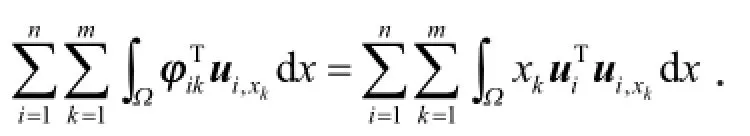
显然

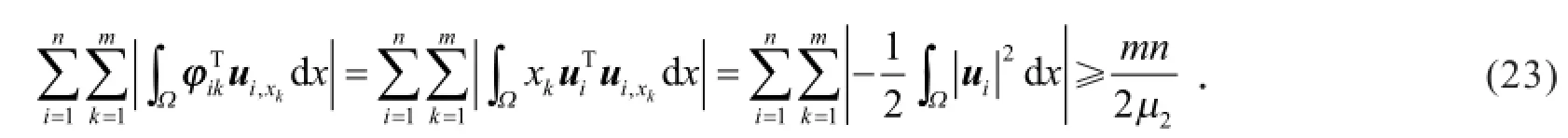
根据Schwartz不等式和引理1有

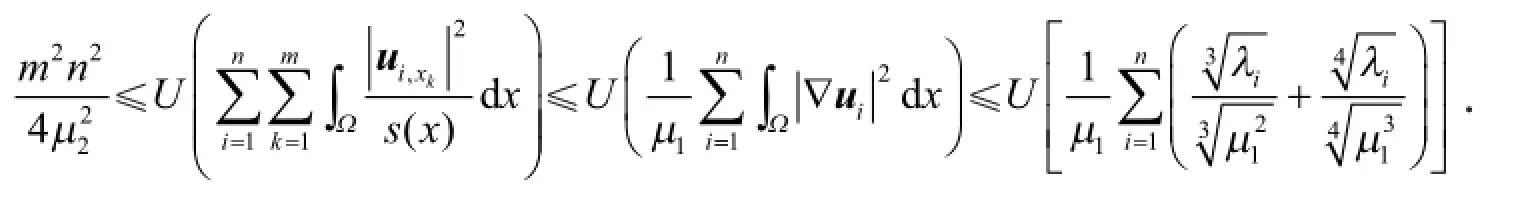
2 主要结果

定理1 若λi(i=1，2，…，n+1)是问题(3)的特征值，则

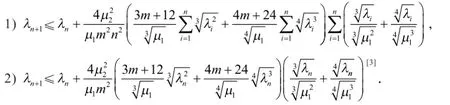
证明 根据引理3、式(12)和引理2，可得定理1的1)，在定理1的1)式右端用λn代换λi，可得定理1的2).

定理2 当n≥1，则有

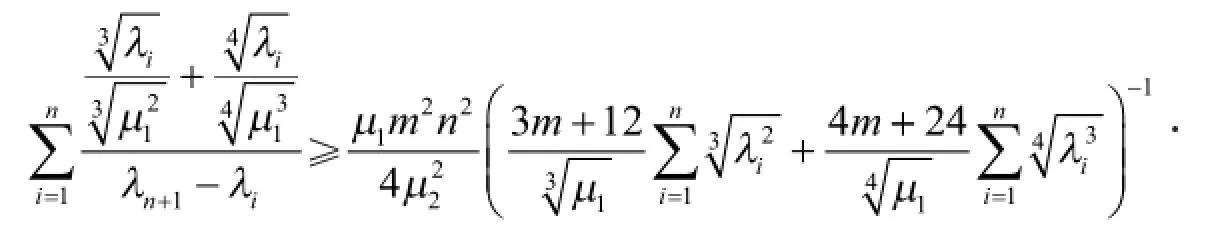
证明 设参数σ>λn，由式(11)得

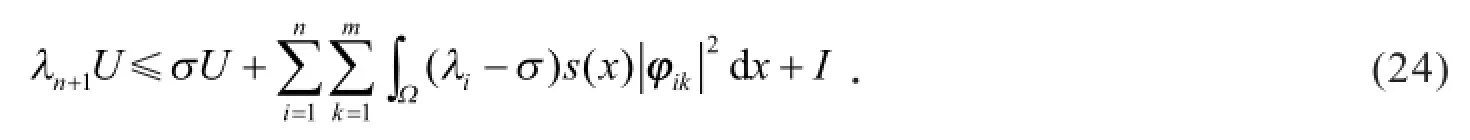
根据式(23)和Young不等式得

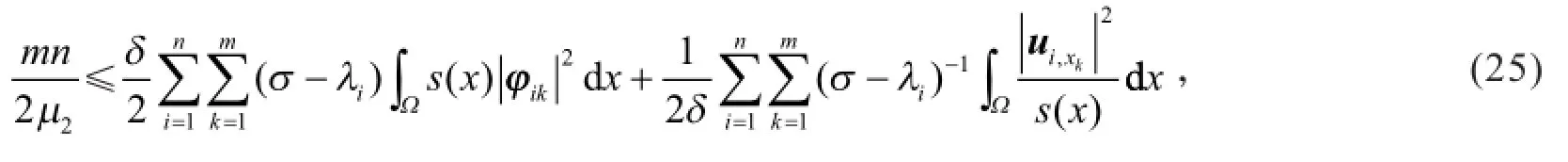
其中δ>0为待定常数.

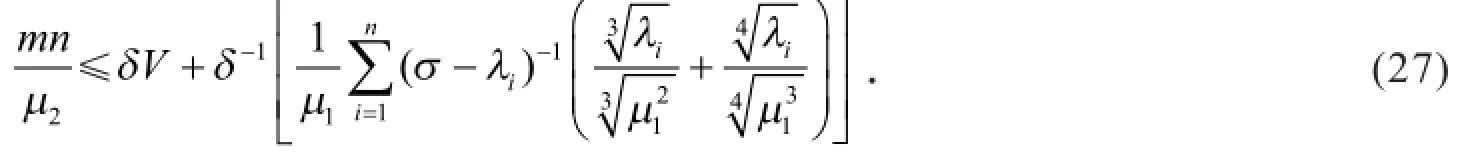
为了使式(27)式右端的值达到最小，取

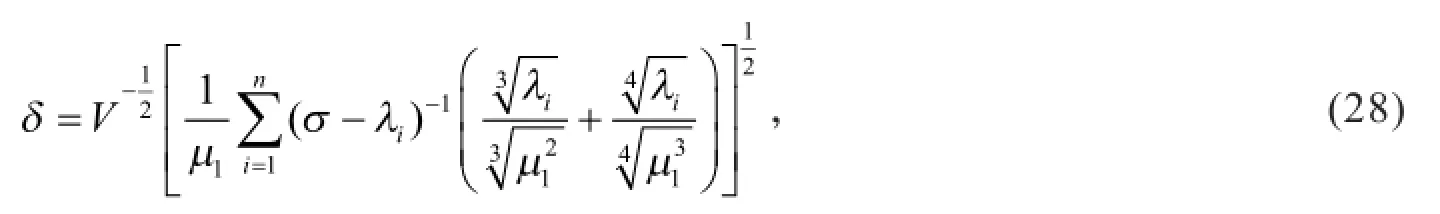
将式(28)代入式(27)有

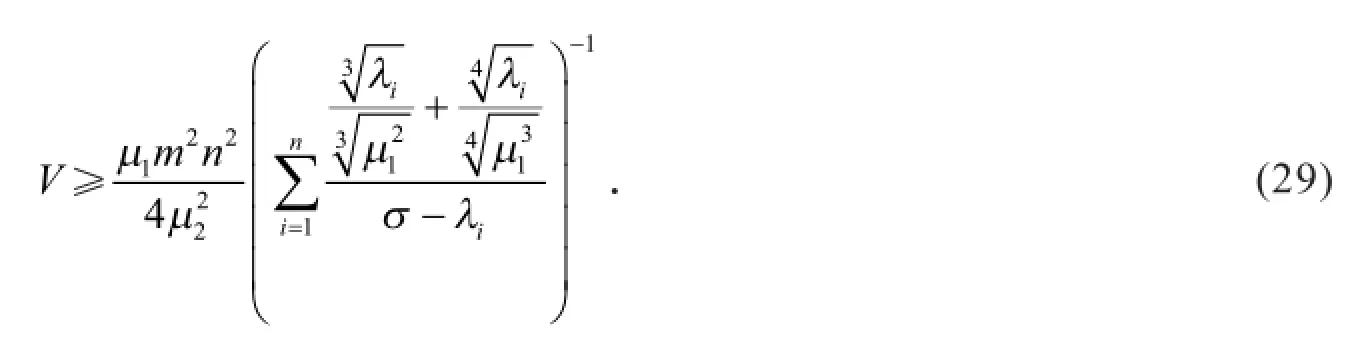
根据引理2、式(26)和式(29)得

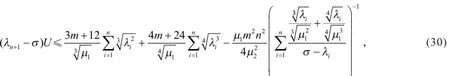
其中σ>λn，选择σ使式(30)右端等于0，即

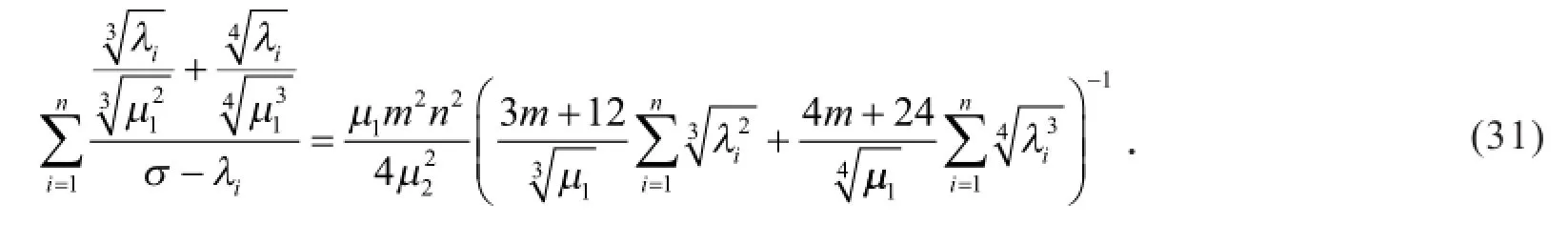
假设

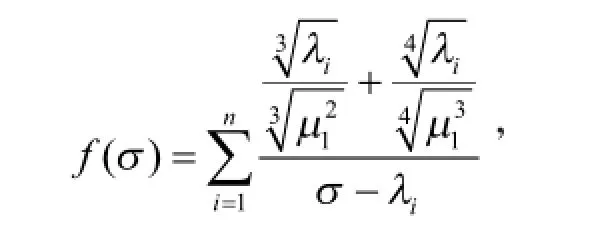
可得，函数f(σ)在(λn，+∞)内单调减少且连续，其值域为(0，+∞)，所以，存在唯一的σ使式(31)成立.由式(30)知σ≥λn+1，用λn+1来代替式(31)中σ，即得定理2.

3 结论

根据Rayleigh定理、分部积分和不等式估计等方法，得到了系统谱(特征值)的上界的不等式，其结果在数学、物理和力学等学科中有着广泛的理论研究和应用价值.

参考文献：

[1] 吴平. 一类偏微分方程特征值的上界估计[J]. 宁波职业技术学院学报，2012，16(2)：36-39.

[2] 吴平. 某类系统特征值的带权估计[J]. 商丘职业技术学院学报，2012，11(5)：27-30.

[3] 吴平. 一类偏微分系统谱的上界估计[J]. 宁波职业技术学院学报，2014，18(1)：94-97.

(责任编辑：沈凤英)

引文格式： 吴平.某类系统谱的上界[J].苏州市职业大学学报，2016，27(2)：56-60.

中图分类号：O175.9

文献标志码：A

文章编号：1008-5475(2016)02-0056-05

DOI：10.16219/j.cnki.szxbzk.2016.02.014

收稿日期：2015-12-08；修回日期：2016-01-07

作者简介：吴 平(1962-)，男，江苏苏州人，副教授，主要从事方程的特征值研究.

Upper Bound for Spectrum of A System

WU Ping
(Department of Mathematics and Physics，Suzhou Vocational University，Suzhou 215104，China)

Abstract：This paper considers estimates for spectrum of a system. The inequality of the upper bound of the spectrum is obtained by using integral， Reyleigh theorem and inequality estimation. The result is widely used in maths physics and mechanics.

Key words：a system；spectrum；upper bound；inequality