矩阵“打洞”法及其应用

赵晓苏，钱椿林(苏州市职业大学 数理部，江苏 苏州 215104)



矩阵“打洞”法及其应用

赵晓苏，钱椿林
(苏州市职业大学 数理部，江苏 苏州 215104)

摘 要：将矩阵的初等变换推广到对分块矩阵施行初等变换，华罗庚教授形象地称此方法为矩阵“打洞”.矩阵“打洞”法在矩阵计算和证明中起着重要的作用.举例说明矩阵“打洞”法在计算行列式和矩阵求逆中的应用.

关键词：矩阵“打洞”法；分块矩阵；初等变换；行列式；求逆

在线性代数中矩阵的初等变换发挥着重要的作用，例如矩阵的求逆、求矩阵的秩、行列式的计算和线性方程组的求解等，都要用到矩阵的初等变换.本文给出一个定理，将矩阵的初等变换推广到对分块矩阵施行初等变换，并且说明其方法在行列式计算和矩阵求逆中的应用.

定理 设A是m阶可逆矩阵，B，C和D分别是m×p，n×m和n×p矩阵.则有

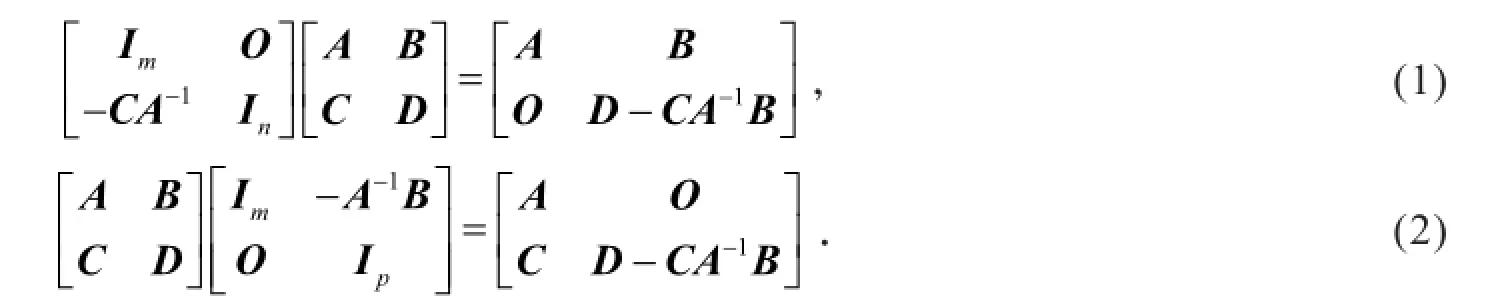
证明 直接利用分块矩阵的乘法加以验证.

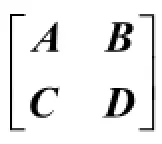
1 矩阵“打洞”法在计算行列式中的应用

证明 利用式(1)得

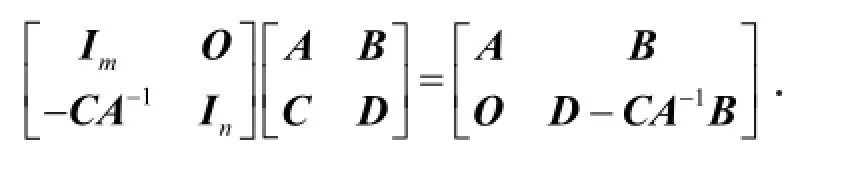
利用例1的结论，当计算高阶行列式时，可以化为较低阶行列式的计算.

解 对于三阶行列式可以化为二阶行列式的计算.

解 对于四阶行列式可以化为二阶行列式的计算.

解 对于五阶行列式可以化为二阶行列式和三阶行列式的计算.

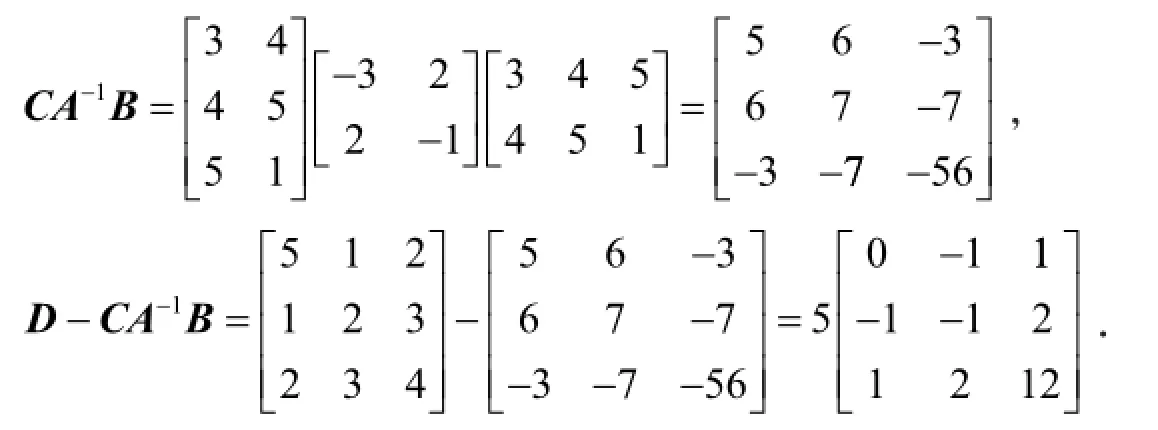
证明 利用式(3)、AC=CA和矩阵的行列式的性质，得

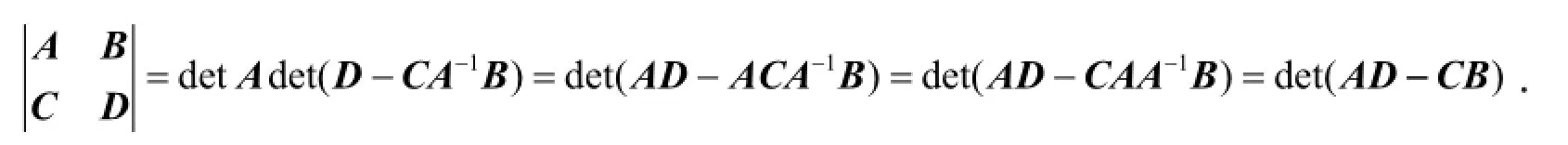
2 矩阵“打洞”法在矩阵求逆中的应用

利用式(1)得

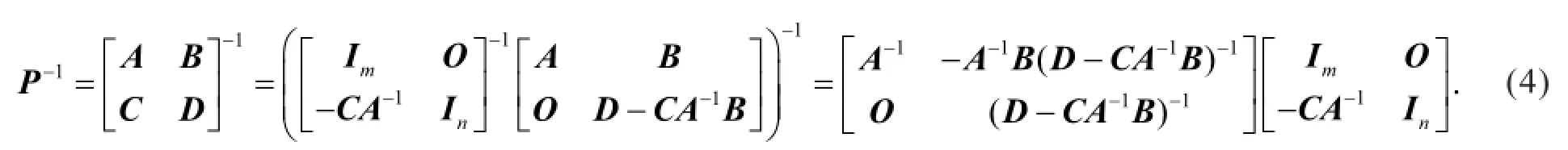
利用式(2)得

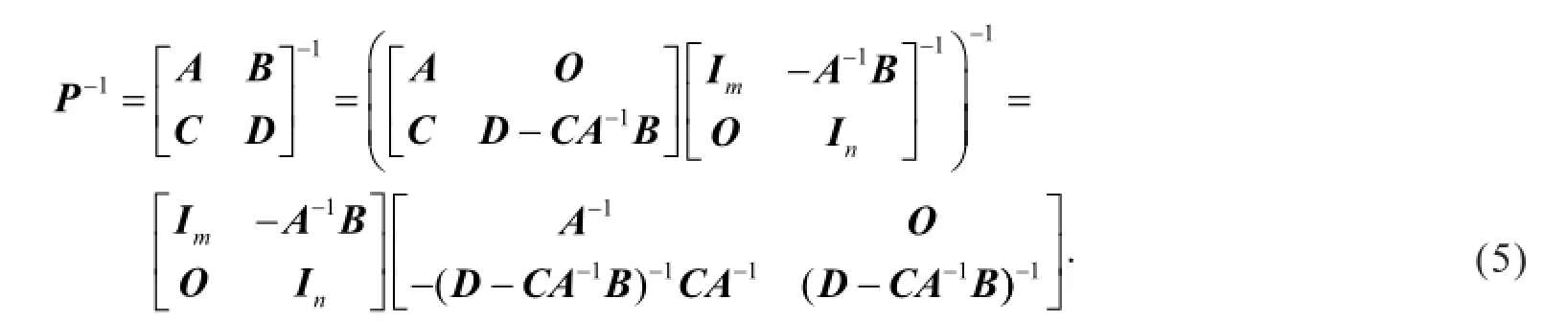
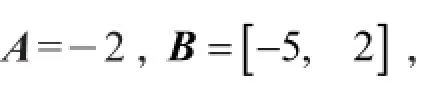
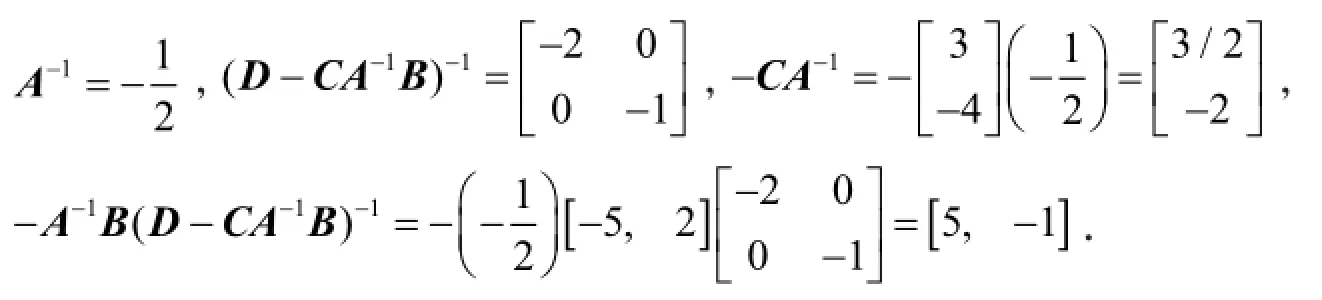
所以

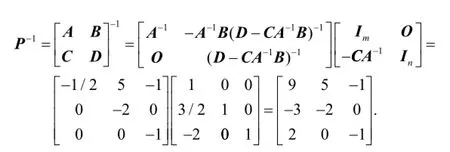
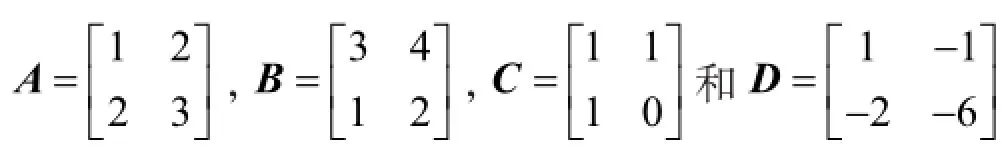
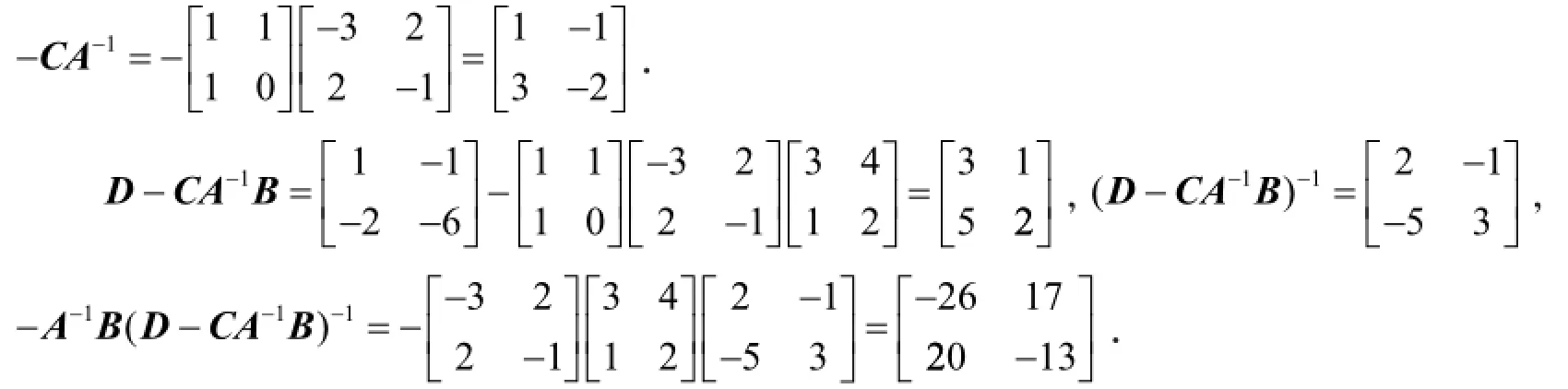
所以

参考文献:

[1] 徐利治. 大学数学解题法诠释[M]. 4版.合肥：安徽教育出版社，1999.

[2] 同济大学应用数学系. 高等数学[M]. 5版.北京：高等教育出版社，2004.

[3] 《现代应用数学手册》编委会. 现代应用分析卷[M]. 北京：清华大学出版社，1998.

[4] 《数学手册》编写组. 数学手册[M].北京：高等教育出版社，1984.

[5] 钱椿林. 线性代数[M]. 4版.北京：高等教育出版社，2014.

[6] 魏凤英. 基于矩阵求逆谈高等代数中的计算及MATLAB实现[J]. 长春大学学报：自然科学版，2013，23(10)：1277-1278.

[7] 钱椿林. 高等数学[M]. 4版.北京：电子工业出版社，2015.

(责任编辑：沈凤英)

引文格式： 赵晓苏，钱椿林.矩阵“打洞”法及其应用[J].苏州市职业大学学报，2016，27(2)：61-64，73.

中图分类号：O151

文献标志码：A

文章编号：1008-5475(2016)02-0061-04

DOI：10.16219/j.cnki.szxbzk.2016.02.015

收稿日期：2016-03-02；修回日期：2016-04-01

作者简介：赵晓苏(1962-)，女，江苏苏州人，副教授，主要从事算子特征值估计研究.

The Holed Matrix Method and Its Application

ZHAO Xiao-su，QIAN Chun-lin
(Department of Mathematics and Physics，Suzhou Vocational University，Suzhou 215104，China)

Abstract：This paper addresses the elementary transformation of matrix extension to elementary transformation of block matrix， which Professor Hua Luogeng described vividly as the holed matrix. The holed matrix method plays an important role in the proof of matrix and the calculation of the matrix. This paper illustrates the application of this method to the calculation of the determinant and inverse matrix.

Key words：the holed matrix method；block matrix；elementary transformation；determinant；inverse