高职院校目标绩效考核的数学模型研究
2016-05-26宋艳丽
宋 武, 宋艳丽
(黄冈职业技术学院,湖北 黄冈 438002)
高职院校目标绩效考核的数学模型研究
宋武, 宋艳丽
(黄冈职业技术学院,湖北 黄冈 438002)
摘要:高职院校目标绩效考核中,各部门的不同任务分值权重的设置和考核分值计算的合理性是衡量考核结果有效的关键因素。对各任务权重设置数学模型和考核分数计算数学模型的研究,指导高职院校合理设置目标任务分值权重,以及相关考核部门和人员给予有效评分,从而做到通过目标绩效考核调动教职工工作积极性,促进学校教育教学改革,提高人才培养质量。
关键词:权重;层次分析法;数学模型
当前,高职院校为了不断深化教育教学改革,调动广大员工工作积极性,开展了年度目标绩效考核。那如何分配好每个部门每项任务分值的权重,年末如何有效的给各部门考核,将直接影响到开展目标绩效考核的初衷。通过调查,现在不同高职院校在目标绩效考核中,存在考核指标分值权重随意设置、考核者随意打分等问题,针对上述问题提出了目标绩效考核任务分值权重设置的数学模型和年度考核的数学模型。
1模型建立的思路
1.1目标任务分值权重设置
考核任务权重的模型,采取了层次分析法来进行设置。层次分析法(AHP)是由美国运筹学家T.L.saaty于20世纪70年代提出来的,是一种解决多目标复杂问题的定性与定量相结合的决策分析方法,它是用决策者的经验来判断各衡量目标能否实现标准之间的相对重要程度,并合理地给出每个决策方案的各标准的权数,利用权数求出各方案的优劣次序[1]。应用这种方法,决策者通过将复杂问题分解为若干层次和若干因素,在各因素之间进行简单的比较和计算,就可以得出权重。AHP法的设计步骤是首先要把问题层次化,再构成一个多层次的分析结构模型,相对于最高层(总目标)的重要性权值的确定或优劣次序的排序问题,从而确定各项具体任务的权重[2]。
1.2考核任务分值计算
考核分值的模型建立,主要关注的是目标任务是谁考核,怎么考核的问题。高职院校年度目标绩效考核的结果一般有过程性考核和阶段性考核两种情况。过程性考核,考核结果要分周、分月统计并通报考核情况,过程性考核可以根据等次量化成分数,避免因考核分数拉开差距或者分数区别很小。阶段性考核一般可分为期中和期末两个阶段,在进行阶段性考核时,考核通过考核小组,设置打分区间,考核者保证各等次中具有一定的比例。
2数学模型的建立与应用
2.1目标任务分值权重的数学模型
目标绩效考核中确定考核指标权重是一个复杂的系统工程,由于各高职院校的职能划分不同,各部门的职责不同,工作性质不同,很难用统一的标准来为各项任务设置权重,下面对权重的设置分为两大类,对教学单位而言,工作职能基本相同,可以采取同一的指标体系,如教学常规管理、教学基本建设、师资队伍建设、科研与社会服务、学生教育与管理以及其他共性指标(综合治理、计划生育、信息化建设、宣传、档案管理、资产管理、经费管理)。对非教学单位而言,职能部门不同,工作的职责也不同,此处可分为量化指标、定性指标以及共性指标。那么如何确定各类考核的权重,是一个非常关键性的问题[3]。下面我们以教学单位目标任务权重的设置为例,来介绍AHP法权重设置步骤。
一是建立层次结构图。对高职院校的教学单位而言,选取了学生教育与管理、教学常规管理、师资队伍建设、科研与社会服务、教学基本建设作为完成教学单位任务的主要指标(其他相关工作可以融合到这五个指标之中)。层次结构图如图1所示。

图1 高等学校教学单位的目标与任务层次图
二是建立两两比较的判断矩阵。判断矩阵表示针对上一层次某单元(元素),本层次与它有关单元之间相对重要性的比较。在层次分析法中,为了使判断定量化,关键在于设法使任意两个任务层对于目标层而言相对优越程度得到定量描述,层次分析法采用1-9标度方法,对不同情况的评比给出数量标度,为了让被调查者容易选择,我们只采取了 5 个标度,即 2 个因素相比: 同等重要、前者比后者稍重要、前者比后者重要、前者比后者很重要、前者比后者极重要。具体比较量化数值如表1所示。

表1 判断矩阵元素aij的标度方法表
通过选取各教学单位和相关职能部门的主要领导、部分专业负责人和专业教师代表组成评判团,得出了如下比较判断矩阵Pij。
此判断矩阵具有如下特征:Pii= 1; Pji= 1/ Pij;Pij= Pik/Pj k(i,j,k=1,2,….n)。
三是对判断矩阵Pij进行一致性检验。计算一致性指标CI公式。
一致性指标CI的值越大,表明判断矩阵偏离完全一致性的程度越大, CI的值越小,明判断矩阵越接近于完全一致性。一般判断矩阵的阶数n越大,人为造成的偏离完全一致性指标CI的值便越大;n越小,人为造成的偏离完全一致性指标CI的值便越小。对于多阶判断矩阵,引入平均随机一致性指标 RI,T.L.saaty通过正互反矩阵计算1000次得到了1-9阶的平均随机一致性指标,阶数与一致性指标对照表如表2所示。

表2 T.L.saaty得出的阶数与一致性指标对照表
判断矩阵一致性指标 CI与同阶平均随机一致性指标RI 之比称为随机一致性比率CR。
当 CR<0.10时,便认为判断矩阵具有可以接受的一致性。当CR ≥0.10时,需要调整和修正判断矩阵,使其满足CR<0.10,从而具有满意的一致性。
通过计算判断矩阵Pij最大特征根λmax=5.073。
得到的权向量:w =(0.263,0.475,0.055, 0.090,0.110)T
利用公式可以得到一致性指标CI为:
随机一致性指标 RI=1.12 (查表)。即一致性比率CR=0.018/1.12=0.016<0.1通过一致性检验。从而得到了教学单位各项考核任务的权重。非教学单位考核任务权重要根据各部门的工作职责来衡量,计算方法可以仿照教学单位权重设定方法。
2.2考核任务分值计算的数学模型
1.多人测评同一指标
需要多人来同时测量同一指标时,如职能部门的服务测评,需要全体教师或教师代表对服务测评这个指标进行评价,人数越多,评价的尺度越难以统一,这种情况可以采取评价“优”、“良”、“中”的方式,通过统计“优”、“良”、“中”的个数,再折合成对应的分数。“优”、“良”、“中”分别对应多少分数,可以采取随机调研方式,或者对不同学校的近几年的测评情况进行分析,得到衡量的权重。计算公式如下:
假设评价的人数为N,评价的部门为M。其中Mi表示第i部门的得分,对第i部门的评分情况如下,评价“优(Y)”有a人,评价“良(L)”有b人,评价“中(Z)”有c人。其中a+b+c=N,则第i个部门的分数为:
Y、L、Z各代表多少数值,可以根据学校的实际情况来确定,如设某学校根据历年测评情况,确定了“优”为95分、“良”为90分、“中”为85分。
则第i个部门的分数为:
2.多人测评不同部门不同指标
机关职能部门工作职能不同,每个部门工作任务不具有可以比性,对机关职能部门的考核时,一般在校领导带队情况下,从各教学单位中抽取一定数量的考评人员,由考评人员结合目标任务的完成情况依次打分。这种情况下,要对考评人员设置打分区间,汇总分数时,除掉一个最高分和一个最低分,其余求平均值。设考核人员有n(n≥5)人,其中ni表示第i人对某个部门Mj所打的分数,注意在打分中要设置优秀、良好和中等的打分区间。这类情况考核分数数学模型如下:
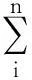
3.一人(部门)测评不同部门同一指标
这种评价,主要是机关职能部门针对教学单位某项具体任务的考核,比如教学常规管理一般由教务处组织考核,学生管理工作一般由学生工作处组织考核,还有档案管理工作一般由学校办公室来组织考核。从以上三个具体的任务来看,显然档案管理工作一般一年才组织1-2次,档案管理工作是要去查看现场,由学校办公室直接考核显然不太公平,可以采取由各部门的档案管理员组成考评队伍,对各部门进行考核,这样一来,各个档案管理员可以互相学习,也提高了考核的公平和工作性,考核分数的计算方法可以参考多人测评不同部门不同指标的计算方式,求平均值;而教学常规管理和学生管理属于过程性考核,一般学校每周或每月就要公布一次考核结果。对应过程性考核,采取每周或每月排名的形式,再将排名的结果进行量化处理,年末将每周量化的分值求平均值。如学生工作处第i周对A、B、C、D、E、F、G七个部门的指标(到堂率、旷寝率)所测评的情况依次为Ai、Bi、Ci、Di、Ei、Fi、Gi,其大小关系假设为:Ai〉Bi〉Ci〉Di〉Ei〉Fi〉Gi。
比较大小关系后,再将其量化处理为对应的分数,假如每个等次间相差2分。则可以将A、B、C、D、E、F、G七个部门量化成分数100、98、96、94、92、90、88。
设这一年有w周,则A部门本年度的得分Fa为:
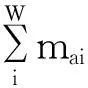
年末各部门考核的分数是学校对各部门一年来工作完成情况的检验,考核公平公正,能有效激励大家改进工作方式,提高工作效率。以上介绍了目标任务权重的设置方法和考核分值确定方法,年终分数由各职能部门考核的结果(按百分制计算)与权重的成绩,再将所有任务的分数叠加即可。
以上介绍了考核权重的设置和考核分值的确定的数学模型,各高职院校可以根据学校的实际情况,对上述计算方式进行选取。
参考文献:
[1]王友青,裴成荣.AHP——绩效考核指标权重系数确定的有效方法[J].重庆职业技术学院学报,2005(1): 90-91.
[2]王薇.KPI绩效考核权重设计方法探析[J].时代金融,2014(21):194-195.
[3]张文祥,赵辉.重构大学院系和职能部门工作绩效考核体系的思考[J].煤炭高等教育,2004(6):38-40.
[责任编辑:张克新]
DOI:10.3969/j.issn.1672-1047.2016.02.28
中图分类号:O141.4
文献标识码:A
文章编号:1672-1047(2016)02-0097-03
作者简介:宋武,男,湖北监利人,讲师,工程硕士。研究方向:数据分析与目标管理。
基金项目:湖北省教育科学规划研究课题“高职院校目标绩效考核创新与实践”(2015GB264)。
* 收稿日期:2016-03-12
