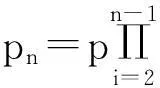一道概率竞赛题的解法思考

江苏省海门市海门中学　(226100)　樊陈卫



一道概率竞赛题的解法思考

江苏省海门市海门中学(226100)樊陈卫

2014年高中数学联赛第8题：

解法1：4个点之间可以连6条线，每条线有连与不连两种情形，共有26种不同情形，考虑其中可以用折线连接AB的情况有：

(1)有AB边：共25种情况;

(2)无AB边，但有CD边.此时AB可用折线连接即为A与CD之一连接且B与CD之一连接，共有(22-1)·(22-1)=9;

(3)无AB边且无CD边.此时AC、CB相连有22种情况，AD、DB相连有22种情况， 但其中AC、CB、AD、DB均相连被重复计算了一次，故共有22+22-1=7.

分析2：能否用概率性质来思考这个问题.“ A、B可用(一条边或若干条边组成)空间折线连接”看成是“经过AB边相连”与“经过C或D相连”两个事件的和，两个事件独立但并不互斥，如图1“经过C或D相连”，若CD不相连，则ACD与ABD两种独立但不互斥的情况；若CD相连，则可把CD理解为一点，“经过C或D相连”即为A—CD—B，也即“A与CD相连”且“B与CD”相连.

两种方法比较，法1把问题转化为计数问题，直观形象，比较容易想到但容易遗漏重复.法2从概率的性质角度考虑问题，具有一般性，但事件之间关系不易厘清.法2的优势在于可以解决问题的一般化推广：“设ABCD是空间4个不共面的点，以p的概率在每对点之间连一条边，任意两点之间是否连边相互独立，求A、B可用(一条边或若干条边组成)空间折线连接的概率.”有兴趣的读者不妨一试.

对这个问题一般化，可得到如下问题：设空间n个不共面的点，以p的概率在每对点之间连一条边，任意两点之间是否连边相互独立，则任意两点可用(一条边或若干条边组成)空间折线连接的概率为.