以线段长为最值的试题的解法探究

浙江省临海市东塍镇中学　(317000)　潘优红



以线段长为最值的试题的解法探究

浙江省临海市东塍镇中学(317000)潘优红

实行新课程标准以来，各地中考以线段长最大(或小)值为载体的新编试题频频出现，在我们的日常教学中也常遇到此类问题.从我们的教学实践中知道，学生对这类问题很不适应，往往难以入手，理不清解题思路，面对选择题、填空题时，仅凭直觉去猜答案.其实，解这类问题的根本依据往往又是学生很熟悉的性质：两点之间线段最短.或是另一种表达形式：三角形两边之和大于第三边(或两边之差小于第三边).学生往往忽略这一基本性质，或由于题目条件的隐蔽而找不到与这一性质的联系造成思维受阻.“人教2013年版《义务教育课程标准实验教科书·数学》八年级上册”第85页13.4课题学习《最短路径问题》中的问题一(饮马问题)与问题二(造桥选址问题)，提供了我们解这类问题的两个很好的模型.下面我们对一些试题的解法根据教学实践作一些整理与探究，供同行研讨，供同学参考.

一、应用“饮马问题”模型解题

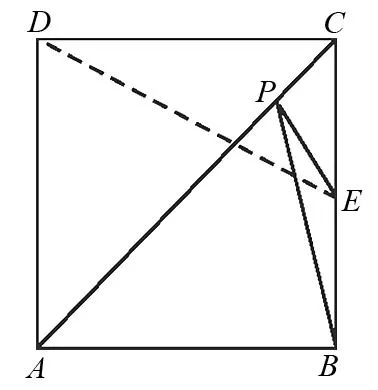
图1

题1(2012年攀枝花中考题)如图1，在正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为.

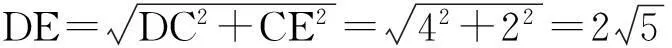
题2(2012年滨州中考题)如图2，在平面直角坐标系中，抛物线y=ax2+bx+c经过A(-2，-4)，O(0，0)，B(2,0)三点.

(1)求抛物线y=ax2+bx+c的解析式；

(2)若点M是抛物线对称轴上一点，求AM+OM的最小值.

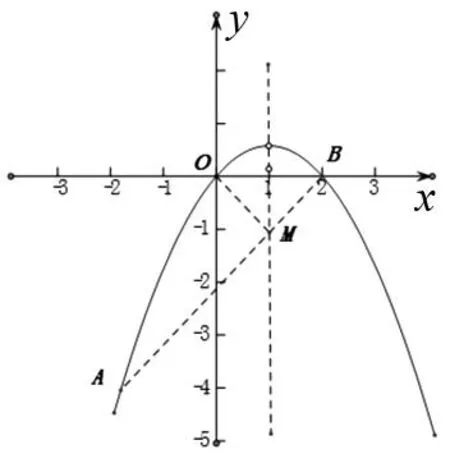
图2

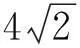
二、应用“造桥选址问题”模型解题

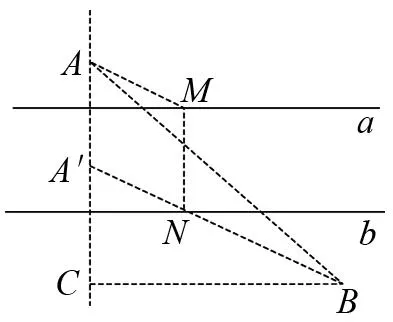
图3

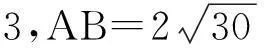
(A)6(B)8(C)10(D)12

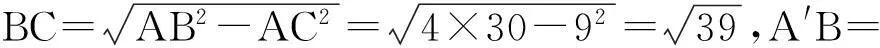
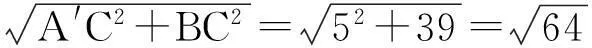
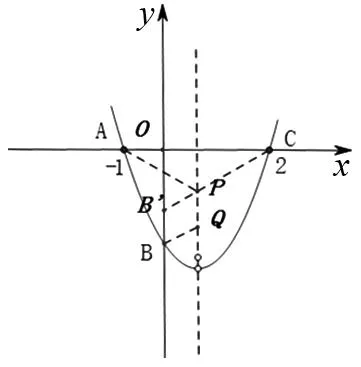
图4

(1)求A、B、C三点的坐标；

(2)已知点D在坐标平面内，ΔABD是顶角为120°的等腰三角形，求点D的坐标；

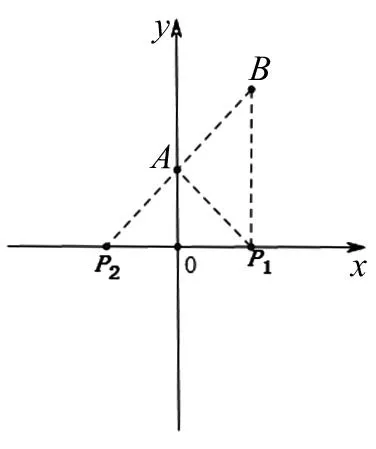
图5

三、其他涉及线段长最值问题

题5在平面直角坐标系xoy中，已知A(0，1),B(1，2 ).点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是.

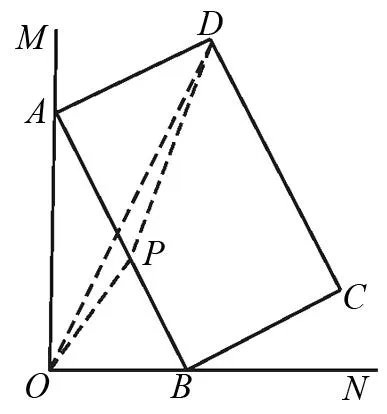
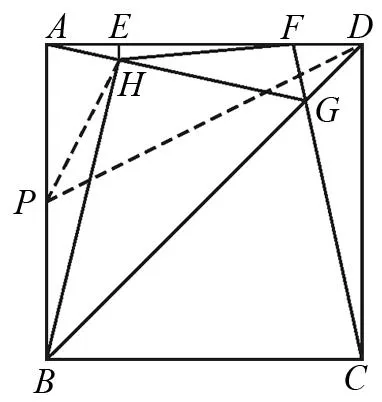
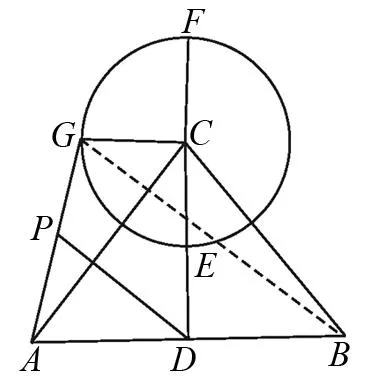
解法探究：解这类没图的题，首先要画出示意图，以直观的形式提供我们解题思路.于是画如图5，再表述出点P到A、B两点距离之差的绝对值|PB-PA|.怎样找它的最大值呢？我们联想到三角形两边之差小于第三边，则有PB-PA

图6

图7

题7(2012年济南中考题)如图7，∠MON=90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为().

图8

题8(2013年武汉中考题)如图8，E,F是正方形ABCD的边AD上两个动点，满足AE=DF，连接CF交BD于点G，连接BE交AG于点H，若正方形的边长为2，则线段DH长度的最小值是.

解法探究：本题图形比较复杂，DH的长似乎无规律可循.我们只好重新阅读题目，从中找出隐含的条件.正方形隐含的边相等、角相等且都是直角、关于直线BD对称.现在这些对我们有用吗？结合图形及AE=DF，可得△ABE≅△DCF、△ADG≅△CDG，所以 ∠ABE=∠DCF=∠DAG，这时可以证明∠AHB=90°

图9

题9(2015年杭州江干区中考模拟题)如图9,CA=CB，AB=6，CD=4，E是高线CD的中点，以CE为半径作⊙C，G是⊙C上一个动点，P是AG中点，则DP的最大值为().