数学文化的课堂渗透例析

江苏省常熟市中学　(215500)　吴旭红



数学文化的课堂渗透例析

江苏省常熟市中学(215500)吴旭红

著名数学家柯朗在名著《数学是什么》的序言中写道：“教师学生和一般受过教育的人都要求有一个建设性的改造，其目的是要真正理解数学是一个有机整体，是科学思考与行动的基础．”

笔者有幸于2015年12月30日，在张家港沙洲中学开展的苏州名师共同体高中数学I组研修活动中，向孙卫星，平卫星两位老师学习了同课异构——解析几何中的定点、定值问题，对于数学文化和数学文化在课堂教学中的渗透有了崭新的认识和体会．

课堂实录一(张家港沙洲中学孙卫星)

引例(苏教版数学选修2-1第42页习题2.3第5题改编) 在ΔABC中，B(-2，0),C(2，0),直线AB，AC的斜率乘积为-1，顶点A的轨迹方程是.

学生思考后师提问．生1：几何法(垂直得圆)．生2：用坐标运算，化简得x2+y2=4(y≠0)．师引导学生尝试变化乘积值，猜测结果．生3：k1·k2=-2，师请学生一起猜想？生一致认为是椭圆．方程呢？引出用代数解决几何问题，体会解析几何本质．

师要求变式：直线AB，AC的斜率乘积为m，讨论动点A的轨迹．

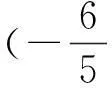
课堂实录二 (常熟市中学平卫星)

直入课题：同学们，我们已经学完了圆锥曲线，那是跟圆一样优美对称的图形，今天我们一起研究“解析几何中的定点定值问题”．

学生活动1 (苏教版数学选修2-1第42页习题2.3第5题改编)若A为圆x2+y2=R2(R>0)上任一点，M,N是圆上关于圆心对称的两点，当直线AM,AN的斜率都存在时，kAM·kAN是否为定值？若是，定值为多少？

生1：根据直径所对圆周角为90°，得kAM·kAN=-1.

师给出结果，请学生课后研究．

这是两堂注重数学文化渗透和培养的示范课，让人回味无穷．

下面从三个方面来进行分析．

一、数学文化促开端——引人入胜

在数学上既要大胆猜想，但又不能脱离理论实践．数学追求完全确定性的知识．

两位教师都从教材上的习题出发，重视了教材文化的传承，关注教材例习题的教学价值．孙老师引导学生改变k1·k2的值，运用圆的几何性质到椭圆、双曲线，让学生体会用坐标运算精确求解的重要性．通过数据的改变，使用数学特有的工具——几何画板的演示，用运动的观点，体现了“数⟹形”的联系，渗透了“特殊到一般”的数学思想．学生主动探索了研究问题的方法，提高了学生学习数学的兴趣．经由圆的几何性质，指出解析几何中的定点定值问题就是变化过程存在不变量的问题．之后定义椭圆和双曲线中的“直径”来研究相关定值问题，让人耳目一新．既培养了学生的阅读理解能力，又从学生的最近发展区去研究问题的本质，隐晦地运用了类比思想．平老师亦从圆出发，然后由椭圆上特殊点探求kAM·kAN的值，推广到一般位置的点，紧抓关于原点对称这一条件．教师依据学生的表述，示范了严密的书写，体现了数学的严谨．再请学生类比到双曲线中，重视了类比的本质——方法的类比，以此结束了定值问题的探究．

二、数学文化引高潮——跌宕起伏

爱因斯坦说过：“美，本质上终究是简单性．”希尔伯特认为：“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着．”数学追求最简，需时时渗透，重在学生体验和选择．两位老师都有所得，学生亦有所得．

三、数学文化留深思——发人深省

两位老师都留了问题让学生思考，笔者也在思考．两位老师留给学生的并不仅仅是一个题目，而是对课堂的回顾和运用，对数学的思考．促使学生在学习数学过程中真正感受到文化感染，产生文化共鸣，体会数学的文化品位．教师亦然．

数学文化是指数学的思想、精神、方法、观点、语言，以及它们的形成和发展，以及数学家，数学史，数学美，数学教育，数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系，等等．在这样的非新授课教学时，教师结合教授内容把对它的理解，把握，通过课堂，培养学生用数学的观点进行观察，构建数学模型，学习数学的语言、图表、符号表示，进行数学交流．通过理性思维，培养严谨素质，追求创新精神，欣赏数学之美，体味数学的内涵．

结束语：二位老师的课堂精彩纷呈，孙老师注重学生知识生成的培养，数形结合，动中有静，思维锻炼多；平老师注重方法的获得，计算能力的培养，讲练结合，粗中有细；他们都注重了学生的已有认知水平，学生的主体地位，学生的收获，从中获得自身的幸福．

《标准》要求贯彻素质教育思想，既着眼于提高学生的数学素质，又着眼于提高学生的文化素质和思想素质．使学生了解数学的文化，理解数学的知识，深层次看待数学发展．张奠宙先生曾经说过：“优秀的数学文化，会是美丽动人的数学王后、得心应手的仆人、聪明伶俐的宠物．伴随着先进的数学文化，数学教学会变得生气勃勃、有血有肉、光彩照人．”如何让数学美充满活力，我们高中教师在课堂教学中，要与学生一起，在具体的数学概念、数学方法、数学思想中揭示数学的文化底蕴．注重知识性、趣味性、思想性、应用性的统一，注重师生互动，注重数学思维的培养，注重欣赏数学，注重享受数学，让数学课堂充满欢笑与幸福．