年年岁岁题相似,岁岁年年题不同——形散神同的几道高考解几题的研究

黑龙江省牡丹江市第八中学　(157014)　孔德泉



年年岁岁题相似,岁岁年年题不同
——形散神同的几道高考解几题的研究

黑龙江省牡丹江市第八中学(157014)孔德泉

在全国高考异彩纷呈的大舞台上,解析几何试题一直扮演着重要角色,这道综合题集数形结合、函数与方程、转化与化归等重要数学思想于一身,是甄别学生层次的较好题目,文理科均以压轴题或次压轴题出现,其地位及作用举足轻重.该试题求解常常需要学生具有较强的计算能力,涉及较大的计算量时学生常心存恐惧,望而却步,引得无数学子竞折腰,成为部分学生突破高分的一个瓶颈.

分析解析几何试题,把握解析几何复习备考方向,突破该题,取得相应分数是全体考生的期盼,更是数学教师的重要使命,高考命题专家会对具有典型背景的试题分不同年份,不同省份,不同变式进行多角度考查,正可谓,年年岁岁题相似,岁岁年年题不同.数学教师引导高三备考学生对于本质相同的解析几何问题进行拓展研究,显得尤为重要.本文通过对2009全国二卷,2013北京卷,2015全国新课标Ⅱ,2015山东解析几何综合题出自同一背景的探究,意在揭示这几道解析几何题的联系,发现高考命题的规律,有效地提高高三复习效率.

1.形散神同

2015山东理科第20题对此命题进行了考查：

(Ⅰ)求椭圆C的方程；

图1

2015全国新课标Ⅱ理科第20题正是考查此推论:已知椭圆C： 9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,直线l与C有两个交点A,B,线段AB的中点为M.

(Ⅰ)证明：直线OM的斜率与直线l的斜率的乘积为定值；

(Ⅰ)求a,b的值；

命题中的OAPB为平行四边形可否成为菱形,结论会怎样？于是得到命题3与2013北京卷解析几何题的不期而遇.

图2

(1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积；

(2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由．

由命题2及推论得,AC为x2+4y2=1的切线,由图易知OB与AC垂直,AC的斜率不存在,点B是W的顶点(证明略).

2.拓展探究

波利亚曾说：“类比是一个伟大的引路人, 类比是提出新命题或获得新发展之不竭的源泉”.在双曲线中结论如何？过原点O的射线与母双曲线,子双曲线分别交于点P,M,过子双曲线上的点M作切线与母双曲线无交点成为探究的难点,可是与其共轭双曲线交于两点,结果柳暗花明,水落石出.得到如下命题：

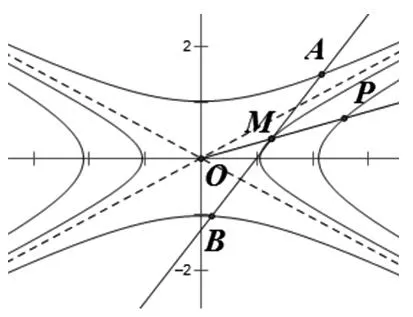
图3

通过类比同样可得双曲线的命题4的有关推论.此处留给读者继续研究.

根据以上背景分析,适当变式又可编拟许许多多的相关试题,如平行四边形成为矩形、正方形可编拟习题1、习题2,椭圆替换为双曲线可编拟习题3等.

3.复习建议

第一、各省市高考试题凝聚了命题专家的集体智慧,具有权威性、示范性、借鉴性,在解析几何知识复习时,一定要选择高考真题作为备考习题,研究同一省份近几年、近十几年,甚至更久的高考真题,不仅仅是解析几何题如此；第二、认真研究这些备考习题,不仅要和学生一起探究其共同背景,还要引导学生得出有价值的变式,使学生跳出题海,找出题源,举一反三,以不变应瞬变,为备考做充分准备；第三、在解析几何综合题的复习中,有效利用解题教学进行学生思维训练,使高三习题课更好地贴近数学本质教学,挖掘其重要数学思想方法,在领悟数学思想方法的过程中学会思考,可适当减速,给学生充分的思考时间,只有学生有效地思考,才能发生真正意义上的数学,高度重视解析几何习题探究中归纳、类比、联想等数学方法在数学发生、发展、结论形成过程中的作用,深刻领悟同宗同源解析几何习题的“形散而神不散”,在事物的发展变化中,形成数学思想方法,养成理性思维习惯.授人以鱼,不如授人以渔,结论无用,但过程断然无价,当学生离开数学课堂后,还会留下些有价值的东西…….