集装箱港区疏港道路信号控制交叉口通行能力研究

唐国磊，刘翰卿，王文渊

(大连理工大学 建设工程学部，辽宁 大连 116024)

集装箱港区疏港道路信号控制交叉口通行能力研究

唐国磊，刘翰卿，王文渊

(大连理工大学 建设工程学部，辽宁 大连 116024)

通过建立微观交通仿真模型分析大车混入时饱和流率值和相位损失时间的变化规律，进而推求疏港道路信号控制交叉口通行能力。分析仿真结果发现饱和流率值与大车率呈反比例函数关系，相位损失时间与大车率呈二次函数关系。实例表明：与实际通行能力值相比，采用文中提出的计算方法所得值误差较小，说明该方法合理有效。

交通运输工程；疏港道路；通行能力；饱和流率；相位损失时间

0 引 言

港口集疏运系统是与港口相互衔接、主要为集中与疏散港口吞吐货物服务的交通运输系统，是港口赖以存在与发展的主要外部条件。因此，规划设计集装箱港区疏港道路信号控制交叉口时，合理确定信号控制交叉口的通行能力成为亟待解决的问题之一。然而，集装箱港区疏港道路交叉口交通流中，大型车(集装箱卡车)混入比率高，与以小汽车为主的城市道路交通流有显著差异，现行《城市道路交叉口规划规范》不再适用，有必要研究不同大车混入率(下称大车率，HV)下信号控制交叉口通行能力。

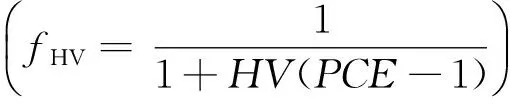
以上对车辆换算系数、大车修正系数和相位损失时间的讨论，主要适用于城市道路中大车率较小的情况，并不完全适用于大车率较高的集装箱港区疏港道路信号控制交叉口通行能力求算。因此，通过建立微观仿真模型，以探求疏港道路交叉口通行能力与不同大车率之间的关系。

1 信号控制交叉口通行能力

GB 50647—2011《城市道路交叉口规划规范》规定，信号控制交叉口进口车道的通行能力(CAPi)应由车道规划饱和流量(Si)与进口车道所属信号相位的绿信比(λi)相乘得到：

CAPi=Si·λi=S0·fHV·λi

(1)

其中，规划饱和流量(Si)应结合进口车道大车率，对基本饱和流量(S0)进行修正确定。规划饱和流量即饱和流率，是假定信号交叉口引道在全绿条件下(即绿信比为1)所能通过的最大流量。当大车率较大时，饱和流率值将大幅降低，因此有必要对大车修正系数(fHV)进行研究。

由于集装箱卡车车身长、机动性差，加减速性能明显不如小汽车，大车混入时，信号相位损失时间将会显著提高，绿信比将显著减小。

依上所述，疏港道路信号控制交叉口通行能力的确定可归结于对饱和流率值(亦即基本饱和流量、大车修正系数)和信号相位绿信比(亦即相位时长、相位损失时间)的确定，其计算图如图1所示。下文将通过建立微观交通仿真模型来分析大车混入时饱和流率值和相位损失时间值的变化规律。

2 微观交通仿真模型建立

微观交通仿真软件VISSIM中车辆的纵向运动(跟车模型)采用Wiedemann建立的生理-心理驾驶行为模型，横向运动(车道变换)采用基于规则的算法[7]。Wiedemann的生理-心理驾驶行为模型是迄今用于计算机交通仿真的最为精确的模型之一，因此VISSIM能较真实反映和重现实际交通状况，在微观交通仿真领域得到了广泛应用[8]。笔者基于VISSIM对疏港道路信号控制交叉口进行微观交通仿真研究，通过分析仿真结果，挖掘大车混入时疏港道路交叉口饱和流率值和相位损失时间的变化规律。

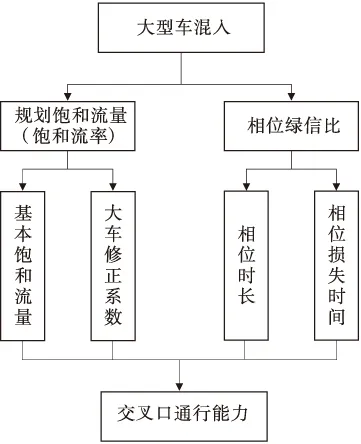
图1 疏港道路信号控制交叉口通行能力求算图Fig.1 The chart of calculating traffic capacity of signalized intersections on collection and distribution road

2.1 仿真模型建立

基于某疏港道路信号控制交叉口建立微观仿真模型。该交叉口进口道路面平坦，无纵坡，车道宽度为3.75 m，左转车道转弯半径约40 m，右转车道转弯半径约25 m(道路几何参数为理想状态)。改变大车混入率时，车道宽度、转弯半径、有无纵坡等道路几何参数并不会对交叉口通行能力的改变产生显著影响，下文不再赘述。

2.2 车辆类型

通过调研集装箱疏港道路信号控制交叉口处交通情况，确定模型中车辆仿真参数：交通流主要由小汽车(标准车)和集装箱卡车(大型车)组成，选取上述两种车型作为微观交通仿真输入车型；小汽车和集装箱卡车的主要性能参数见表1，小汽车期望车速为40～50 km/h，集装箱卡车的期望车速为30～40 km/h。

表1 车辆主要性能参数Table 1 Main vehicle performance parameters

2.3 驾驶行为参数

为使微观交通仿真模型能正确反映现实交通状况，需正确标定模型中的跟驰参数和车道变换参数，它们将深刻影响仿真模型的准确性。选用的跟车模型为Wiedemann 74模型，横向运动选用自由车道选择方式[7]，经校正后车辆的跟驰参数和车道变换参数的标定值见表2[8-11]。

表2 仿真模型参数标定Table 2 Calibrated parameters of the simulation model

2.4 驾驶行为参数标定

采用以下方法对模型参数进行校核与验证：将仿真获得的稳定流车头时距数据与实测数据,进行比较，并对其进行t分布假设检验。

基于t分布假设检验，建立假设H0：假设微观仿真测得的平均车头时距与实测得到的平均车头时距相等。由t检验结果得到，在95%的置信水平下，微观仿真测得的平均车头时距与实测平均车头时距并无显著差异，如表3。因此可以认定采用文中建立的微观仿真模型进行交通仿真所得结果合理有效[12]。

表3 95 %置信度水平下车头时距t检验结果Table 3 “ t ” test of time headway on the confidence level up to 95%

3 通行能力分析

3.1 交叉口饱和流率

根据饱和流率的定义将交叉口某方向进口道信号相位设为全绿(其他方向禁行)，改变交通流构成(即大车率)，运行仿真模型得到不同大车率下该交叉口进口道直行车道的最大交通量，即饱和流率，如表4。

表4 不同大车率下信号控制交叉口饱和流率Table 4 Saturation flow of signalized intersections on different mix rate of heavy vehicle

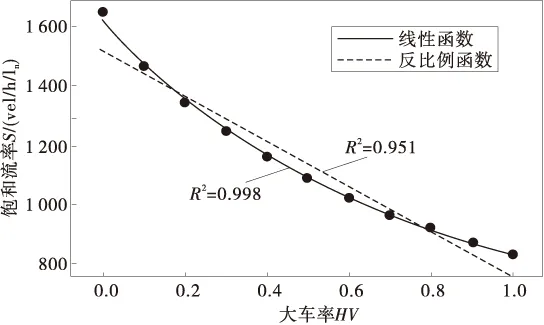
图2 大车率-饱和流率拟合曲线Fig.2 Fitting curves of saturation flow and mix rate of heavy vehicle

如图2，分别用线性函数和反比例函数对表1的数据进行拟合，发现采用反比例函数要比线性函数拟合效果好。因此，求算交叉口饱和流率时，采用反比例函数对大车进行修正更为合理。图2中反比例函数拟合公式为

(2)

进一步仿真发现，对于左转车道、右转车道、直左共用车道以及直右共用车道，饱和流率值与大车混入率也呈反比例函数关系(左转车道饱和流率值S=1 600×1/(1+1.15HV)，右转车道饱和流率值S=1 570×1/(1+1.08HV)，直左、直右共用车道饱和流率值与直行车道饱和流率值相近)。

3.2 相位损失时间

假设某进口车辆可通行相位为P，改变大车混入率和相位P的相位时长(30,40,50,60,70 s)，仿真可得当相位P累计占用时间为1 h时，该交叉口进口道通过的车流量，如图3。

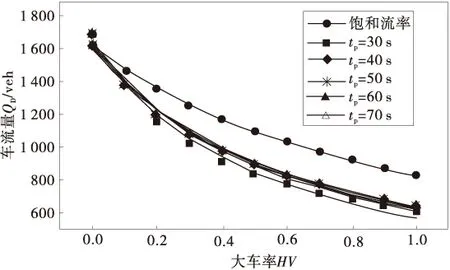
图3 信号控制交叉口大车率-车流量关系Fig.3 Relational graph of traffic volume and mix rate of heavy vehicle on signalized intersections

由图3可以发现，大车率越大、相位时长越小，交叉口通行能力越小。其原因主要是大车加减速性能较差，在绿灯信号控制初期和末期通行流率显著降低，导致相位损失时间加大，有效绿灯时间和绿信比逐渐减小。集装箱卡车混入时，相位损失时间与大车混入率、信号相位时长的关系如图4。

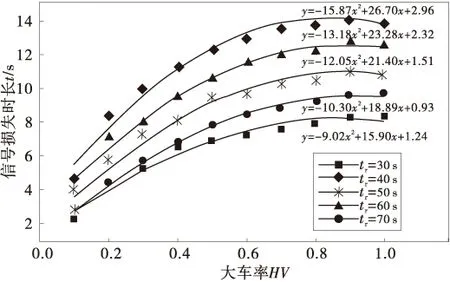
图4 大车率、信号相位时长与相位损失时间关系Fig.4 Relationship between phase lost time and mix rate of heavy vehicle or phase time

由图4可以看出，大车率增大时，相位损失时将从2 s快速增加至10 s以上，相位损失时间与大车率呈二次函数关系。而且，相位损失时间与相位时长有关，相位时间越长，相位损失时间越多，这是由于大小车性能不一致，车辆之间的相互干扰始终存在造成的。

4 应用实例

某集装箱港区疏港道路十字交叉口(如图5)各方向进口道均为双车道，信号相位为两相位(东西向相位时长40 s，南北向相位时长60 s)，东西向车种比例小汽车：集卡为4∶1，南北向车种比例小汽车：集卡为2∶3，道路无纵坡，道路几何参数处于理想状态，试求该交叉口的通行能力。

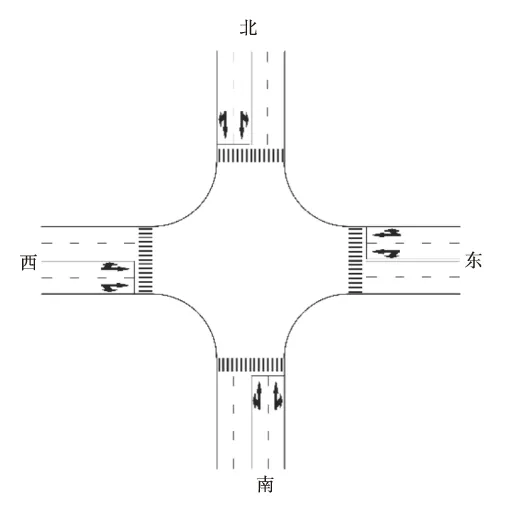
图5 交叉口平面Fig.5 Plane of road intersection

根据式(1)、式(2)及图4，分别计算东西向、南北向的进口道通行能力。以东西向为例，该交叉口东西向进口道通行能力为:

1)饱和流率为

2) 由图4可得，相位损失时间为

t1=-10.30×0.22+18.89×0.2+0.93=4.3s

绿信比为

φ1=(40-4.3)/100=0.36

3) 所以，东西向进口道通行能力为

CAP东，西=1 340×0.36×2=965veh/h

同理，南北向进口道通行能力为

CAP南，北=953veh/h

则该交叉口通行能力为

CAP=965×2+953×2=3 836veh/h

实际调研该进口道通行能力约为3 600veh/h。若采用《城市道路交叉口规划规范》规定的通行能力计算方法，则该交叉口通行能力CAP=1 443veh/h，计算所得值严重偏小，与实际不符。相比之下，由笔者提出的计算方法与实际值相比相对误差较小，说明该方法求算疏港道路交叉口处通行能力合理有效。

5 结 语

当大型车混入时，将对疏港道路交叉口通行能力产生显著影响。通过建立微观仿真模型，分析得出了大车混入下饱和流率值和相位损失时间值的变化规律，并给出了疏港道路信号交叉口通行能力的求算方法。得出以下结论：疏港道路交叉口饱和流率可以通过大车修正系数求得，大车修正系数采用反比例函数比较合适；大车加减速性能对疏港道路交叉口通行能力影响显著，大车混入时，相位损失时间显著增大，相位损失时间与大车率呈二次函数关系。

[1] 同济大学. 城市道路交叉口规划规范：GB50647-2011[S]. 北京: 中国计划出版社, 2011.TongjiUniversity. Code for Planning of Intersections on Urban Roads：GB50647-2011[S].Beijing:ChinaPlanningPress, 2011.

[2] 陈洪仁, 杨龙海, 李丽兰. 基于速度和车头时距的车辆换算系数计算方法研究[J]. 哈尔滨建筑大学学报,2001,34(2):110-114. CHEN Hongren, YANG Longhai, LI Lilan. Analysis of vehicle conversion factor[J].JournalofHarbinUniversityofCivilEhgineering&Architecture,2001,34(2):110-114.

[3] 中交第一公路勘察设计研究院.公路路线设计规范：JTG D20 2006[S]. 北京: 人民交通出版社, 2006. CCCC First Highway Consultants Co., Ltd..DesignSpecificationforHighwayAlignment：JTG D20 2006[S]. Beijing: China Communications Press, 2006.

[4] Transportation Rsearch Board.HighwayCapacityManual2000[S]. Washington, D.C.: National Research Council, 2000.

[5] 陈锦秀, 陈小鸿, 林航飞. 《城市道路平面交叉口规划与设计规程》基本饱和流量与大车校正系数检验研究[J]. 城市交通,2004,2(3):17-20. CHEN Jinxiu, CHEN Xiaohong, LIN Hangfei. Research on verifyingbase saturation flow and heavy vehicle adjust factor in design rugulation for at-grade intersections on urban street[J].UrbanTransportofChina,2004,02(03):17-20.

[6] 王殿海, 杨少辉, 景春光. 累计曲线法计算饱和流率和相位损失时间[J]. 交通运输工程学报,2003,3(3):75-78. WANG Dianhai, YANG Shaohui, JING Chunguang. Cumulative curve method for calculating saturation flow rate and phase lost time[J].JournalofTrafficandTransportationEngineering, 2003, 3(3):75-78.

[7] PTV.VISSIM4.30UserManual[M]. Karlsruhe: Plannning Transport Verkeher AG, 2007.

[8] 罗美清, 隽志才. VISSIM在交叉口交通设计与运行分析中的应用[J]. 武汉理工大学学报(交通科学与工程版),2004,28(2):232-235. LUO Meiqing, JUAN Zhicai. Application of VISSIM to transportation design and operation analysis of intersection[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2004,28(2):232-235.

[9] 孙剑, 杨晓光, 刘好德. 微观交通仿真系统参数校正研究[J]. 系统仿真学报,2007,19(1):48-50. SUN Jian, YANG Xiaoguang, LIU Haode. Study on microscopic traffic simulation model systematic parameter calibration[J].JournalofSystemSimulation, 2007, 19(1):48-50.

[10] 杜攀峰, 金双泉, 李嘉. 高速公路路段通行能力仿真研究[J]. 湖南大学学报(自然科学版),2009,36(6):7-12. DU Panfeng, JIN Shuangquan, LI Jia. Simulation analysis of expressway capacity[J].JournalofHunanUniversity(NaturalScience),2009,36(6):7-12.

[11] 李志明, 闫小勇. 基于遗传算法的交通仿真模型参数校正方法研究[J]. 交通标准化,2006(4):21-23. LI Zhiming, YAN Xiaoyong. Study on correction method of traffic simulation model based on genetic algorithm[J].CommunicationsStandardization,2006(4):21-23.

[12] 吴志洲, 范宇杰, 张剑桥. 考虑集卡影响的上匝道合流区通行能力模型[J].同济大学学报(自然科学版),2013,41(5):670-675. WU Zhizhou, FAN Yujie, ZHANG Jianqiao. Model of merge capacity under impact of container trucks[J].JournalofTongjiUniversity(NaturalScience),2013,41(5):670-675.

Traffic Capacity of Signalized Intersections on Collection and Distribution Road of Container Port

TANG Guolei，LIU Hanqing，WANG Wenyuan

( Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，Liaoning P.R.China)

The function relationships between saturation flow rate and the phase lost time at the time of entering of large truck was analyzed through the establishment of microscopic traffic simulation model to further obtain the traffic capacity at signal-controlled intersection of port road. The results of simulation reveal that the saturation flow value and heavy truck rate is in the functional relationship of inverse proportion while the phase lost time value and rate of heavy trucks is in quadratic function relationship. Practical examples show that the calculated value resulted by the method proposed is very close to the actual traffic capacity value without little deviation, which justifies the rationality and effectiveness of this given method.

traffic and transportation engineering;collection and distribution road； traffic capacity；saturation flow；phase lost time

10.3969/j.issn.1674-0696.2016.04.26

2015-04-20；

2015-08-09

国家自然科学基金项目(51309049，51109030)

唐国磊(1980—)，男，山东烟台人，副教授，博士，主要从事港口规划、港口系统仿真优化等方面的研究。E-mail:tangguolei@dlut.edu.cn。

刘翰卿(1990—)，男，江苏盐城人，硕士研究生，主要从事港口规划、港口系统仿真优化等方面的研究。E-mail:liuhanqingdlut@163.com。

U651

A

1674-0696(2016)04-133-04