两端一般支承裂纹管道的动力学特性

包日东， 梁　峰

(沈阳化工大学，沈阳　110142)



两端一般支承裂纹管道的动力学特性

包日东， 梁峰

(沈阳化工大学，沈阳110142)

摘要：研究了两端一般支承输流管道在含有圆周非贯穿裂纹时的动力学特性。在梁模型横向弯曲振动模态函数中加入3次多项式构造出含裂纹梁的模态函数，根据特征方程具体分析了弹性支承刚度、平均流速、裂纹圆周角、裂纹位置等对系统的固有频率特性和失稳临界流速的影响。数值计算结果表明，由于裂纹的存在，管道的固有频率和静态失稳和动态失稳临界流速将发生复杂的变化。

关键词：输流管道；裂纹；动力学特性；固有频率；临界流速

输流管道在安装和操作过程中，由于多种原因可能导致管道发生损伤，如腐蚀、疲劳、过载、冲击等，裂纹是损伤中典型的一种形式。管道裂纹的出现将改变结构的刚度、阻尼和质量，从而导致结构的动力学特性发生变化。

含裂纹梁的动力学问题的研究已有大量报道[1-3]，但对于含裂纹输流管道流固耦合系统的研究则刚在起步阶段。Yoon等[4-5]首次研究了含裂纹的悬臂输流管道和简支输流管道在移动载荷作用下的动态特性。蔡逢春等[6-8]在Yoon的研究基础上，探讨了含裂纹悬臂输流管道的稳定性，讨论了裂纹位置和深度对频率和颤振临界流速的影响，研究了两端铰支输流管道在振荡流作用下的非线性动力学特性。

本文研究两端受线性弹簧支承和扭转弹簧约束一般支承的输流管道在含有圆周非贯穿裂纹时的固有频率特性和静态失稳及动力失稳临界流速。在梁模型横向弯曲振动模态函数加入3次多项式构造含裂纹梁的模态函数，根据特征方程具体分析了弹性支承刚度、平均流速、裂纹圆周角、裂纹位置等对系统的固有频率特性和失稳临界流速的影响。

1系统运动方程

如图1所示的输流管道，两端受线性弹簧支承和扭转弹簧约束的一般支承情况，其运动方程为[9-10]：

图1　一般支承裂纹管道模型Fig.1 Model of a commonly supported pipe with crack

(1)

式中：U为流体流速;mf为单位长度流体质量;m为单位长度管道的总质量;Af为管道过流截面积;P为流体压强;ν为泊松比;η为Kelvin-Voigt黏弹性系数;E为管材弹性模量;I为管道截面模量;EI为管道抗弯刚度;T为轴向力;x为管道截面位置坐标;y为管道横向振动时的变形。

引入如下的量纲一变量：

(2)

将式(1)化为量纲一形式：

2模态函数

考虑含有一条裂纹的梁(见图1)，从裂纹处将梁分成2段，在裂纹处因转角不连续，用无质量的扭转弹簧模拟裂纹，裂纹梁的模态函数可分段表示为：

A1+A2x+A3x2+A4x3,(0≤x≤xc)

(4)

A5+A6x+A7x2+A8x3,(xc≤x≤L)

(5)

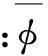
(6)

(7)

一般支承裂纹管道在端部应满足线性弹性支承和扭转弹簧约束的边界条件，在裂纹处应满足位移、弯矩、剪力和转角四个协调条件：

(8)

式(8)中：C为管道外壁圆周裂纹带来的局部柔度系数。将式(4)～(7)代入边界条件为式(8)，可得：

(9)

考虑两端对称支承的情形，即：

KT1=KT1=KT,K1=K2=K

(10)

令：

(11)

将式(11)代入式(9)，可得

(12)

式(12)构成关于Ai(i=1,2,…,8)的线性方程组，求解该方程组，可以唯一确定系数Ai，由此得到裂纹管道的两段模态函数。

3局部柔度系数

假设裂纹尖端应力在弹性范围内，将含单边直裂纹圆管的裂纹区域分割成一序列无限小的矩形条带区域(见图2)，各个微小裂纹条带的应力强度因子近似使用无限长板条的单变裂纹应力强度因子，然后求得直裂纹的柔度系数。依据线性断裂力学理论可计算出在纯弯矩作用下由外壁部分圆周裂纹带来的局部柔度系数为：

(13)

图2　裂纹管道截面Fig.2 Section of the cracked pipe

可进一步将局部柔度系数化为无量纲形式：

(14)

4运动方程的离散

令以上各种边界条件下的模态函数中L=1，即得到无量纲的模态函数。

(15)

将式(15)代入式(3)可得

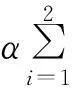
(16)

式(16)两边同乘以φj(ξ),(j=1,2)，然后在区间[0，1]上进行积分，可得

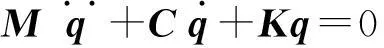
(17)

式中：M，C，K的表达式分别为

C=αB1+2β0.5uB2,K=B1+(u2+p-Γ)B3

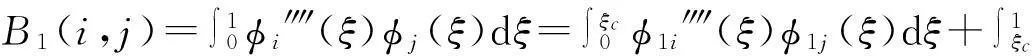
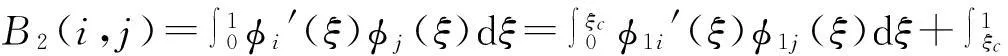
q=(q1,q2)T,(i,j=1,2)

进一步将系统运动方程(17)化为：

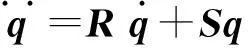
(18)

式中：

R=-M-1C,S=-M-1K

(19)

式中：

这里，rij，sij(i,j=1,2)为矩阵R，S的元素。

5动力学特性分析

式(19)中A的特征方程为

ω4+P1ω3+P2ω2+P3ω+P4=0

(20)

式中：

仿真参数取：α=0.002，β=0.2，Γ=5，p=5，γ=10，u=3，kt=300，k=300，d=Di/De=0.925 9，a/h=0.5，θ=π/6，ξc=0.5。当讨论某参数对固有频率和临界流速的影响时，该参数取变化的值(图中的横坐标)。数值仿真结果见图3～图9，分析和讨论如下。

图3　管道固有频率随弹性支承系数k的变化Fig.3 Variation of natural frequencies with elastic coefficient k

图4　管道固有频率随平均流速u的变化Fig.4 Variation of natural frequencies with mean flow velocity

(1) 图3所示为裂纹管道与无裂纹管道固有频率随端部弹性支承系数k的变化情况比较。从图3可知，两种管道的固有频率随弹性支承系数的变化趋势一致，都随着弹性支承系数的增大而增大，但是，裂纹管道的一阶固有频率比无裂纹管道的一阶固有频率有所降低，而二阶固有频率则有所升高。

(2) 图4是管道固有频率随平均流速u的变化规律。从图4可知，管道的固有频率随内流流速的增大而下降，当一阶固有频率下降到零时，管道便发生屈曲，也即是静态失稳现象。从图中得出，裂纹管道的静态失稳临界流速大于无裂纹管道的静态失稳临界流速，这主要是因为管道系统的总刚度由于裂纹的出现而减小的缘故。另外,从图4也可知，两种管道的一阶和二阶静力失稳会发生耦合，而对于较小的弹性系数，则不会发生一阶和二阶的耦合现象。

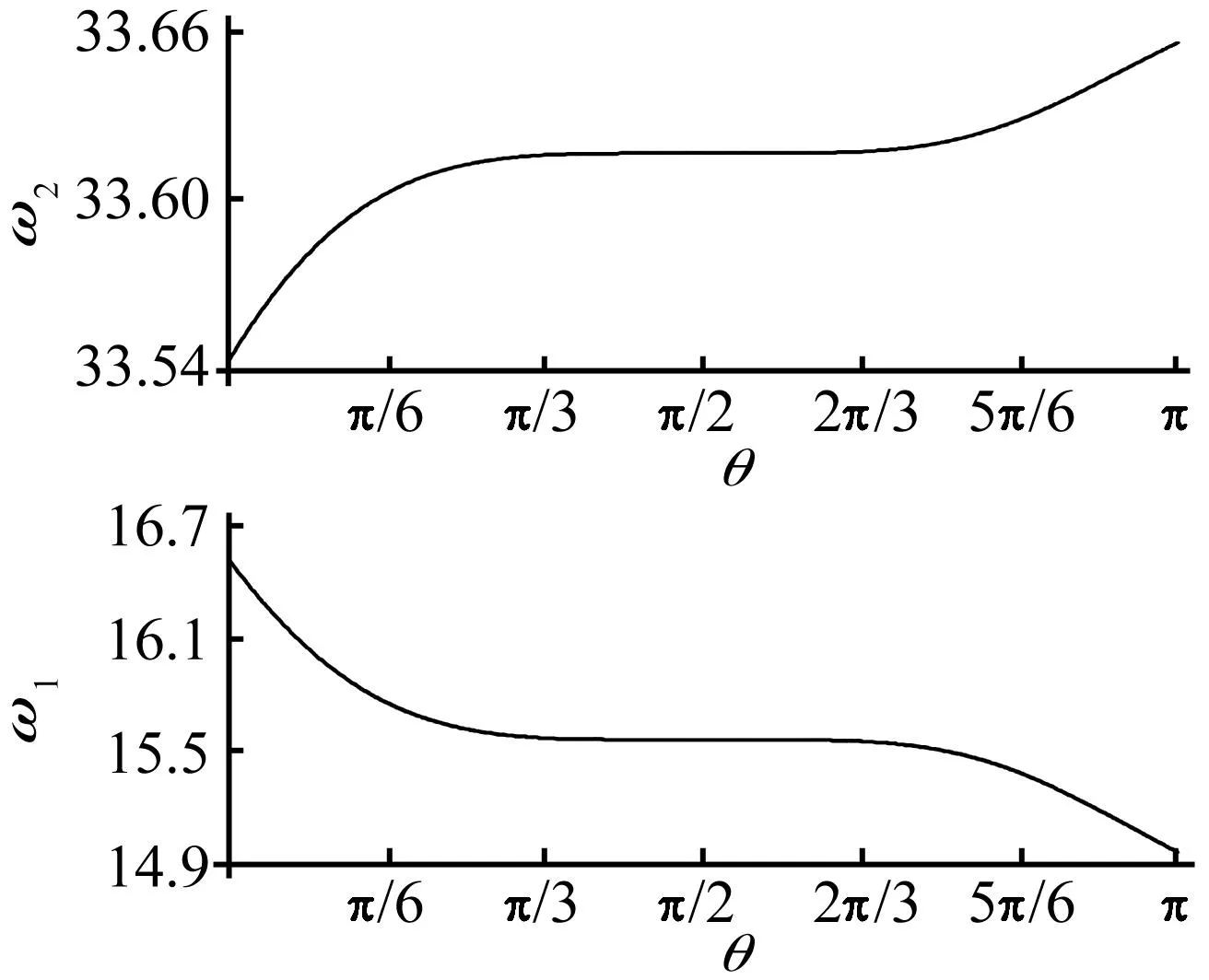
图5　管道固有频率随裂纹圆周角θ的变化Fig.5 Variation of natural frequencies with circumferential angle of crack θ

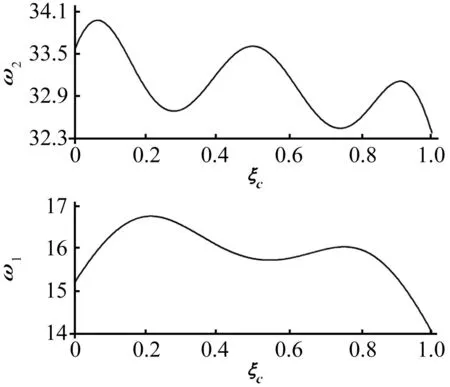
图6　管道固有频率随裂纹相对位置ξc的变化Fig.6 Variation of natural frequencies with relative location of crack ξc

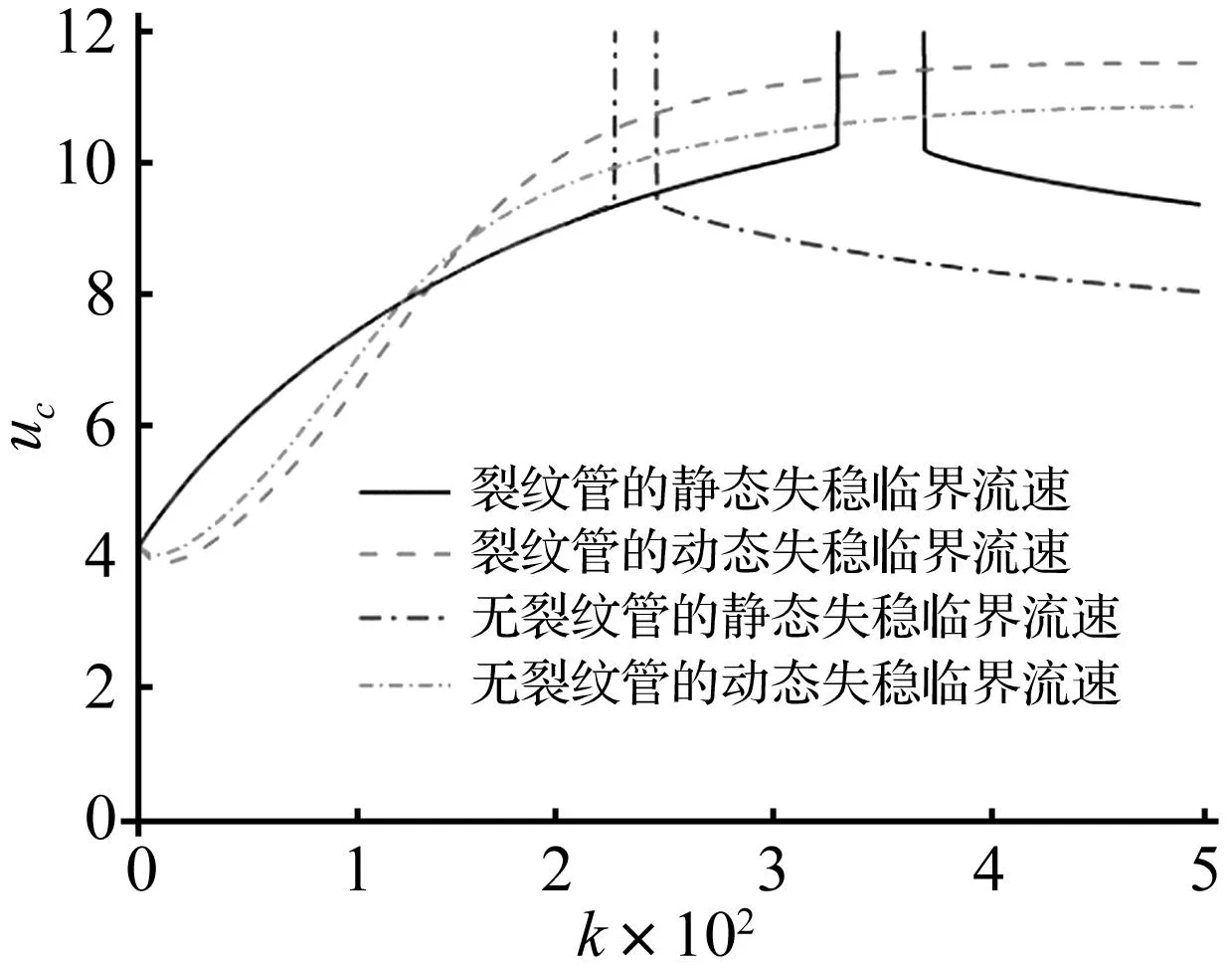
图7　失稳临界流速随弹性支承系数k的变化Fig.7 Variation of critical instabilityflowrate with elastic coefficient k

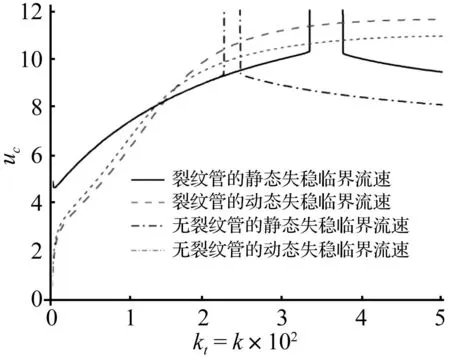
图8　失稳临界流速随弹性系数k和kt的变化Fig.8 Variation of critical instability flowrate with elastic coefficient k and kt

图9　失稳临界流速随裂纹相对位置ξc的变化Fig.9 Variation of critical instabilityflowrate with relative location of crack ξc

(3) 图5为管道固有频率随裂纹圆周角θ的变化情况。从图5可知，管外非贯通裂纹的圆周角增大时，管道的一阶固有频率下降，而二阶固有频率上升，在[0～π/6]和[5π/6～π]区间内，一阶固有频率下降较快，二阶固有频率上升较快，在中间区间内的变化相对较平缓。

(4) 图6为管道固有频率随裂纹相对位置ξc的变化情况。从图6可知，固有频率随裂纹位置的变化呈现出波形变化的规律。一阶固有频率出现了二波，而二阶固有频率出现了三波。

(5) 图7和图8为管道失稳临界流速随两端弹性刚度系数的变化规律。从图7和图8可知，在一定区域的弹性约束刚度kt下，管道的动态颤振失稳临界流速小于静态发散失稳临界流速，也即管道首先发生动态颤振失稳，在较大的弹性支承刚度k下，管道的失稳形态则相反，发散失稳临界流速小于颤振失稳临界流速，即管道先发生发散失稳。另外，从图7和图8还可知，管道的静态发散失稳临界流速有一突变区间，在此突变区间之前，管道的静态发散失稳临界流速随着k的增大而增大，在此突变区间，管道的静态发散失稳临界流速则随着k的增大而减小，最后趋于一个定值，当kt和k足够大时，此定值为两端固定管道的静态发散失稳临界流速值。裂纹管道的这一静态发散失稳临界流速突变区间比无裂纹管道的突变区间大且向后(即向较大的弹性支承系数)变化。在出现此突变区间之前，两种管道的静态失稳临界流速基本相同，而在此之后，则出现裂纹管道的静态失稳临界流速大于无裂纹管道的静态失稳临界流速值。

(6) 图9为失稳临界流速随裂纹相对位置ξc的变化规律。从图9可知，裂纹在管道中点时静态失稳临界流速达到最大值，裂纹向管道两端移动时静态失稳临界流速值下降。动态失稳临界流速有相似的规律，但比静态失稳临界流速的变化较急剧和复杂，特别是裂纹移动到管道的后半部分时变化有较大的波动现象。

6结论

输流管道两端理想支承(简支或固支)是支承条件的理想化模型，工程实际中的支承情况往往介于这两种理想支承之间的中间状态，所以无论采用哪种理想支承来分析输流管道的动力特性，其结果必然与实际情形有较大出入。本文研究的端部受线弹簧支承和扭转弹簧约束的一般支承管道系统，在含圆周非贯穿裂纹时的动力学特性，两端的弹性系数可根据管道实际工况情形来选取，分析比较灵活，能较好地仿真工程中管道实际支承情况。

参 考 文 献

[ 1 ] Khiem N T, Lien T V. A simplified method for natural frequency analysis of a multiple cracked beam[J].Journal of Sound and Vibration, 2001, 245(4):737-751.

[ 2 ] Binici B. Vibration of beams with mulitiple open cracks subjected to axial force[J].Journal of Sound and Vibration, 2005, 287(1/2):277-295.

[ 3 ] Caddemi S, Callio I. Exact closed-form solution for the vibration modes of the euler-bernoulli beam with multiple open cracks[J].Journal of Sound and Vibration, 2009, 327(3/4/5):473-489.

[ 4 ] Yoon H I,Son I S. Influence of tip mass on dynamic behavior of cracked cantilever pipe conveying fluid with moving mass[J]. Journal of Mechanical Science and Technology (KSME Int.J.), 2005,19(9):1731-1741.

[ 5 ] Yoon H I,Son I S. Dynamic behavior of cracked simply supported pipe conveying fluid with moving mass[J]. Journal of Sound and Vibration, 2006, 292(3):941-953.

[ 6 ] 蔡逢春, 臧峰刚, 叶献辉. 含裂纹悬臂输流管道稳定性分析[J]. 核动力工程, 2011, 32(3):116-121.

CAI Feng-chun, ZANG Feng-gang, YE Xian-hui. Stability of cracked cantilevered pipes conveying fluid[J]. Nuclear Power Engineering, 2011, 32(3):116-121.

[ 7 ] 叶献辉, 蔡逢春, 臧峰刚, 等. 含裂纹悬臂输流管道颤振分析[J]. 振动与冲击, 2011, 30(9):169-173.

YE Xian-hui,CAI Feng-chun, ZANG Feng-gang, et al. Flutter of cracked cantilever pipes conveying fluid[J]. Journal of Vibration and Shock, 2011, 30(9):169-173.

[ 8 ] 蔡逢春, 臧峰刚, 梁艳仙. 含裂纹两端铰支输流管道在振荡流作用下的非线性动力学特性研究[J]. 振动与冲击, 2012, 31(4):162-167.

CAI Feng-chun, ZANG Feng-gang, LIANG Yan-xian. Nonlinear dynamic behaviors of a cracked hinged-hinged pipe conveying pulsating fluid[J]. Journal of Vibration and Shock, 2012, 31(4):162-167.

[ 9 ] 包日东,闻邦椿. 分析弹性支承输流管道的失稳临界流速[J]. 力学与实践, 2007,29(4): 24-28.

BAO Ri-dong, WEN Bang-chun. Analysis of critical instability flowrate of pipeline conveying fluid with elastic supports[J].Mechanics in Engineering, 2007,29(4): 24-28.

[10] 包日东, 金志浩, 闻邦椿. 端部约束悬臂输流管道的动力学特性[J]. 工程力学, 2009,26(1): 209-215.

BAO Ri-dong, JIN Zhi-hao, WEN Bang-chun. Dynamical behaviors of restrained cantilever pipe conveying fluid[J]. Engineering Mechanics, 2009,26(1): 209-215.

Dynamic characteristics of a cracked pipe conveying fluid with both elestically supported ends

BAORi-dong,LIANGFeng(Shenyang University of Chemical Technology, Shenyang 110142, China)

Abstract:The dynamic characteristics of a cracked pipe conveying fluid with both ends supported elastically were studied. The bending vibration modal functions of the cracked pipe were derived using the general beam modal functions adding a cubic polynomial. The influences of elastic stiffness coefficients, mean flow velocity, circumference angle of crack and crack position on the natural frequencies and fluid critical flow velocity of the pipe system were simulated and analyzed based on the eigenequation of the piping system. The numerical results showed that the natural frequencies and the fluid critical flow velocity vary complicatedly due to crack existing.

Key words:pip conveying fluid; cracked pipe; dynamic characteristics; natural frequencies; critical flow velocity

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.034

收稿日期：2014-10-28修改稿收到日期：2015-02-06

基金项目：国家自然科学基金资助项目(51275315)

第一作者 包日东 男，博士，教授，1967年生