基于在线测量的滚动直线导轨副精度保持性测试方法及试验研究

姬中晴， 欧　屹， 冯虎田， 张　云

(南京理工大学 机械工程学院，南京　210094)



基于在线测量的滚动直线导轨副精度保持性测试方法及试验研究

姬中晴， 欧屹， 冯虎田， 张云

(南京理工大学 机械工程学院，南京210094)

摘要：针对滚动直线导轨副精度保持性检测要求，提出了一种基于激光位移传感器测距的滚动直线导轨副运动精度在线检测方法。根据相对运动定理，该方法将4个激光位移传感器在线测量的滑块相对导轨基准的距离变化量转化成导轨平行度和滑块偏转角的变化量。通过滚动直线导轨副精度保持性测试方法，在线测量滚动直线导轨副在实际运行过程中的精度损失量，并与滚动直线导轨副的离线数据对比，有效验证了测试原理的可行性。随后，从多方面进行了误差分析。

关键词：滚动直线导轨副；精度保持性；试验研究；在线测量

滚动直线导轨副具有定位精度高，摩擦阻力小，装配简单、寿命长等优点而广泛应用于专用机床、数控机床和加工中心等设备，已成为精密数控设备的关键功能部件[1]。滚动直线导轨副精度可靠性的衡量标准为精度保持性。精度保持性是指滚动直线导轨副在规定条件下和规定时间内精度保持在某一范围而不丧失的能力[2]，是评价机床中使用滚动直线导轨副可靠性的重要指标，也是国内产品与国外产品重要差距所在。所以，从提高国内滚动直线导轨副的产品性能出发，很有必要对滚动直线导轨副的精度保持性测试理论和方法进行研究。

滚动直线导轨副精度的检测方法主要有手动测量和自动化测量两种。传统的测量方法以手动离线测量为主，但离线测量具有一定的局限性，首先它是静态测量，不能描述导轨工作时的精度损失特性。其次，不能确保工作和测量时导轨能在同一基准下进行精度损失的检测。目前我国导轨精度保持性自动化检测装备的研究比较滞后，一般自动化检测只是一种检测装置，不能在同一基准下模拟实际工况进行精度保持性试验和检测。

本文提出了一种基于使用激光位移传感器进行在线测量的精度保持性试验方法，用于描述和检测滚动直线导轨副运动精度的变化。通过一组激光位移传感器相对基准面距离的实时测量数据，得出滑块中心在运动过程中的平行度和偏转角变化量，解决了滚动直线导轨副在线测量的难题，为开展精度保持性试验提供了测试依据。同时开展了大量对比验证试验，证明了本方法的可行性与准确度。

1滚动直线导轨副精度保持性试验装置

精度保持性试验及在线检测方法基于南京理工大学自主研发的滚动直线导轨副精度保持性试验台，该试验台能够在模拟实际工况的条件下进行精度保持性试验[3]。试验装置见图1。

图1　滚动直线导轨副精度保持性试验台Fig.1 The test bench of linear rolling guide movement precisiontest-bed

试验台激光位移传感器安装方式见图2。传感器1、传感器2对称分布于滑块侧面两端，测量滑块侧面相对导轨同侧侧面基准的平行度以及滑块相对导轨的偏摆角变化量；传感器3、传感器4对称分布于滑块顶面中心处两侧，测量滑块顶面相对导轨底面基准的平行度以及滑块相对导轨的俯仰角变化量。

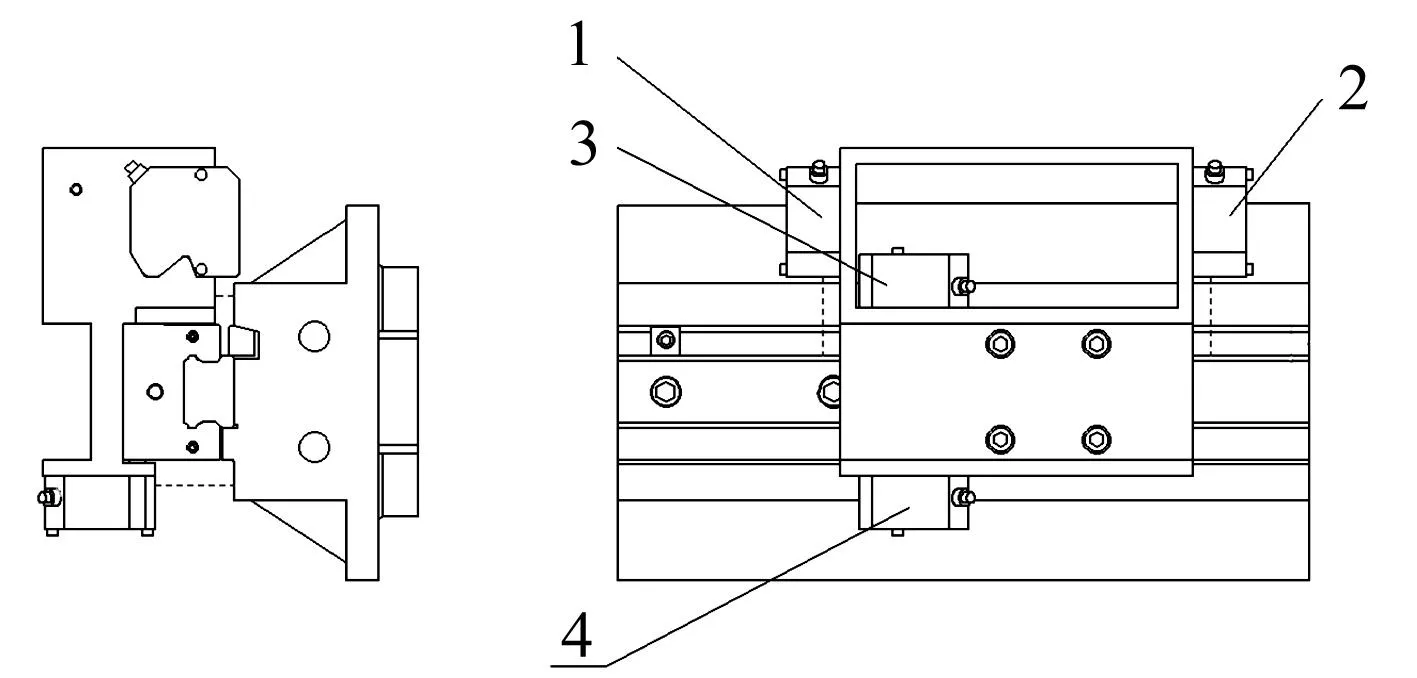
图2　激光位移传感器安装图Fig.2 Installation diagram of laser displacement sensor

2滚动直线导轨副精度检测方法

2.1滚动直线导轨副精度的离线检测方法

滑块移动对导轨的平行度是滚动直线导轨运动精度的具体指标。根据滚动直线导轨副验收技术条件，精度的离线检测主要包括：① 滑块移动对导轨底面基准A的平行度；② 滑块移动对导轨侧面基准B的平行度[4]。具体检测方法见图3。

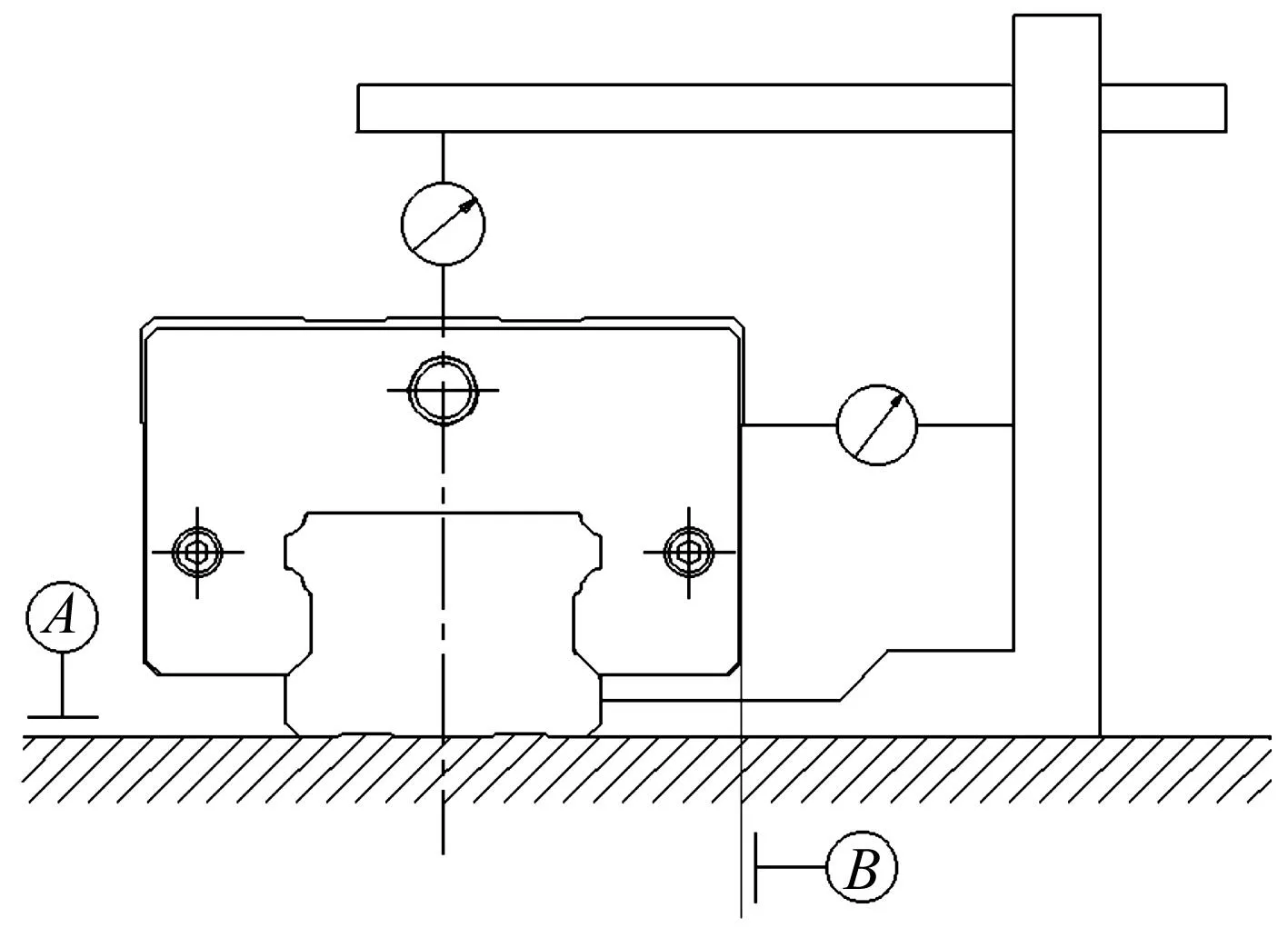
图3　导轨离线测量原理图Fig.3 Schematic diagram of the guide off-line measurement

这种传统的导轨精度离线检测方法较之在线检测有以下不足：① 离线检测为静态手动测量，不能实时监测导轨正常工作时的运动精度损失情况；② 每次离线测量必须放在专门的高平面度检测台上，拆装困难，检测效率低。③ 导轨工作时的安装基准和检测台基准不能确保基准的同一性。

2.2滚动直线导轨副精度的在线检测方法

滚动直线导轨副在使用一定时间后，导轨、滑块及滚动体之间会产生接触变形和磨损，导致滚动体接触角改变及滑块位移。滚动直线导轨副精度保持性试验台可在线检测滑块移动对基准面的平行度以及滑块相对导轨的偏转角度变化量。

设定滑块在导轨最左端时的几何中心为原点O，分别以垂直滑块侧面、顶面、端面为X、Y、Z轴建立基准坐标系O-XYZ。滑块运动了任意距离L后，坐标系为O′-X′Y′Z′(见图4)。

图4　滚动直线导轨副坐标系Fig.4 The linear rolling guide coordinate system

滑块在运动过程中基准坐标系在X轴和Y轴方向有偏移，并绕Y轴和Z轴产生偏转。根据精度的检测方法，在X轴和Y轴的偏移量ΔX、ΔY即为侧面平行度和顶面平行度的变化量，在导轨全长上测得的ΔX、ΔY中，最大的变化量maxΔX和maxΔY即分别为滑块侧面对导轨同侧侧面基准的平行度、滑块顶面对导轨底面基准的平行度。滑块端面绕Y轴的偏摆角Δδ为滑块相对导轨的偏摆角变化量；滑块顶面绕Z轴的翻转角ΔΦ为滑块相对导轨的俯仰角变化量。

2.2.1偏转角和俯仰角的计算

测量偏摆角的变化量时，假设滑块相对导轨先发生俯仰变化，再发生偏摆。根据相对运动定理，将滑块视为定物，导轨基准侧面相对滑块进行俯仰和偏摆(见图5)。滑块俯仰后，传感器1、传感器2示数以相同大小增加或减小X；滑块偏摆后，传感器1、传感器2示数发生变化。偏摆角变化量的正切函数等于其示数差与其安装距离之比，如式(1)所示：

(1)

式中：R1、R2为位移传感器1、传感器2到对应基准面的初始距离；R1′、R2′为位移传感器1、传感器2到对应基准面的实际距离；L(1-2)为位移传感器1、传感器2激光间距。

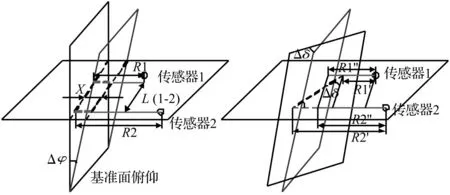
图5　滑块侧面相对导轨先俯仰后偏摆示意图Fig.5 Schematic diagram that the slider side relative to the yaw after pitch of guide

假设滑块相对导轨先发生偏摆，随后发生俯仰(见图6)。则其偏摆角的变化量如式(2)所示：

(2)

图6　滑块侧面相对导轨先偏摆后俯仰示意图Fig.6 Schematic diagram that the slider side relative to the pitch after yaw of guide

由式(1)和式(2)可知，在建立滑块相对导轨的旋转模型时，其偏摆与俯仰的顺序不影响偏摆角的计算。

测量俯仰角的变化量时，假设滑块相对导轨先发生偏摆变化，再发生俯仰。根据相对运动定理，将滑块视为定物，导轨基准底面相对滑块进行偏摆和俯仰(见图7)。滑块偏摆后，由基准面1变为基准面2，传感器3、传感器4示数不变；滑块俯仰后，由基准面2变为基准面3，传感器3、传感器4示数发生变化。俯仰角变化量的正切函数等于其示数差与其安装距离之比，如式(3)所示：

(3)

式中：R3、R4为位移传感器3、传感器4到对应基准面的初始距离；R3′、R4′为位移传感器3、传感器4到对应基准面的实际距离；L(3-4)为位移传感器3、传感器4激光间距。

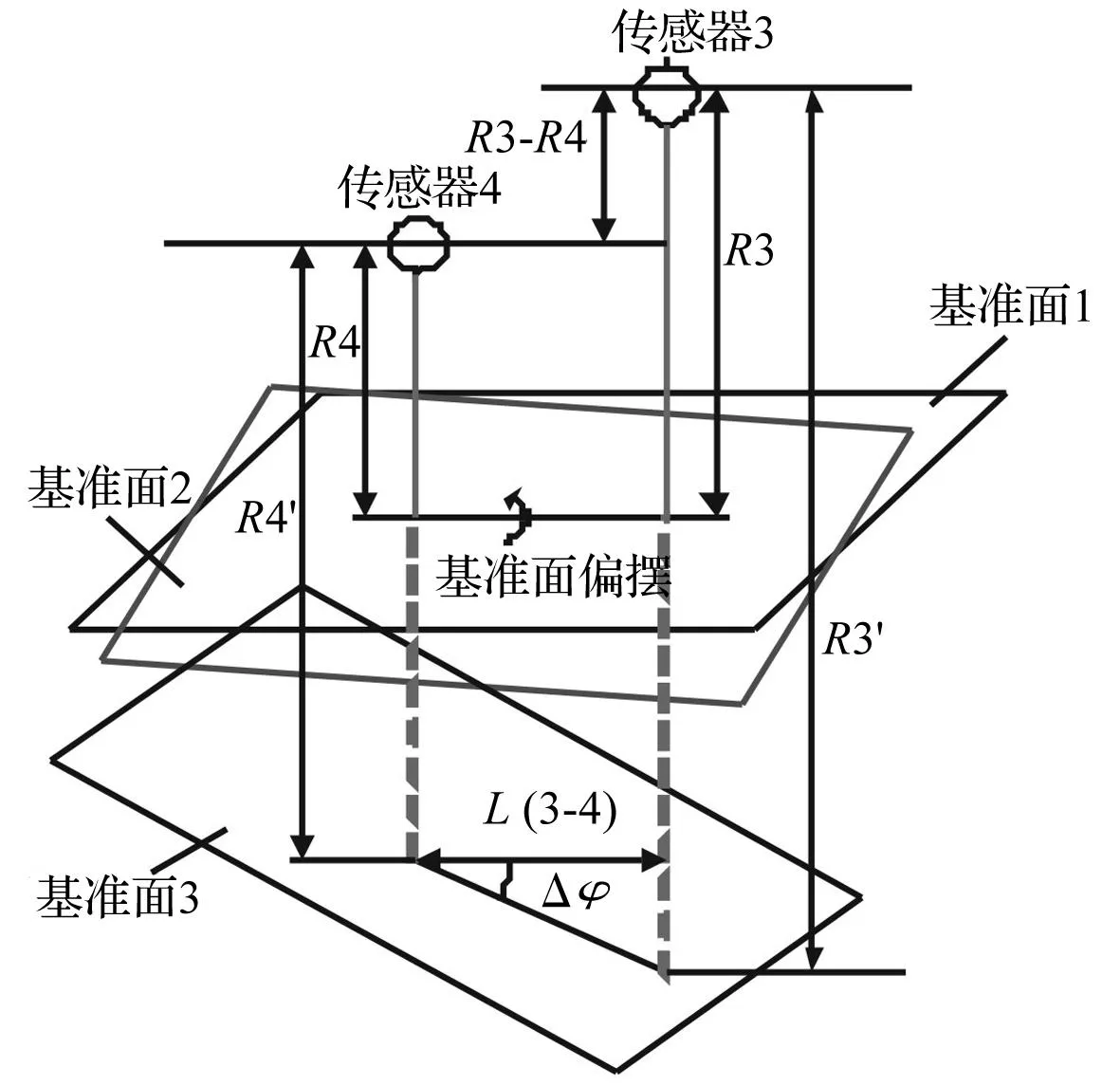
图7　滑块顶面相对导轨先偏摆后俯仰示意图Fig.7 Schematic diagram of the slider top surface relative to the pitch after yaw of guide

假设滑块相对导轨先发生俯仰，随后发生偏摆(见图8)。滑块俯仰后，由基准面1变为基准面2，传感器3、传感器4示数变化；滑块偏摆后，由基准面2变为基准面3，传感器3、传感器4示数不变。其偏摆角的变化量如式(4)所示：

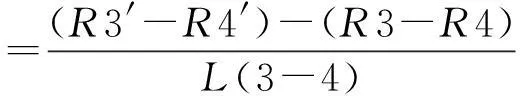
(4)

图8　滑块顶面相对导轨先俯仰后偏摆示意图Fig.8 Schematic diagram of the slider top surface relative to the yaw after pitch of guide

由式(3)和式(4)可知，在建立滑块相对导轨的旋转模型时，其偏摆与俯仰的顺序不影响俯仰角的计算。

2.2.2平行度和精度损失的计算

根据平行度定义将传感器采集数据进行换算，得到滑块顶面中心处及滑块侧面中心处的平行度。

由图9可知，滑块侧面中心处在X轴方向的偏移量ΔX可根据下式计算：

(5)

式中：δ为传感器1、2在Z轴方向的初始角度，其大小如下：

(6)

图9　侧面平行度变化量ΔX计算模型Fig.9 The computational model of side Parallelism’s change ΔX

由图10可知，滑块顶面中心处在Y轴方向的偏移量ΔY可根据下式计算：

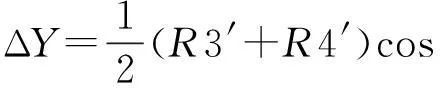
(7)

式中：Φ为传感器3、传感器4在X轴方向的初始角度，其大小如下：

(8)

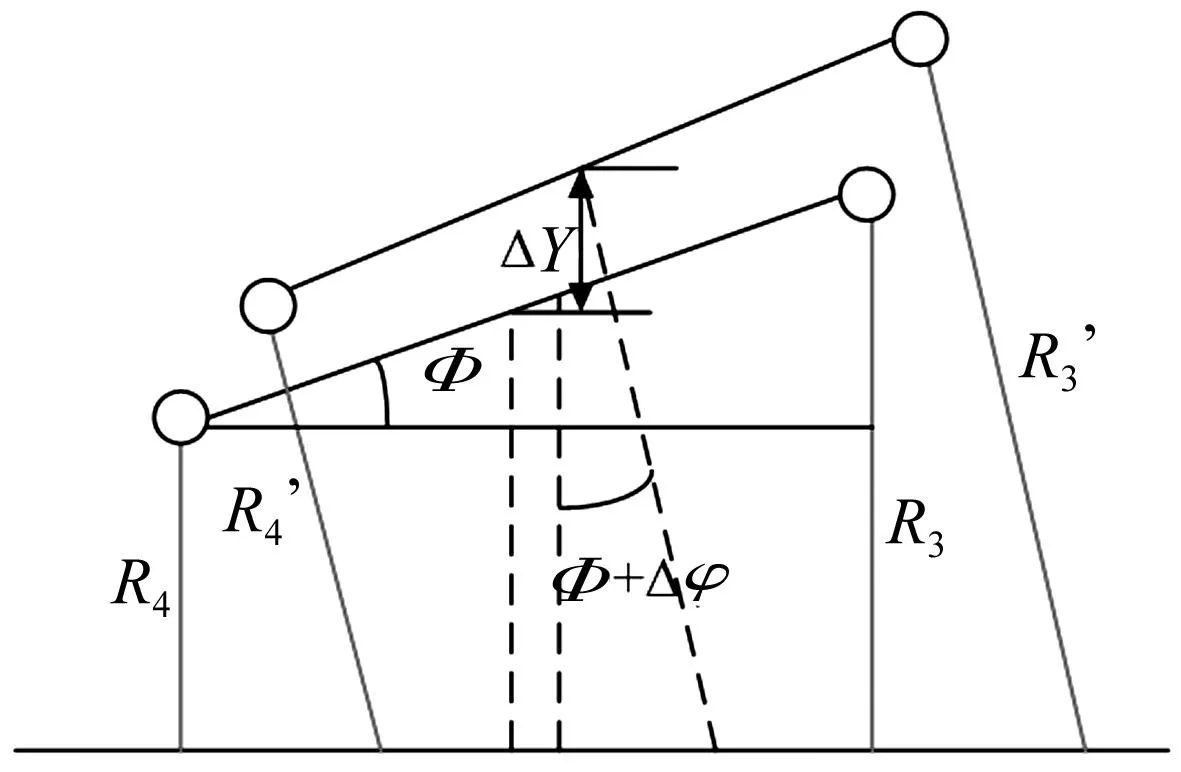
图10　顶面平行度变化量ΔY计算模型Fig.10 The computational model of top Parallelism’s change ΔY

由式(5)、式(6)，可得滑块侧面相对导轨同侧侧面基准的平行度变化量ΔX；由式(7)、式(8)，可得滑块顶面相对导轨底面基准的平行度变化量ΔY。以上模型均适用于基准面为绝对平面时的计算。

在实际测量过程中，由于传感器1、传感器2的激光打在导轨侧面基准上，导轨侧面基准可近似认为是相对平面，因此在测量的ΔX(j)中，取其最大值与最小值之差即为检测的侧面平行度。第一次检测的平行度为maxΔX1，第i次检测的平行度为maxΔXi，从第一次检测到第i次检测的精度损失量为(maxΔXi-maxΔX1),见图11。

图11　导轨侧面测量原理示意图Fig.11 Schematic diagram of the side measuring principle for the guide

传感器3、传感器4的激光打在导轨转接板基准面上，经检测，该转接板的基准面并不是一个绝对平面，其误差相对导轨平行度不容忽略。因此，需对检测的数据进行一定的处理，以得到滑块顶面相对导轨底面基准的平行度。假设第一次检测得到相应点的ΔY为ΔY1(j)，第i次检测得到相应点的ΔY为ΔYi(j)见图12。当检测次数i≥2时，检测时需减去对应点的第一次检测值，得到相对第一次检测的一系列差值{ΔYi(j)-ΔY1(j)}，其中i=0,1,2,3,…;j=0，1,2,3,…。假设其最大值为maxΔYi，最小值为minΔYi，则从第一次检测到第i次检测的精度损失量为(maxΔYi-minΔYi)。

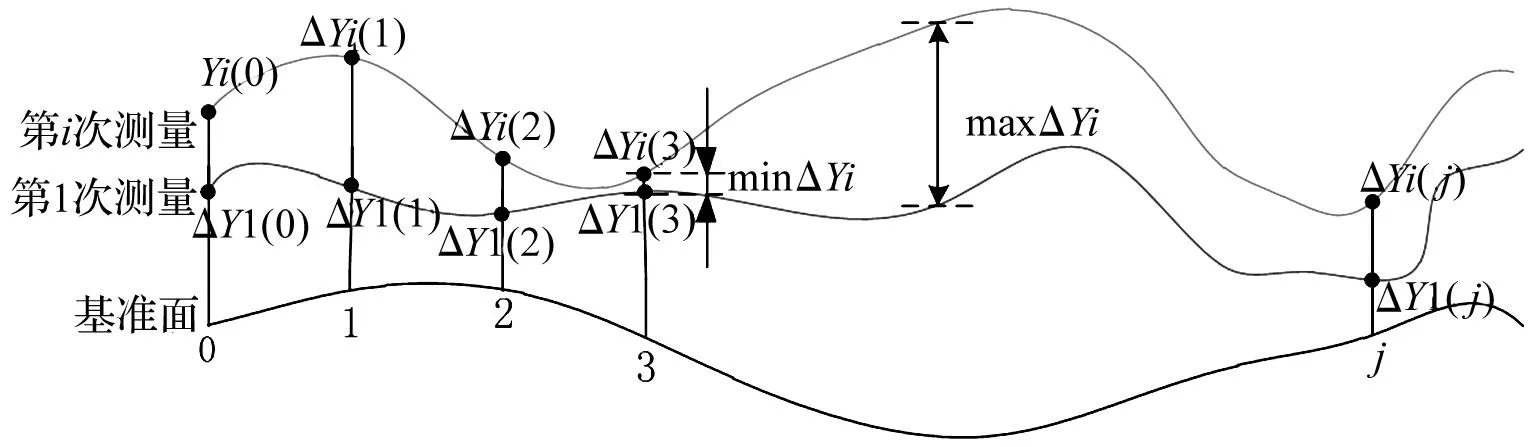
图12　导轨底面测量原理示意图Fig.12 Schematic diagram of the underside measuring principle of guide

3滚动直线导轨副精度保持性试验研究

3.1滚动直线导轨副精度保持性试验分析

滚动直线导轨副精度保持性指标用有效精度保持时间或磨损寿命表示，对于一批产品用磨损寿命可靠度表示[5]。有效精度保持时间是指在规定条件下导轨精度保持在规定的等级范围内而未丧失的时间。磨损寿命可靠度是指在规定条件下一批导轨有效精度保持时间为某一特定值的概率。

精度储备量Ec是指被测滚动直线导轨副样品的标称精度允许值与离线测量实际值的差值[6]，随着导轨在运行时间的增大，滚道与滚珠的磨损会增大，精度损失也会越来越大。

在试验中，当被测样品的运动平行度损失值≥80%Ec时，应停止试验并离线测量。若精度未失效，则计算出新的储备量并继续进行试验。精度保持性测试原理见图13。

图13　精度保持性测试原理图Fig.13 Schematic diagram of movement precision measurement

3.2滚动直线导轨副精度保持性试验

应用以上测量原理，采用国内厂家3级3 000 mm长的导轨在滚动直线导轨副精度保持性试验台上进行试验。根据滚动直线导轨副第四部分验收技术条件[4]，该导轨的顶面与侧面精度离线测量值分别为12 μm和14 μm，标称精度允许值都为20 μm，因此，顶面精度储备量Ec1=8 μm，侧面精度储备量Ec2=6 μm。图14为激光位移传感器安装实物图。

图14　激光位移传感器安装实物图Fig.14 Installation physical diagram of laser displacement sensor

精度保持性试验方案采用滚动功能部件行业标准进行试验和测量[6]，在线测试结果见图15和图16。

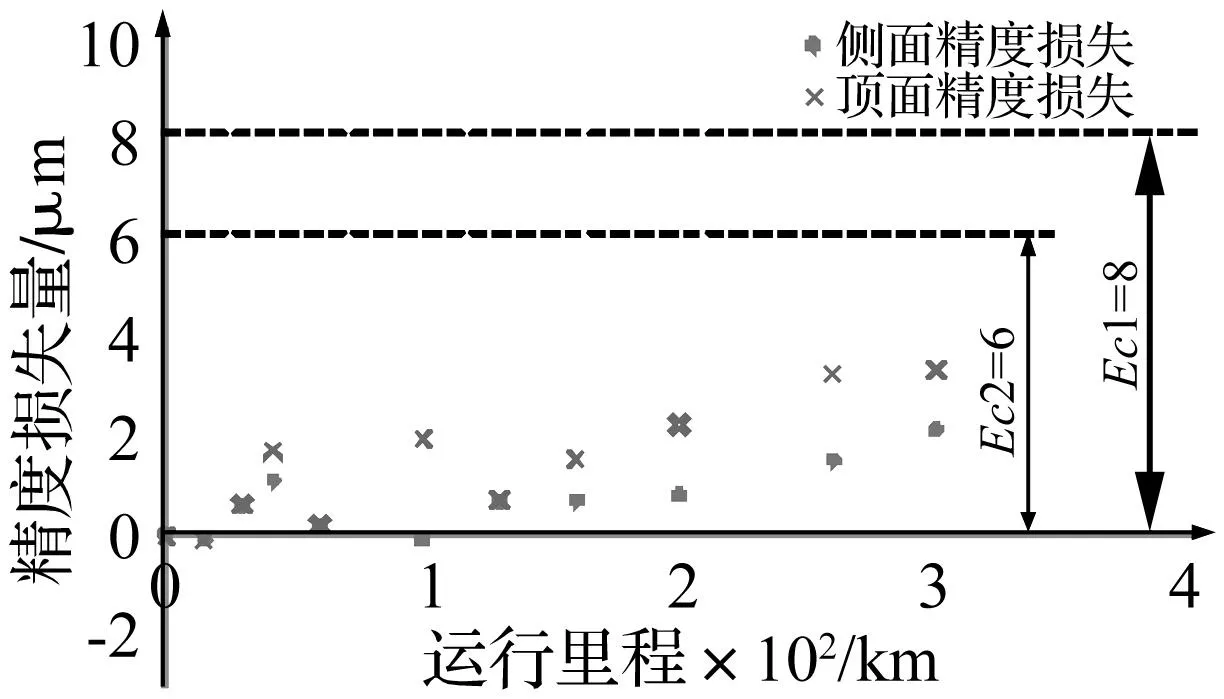
图15　精度保持性精度损失测试结果Fig.15 The Loss of accuracy measurement result of movement precision

图16　精度保持性滑块偏转角测试结果Fig.16 The measurement result of slider deflection angle ofmovement precision

直线导轨的运行是一个磨损过程，其过程可以分为磨合阶段、稳定磨损阶段和急剧磨损阶段。从图16可知，离散数据可以看出随着运行里程的增加，精度损失呈增大趋势。在运行初期，导轨处于磨合过程而出现了一定的波动。屠国俊在试验和论文中也曾表述过这种现象。这说明导轨初期确实存在磨合过程，出现波动现象与实际情况相一致。为了验证测试原理，将导轨300 km时的精度损失量在线测量值与离线测量值进行对比。

由表1可见，在线检测与离线检测所得的精度损失值相差微小，从而验证了在线检测方法的可行性。由于滚珠直线导轨本身寿命较高，试验耗费的时间长，到截稿时试验仍在继续，所以只选取导轨运行300 km时的数据。

表1　精度保持性离线与在线测试结果对比表

4数据误差分析

4.1算法误差

对于滚动直线导轨副，滑块在运动的过程中会

产生俯仰和偏摆。根据布尔沙-沃尔夫模型[7-8]，在滑块在导轨最左侧建立基准坐标系O-XYZ，滑块运动到任意位置时的坐标系为O′-X′Y′Z′，Y轴与Y′轴的夹角即为俯仰角，Z轴与Z′轴的夹角即为偏摆角。在数据处理中，计算侧面平行度时忽略了俯仰角的变化，计算顶面平行度时忽略了偏摆角的变化。由于试验中测得的初始偏转角的角度约为2°×10-3，几乎不影响平行度的测量，因此这个误差可以忽略。

4.2传感器精度误差

滚动直线导轨副精度保持性试验台的精度检测采用的激光位移传感器，测量范围为±10 mm，线性误差为±4 μm。因此，传感器本身测量的时候会带来一定的误差。

4.3安装误差

安装误差对运动精度有比较大的影响，滑块顶面的精度损失是由传感器测量的导轨转接板平面的相对距离得出。虽然该平面与导轨的安装基准底面采用同一道工序加工而成，保证两个平面具有相同的尺寸、表面粗糙度和形位公差，但在安装被测导轨的时候，不能保证两个平面完全平行，因此会给精度检测带来一定的误差。但是，根据文中提到的计算方法，采用对应数据相减得到精度损失量，可以抵消由于安装和基准问题产生的误差。因此，忽略长时间运行床身蠕变可能因素的影响，安装误差对精度保持性试验的影响几乎可以忽略。

4.4其他误差

由滚动直线导轨副精度保持性试验规范可知，润滑油中灰尘及机械杂质的颗粒不应大于10 μm。但被测导轨副处于开放式环境中，润滑油、空气中难免会有杂质颗粒[9]，因此会给精度测量带来必然的不确定的误差。此外，导轨副的预加载荷和测试速度对导轨副的运动精度有一定影响[10-11]。

5结论

本文通过分析滚动直线导轨副精度保持性试验台的结构特性，研究了精度保持性试验台精度在线测试方法，提出了一种由滑块相对基准距离变化换算成滑块移动对基准面的平行度以及滑块相对导轨的偏转角度变化量的测控算法，解决了在线平行度和精度测量问题，为在线测量滚动直线导轨副精度保持性提供了一定指导。

参 考 文 献

[ 1 ] 李薇. 一种滚动直线导轨副精度自动化检测方法[J]. 组合机床与自动化加工技术，2010(3): 34-37.

LI Wei. One automatic measuring method of linear rolling guideway[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2010(3):34-37.

[ 2 ] 屠国俊，陶卫军，冯虎田，等. 基于步进加载的重载滚动直线导轨副可靠性试验方法[J]. 机床与液压，2012,40(5): 4-7.

TU Guo-jun, TAO Wei-jun, FENG Hu-tian, et al. Reliability test method of overloaded linear rolling guide vice based on stepping loading[J].Machine Tool & Hydraulics,2012, 40(5):4-7.

[ 3 ] Tao Wei-jun, Zhong Yang, Feng Hu-tian,et al. Model for wear prediction of roller linear guides[J]. Wear,2013, (305): 260-266.

[ 4 ] JB/T7175.4-2006, 滚动直线导轨副第4部分: 验收技术条件[S]. 北京：机械工业出版社，2006.

[ 5 ] 屠国俊. 滚动功能部件可靠性试验、分析及评估方法研究[D]. 南京:南京理工大学, 2011．

[ 6 ] JB/0802201140000016, 滚动功能部件可靠性第5部分:滚动直线导轨副精度保持性试验规范[S]. 2015.

[ 7 ] 陈宇，白征东，罗腾. 基于改进的布尔沙模型的坐标转换方法[J]. 大地测量与地球动力学，2010, 30(3): 71-78.

CHEN Yu, BAI Zheng-dong, LUO Teng, An improved bursa model for coordinate transformation[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 71-78.

[ 8 ] 张萌，杨志勇，丁克良. 基于改进的布尔沙-沃尔夫模型的任意旋转角坐标转换方法的研究[J]. 北京测绘，2013(1): 16-35.

ZHANG Meng, YANG Zhi-yong, DING Ke-liang. Research on an improved bursa-wolf model for 3D coordinate transformation[J]. Beijing Surveying and Mapping,2013(1): 16-35.

[ 9 ] Tomas J. Prediction of wheel profile wear-comparisons with field measurements[J]. Wear, 2002, 253: 89-99.

[10] Ohta H, Hayashi E. Vibration of linear guideway type recirculating linear ball bearings[J]. Journal of Sound and Vibration, 2000,235: 847-861.

[11] 徐烨，李先锋. 影响滚动直线导轨副运动精度因素的研究[J]. 机械，2000, 27: 60-61.

XU Ye, LI Xian-feng, Study on movement precision influencing factors of linear rolling guide[J]. Machinery, 2000, 27: 60-61.

Measurement method and tests for precision-keeping of a linear rolling guide based on online measuring

JIZhong-qing,OUYi,FENGHu-tian,ZHANGYun(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:Aiming at the checking demands of precision-keeping for a linear rolling guide, a online measuring method for measuring its motion accuracy based on laser displacement sensor was presented. According to the relative motion theorem, using the proposed method, the diatance variations between slider and guide measured with 4 laster displacement sensors were converted into the variations of the guid’s level parallelism and the slider’s deflection angle. Then the online loss of precision of a linear rolling guide in actual running process was measured with the proposed method, and the feasibility of the online measuring principle was validated effectively through comparing the measured results with the linear rolling guide’s off-line data. Finally, error analysis was performed in many ways.

Key words:linear rolling guide; precision maintenance; experimental study; online testing

中图分类号:TH132; P258

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.009

通信作者欧屹 男，博士，讲师，1982年生

收稿日期：2015-02-28修改稿收到日期：2015-04-17

基金项目：国家重大科技专项(2012ZX04002021)

第一作者 姬中晴 女，硕士，1990年生