风机齿轮双裂纹扩展特性及寿命分析

穆塔里夫·阿赫迈德 ，白浩宇 ，孙光耀

(1.新疆大学机械工程学院， 新疆乌鲁木齐 830047；2.新疆大学电气工程学院， 新疆乌鲁木齐 830047)

0 前言

当前对风能利用的形式主要还是风力发电，而增速齿轮箱是风力发电机组中最重要的组成部件之一。齿轮箱中齿轮断裂是最常见的现象，断裂原因主要是长时间的载荷作用导致裂纹萌生及扩展，最后使其齿轮断裂，这会使风机产生严重的故障。因此，对其裂纹特性进行研究和对寿命计算进行分析很有必要。

目前，很多学者对其裂纹扩展及寿命进行了分析。李有堂等探究了考虑闭合效应与不考虑其闭合效应情况下疲劳裂纹扩展寿命的区别。李秀红等通过有限元软件计算与实验结果对比来确定最优裂纹萌生损伤模型，探究载荷及表面粗糙度对裂纹萌生寿命的影响。CAI等探讨了初始裂纹在不同几何参数下的齿根裂纹前缘应力强度因子的变化规律。朱林等人考虑了残余应力影响下的裂纹扩展,预测结果与实验结果基本一致。肖俊峰和李建兰探究了紧急制动对风机行星轮系中太阳轮裂纹疲劳扩展寿命的影响。赵国平等研究了混合润滑对斜齿轮裂纹萌生及扩展寿命的影响。刘杰等人创建了悬臂梁模型，探究裂纹增长对振动响应的影响。有学者分析混合模式对不同三维裂纹疲劳扩展寿命的影响。王延忠等在齿面上探究不同粗糙度对齿轮疲劳寿命的预测影响。许德涛等运用有限元软件，探究初始裂纹在不同参数条件下对裂纹前缘应力强度因子及疲劳扩展寿命的影响。

上述研究主要是针对于齿轮齿根处单条三维裂纹疲劳扩展的问题，通过改变三维裂纹的初始参数讨论对扩展轨迹及疲劳寿命的影响。工程上，一个物体上的两条很靠近的裂纹会被当成一条裂纹处理，但两条相对比较远的裂纹是根据受力情况进行扩展的，在一定条件下可能会融合。风机齿轮齿宽较大，出现双裂纹及多裂纹的概率较大。文中主要讨论风电机齿轮齿根处出现双裂纹的情况，探究含初始双裂纹齿轮在扩展过程中应力强度因子及疲劳寿命的变化规律。

1 应力强度因子与裂纹扩展

1.1 应力强度因子

三维裂纹类型分为：张开型裂纹也被称为Ⅰ型裂纹，滑移型裂纹也被称为Ⅱ型裂纹，撕裂型裂纹也被称为Ⅲ型裂纹。其应力强度因子也对应分为、、。

选取裂纹端点为坐标原点，建立极坐标(,),远小于裂纹长度，轴正方向为裂纹前缘，轴正方向为裂纹面法线方向，轴正方向为裂纹扩展方向。根据断裂力学的解析，裂端的应力场(,,,,,)如图1所示。

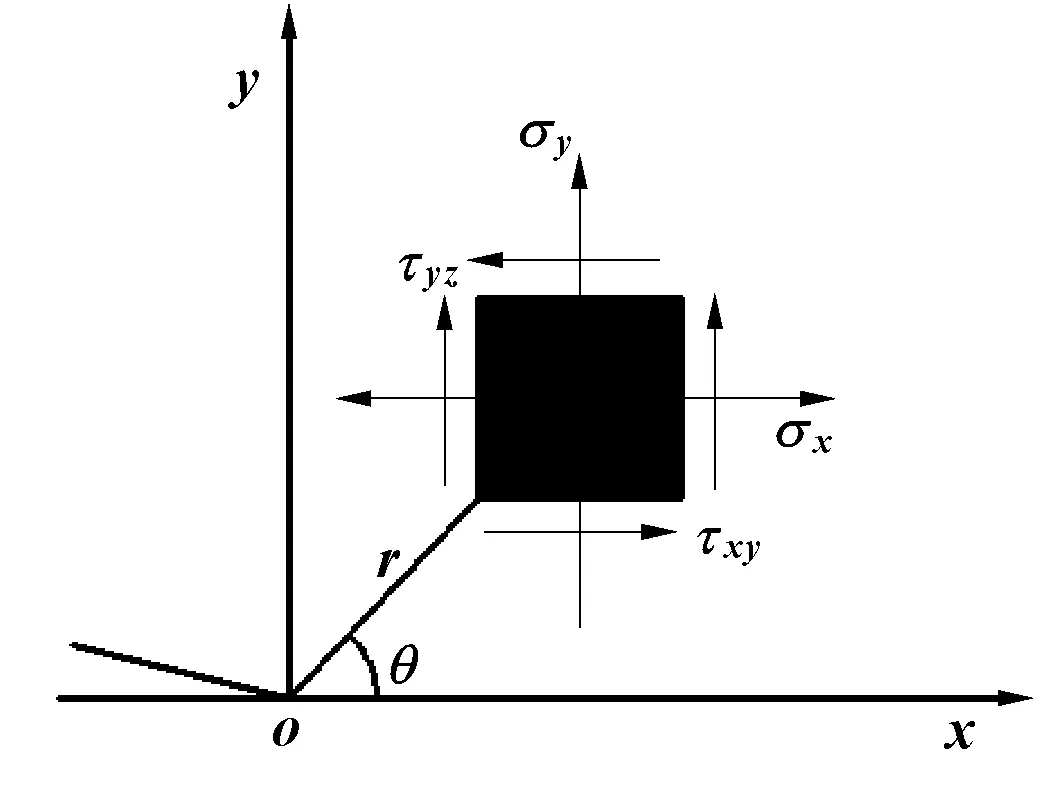
图1 裂纹尖端应力场

裂纹前缘距离裂纹处的渐进应力场可以统一表示为

(1)

式中：()为裂纹形状与外载荷条件下的分布函数；为应力强度因子。3种应力强度因子的公式分别为

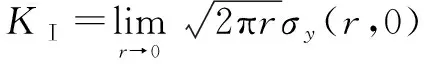
(2)

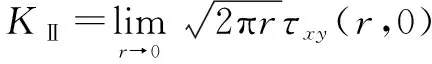
(3)

(4)

1.2 疲劳裂纹扩展

为计算并分析疲劳裂纹扩展的寿命，必须了解疲劳裂纹扩展速率曲线。图2中为裂纹长度，为裂纹扩展循环次数，Δ为裂纹扩展的门槛值，一般由材料决定，Δ为最大应力强度因子减去最小应力强度因子的差值。从图2中可明显地看出该曲线分为3个区域，区域1为低速区，当Δ<Δ时，裂纹被默认为是不扩展的。

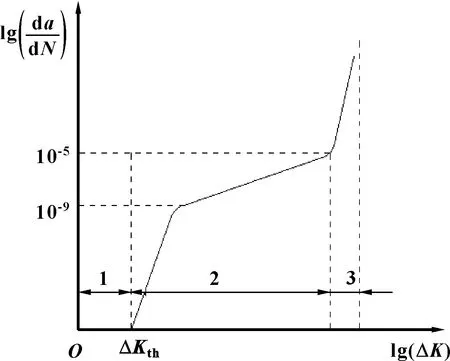
图曲线

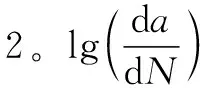
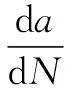
(5)

区域3为高速区，这个区域裂纹扩展速率快，通常不考虑该区域的寿命。

2 建立含初始双裂纹齿轮模型

为分析变速箱齿轮齿根边缘处三维裂纹，首先需要参数化创建三维齿轮模型。齿轮参数：小齿轮的齿数为36，大齿轮的齿数为84，大齿轮与小齿轮模数均为8 mm，压力角均为20°，齿宽均为200 mm，齿顶高系数1，顶系0.25，材料为42CrMn。裂纹导入和裂纹扩展时对网格要求较高，需要导入专业的网格处理软件中进行网格划分。齿轮局部网格如图3所示。

图3 齿轮局部网格划分

划分好网格后，需要导入有限元软件中进行计算，再联合Franc 3D软件插入三维裂纹继续计算。为探究双裂纹应力强度因子的变化规律，需要对小齿轮孔施加一个固定约束，对大齿轮孔施加一个500 kN·m扭矩。先在齿根处建立只含一条裂纹的三维模型，如图4所示，裂纹1在齿根处坐标为(14.8，100，-133.8) mm，设椭圆形裂纹长半轴与短半轴都为0.5 mm。然后再创建如图4(b)所示的双裂纹模型，第一组双裂纹为裂纹1和裂纹2，对应坐标为(14.8，100，-133.8) mm、(14.8，95，-133.8) mm；第二组双裂纹为裂纹1和裂纹3，对应坐标为(14.8，100，-133.8) mm、(14.8，90，-133.8) mm；第三组双裂纹为裂纹1和裂纹4，对应标坐标为(14.8，100，-133.8) mm、(14.8，85，-133.8) mm。建立椭圆形裂纹，设其短半轴与长半轴都为0.5 mm。如图4所示裂纹各个组裂纹分部的距离分别为5、10、15 mm，位置具体分布如图4(b)所示。图4(a)中裂纹1与图4(b)中的裂纹1为初始参数完全相同的裂纹。

图4 齿根裂纹位置

3 齿根双裂纹应力强度因子及疲劳扩展寿命计算与分析

控制单裂纹与双裂纹扩展时，取0～15步的步长为0.09 mm，16～30步的步长0.2 mm，相距5 mm的双裂纹在扩展融合前共扩展了15步，相距10 mm的双裂纹在扩展融合前共扩展了21步，相距15 mm的双裂纹在扩展融合前共扩展了28步。分别计算3种双裂纹不同扩展步的前缘裂纹应力强度因子及裂纹扩展疲劳寿命循环次数。

3.1 应力强度因子的变化规律

直齿轮的应力强度因子主要是型。为探究直齿轮齿根裂纹前缘型应力强度因子的变化规律，需要通过有限元分析计算出上述一组单裂纹及3组双裂纹中裂纹1的数据，然后进行数据处理与分析。初始设置时保证双裂纹模型中裂纹1与单裂纹模型初始参数一样。

根据上述设置的步长，相距5 mm的双裂纹在Franc 3D软件中计算到第15步后自动停止，再扩展就需要扩展融合，则取其单裂纹与双裂纹中裂纹1的初始裂纹(第0步)、第5步、第10步和第15步的裂纹前缘应力强度因子，如图5所示。可以看出：在不同扩展步下的应力强度因子有着一定的变化规律；初始裂纹及扩展的第5步时的单裂纹模型比双裂纹的应力强度因子大，扩展到第10步时前缘的应力强度因子基本相同，扩展到第15步时，整体上单裂纹比双裂纹前缘应力强度因子小，而且裂纹前缘应力强度因子曲线有着两端高中间低的变化趋势，在10步之前两端基本一样，但第15步时双裂纹中的裂纹1右端应力强度因子明显偏高。

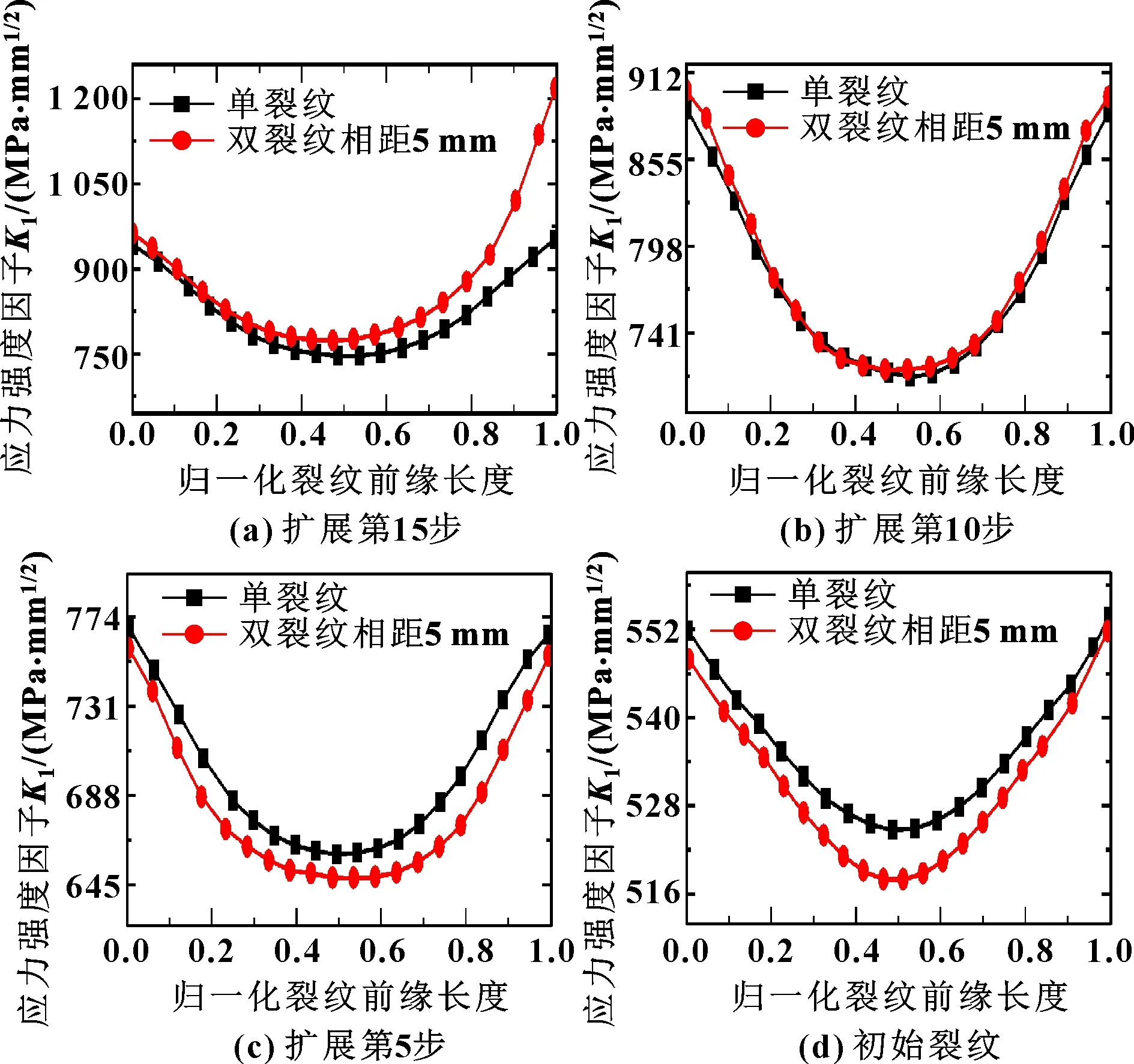
图5 相距5 mm双裂纹中裂纹1与单裂纹在不同扩展步裂纹前缘长度下的应力强度因子

相距10 mm的双裂纹扩展21步后自动停止，为探究不同步长下的应力强度因子的变化规律，取第5、10、15、20步的前缘应力强度进行对比，如图6所示。

图6 相距10 mm双裂纹中裂纹1与单裂纹在不同扩展步的裂纹前缘长度的应力强度因子

由图6可以看出：第5、10步单裂纹比双裂纹模型中裂纹1的前缘应力强度因子大，第15步时基本相等，到第20步时，单裂纹比双裂纹模型中裂纹1的前缘应力强度因子小；整体上看，裂纹前缘应力强度因子曲线有着两端高中间低的变化趋势，在第15步之前两端基本一样，但第20步时双裂纹中的裂纹1右端应力强度因子明显偏高。

相距15 mm的双裂纹扩展到28步后自动停止，取第7、14、21、28步的前缘应力强度因子进行对比，如图7所示。可以看出：第7步单裂纹比双裂纹模型中裂纹1的前缘应力强度因子大，第14步时基本相等，但第21与第28步时，单裂纹比双裂纹模型中裂纹1的前缘应力强度因子小；在扩展到第28步时，单裂纹比双裂纹中裂纹1的前缘应力强度因子要高；整体来看，裂纹前缘应力强度因子曲线有着两端高中间低的变化趋势，在第21步之前两端基本一样，但第28步时双裂纹中的裂纹1右端应力强度因子明显偏高。

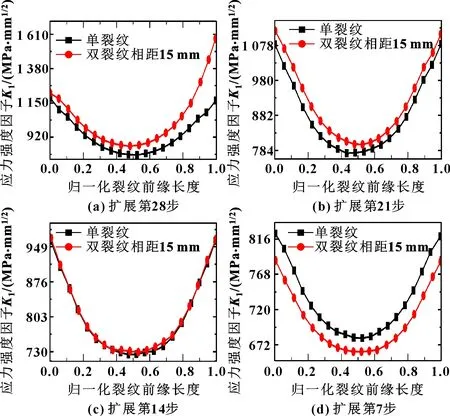
图7 相距15 mm双裂纹中裂纹1与单裂纹在不同扩展步的裂纹前缘长度的应力强度因子

3.2 扩展寿命的变化规律

为探究不同位置双裂纹中裂纹1扩展与单裂纹扩展疲劳寿命的变化规律，在Franc 3D软件中设置基本扩展理论公式为Paris公式，由机械材料手册可得42CrMn的基本断裂参数为：裂纹扩展门槛值Δ=12 MPa·m，=2.318，=1.06×10，断裂临界值=54 MPa·m。通过有限元软件模拟仿真分别得出：单裂纹及相距5、10、15 mm双裂纹中裂纹1扩展疲劳循环次数。

相距5 mm的双裂纹扩展了15步，为探究不同距离的双裂纹中裂纹1与单裂纹在相同扩展步下的疲劳循环次数的变化，设每3步提取一组数据，统计单裂纹及双裂纹中裂纹1疲劳扩展次数并计算出它们的差值，结果如表1所示。

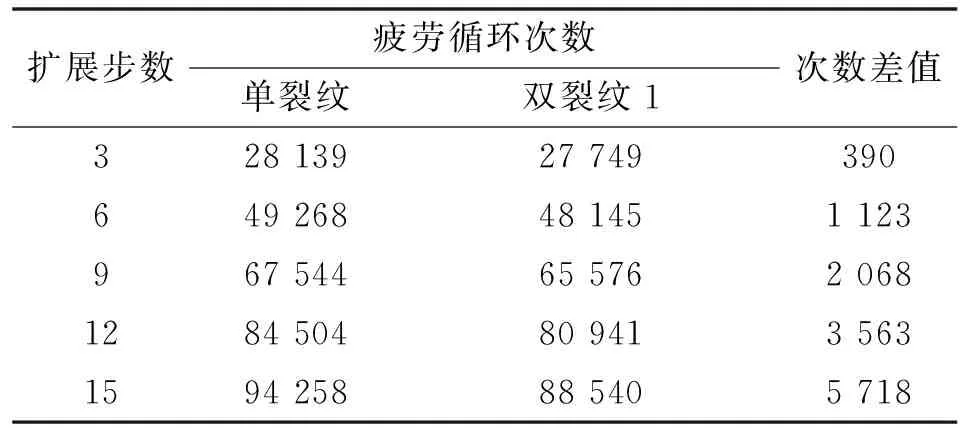
表1 相距5 mm双裂纹中裂纹1与单裂纹在不同扩展步下的疲劳循环次数

相距10 mm的双裂纹扩展了21步，为与相距5 mm双裂纹保持一致，同样设每3步提取一组数据，整理单裂纹及双裂纹中裂纹1疲劳扩展次数并计算出它们的差值，结果如表2所示。

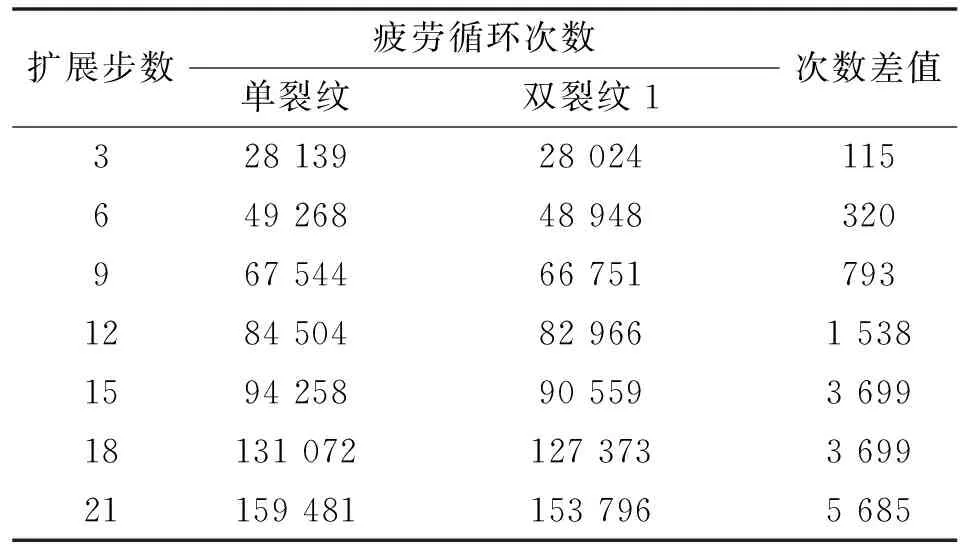
表2 相距10 mm双裂纹中裂纹1与单裂纹在不同扩展步的疲劳循环次数

相距15 mm的双裂纹扩展了28步，为更好地与前面两组数据对比，同样每3步取一组数据，得到表3。

表3 相距15 mm双裂纹中裂纹1与单裂纹在不同扩展步的疲劳循环次数

4 结论

通过有限元软件模拟仿真分析齿根出只含一条裂纹的扩展及在单裂纹基础上改变增加一条裂纹的位置来探究增加的裂纹对单裂纹扩展的影响。

(1)从应力强度因子分析结果可以看出：双裂纹中的裂纹1与单裂纹前缘应力强度因子均呈现中间低两端高的趋势，单裂纹两端基本一样高，而双裂纹中裂纹1的应力强度因子在最后的扩展步都有一个比较明显的上升趋势；整体上看双裂纹中裂纹1刚开始扩展时比单裂纹的应力强度因子小，扩展到最后会高于单裂纹的应力强度因子，中间有一个交替变换的过程。

(2)从拓展寿命结果可以看出：双裂纹中裂纹1疲劳扩展循环次数均小于单裂纹疲劳扩展循环次数，则可以得出产生双裂纹时其中一条裂纹会导致双裂纹中裂纹1的加速扩展，减少寿命周期。

(3)双裂纹相距得越近，相同扩展步下的疲劳循环次数差值越大，说明双裂纹距离越近，双裂纹中裂纹1加速扩展得越快。研究结果为含多裂纹齿轮计算分析及裂纹疲劳扩展寿命预测提供参考。