基于变形离散元法的重力坝地震开裂分析

杨利福， 常晓林， 周　伟， 程勇刚， 马　刚

(武汉大学 水资源与水电工程科学国家重点实验室，武汉　430072)



基于变形离散元法的重力坝地震开裂分析

杨利福， 常晓林， 周伟， 程勇刚， 马刚

(武汉大学 水资源与水电工程科学国家重点实验室，武汉430072)

摘要：考虑脆性材料Ⅰ型和Ⅱ型复合断裂情况，基于渐进破坏理论建立了混凝土损伤破坏模型，提出一种损伤开裂模型与变形离散单元法耦合的分析法。模拟了Koyna坝在强烈地震作用下的渐进破坏过程，通过与室内模型试验及其他方法所得结果的对比，验证了该方法的可靠性和正确性。研究表明：坝体初始裂缝是由地震拉应力集中所致，坝体开裂后，裂缝周围应力重新分布，但缝端仍存在拉应力集中现象，导致裂缝不断扩张；裂缝发展可分4个阶段；裂缝贯通后;坝头与底部剧烈错动;坝体动能减小;摩擦功急剧增加。

关键词：重力坝；地震开裂；变形离散元法；分离裂缝模型

近年来在我国西南地震断裂带附近地区已建、在建或设计了一大批高混凝土重力坝(龙滩、金安桥、观音岩等)，其中许多枢纽坝高达到了200～300 m级，创造了同类型坝的世界最高纪录。西南地区地震烈度多在Ⅷ～Ⅸ度之间(如金安桥水电站设计地震加速度已达0.399 g)，由于坝高、库大，一旦遭遇超强震而溃决失事，不仅会造成重大经济损失，而且对下游所形成的次生灾害将造成难以估量的人民生命财产损失。

目前，研究混凝土重力坝在强震作用下渐进破坏过程的方法主要有模型试验和数值计算等方法。朱彤等[1-2]对混凝土仿真材料特性进行了试验研究，并研究了龙滩水电站碾压混凝土重力坝在地震载荷作用下的破坏特性；李弋等[3]经一系列配合比和力学性能试验及动弹性模量超声波检测，研制出新型高混凝土坝动力试验模型材料；范书立等[4]采用仿真混凝土材料研究了龙开口水电站溢流坝段在不同因素影响下的动力破坏特征和机理；文献[5]通过室内动力模型试验系统研究了Koyna坝和Pine Flat坝在地震作用下的非线性响应；Tinawi等[6]通过一个3.4 m高的混凝土坝模型振动台试验和数值模拟研究了重力坝裂缝扩展和坝体滑移机制。模型试验在一定程度上能够反映混凝土重力坝的破坏过程和规律，但是模型试验采用不同材料可能导致不同的破坏模式，载荷和边界条件难以同时满足相似律要求，试验结果也难以与实际情况一致，并且由于试验观测手段的限制，模型试验无法全面揭示重力坝地震开裂破坏机理。

目前，混凝土重力坝地震响应数值分析主流方法还是有限单元法。在传统有限单元法基础上，文献[7]采用分离裂缝模型、文献[8-9]采用弥散裂缝模型、文献[10-11]采用扩展有限单元法研究了重力坝在地震过程中的非线性响应和失效模式。然而，分离裂缝模型需要预设裂纹发展路径，计算过程中需要重剖分计算网格；弥散裂缝模型通过本构模型反映材料开裂后的性能退化，但要求裂缝单元边界一致，才能得到较精确的结果；扩展有限元计算结果对网格存在依赖性，上述不同的裂缝处理方法所计算的结果也不一致。也有学者在有限单元法的基础上引入裂缝带模型[12]、非线性断裂力学模型[13]、同轴旋转开裂模型[14]、界面单元[15]等研究混凝土重力坝开裂，但是由于有限单元法小位移的限制使得系统由连续介质完全变为非连续介质(坝体裂缝贯通)后的力学行为难以模拟。此外，Das等[16]采用光滑粒子流体动力学方法(Smoothed particle hydrodynamics, SPH)研究了地震载荷作用下的大坝失效过程，但SPH法要求粒子规则排列，对于大变形和冲击载荷问题，其计算结果并不稳定。刘君等[17]应用非连续变形分析(Discontinuous Deformation Analysis,DDA) 和有限单元法(Finite Element Method,FEM)耦合方法研究了碾压混凝土重力坝的动力响应，但该模型尚未考虑混凝土开裂破坏；侯艳丽等[18]采用分离式裂缝模型与离散元耦合的方法模拟了Koyna坝在地震作用下的破坏过程，该方法需要在可能产生断裂的结构部位预设虚拟裂缝，但其破坏模式受预设裂缝位置的影响。

变形离散单元法允许块体发生大变形及旋转，能够很好地模拟块体的脱开和滑移，为分析强震作用下重力坝开裂过程及裂缝贯通后的力学响应提供了一个新方法。因此，本文考虑脆性材料Ⅰ型和Ⅱ型复合断裂情况，基于材料断裂过程区理论建立了混凝土开裂模型，将其嵌入到离散单元法中，提出一种基于变形离散元法的混凝土损伤开裂模型，将该模型应用于Koyna混凝土重力坝在强震作用下破坏过程分析，研究了其由连续介质向非连续系统转换过程以及非连续介质系统的地震响应，得到Koyna坝动力渐进破坏过程、破坏形态以及裂缝贯通后非线性响应，验证了该模型在混凝土重力坝地震破坏分析应用的适用性。

1混凝土损伤开裂模型

变形离散单元法将许多块体组装在一起，引入开裂准则后，可以视其为一个连续的块体，即当块体接触面应力状态满足一定条件时，块体开裂，连续介质向非连续介质转变，这种方法的本质也属于分离裂缝模型，但是离散单元法允许系统发生大位移、转动甚至分离，只要引入合适的开裂破坏准则，就能很好的反映连续介质向非连续介质转变的过程。Kazerani[19-20]基于变形离散单元法研究了火成岩、沉积岩、砂岩在巴西圆盘试验和单轴压缩试验下的细观破坏机理，并将破坏形态与物理试验比对，发现数值试验与物理试验结果非常吻合，验证了该方法在脆性材料开裂研究中的有效性。

分离式裂缝模型将脆性材料的带状微裂区简化为一条分离的裂缝，并假定断裂过程区外的材料仍为弹性变形区。当断裂过程区的尖端应力超过抗拉强度后，过程区向前发展，当外界所做功等于断裂能时，材料完全开裂破坏。只考虑Ⅰ型和Ⅱ型复合断裂情况，定义等效位移后，则断裂能为：

(1)

(2)

式中：δeff为等效位移；δs为切向位移,δn为法向位移，以拉为正；E为材料的弹性模量；KΙC、KΙΙC分别为材料Ⅰ型、Ⅱ型断裂韧度；Gf为断裂能。

断裂过程区理论认为：当不考虑块体内部损伤时，界面刚度应反映开裂破坏区域材料的劣化。在峰值强度前，假设材料处于弹性阶段，处于破坏过程区的接触面法向和切向刚度应该反映局部材料变形特性的劣化，此时，界面上的应力与位移关系是非线性弹性的，即加卸载曲线重合。在峰值强度之后，材料进入损伤阶段，界面的承载力降低 ，刚度逐渐下降，当刚度≃0时，界面完全失效，材料由连续介质转变为非连续介质(见图1)。本文采用Mohr-Coulomb准则作为开裂破坏准则，当界面的法向应力达到抗拉强度后发生拉伸破坏，当界面的切向应力超过抗剪强度则相接触的块体发生滑移。采用指数形式来描述峰值强度前的刚度劣化，则界面的法向和切向应力-位移关系有：

(3)

(4)

式中：kt、ks为法向和切向初始接触刚度系数；δct为峰值应力对应的位移；σn、σs分别为法向和切向应力；σt为材料的抗拉强度；δut为材料完全断裂时的位移；D为损伤因子;kred为残余刚度系数；σsmax=knδntan(φ)+c;φ为接触面内摩擦角;c为黏聚力。

图1　拉应力-位移关系曲线Fig. 1 Stress-displacement curve

因此，断裂能可以表示为：

(5)

变形离散单元法采用动态松弛法对控制方程进行显式时间积分[21]，系统的动能可以表示为：

(6)

当界面上的切向应力σs大于抗剪强度σsmax时，块体滑移错动并产生摩擦功[22]：

(7)

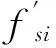
2数值模型与计算参数

印度Koyna坝是混凝土坝动力分析的经典问题，它是少数几个经历强震并具有较完整记录的受震害的混凝土坝工程，因此本文以Koyna坝作为计算模型，并以同幅实测地震动作为输入条件。在该地震中，Koyna坝在91.75 m深的水推力和0.474 g与0.312 g的水平与竖向加速度峰值地震作用下，在多个非溢流坝段，于下游坝高66.5 m和上游坝高60.0～66.5 m处发生了水平裂缝，并在这些裂缝位置发现了渗漏，说明裂缝已经完全贯穿坝体。为了与现有研究成果对比，验证本文所提方法的可行性，本文模型尺寸与计算参数与文献[23]相同。块体划分时，在实际坝体开裂区域周围(坝高51.5～70.5 m)加密，模型尺寸(见图2)，计算参数见表1。

对于普通混凝土，传递应力=0时，对应的位移δut≈0.05 mm，对于高强混凝土δut可达0.08 mm，本文取δut=0.055 mm，混凝土拉应力超过材料强度后，其强度损伤因子按照图3所示规律演化。本文在计算时，变形块体内部划分有限差分单元后采用弹性材料模拟，块体间的接触特性采用混凝土渐进破坏模型；采用Westergaard附加质量考虑动水压力效应；动力计算采用Rayleigh阻尼，阻尼比=0.05，坝体开裂后，坝体振型及固有频率将改变，为了保证解的稳定性，本文采用文献[21]推荐的方法，即将自振频率提高2倍而不考虑刚度阻尼；输入的顺河向和竖向的近坝基位置实测加速度地震记录(见图4)，动力计算中在坝底输入经积分后的速度波。

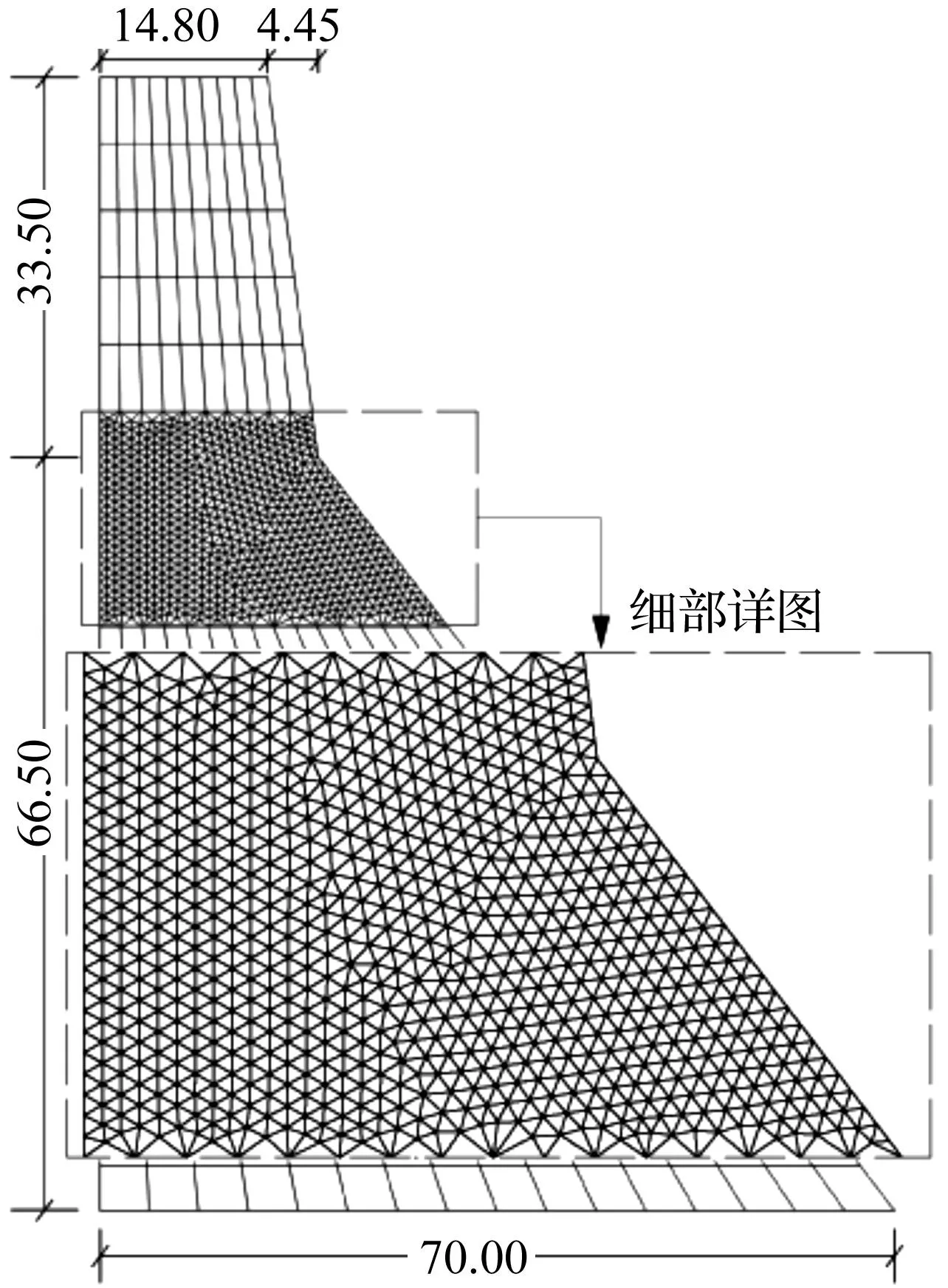
图2　离散元计算块体模型(单位：m)Fig.2 Discrete element model(Unit: m)

图3　损伤因子演化曲线Fig.3 Damage development curve

密度/(kg·m-3)弹性模量/GPa泊松比摩擦系数抗拉强度/MPa粘聚力/MPa2643.031.030.201.202.903.00

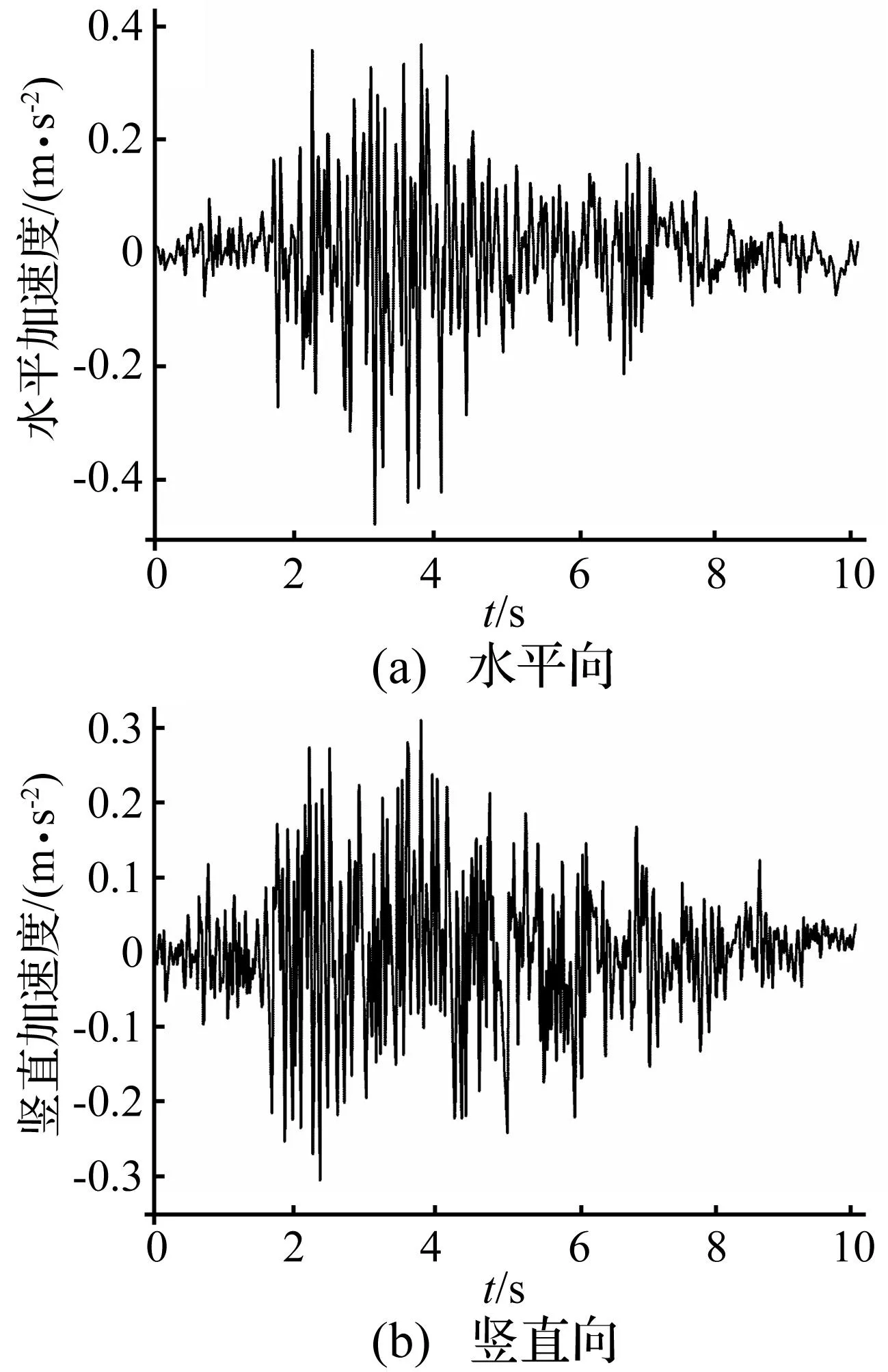
图4　地震加速度记录曲线Fig.4 Acceleration of Koyna earthquake time histories

图5　混凝土单轴拉伸下的应力-位移曲线Fig.5 Stress-displacement curve of concrete under uniaxial tension

图6　不同方法计算结果破坏形态比较Fig.6 Failure mode comparison withdifferent methods

3数值模拟

3.1程序验证

为检验所提混凝土损伤开裂模型与变形离散元法耦合分析方法的可靠性及合理性，本文在商业离散元软件UDEC平台上通过fish语言将式(1)～式(4)编制成相应程序，采用混凝土单轴拉伸试验对程序进行了验证。由图5可知,单轴拉伸下的应力位移曲线数值解与理论值基本一致，说明本文所提计算方法能够模拟混凝土开裂，计算结果可靠。

文献[5]给出了Koyna大坝振动台模型试验得到的强震破坏模式，文献[14]采用同轴旋转开裂模型、文献[23]采用塑性损伤模型给出了Koyna大坝失效模式，见图6。从图6可知,本文计算的坝体破坏模式与其他数值方法计算的坝体失效模式基本一致，与模型试验结果很接近, 说明采用本文所提方法模拟混凝土重力坝地震开裂破坏是可行的。本文模拟得到的最终破坏形态呈“Y”字形：下游折坡处裂缝与坡面基本成90°，裂缝向底部并向上游扩展后出现一个拐点，在此之后裂缝水平向上游扩展，最终形成贯穿性裂缝。

3.2开裂过程分析

图7给出了Koyna地震波作用下的大坝开裂扩展过程。由图7可知，大坝从初始裂纹产生到裂缝贯通历时0.23 s，破坏主要分4个阶段。① 下游折坡处裂缝倾斜扩展阶段：T>4.31 s 时，在坝体下游折坡处首先出现裂缝，裂缝呈约45°(与坡面呈90°)向下部扩展至水平宽度约1/3坝颈宽后，出现一个拐点；② 中部裂缝向下弯曲扩展阶段：在裂缝拐点出现之后，裂缝向下弯曲扩展1/3坝颈宽度；③ 底部裂缝水平扩展阶段：T>4.39 s 时，裂缝大致呈水平向向上游面扩展1/3坝颈宽度；④ 中部裂缝水平扩展贯通阶段：T>4.42 s 时，底部裂缝停止扩展，在上述拐点(裂缝中部)处出现一条向上游扩展的裂缝，该裂缝先斜向上扩展再呈水平向上游扩展，T=4.54 s时，裂缝扩展至上游面，形成上下游贯通的裂缝。

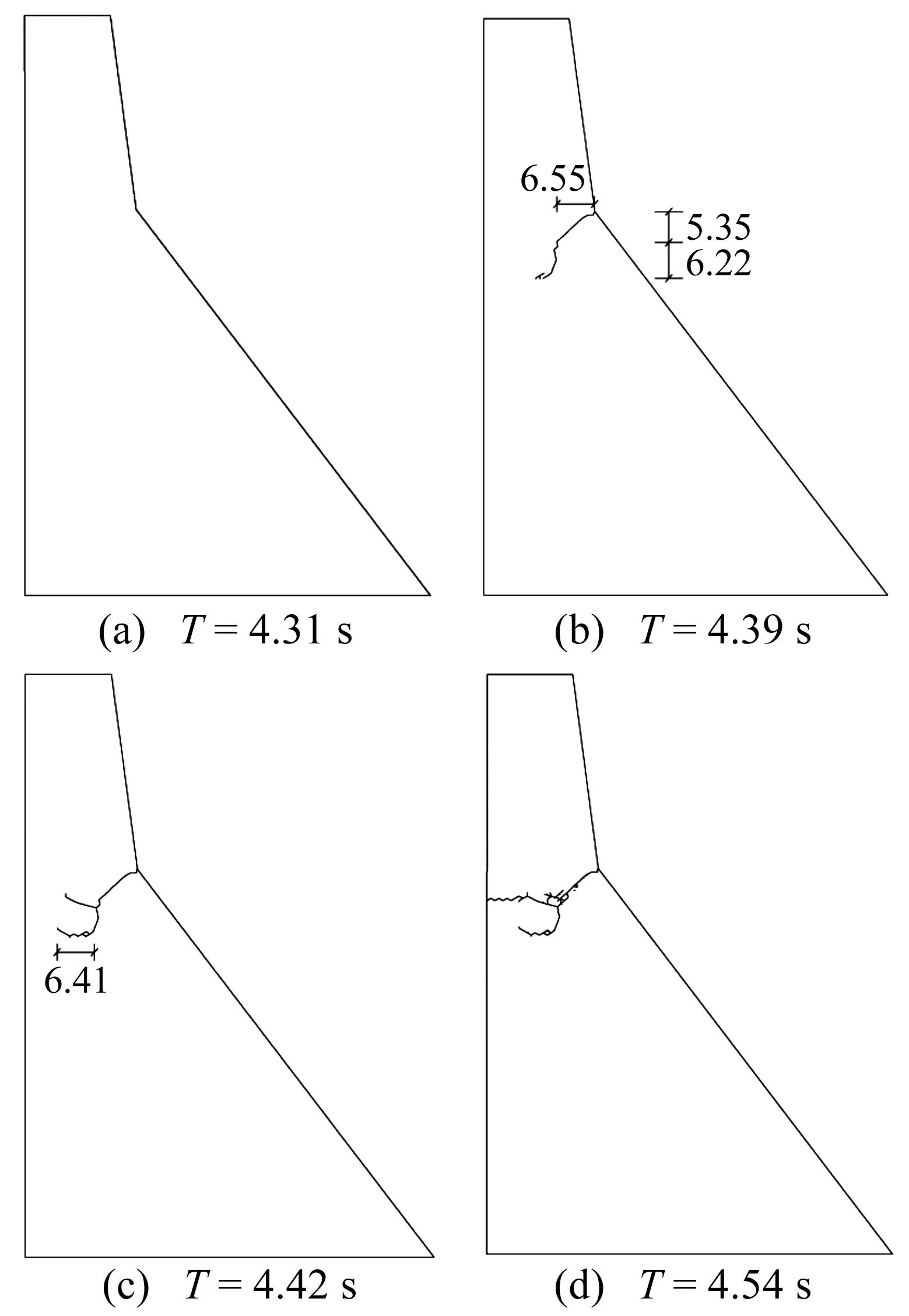
图7　Koyna坝开裂扩展图(单位：m)Fig.7 Crack growth of the Koyna dam(Unit: m)

图8、图9为地震过程中坝体主应力矢量分布图(线段长度表示大小，黑色线条表示受压，灰白色线条表示受拉)从图可知，在开裂前(T=4.31 s)，坝体上游侧主要受压，小主应力(压主应力)平行于竖直向，下游侧受拉，大主应力(拉主应力)平行于下游坡面，折坡处拉应力应力集中现象较为明显，最大拉主应力约3.4 MPa；坝体开裂后(T=4.39 s)，缝端拉应力集中较大，且垂直于裂缝扩展方向，开裂区裂缝周围虽然还存在拉主应力，但是该拉应力方向平行于裂缝方向；T=4.42 s，下游侧裂缝周围的拉应力逐渐转化为压应力；当裂缝贯通后(T=4.54 s)，下游侧裂缝周围拉应力进一步转换为压应力，此时整个坝体应力分布以压为主，最大压应力绝对值达22.0 MPa。对比不同时刻坝体主应力矢量图可知，坝体下游侧在地震作用下，坝体下游折坡处初始裂缝是由拉应力集中导致的，坝体开裂后，裂缝周围应力重分布，但是缝端依然存在拉应力集中现象，导致裂缝不断扩展，最终形成贯穿性裂缝。

图8　不同时间坝体主应力矢量图Fig.8 Principal stress vector at different time

图9　不同时间坝体局部主应力矢量图Fig.9 Principal stress vector of the part of dam at different time

3.3开裂后坝体地震响应

图10、图11为开裂面上A点和B点法向和切向相对位移与接触力时间历程图(法向应力以压为正，法向位移张开为正；切向应力与位移符号表示方向)。由图可知，坝体开裂后，位于裂缝处的应力及位移作剧烈变化且向下游滑移，说明坝头与底部剧烈错动，坝体由连续介质系统向非连续介质系统转化后，系统固有振动频率增大[21]。A点最大的张开位移达9.2 mm，B点法向最大张开位移达0.486 mm。由于A点法向张开位移较大，开裂后并未马上闭合，其法向和切向基本不受力；B点开裂后又闭合，法向和切向接触力方向变化频繁，表现出强烈的非线性。图12为坝体系统摩擦功和动能时间历程曲线，图13裂缝贯穿后坝头滑移图，从图12和图13可知，系统动能达到最大值时，坝体裂缝贯通，坝头滑移量最大值达4.8 mm；裂缝贯通后，坝体动能急剧减小，摩擦功急剧增加，说明在裂缝贯通后，坝头与底部剧烈错动，部分动能以摩擦形式耗散，但整个地震过程中未出现坝头倒塌现象。

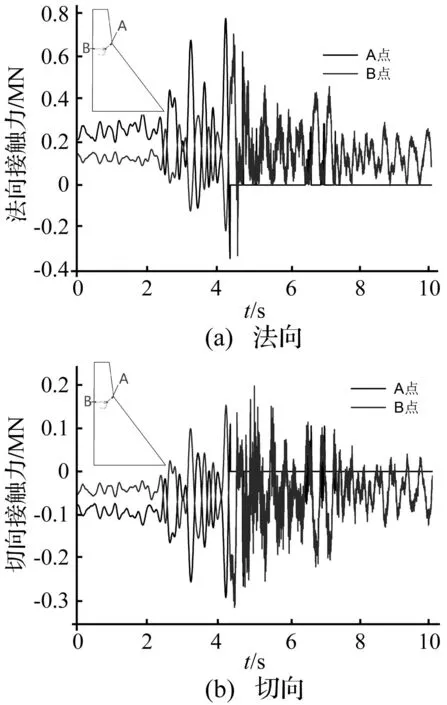
图10　不同位置裂缝的接触力Fig.10 Contact force of crack at different location

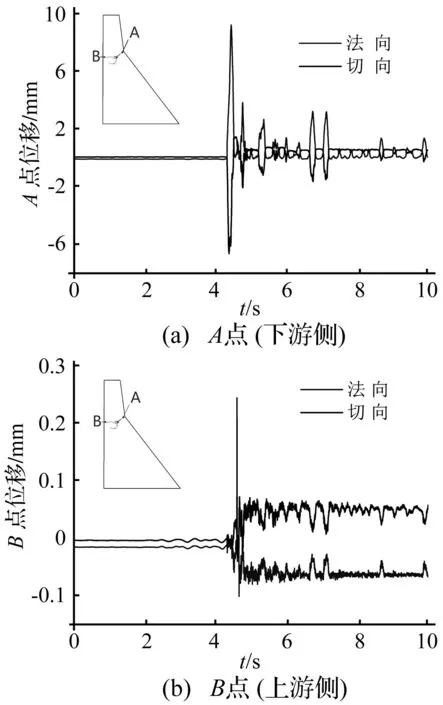
图11　不同位置裂缝的相对位移Fig.11 Relative displacement of crack at different location

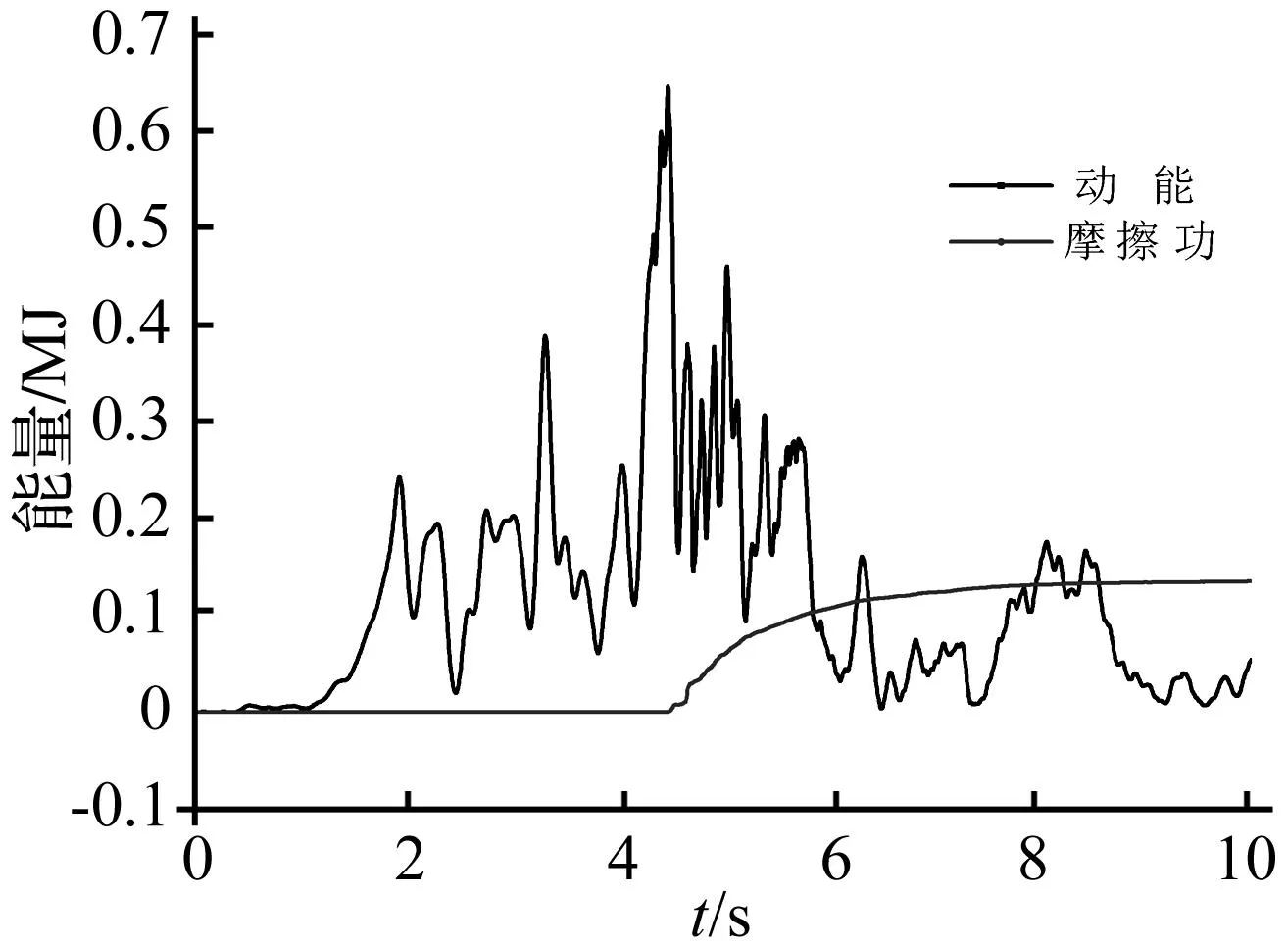
图12　摩擦功和动能时间历程Fig.12 Kinetic energy and friction work time history

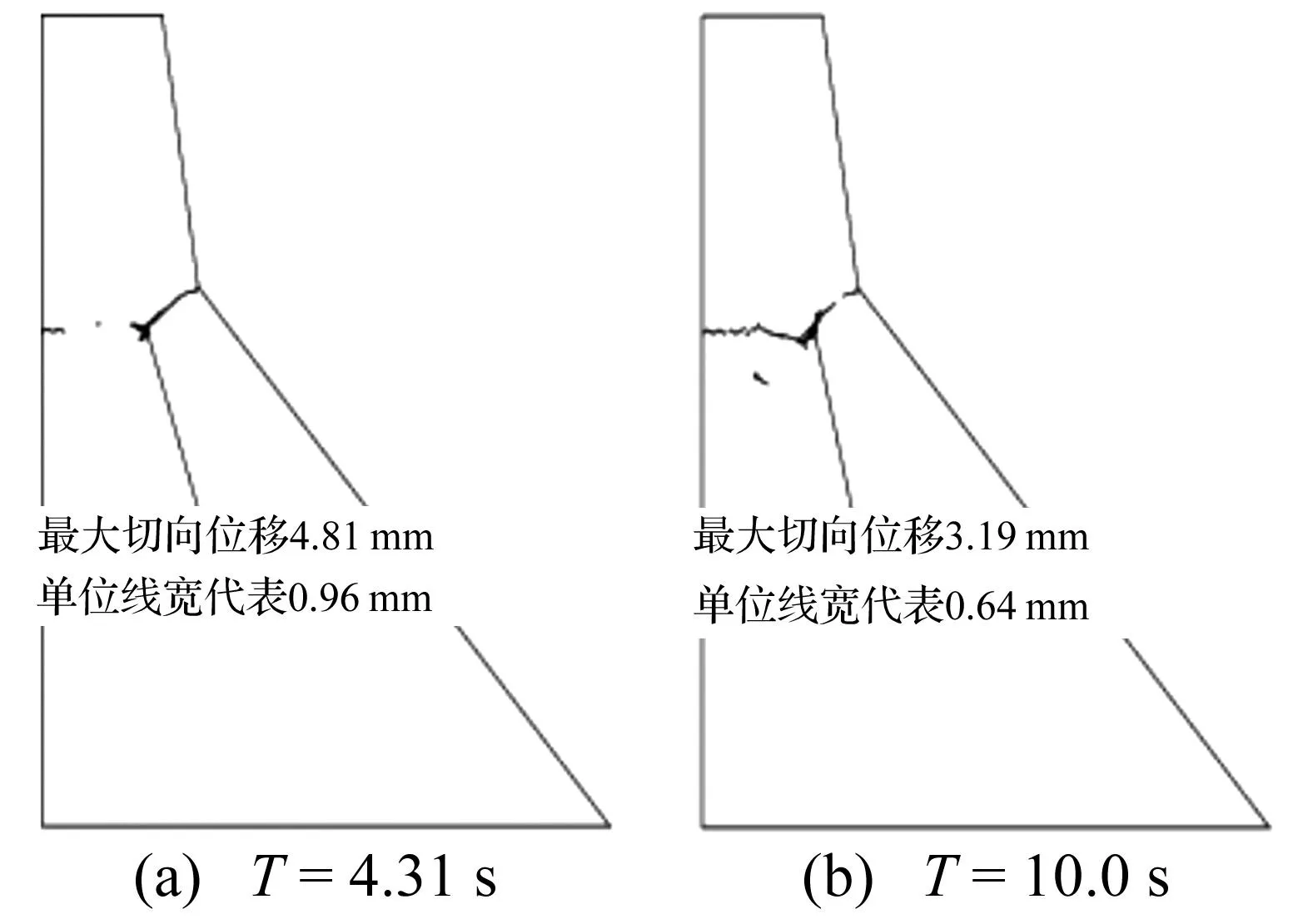
图13　不同时刻坝头滑移图Fig.13 Slip map of dam head at different time

4结论

本文基于脆性材料断裂过程区理论, 考虑Ⅰ型和Ⅱ型复合断裂情况，建立了混凝土损伤破坏模型，提出一种将损伤开裂模型与变形离散元法耦合的分析方法，对Koyna重力坝强震作用下的破坏过程以及坝体开裂后的动力响应进行数值仿真模拟。主要结论如下：

(1) 本文采用变形离散元法与混凝土损伤开裂模型耦合分析方法模拟的Koyna重力坝强震失效模式与模型试验及其他数值方法所得结果一致，说明该方法用于模拟混凝土重力坝地震开裂破坏是可行的。

(2) 下游折坡处初始裂缝是由于地震拉应力集中所致，坝体开裂后，裂缝周围应力重新分布，但缝端仍存在拉应力集中现象，导致裂缝不断扩张，最终形成贯穿性裂缝。

(3) 在强震载荷作用下，Koyna混凝土重力坝的裂缝发展可以分4个阶段：下游折坡处裂缝倾斜扩展阶段，中部裂缝向下弯曲扩展阶段，底部裂缝水平扩展阶段，中部裂缝水平扩展贯通阶段。

(4) 变形离散单元法能够很好模拟坝体裂缝贯通后非连续介质系统的力学响应，裂缝贯通后，系统固有振动频率增大，下游侧裂缝基本不受力，上游侧裂缝接触面在法向上只受压力作用，切向力方向变化频繁，坝头与底部剧烈错动，坝体动能急剧减小，摩擦功急剧增加，但坝头未倒塌。

参 考 文 献

[ 1 ] 朱彤, 林皋, 马恒春. 混凝土仿真材料特性及其应用的试验研究[J]. 水力发电学报, 2004, 23(4): 31-37.

ZHU Tong, LIN Gao, MA Heng-chun. The test research on properties and applications of emulation concrete material[J].Journal of Hydroelectric Engineering,2004,23(4):31-37.

[ 2 ] 朱彤, 林皋,马恒春，等. 龙滩大坝的动力模型破坏试验研究[J]. 水电站设计, 1995, 11(2): 48-54.

ZHU Tong, LIN Gao, MA Heng-chun, et al. Failure test research on dynamic model of long tan dam[J]. Design of Hydroelectric Power Station, 1995, 11(2): 48-54.

[ 3 ] 李弋, 张少杰, 徐进, 等. 混凝土高坝动力模型材料的试验研究[J]. 岩土力学, 2011, 32(3): 757-760.

LI Yi, ZHANG Shao-jie, XU Jin,et al.Experimental research on dynamic model material of high concrete dam[J].Rock and Soil Mechanics, 2011, 32(3): 757-760.

[ 4 ] 范书立, 陈健云, 周晶, 等. 龙开口水电站溢流坝段动力模型破坏试验研究[J].水利学报,2008(增刊1):195-199.

FAN Shu-li, CHEN Jian-yun, ZHOU Jing,et al.Experimental research on over fall sect ion dynamic rupture of longkaikou project[J]. Journal of Hydraulic Engineering, 2008 (Sup1):195-199.

[ 5 ] Panel on earthquake engineering for concrete dams, committee on earthquake engineering. Earthquake engineering for concrete dams: design, performance, and research needs[M]. National Academy Press: 1990.

[ 6 ] Tinawi R, Léger P, Leclerc M, et al. Seismic safety of gravity dams: from shake table experiments to numerical analyses[J].Journal of Structural Engineering,2000,126(4):518-529.

[ 7 ] Mirzabozorg H, Ghaemian M. Non-linear behavior of mass concrete in three-dimensional problems using a smeared crack approach[J]. Earthquake Engineering & Structural Dynamics, 2005, 34(3): 247-269.

[ 8 ] 沈怀至, 周元德, 王进廷. 基于弥散裂缝模型的重力坝简化地震分析[J]. 水利学报, 2007, 38(10): 1221-1227.

SHEN Huai-zhi, ZHOU Yuan-de, WANG Jin-ting.Simplified earthquake analysis of concrete gravity dams using smeared crack approach[J].Journal of Hydraulic Engineering, 2007, 38(10): 1221-1227.

[ 9 ] Valamanesh V, Estekanchi H E, Vafai A, et al. Application of the endurance time method in seismic analysis of concrete gravity dams[J]. Scientia Iranica, 2011, 18(3): 326-337.

[10] 方修君, 金峰, 王进廷. 基于扩展有限元法的 Koyna 重力坝地震开裂过程模拟[J]. 清华大学学报: 自然科学版, 2008, 48(12): 2065-2069.

FANG Xiu-jun，JIN Feng，WANG Jin-ting． Seismic fracture simulation of the Koyna gravity dam using an extended finite element method[J].Tsinghua University:Sci & Tech,2008,48(12): 2065-2069．

[11] 张社荣, 王高辉, 庞博慧, 等. 基于 XFEM 的强震区砼重力坝开裂与配筋抗震措施研究[J]. 振动与冲击, 2013, 32(6): 137-142.

ZHANG She-rong，WANG Gao-hui，PANG Bo-hui, et al. Seismic cracking and reinforcement analysis of concrete gravity dam based on XFEM[J]. Journal of Vibration and Shock, 2013, 32(6): 137-142.

[12] Guanglun W, Pekau O A, Chuhan Z, et al. Seismic fracture analysis of concrete gravity dams based on nonlinear fracture mechanics[J]. Engineering Fracture Mechanics, 2000, 65(1): 67-87.

[13] El-Aidi B, Hall J F. Non-linear earthquake response of concrete gravity dams part 1: Modelling[J]. Earthquake Engineering & Structural Dynamics,1989,18(6):837-851.

[14] Calayir Y, Karaton M. Seismic fracture analysis of concrete gravity dams including dam-reservoir interaction[J]. Computers & Structures, 2005, 83(19): 1595-1606.

[15] 徐海滨, 杜修力, 杨贞军. 基于预插黏性界面单元的 Koyna 重力坝强震破坏过程分析[J]. 振动与冲击, 2014, 33(17): 74-79.

XU Hai-bin，DU Xiu-li，YANG Zhen-jun.Seismic failure analysis of Koyna gravity dam using cohesive interface elements[J]. Journal of Vibration and Shock, 2014, 33(17): 74-79.

[16] Das R, Cleary P W. A mesh-free approach for fracture modelling of gravity dams under earthquake[J].International Journal of Fracture, 2013, 179(1/2): 9-33.

[17] 刘君, 陈健云, 孔宪京, 等. 基于 DDA 和 FEM 耦合方法的碾压混凝土坝抗震安全性分析[J]. 大连理工大学学报, 2004, 43(6): 793-798.

LIU Jun,CHEN Jian-yun, KONG Xian-jing, et al. Seismic stability analysis of rol led compacted concrete dam based on approach of DDA coupled with FEM[J].Journal of Dalian University of Technology, 2004, 43(6): 793-798.

[18] 侯艳丽.砼坝-地基破坏的离散元方法与断裂力学的耦合模型研究[D]. 北京:清华大学, 2005.

[19] Kazerani T. Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock[J].International Journal of Rock Mechanics and Mining Sciences, 2013, 64: 44-55.

[20] Kazerani T, Yang Z Y, Zhao J. A discrete element model forpredicting shear strength and degradation of rock joint by using compressive and tensile test data[J]. Rock Mechanics and Rock Engineering, 2012, 45(5): 695-709.

[21] 王泳嘉, 邢纪波. 离散单元法及其在岩土力学中的应用[M]. 沈阳: 东北工学院出版社, 1991.

[22] UDEC (Universal Distinct Element Code) user’s manual[M]. Version 4.01, Itasca Consulting Group. Inc., 2008.

[23] Dassult Systems Inc. ABAQUS Standard User’s manual[M]. Version 6.11.1, 2011.

Seismic cracking analysis of a gravity dam based on deformable distinct element method

YANGLi-fu,CHANGXiao-lin,ZHOUWei,CHENGYong-gang,MAGang(State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

Abstract:Considering brittle materials’ mode-I and mode-II mixed fracture, a concrete damage failure model was established based on the progressive failure theory. An analysis method considering the coupling between the model and the deformable distinct element method was proposed. The progressive failure process of Koyna dam under the action of strong earthquake was simulated. The reliability and correctness of the proposed method was verified by comparing the simulated results with those of the model tests and other methods. The study results indicated that the initial crack of the dam is caused due to tensile stress concentration induced by earthquake; the dam cracking causes the redistribution of stress but there is a tension stress concentration phenomenon around the crack tip to cause crack expanding; the crack growth can be divided into four phases; after fracture penetration, severe diastrophism happens between the head and bottom of the dam, the dam’s kinetic energy decreases but the friction work dramatically increases.

Key words:gravity dam; seismic fracture; deformable distinct element method; discrete crack model

中图分类号:TU457

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.008

通信作者周伟 男，教授，1975年生

收稿日期：2015-01-04修改稿收到日期：2015-03-06

基金项目：国家自然科学基金资助项目(51179139)

第一作者 杨利福 男，博士生，1987年生