三塔两跨悬索桥行波效应振动台试验及数值研究

闫聚考, 李建中， 彭天波， 王军文

(1.石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室，石家庄　050043；2.同济大学 土木工程防灾国家重点实验室，上海　200092；3.石家庄铁道大学 土木工程学院，石家庄　050043)



三塔两跨悬索桥行波效应振动台试验及数值研究

闫聚考1，2, 李建中2， 彭天波2， 王军文3

(1.石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室，石家庄050043；2.同济大学 土木工程防灾国家重点实验室，上海200092；3.石家庄铁道大学 土木工程学院，石家庄050043)

摘要：为了研究行波效应对大跨多塔连跨悬索结构抗震性能的影响，以泰州长江公路大桥为背景，设计并制作1∶40缩尺比例模型，进行了全桥振动台模型试验。采用中塔与主梁间弹性索连接的纵向约束结构体系，试验分别测试了不同视波速下行波效应对全桥位移响应的影响。振动台试验表明，考虑行波效应时，中塔顶位移、北塔梁纵向相对位移会有明显增大，最大增幅>50%；主桥梁与引桥梁纵向相对位移也会有明显增大，增大幅值>1倍。因此，仅考虑一致地震激励不能保证大跨度多塔悬索桥的结构安全。通过比较试验结果和数值计算结果可知，试验结果与有限元数值模拟结果较接近、吻合较好。数值计算所采用的绝对位移法分析行波效应方法操作简单，力学概念清晰，可方便的应用到大跨度桥梁行波效应分析中。

关键词：三塔两跨悬索桥；行波效应；振动台试验；数值模拟

多塔悬索桥为多支承结构，具有超长的跨度，当地震动经过这样长距离的传播时，不同支承点在同一时刻遭受的地震激励很不相同，地震动的空间变化的影响不容忽视。地震动的空间性效应包括：行波效应、局部场地效应和相干波效应。国内外学者对大跨度桥梁在行波效应下的地震反应进行了一些数值分析的研究。早在1965年Bogdanoff等[1]建立了简化的悬索桥计算模型，对其进行了行波效应分析。Dumanoglu等[2-4]对欧洲三座大跨悬索桥(Humber,Bogazici, Fatih)建立了三维有限元模型，用不同剪切波速，纵向，横向输入下进行了地震反应分析。Abdel-Ghaffa等[5-6]利用实际的地震记录，在时域和频域内对金门大桥进行了竖向和横向输入下的地震反应分析。胡世德等[7]利用自编程序对江阴长江公路大桥进行了考虑行波效应的地震反应分析。关于行波效应的振动台全桥试验还很少，然而试验研究在土木工程领域有着重要的意义。Saiidi等[8]在内华达大学里诺分校进行了缩尺比为1∶4的四跨连续梁全桥试验，试验中采用了三个独立的振动台。杨澄宇[9]在香港科技大学，以一座斜拉桥为背景，进行了缩尺比为1∶150的全桥振动台试验，试验中用到两个振动台，研究了非一致输入的影响。这些研究结果表明，一致激励并不能代表最不利的地震输入，在对大跨悬索桥进行地震反应分析时不能忽略行波效应的影响。

鉴此，本文在大比例泰州长江公路大桥全桥振动台试验[10]的基础上，利用有限元软件SAP2000在多个试验工况下行波效应对大跨三塔两跨悬索桥的影响，将试验与计算结果进行对比分析。

1振动台试验模型简介

1.1试验模型

泰州长江公路大桥主缆的分跨为390 m+1 080 m+1 080 m+390 m，振动台允许的模型最大尺寸为70 m。考虑振动台面尺寸及承载能力等条件，平面几何尺寸在振动台工作范围之内，立面高度满足试验室制作场地高度要求以及模型吊装行车的高度要求，因此确定几何尺寸比例为1∶40，主要相似关系见表1，试验模型在振动台上的布置如图1。对模型进行截面设计时，若严格按相似比设计构件截面将无法制作，因此采用刚度等效原则对截面进行简化设计。混凝土塔柱纵筋设计按抗弯能力等效原则、箍筋设计按抗剪能力等效原则进行计算[10]。模型截面尺寸、配重设计及传感器布置等设计过程详见文献[11-13]。

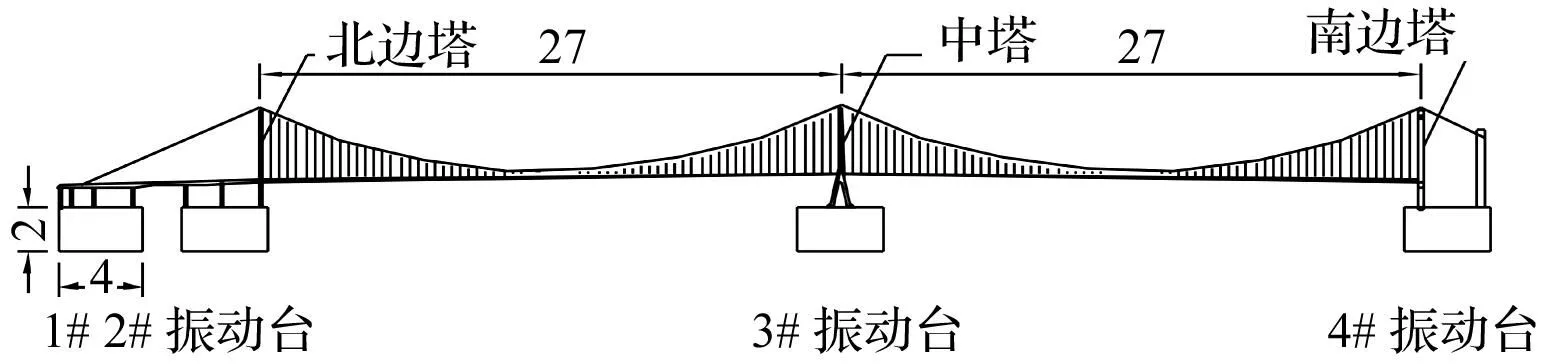
图1　振动台试验模型布置图(单位：m)Fig.1 The test model and arrangement of four shake tables(unit:m)

参数弹性模量长度抗弯惯距力弯矩密度质量频率加速度量纲SESlSl4SESl2SESl3SE/SlSESl2Sl-0.51混凝土构件0.3330.0253.91×10-72.08×10-45.21×10-613.332.08×10-46.3251钢构件10.0251.30×10-72.08×10-45.21×10-613.332.08×10-46.3251

注：其中S为相似系数；SE为弹性模量相似系数；Sl为长度相似系数

图2　振动台试验模型照片Fig.2 Photo of shake table test model

1.2试验工况

泰州长江公路大桥边塔、中塔与主梁之间都安装有横向抗风支座，限制主梁的横向位移。在中塔与主梁之间设置弹性索以限制梁端的纵向位移。本次试验选定一条人工合成地震波(泰州波)和一条实际地震记录(EI Centro波)为振动台台面输入波，按时间相似比压缩后时程曲线(见图3)。表2只列出相关的试验工况，表3列出了四种行进波速及对应原型中的波速，并列出主跨间的延迟时间。试验中考虑地震波的传播方向是由北边塔向南边塔。

2行波效应分析理论

考虑随时间和空间变化的地震动多点激励时，大跨桥梁结构的地震反应分析方法可以分为两大类：① 以地震地面运动为确定过程的确定性分析方法，主要包括反应谱法和时程分析方法；② 以地震地面运动为随机过程的概率性分析方法，主要是指随机振动法。目前大跨桥梁考虑多点激励和行波效应仍多采用确定性的方法。绝对位移法是一种同时考虑多点激励和非线性地震反应的分析方法。对于图4所示的多自由度体系，按结构节点s、基础节点f及结构与基础界面的公共节点c分块,假设Us为结构位移；Uc为公共节点处位移；Uf为基础位移。

表2　行波效应相关试验工况

表3　视波速与延迟时间

注：∞代表视波速无穷大，即一致输入

图3　试验输入地震波Fig.3 Earthquake wave used as the input motion in the tests

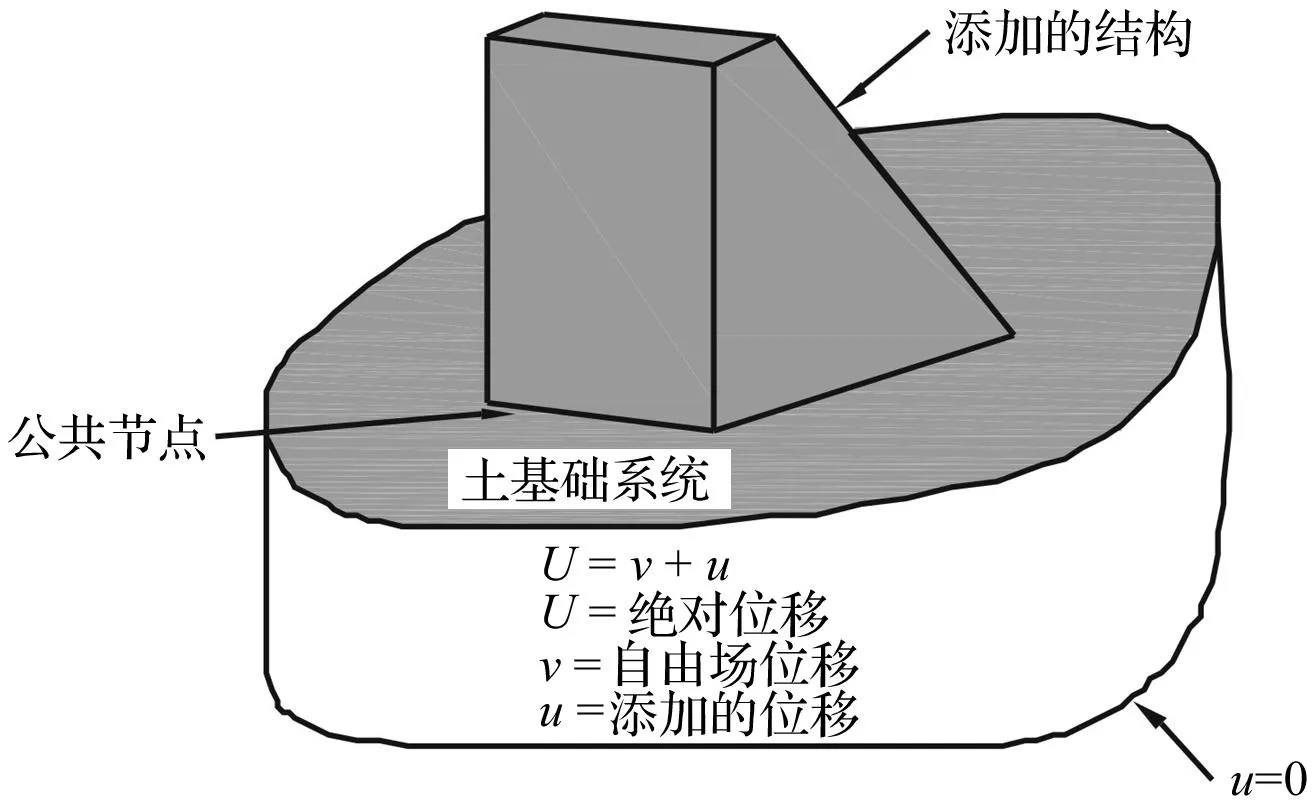
图4　结构和基础组合模型Fig.4 structure and foundation of model

按结构分析中有限元方法的直接刚度法原理，以绝对位移U的形式建立土-结构整个系统的动力平衡方程[14]：

(1)

其中在接触节点的质量和刚度是结构(s)与基础(f)贡献之和，即有下两式：

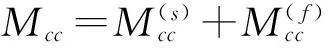
(2)

U可以表示为式(3)，式中:uc结构运动引起的公共节点位移；uf为结构运动引起的基础位移；vc为自由场运动引起的公共节点位移；vf为自由场运动引起的基础位移。

(3)

基础自由场运动要求：

(4)

把式(3)代入式(1)，考虑式(4)自由场响应后, 基础和结构连接采用的是无质量的刚性弹簧，忽略阻尼力。则式(1)可简化为：

(5)

式(5)即为多点非一致输入下的结构动力方程，利用式(5)可求得结构的绝对位移Us。

3试验与计算结果对比

3.1试验结果

表4列出了行波输入下塔顶位移、塔横梁与主梁相对位移和主梁与边梁相对位移的极值比较。从表4可知：EI Centro波行波输入下，北塔顶位移减小，视波速118.5 m/s时减幅最大，达36.1%；中塔顶位移增加，视波速39.5 m/s时增幅最大，达61.5%；北塔梁相对位移则有增有减，视波速79 m/s时增幅最大，达46.1%，视波速158 m/s时，减幅12.5%；中塔梁相对位移减少，视波速158 m/s时减幅最大，达60.3%；主桥梁与引桥梁相对位移明显增大，视波速79 m/s时减幅最大，达121.7%。泰州波行波输入下，北塔顶位移时有增减，视波速118.5 m/s时增幅最大，达19.6%，视波速39.5 m/s时，减幅9.5%；中塔顶位移均有增加，视波速39.5 m/s时增幅最大，达53.5%；北塔梁相对位移时有增减，视波速39.5 m/s时增幅最大，达58.3%，视波速158 m/s时，减幅6%；中塔梁相对位移时有增减，视波速79 m/s时减幅最大，达3.4%，视波速158 m/s时，减幅39.1%；主桥梁与引桥梁相对位移明显增大，视波速39.5 m/s时减幅最大，达104.6%。

由以上分析可知，考虑行波效应时，北塔顶位移变化较小；中塔顶位移、北塔梁相对位移会有明显增大，最大增幅在50%以上；中塔梁相对位移变化较小；主桥梁与引桥梁相对位移会有明显增大，增大幅值>1倍。因此，对大跨度桥梁进行抗震设计时要考虑行波效应对塔梁相对位移的影响，保证支座有足够的位移余量；同时要考虑行波效应对主梁与引桥梁间相对位移的影响，防止相对位移(远离)过大时引起落梁、相对位移(靠近)过小时引起主梁与引桥梁间发生碰撞。

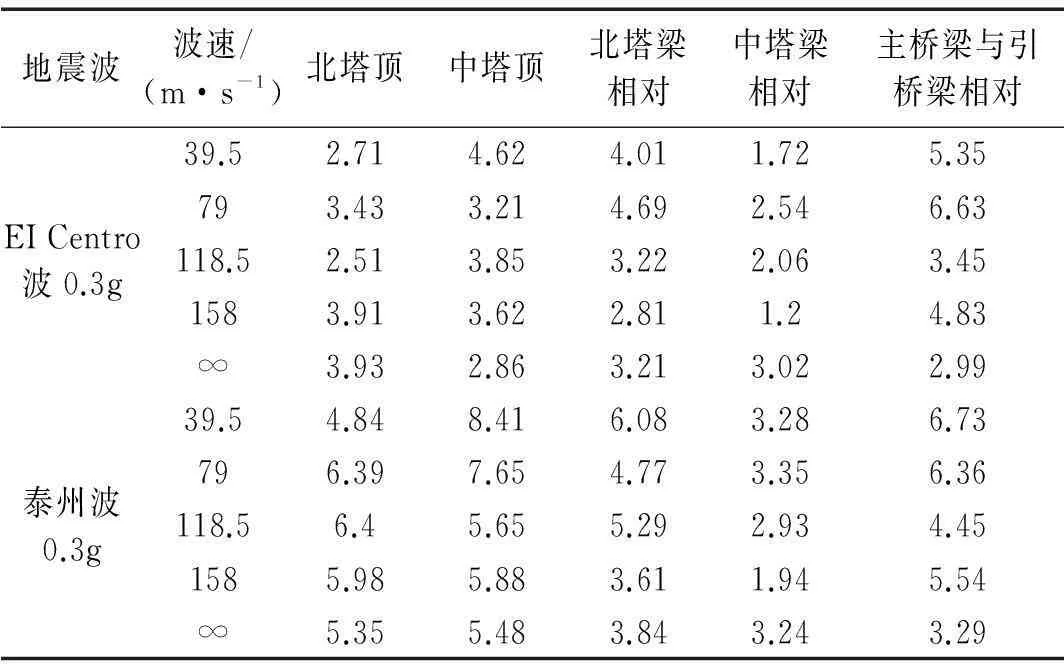
表4　振动台试验纵向位移响应(单位：mm)

3.2数值与试验结果对比

图5～图 8给出了泰州波和EI Centro波输入视波速39.5 m/s和118.5 m/s时，塔横梁与主梁相对位移、主梁与边梁相对位移及边梁与塔横梁相对位移时程曲线的振动台实测值与数值模拟值对比图。数值结果与试验结果间的误差可能原因有两个方面，① 由于模型很大，细部构造及连接较为复杂，试验模型构件间的连接与数值计算时的理论约束存在差异；② 数值计算时采用的阻尼比与模型试验过程中自身的阻尼比存在差异。根据上述图塔、梁间及梁、梁间相对位移的比较结果可知，振动台试验结果与有限元数值模拟结果较接近、吻合较好，说明利用SAP2000有限元程序采用绝对位移法计算行波效应的方法可靠。

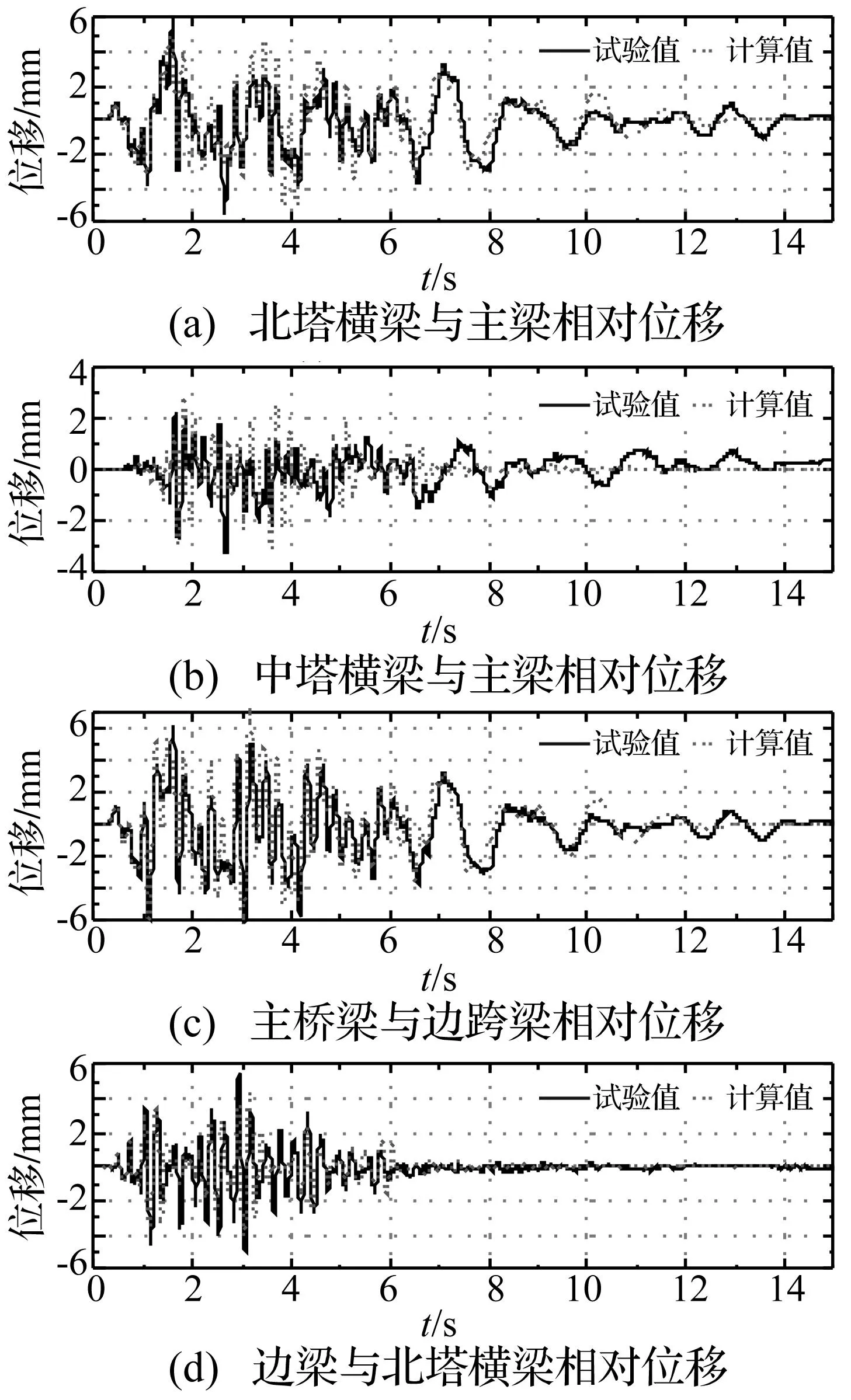
图5　泰州波输入(视波速39.5 m/s)Fig.5 Taizhou wave (wave velocity:39.5 m/s)

图6　泰州波输入(视波速118.5 m/s)Fig.6 Taizhou wave (wave velocity:118.5 m/s)

图7　EI Centro波输入(视波速39.5 m/s)Fig.7 EI Centro wave (wave velocity:39.5 m/s)

图8　EI Centro波输入(视波速118.5 m/s)Fig.8 EI Centro wave (wave velocity:118.5m/s)

4结论

采用振动台试验分析了三塔两跨悬索桥模型的动力响应，通过对四个振动台输入不同速度地震波，研究了考虑行波效应模型的地震位移响应规律，同时采用数值方法模拟了振动台试验的过程，并进行对比验证，得出以下结论:

(1) 振动台试验表明，考虑行波效应时，北塔顶位移和中塔梁相对位移变化较小；中塔顶位移、北塔梁相对位移会有明显增大，最大增幅>50%；主桥梁与引桥梁相对位移也会有明显增大，增大幅值>1倍。因此，在研究塔梁间限位措施及主桥与引桥间相互作用时，必须考虑行波效应对塔梁相对位移及主桥与引桥间相对位移的影响

(2) 通过比较考虑行波效应试验结果和数值计算结果可以发现，试验结果与有限元数值模拟结果较为接近、吻合较好。数值计算所采用的绝对位移法分析行波效应方法操作简单，力学概念清晰，可方便的应用到大跨度桥梁行波分析中。

参 考 文 献

[ 1 ] Bogdanoff J L, Goldberg J E, Schiff A J. The effect of ground transmission time on the response of long structures[J].Bulletin of the Seismological Society of America,1965, 55(3):627-640.

[ 2 ] Dumanoglu A A, Severn R T. Seismic response of modern suspension bridges to asynchronous vertical ground motion[C]//ICE Proceedings. Thomas Telford, 1987, 83(4): 701-730.

[ 3 ] Dumanoglu A A，Severn R T.Seismic response of modern suspension bridges to asynchronous longitudinal and lateral ground motion[C]//ICE Proceedings. Thomas Telford, 1989, 87(1): 73-86.

[ 4 ] Dumanoglu A A, Brownjohn J M W, Severn R T. Seismic analysis of the fatih sultan mehmet (second bosporus) suspension bridge[J]. Earthquake Engineering & Structural Dynamics, 1992,21(10): 881-906.

[ 5 ] Abdel-Ghaffar A M,Stringfellow R G. Response of suspension bridges to travelling earthquake excitations: Part I: vertical response[J].International Journal of Soil Dynamics and Earthquake Engineering,1984,3(3): 62-72.

[ 6 ] Abdel-Ghaffar A M,Stringfellow R G. Response of suspension bridges to travelling earthquake excitations: Part I: lateral response.[J] International Journal of Soil Dynamics and Earthquake Engineering,1984,3(3): 73-81.

[ 7 ] 胡世德,范立础.江阴长江公路大桥纵向地震反应分析[J]．同济大学学报:自然科学版,1994,22(4):433-438.HU Shi-de,FAN Li-chu.The longitudinal earthquake response analysis for the jiangyin yangtze river bridge[J]. Journal of Tongji University:Natural Science Edition,1994,22(4):433-438.

[ 8 ] Saiidi M S, Nelson R, Sadrossadat-Zadeh M, et al. Shake table studies of a 4-span reinforced concrete bridge model[C]// Proceedings 2007 ANCER Meeting, Earthquake Engineering Research: From Strong Seismic Regions to Regions of Moderate Seismicity, HK, China.

[ 9 ] Yang C Y. Seismic analysis of long span bridges including the effects of spatial variation of seismic waves on bridges. Ph. D. thesis[D].Department of Civil Engineering, Hong Kong University of Science and Technology, 2007.

[10] 周颖，吕西林.建筑结构振动台模型试验方法与技术 [M].北京：科学出版社，2012.

[11] Li J, Yan J,Peng T,et al. Shake table studies of seismic structural systems of a taizhou changjiang highway bridge model[J]. 2015，20(3): 04014065.

[12] 闫聚考,李建中,彭天波. 泰州长江公路大桥振动台试验——试验设计及抗震体系试验结果分析.[J].东南大学学报:自然科学版,2014,44(2):357-362.

YAN Ju-kao,LI Jian-zhong,PENG Tian-bo. Shake table test of Taizhou changjiang highway bridge:test design and result analysis of seismic structural system[J].Journal of Southeast University:Natural Science Edition,2014,44(2):357-362.

[13] Yan Ju-kao, Han Lei, Zhao Yi, et al.Scaled down model design of shaking table test of Taizhou Bridge[J]. Engineering Sciences, 2012, 10(3):33-37.

[14] Wilson E L. Three dimensional static and dynamic analysis of structures: a physical approach with emphasis on earthquake engineering[M].Computers and Structures Inc., 1998.

Shake table tests and numerical analysis for traveling wave effect of a three-tower two-span suspension bridge

YANJu-kao1,2,LIJian-zhong2,PENGTian-bo2,WANGJun-wen3(1. Hebei Provincial Key Lab of Structural Health Monitoring and Control, Shijiazhuang Tiedao University,Shijiazhuang 050043,China;2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;3. School of Civil Engineering, Shijiazhuang Tiedao University,Shijiazhuang 050043, China)

Abstract:In order to study traveling wave effect of a long-span multi-tower suspension structure, a 1/40 scale model for Taizhou Changjiang Highway Bridge was designed, constructed and tested on a shaking table. Elastic cables were adopted to connect the main beam and the middle tower. The shake table test method was used to measure the traveling wave effect on the seismic displacement responses of the bridge model under different apparent wave velocities. The test results showed that the structural displacement responses increase remarkably considiering the traveling wave effect, comparing with those under uniform seismic excitation, the top longitudinal displacement of the middle tower and the relative longitudinal displacement between the main beam and the north tower increase more than 50 percent; the relative longitudinal displacement between the main beam and the approach bridge beam increases more than 1 times; therefore, the long-span multi-tower suspension bridge is unsafe only considering uniform seismic excitation. Comparing the results of shaking table tests with those of numerical analysis, it was shown that the test results are close to those of the FE numerical simulation; for the numerical analysis of the traveling wave effect, the absolute displacement method is simpler, its mechanics concepts are very clear; the absolute displacement method can be applied in analyzing the traveling wave effect for long-span bridges.

Key words:three-tower two-span suspension bridge; traveling wave effect; shake table test; numerical analysis

中图分类号:U448.25

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.007

收稿日期：2015-09-01修改稿收到日期：2015-10-13

基金项目：国家科技支撑计划项目资助(2009BAG15B01);973计划项目资助(2013CB036302);国家自然科学基金项目资助(51508347);河北省大型基础设施防灾减灾协同创新中心资助

第一作者 闫聚考 男，博士，讲师，1984年生

E-mail:yanjukao@163.com