全断面开挖爆破产生的自由面对振动频率的影响研究

杨建华， 卢文波， 严　鹏， 姜清辉， 周创兵

(1.南昌大学 建筑工程学院，南昌　330031； 2.武汉大学 水资源与水电工程科学国家重点实验室，武汉　430072)



全断面开挖爆破产生的自由面对振动频率的影响研究

杨建华1， 卢文波2， 严鹏2， 姜清辉1， 周创兵1

(1.南昌大学 建筑工程学院，南昌330031； 2.武汉大学 水资源与水电工程科学国家重点实验室，武汉430072)

摘要：通过对爆破试验中处于不同自由面条件下的炮孔爆破产生的振动信号进行频谱分析，并结合爆破振动数值模拟，研究了地下洞室全断面毫秒延迟爆破过程中产生的自由面对振动频率的影响机理及变化规律。结果表明：爆炸荷载产生的压应力波传播至自由面时发生反射，反射稀疏波与原应力波叠加致使远区荷载压力的上升时间和持续作用时间变短，造成荷载的频率变大，从而导致有自由面条件下其振动频率增大、高频振动能量占总能量的比重增加；爆源与自由面之间的距离越小，爆破振动频率越高；从振动频率的角度来看，较好的自由面条件可以减小爆破振动对结构的破坏。试验监测结果验证了分析结论的可靠性。

关键词：地下洞室；爆破；自由面；振动频率

爆破振动是岩土介质爆破开挖最主要的危害，因爆破振动效应引起的结构变形、开裂和失稳等破坏时有发生，因此在工程爆破中应尽力降低爆破振动对结构的影响，以确保爆破安全。爆破振动特性受爆源因素和传播条件的影响，地下隧洞和井巷全断面毫秒延迟爆破开挖过程中，掏槽孔、崩落孔、缓冲孔和周边孔由里向外依次起爆，掏槽孔是在只有掌子面这一个自由面(临空面)的条件下爆破，前一圈炮孔爆破为后一圈炮孔的爆破创造了新的自由面，其他各圈炮孔均在两个自由面条件下爆破(见图1)。爆破产生的自由面是重要的爆源因素之一，自由面的数量、大小和形态直接影响到爆破破碎效果，同时也对爆破振动具有显著的影响。

国内外学者采用波动理论、现场试验和数值模拟等手段对岩土介质中自由面对爆破振动效应的影响开展研究。一般认为，炸药爆炸产生的能量在自由面方向上快速释放并从自由面反射回稀疏波，从而导致穿过岩体破碎区并以地震波形式传播的能量减少、爆破振动减弱[1]；爆源与自由面之间距离的大小、即抵抗线对振动速度具有显著的影响，振动速度随抵抗线的增加而增大[2]。Singh等[3-4]在露天台阶爆破时的振动监测结果就表明，在自由面较好的条件下，质点峰值振动速度显著降低。国内学者陈星明等[5-7]在现场试验的基础上，得出了随自由面数量的增加，质点峰值振动速度大幅度降低的结论。许海亮等[8]对此提出了包含自由面面积的钻孔爆破振动速度计算公式。但关于自由面数量对质点峰值振速传播衰减速率的影响，不同学者的监测结果还存在较大的争议。

图1　地下洞室全断面毫秒延迟爆破示意图Fig.1 Schema of the full-face millisecond delay blasting in underground openings

然而，Wu等[9]在数值模拟地下爆破时却发现，地表自由面对地震波的反射对爆破振动起放大作用；邓华锋等[10]在隧洞爆破振动监测中也得到了类似的研究结论，并进一步指出质点振动速度具有明显的方向效应，质点朝自由面法向的振动速度明显大于其它方向。Blair等[11]通过对前人的试验数据进行分析并结合自己的现场试验和数值计算研究，认为抵抗线大小对振动速度影响不大，两者之间并没有明显的变化关系；Brent等[12]进行不同抵抗线条件下的单孔爆破试验，也得到了上述相同的结论。而Uysal等[13]通过现场爆破振动监测甚至得出了振动速度随抵抗线的增大而减小的结论。

纵观现有的自由面对爆破振动效应的影响研究，绝大部分研究成果集中在振动强度,即质点峰值振动速度这一指标上;并且对该问题目前也尚无统一的认识。大量的工程实践和理论研究已经表明，将质点峰

值振动速度作为唯一的爆破振动安全判据有较大的局限性和不合理性，采用考虑振动频率影响的爆破振动安全判据是目前国际上爆破安全规范的主流。然而，相比于质点峰值振动速度方面的大量研究成果，国内外对振动频率的研究要少得多，在自由面对振动频率特性的影响研究方面更是鲜有报道，为数不多的研究成果也只是唯象地展示了自由面数量变化对振动频率的影响。因此，迫切需要开展爆破振动频率衰减机制和传播规律的研究，以及自由面对振动频率的影响机理及变化规律研究。

本文研究地下洞室全断面毫秒延迟爆破过程中爆破产生的自由面对振动频率的影响。首先开展小规模爆破试验，比较不同自由面条件下的炮孔爆破激发振动的频谱特性，然后利用数值模拟并结合理论分析讨论自由面对振动频率的影响机理及其变化规律。

1不同自由面条件下爆破振动频率比较

1.1现场试验方案

由图1可知，地下洞室全断面爆破过程中，掏槽孔是在只有掌子面这一个自由面的条件下爆破，而崩落孔是在两个自由面条件下爆破，为了分析爆破产生的自由面对振动频率的影响，试验中比较相同钻孔、装药量的条件下，掏槽孔爆破和崩落孔爆破时的振动频谱特性。受现场试验条件的限制，爆破试验选在某水电站排水洞进水口边坡上进行(排水洞内已衬砌完成，无法在隧洞内进行爆破试验)，将近乎垂直的边坡视作开挖爆破掌子面，在边坡上钻水平炮孔模拟地下洞室全断面开挖爆破的情形(见图2)。试验中全断面开挖分一段掏槽孔和两段崩落孔爆破进行，分别采用MS3段、MS5段和MS11段非电毫秒延迟雷管起爆。试验时为排除钻孔及装药结构对振动频率的影响，所有炮孔钻爆参数保持一致：孔径40 mm、孔深1.8 m、堵塞0.2 m，炮孔间距0.5 m，崩落孔抵抗线0.5 m；采用2#岩石乳化炸药连续装药，药卷直径32 mm，单孔药量1.1 kg。在爆心距28 ～80 m范围内沿直线共布置4个振动测点。

图2　试验炮孔及振动测点布置图Fig.2 Arrangement of blastholes and vibration monitoring locations in the blast test

选择与自由面垂直的水平径向振动速度进行分析，实测振动时程曲线见图3。振动时程曲线明显地分为3段，第1段振动由掏槽孔爆破产生(只有一个自由面)，第2段和第3段由崩落孔爆破引起(具有两个自由面)。地表边坡属于开放尺度环境，而地下洞室属于受限空间，受介质空间结构条件的影响，地表边坡与地下洞室的爆破振动频率存在差异。李洪涛等[14]的研究结果表明，在孔深、孔径等参数基本相同的情况下，地表边坡爆破振动的主振频带更倾向于低频成分。所以，受到现场试验条件的限制，在垂直边坡上进行的全断面开挖爆破试验中所测得的振动(见图3)并不能完全反映地下洞室全断面开挖爆破振动的真实特性。但对比图3中掏槽孔爆破与崩落孔爆破产生的振动可以反映全断面开挖爆破产生的自由面对振动频率的影响。

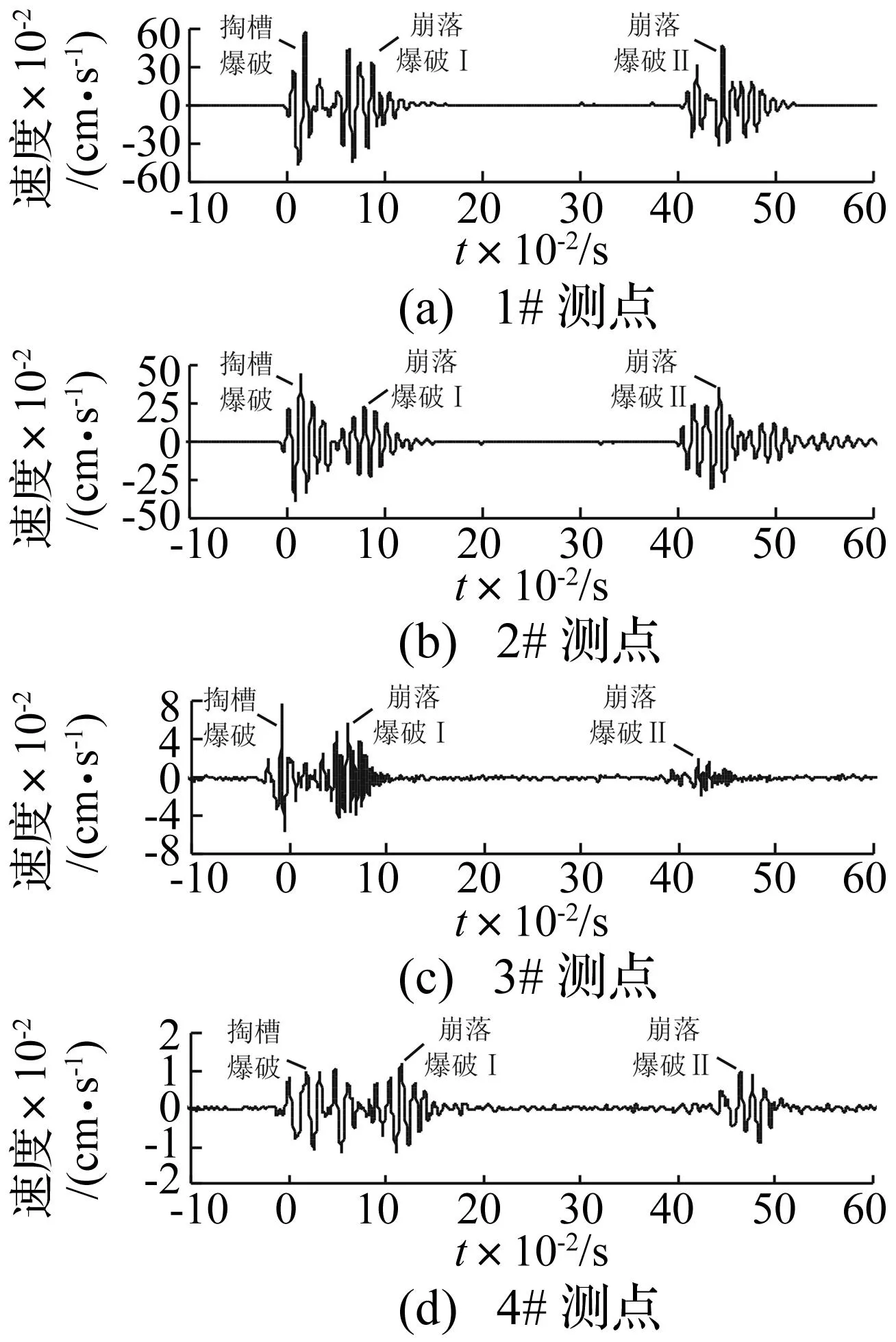
图3　实测水平径向振动时程曲线Fig.3 Recorded horizontally radial velocity-time histories in the blast test

1.2振动信号分析方法

传统的傅里叶变换可以获取信号较完整的频域信息。小波变换对低频信号具有较高的频率分辨率和较低的时间分辨率，对高频信号具有较高的时间分辨率和较低的频率分辨率，适合于爆破振动信号非平稳特性的分析。本文爆破振动信号分析采用傅里叶变换和小波包分析方法。

傅里叶变换的数学表达式如下：

(1)

式中：f(t)为振动随机信号；ω为圆频率；j为虚数单位；t为时间。F(ω)=|S(jω)|称为函数f(t)的幅值谱函数。

小波分析是把信号分解成低频和高频2部分，下一步将低频部分继续分解，而高频部分不再被分解。小波包分解是一种比小波变换更加精细的分析手段，在每层分解过程中同时对小波变换没有细分的高频部分作进一步的分解，从而提高了时频分辨率。爆破振动信号被分解到n层后，第i个频带上重构信号sn, i对应的能量设为En, i，则有：

(2)

式中：xi, k为重构信号sn, i各离散点对应的幅值(i=0，1，2,…，2n-1；k=1，2,…，N；N为离散信号的采样点数)。

爆破振动信号的总能量E0可以表示为：

(3)

爆破振动小波包分解到第n层时，各频带的振动能量占信号总能量的比例为：

pn,i=En,i/E0

(4)

由式(2)～式(4)可以得到爆破振动信号经小波包分解后各个频带的能量分布。采用的振动波形自记仪的采样频率为2 kHz, 根据Nyquist采样定理，该自记仪所采信号的最高频率为1 kHz，因此可对实测振动信号进行6层分解，对应的最低频带为0～15.625 Hz。Daubechies小波系列具有较好的紧支撑性、光滑性及近似对称性，目前被广泛应用于包括爆破振动信号在内的非平稳信号分析，其中最常用的是db8小波基[15-16]。本文也采用db8小波基进行振动信号小波包分析。

1.3分析结果

各段振动信号对应的幅值谱见图4，为了便于比较，这里将幅值谱的幅值进行归一化处理。以1#测点为例，可以看到，掏槽孔爆破振动对应的主频为71.9 Hz，两段崩落孔爆破产生的振动对应的主频分别为94.2 Hz和106.5 Hz，均高于掏槽孔爆破振动的主频。相比于掏槽孔爆破振动，所有测点的崩落孔爆破振动幅值谱曲线均向高频成分偏移，崩落孔爆破振动主频更高。

各段振动信号对应的小波包能量谱见图5。同样以1#测点为例，掏槽孔和崩落孔爆破振动信号的能量基本都在0.00～265.63Hz频带内。虽然3段振动信号的能量分布频带相同，但掏槽孔爆破振动信号在0～78.13 Hz频带内的能量占总能量的86%，在78.13～265.63 Hz频带内的能量仅占总能量的14%。而对于2段崩落孔爆破振动信号，高频(78.13～265.63 Hz)能量占总能量的比例分别为60%和76%。其他测点振动信号的小波包能量谱也可以得到同样的结论，即崩落孔爆破振动的高频能量比重明显高于掏槽孔爆破振动信号。

图4　掏槽孔和崩落孔爆破振动信号幅值谱比较Fig.4 Comparisons of amplitude spectrum curves for blasting vibration signals between cutting blastholes and breaking blastholes

图5　掏槽孔和崩落孔爆破振动信号小波包能量谱比较Fig.5 Comparisons of wavelet packet energy spectrum curves for vibration signals between cutting blastholes and breaking blastholes

尽管傅里叶变换和小波包分析这两种不同的数字信号处理方法得到的主振频带不完全相同，但从二者的分析结果可知：与掏槽孔爆破振动相比，崩落孔爆破振动的主频更大，高频振动部分占总能量的比例更高。试验中两类炮孔的钻孔及装药结构相同，振动测试条件一致，最大的差别在于掏槽孔爆破时只有掌子面一个自由面，而崩落孔爆破时除掌子面外，还有前一段炮孔爆破产生的自由面。这说明爆破产生的自由面影响了振动的频谱特性，致使振动频率变高。

2爆破振动数值模拟

前面只是从表象上展示了爆破产生的自由面对振动频率的影响，鉴于试验条件的限制，采用动力有限元分析软件LS-DYNA模拟试验中掏槽孔及崩落孔爆破产生的振动，在此基础上探讨爆破产生的自由面对振动频率的影响机理及其变化规律。

2.1几何模型

根据图2的爆破设计建立如图6的三维有限元模型，炮孔分布与尺寸与实际一致。模型尺寸为160 m×8 m×8 m(长×宽×高)，采用SOLID164单元进行网格划分，模型总共含有251 808个单元和271 830个节点。根据实际情况，模型的前表面设置为自由边界，其余五个面设置为透射边界以减小边界应力波反射的对计算结果的影响。在模拟崩落孔爆破时，首先将掏槽孔爆除的岩体单元从模型中删去，以体现掏槽孔爆破产生的自由面对后续崩落孔爆破振动的影响。

图6　有限元模型网格局部图Fig.6 Local view of the dynamic finite element model used for numerical simulation of blasting vibration

2.2材料模型及参数

LS-DYNA程序中提供的炸药材料可以直接模拟炸药的爆炸过程，采用JWL状态方程模拟炸药爆轰过程中压力和比容的关系，即：

(5)

式中：p为爆炸气体压力；V为相对体积；E0为单位体积初始比内能；A、B、R1、R2和w为与炸药相关的材料常数。计算中炸药密度取为1 300 kg/m3，爆速取为4 000 m/s，其他参数分别为A=214.4 GPa、B=0.182 GPa、R1=4.2、R2=0.9、w=0.15、E0=4.192 GPa[17]。

爆炸荷载作用下，炮孔近区岩体应变率效应明显，因此岩体材料采用包含应变率的塑性硬化模型，实际分析中通常考虑为Cowper-Symonds模型，它在屈服应力中引进应变率因子，表达式如下：

(6)

边坡表面岩体风化，其力学特性不同于内部岩体，计算中假定边坡坡面往里2.0 m范围内岩体参数按线性规律变化，2.0 m以外岩体参数不变，所采用的岩体力学参数见表1，表1中ρ和μ分别为岩体密度和泊松比。

表1　岩体力学参数

3自由面对振动频率的影响机理和变化规律

对于在均匀、各向同性、线弹性介质中起爆的球状药包，爆炸荷载激发振动的频域存在解析解，振动信号幅值谱的表达式为：

Fv(ω)=

(7)

式中：Fv(ω)为振动速度的幅值谱幅值；Sσ(jω)为爆炸荷载压力函数σ(t)的傅里叶变换；r为质点至球心的距离；cP为岩体纵波速度；λ、μ为拉梅系数；re为爆腔半径。

从式(7)可知，振动速度的频谱特性与爆心距(r)、岩体参数(cP、λ、μ)、钻孔爆破参数(re)及荷载的频谱特性有关。从理论上讲，对于图2所示的掏槽孔爆破和崩落孔爆破，在钻孔参数和装药结构相同的情况下，作用在炮孔壁上的荷载压力相同，那么同一爆心距处的振动频率应当是相同的。但是崩落孔爆破时存在前一段炮孔爆破产生的自由面，当爆炸压应力波传播至自由面时发生反射，产生回传的稀疏波，回传稀疏波与原应力波叠加，影响了远区的荷载压力。图7(a)给出了数值模拟的掏槽孔爆破和崩落孔爆破时10 m爆心距处的荷载压力时程曲线，从图7(a)可知，两条荷载曲线的形式类似，但崩落孔爆破时，由于自由面反射稀疏波的叠加作用，荷载的峰值降低，同时荷载上升时间和持续时间变短，导致荷载的能量向高频成分偏移，荷载频率变大，如图7(b)所示(为了便于比较，此处同样将幅值谱的幅值进行归一化处理)。从而进一步导致崩落孔爆破时振动的频率更高，高频部分占总能量的比例更高。

图7　10 m爆心距处爆炸荷载压力曲线及其幅值谱Fig.7 Blast loading pressures and their amplitude spectrum curves at the distance of 10 m from the blasting source

反射稀疏波的传播特征与岩体特性及传播距离有关，对于既定的岩体，当改变崩落孔与掏槽孔之间的排距，即改变崩落孔与自由面之间的距离时，崩落孔爆破时振动频率衰减变化见图8。由于傅里叶主频在传播过程中会出现局部突变现象，不能很好地反映振动的频谱构成及其衰减规律，因而此处采用质心频率(平均频率)[18]，其表达式为：

(8)

式中：fc为质心频率，Fi为频率fi对应的振动速度幅值谱的幅值。

由图8可知，爆源距自由面越远，振动频率越低，反之则振动频率越高。这种现象在理论上也容易解释，当增大爆源与自由面之间的距离时，向自由面传播的压缩波及反射稀疏波的传播路径变长，应力波在传播过程中不断衰减，特别是在爆源近区衰减速率较快，因而反射稀疏波的应力大小随传播距离的增加而减小，对原应力波的干扰也随之减小，根据前文的分析，因而振动频率较低。建(构)筑物的自振频率一般较低，低频振动对建(构)筑物更为不利。因此，从振动频率角度来看，减小爆源与自由面之间的距离、增大爆破振动频率可以降低爆破振动对建(构)筑物的危害。

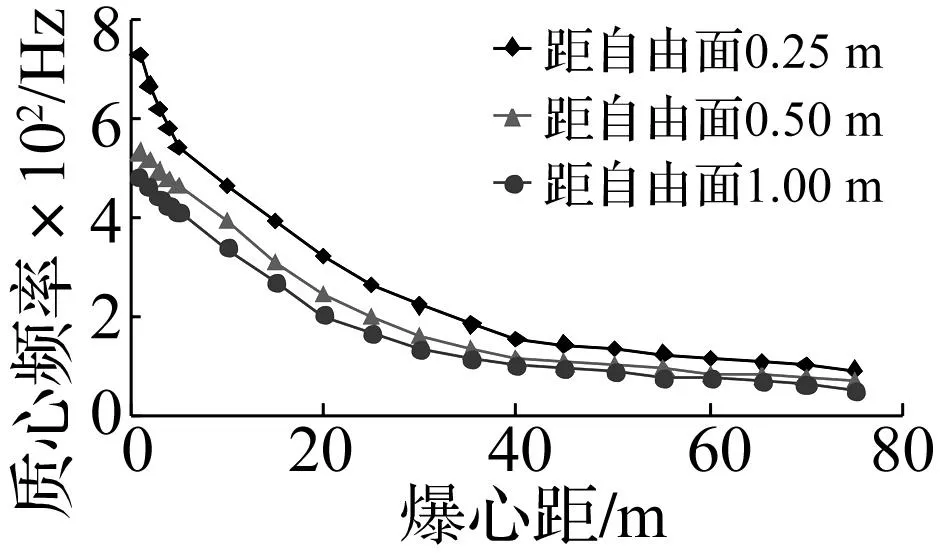
图8　距自由面不同距离时振动频率衰减比较Fig.8 Comparison of vibration frequency attenuations at different distances from the blasting source to the free surface

4结论

通过现场试验数据分析和数值模拟，研究了全断面毫秒延迟爆破过程中爆破产生的自由面对振动频率的影响机理和变化规律，得到了如下结论：

(1) 掏槽孔爆破为后续的崩落孔爆破创造了新的自由面，在该自由面反射的稀疏波与原应力波叠加致使远区荷载压力上升时间和持续时间变短，引起荷载的频率变大，从而导致其振动频率变高、高频振动能量占总能量的比重增加。现场试验监测结果验证了数值模拟分析结论的可靠性。

(2) 爆源与自由面之间的距离越小，爆破振动频率越高，反之则振动频率越低，从振动频率的角度来看，较好的自由面条件可以减小爆破振动对建(构)筑物的危害。

(3) 地下洞室全断面爆破开挖，掏槽孔在只有一个自由面的条件下爆破，其质点峰值振动速度大，振动频率低，而建(构)筑物的自振频率一般较低，因此与其他类型炮孔相比，掏槽孔爆破产生振动对建(构)筑物的危害更大。

影响爆破振动频率的因素众多，本文只是初步研究了全断面爆破过程中爆破产生的自由面对振动频率的影响，钻孔参数、装药结构、多孔爆破相互作用以及雷管延时间隔和误差等因素的影响，还需要做进大量的研究。

参 考 文 献

[ 1 ] Henrych J, Major R. The dynamics of explosion and its use [M]. Amsterdam, Elsevier, 1979.

[ 2 ] Heilig J, Zoitsas A, Cox N. Free face blasting: is it the best for quarry[C]//In: Proceedings of the 41st Annual Conference Institute of Quarrying, Australia, 1997: 23-29.

[ 3 ] Singh P K. Blast vibration damage to underground coal mines from adjacent open-pit blasting[J].International Journal of Rock Mechanics and Mining Sciences, 2002, 39(8): 959-973.

[ 4 ] Nateghi R. Prediction of ground vibration level induced by blasting at different rock units[J].International Journal of Rock Mechanics and Mining Sciences, 2011, 48(6): 899-908.

[ 5 ] 陈星明，肖正学，蒲传金. 自由面对爆破地震强度影响的试验研究[J]. 爆破，2009，26(4)：38-40.

CHEN Xing-ming, XIAO Zheng-xue, PU Chuan-jin. Experimental study on influence blasting earthquake strength to free faces[J].Blasting, 2009, 26(4): 38-40.

[ 6 ] 梁雪松. 自由面对爆破振动的影响研究[D]. 沈阳：东北大学，2013.

[ 7 ] 池恩安，赵明生，梁开水，等. 自由面数量对爆破地震波时频特性影响分析[J]. 爆破，2013，30(2)：16-20.

CHI En-an, ZHAO Ming-sheng, LIANG Kai-shui, et al. Influence of number of free surface on time-frequency characteristics of blasting seismic wave[J].Blasting, 2013, 30(2): 16-20.

[ 8 ] 许海亮，张继春，杨红，等. 钻孔爆破振动速度计算公式及其简化的探讨[J].同济大学学报:自然科学版，2007，35(7)：899-903.

XU Hai-liang, ZHANG Ji-chun, YANG Hong, et al. Investigation on calculating formula of vibration velocity in drilling blasting and its simplification[J].Journal of Tongji University:Natural Science, 2007, 35(7): 899-903.

[ 9 ] Wu C Q, Hao H. Numerical study of characteristics of underground blast induced surface ground motion and their effect on above-ground structures. Part I. Ground motion characteristics[J].Soil Dynamics and Earthquake Engineering, 2005, 25(1): 27-38.

[10] 邓华锋，张国栋，王乐华，等. 导流隧洞开挖施工的爆破振动监测与分析[J]. 岩土力学，2011，32(3)：855-860.

DENG Hua-feng, ZHANG Guo-dong, WANG Le-hua, et al. Monitoring and analysis of blasting vibration in diversion tunnel excavation[J].Rock and Soil Mechanics, 2011, 32(3): 855-860.

[11] Blair D P, Armstrong L W. The influence of burden on blast vibration[J].Fragblast, 2001, 5(1/2): 108-129.

[12] Brent G F, Smith G E, Lye G N. Studies on the effect of burden on blast damage and the implementation of new blasting practices to improve productivity at KCGMs fimiston mine[J].Fragblast, 2002, 6(2): 189-206.

[13] Uysal Ö, Arpaz E, Berber M. Studies on the effect of burden width on blast-induced vibration in open-pit mines[J].Environmental Geology, 2007, 53(3): 643-650.

[14] 李洪涛，杨兴国，舒大强，等. 不同爆源形式的爆破地震能量分布特征[J]. 四川大学学报:工程科学版，2010，42(1)：30-34.

LI Hong-tao, YANG Xing-guo, SHU Da-qiang, et al. Study on energy distribution characteristics of seismic waves induced by different forms of blasting resource[J]. Journal of Sichuan University:Engineering Science Edition, 2010, 42(1): 30-34.

[15] 凌同华，李夕兵. 单段爆破振动信号频带能量分布特征的小波包分析[J]. 振动与冲击，2007，26(5)：41-43.

LING Tong-hua, LI Xi-bing. Features of energy distribution of single deck blast vibration signals with wavelet packet analysis[J].Journal of Vibration and Shock, 2007, 26(5): 41-43.

[16] 李兴华，龙源，纪冲，等. 基于小波包变换的高程差对爆破震动信号影响分析[J]. 振动与冲击，2013，32(4)：44-47.

LI Xing-hua, LONG Yuan, JI Chong, et al. Influence of height difference based on wavelet packets transformation on blasting vibration signals[J].Journal of Vibration and Shock, 2013, 32(4): 44-47.

[17] Li Hai-bo, Xia Xiang, Li Jian-chun, et al. Rock damage control in bedrock blasting excavation for a nuclear power plant[J].International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 210-218.

[18] 卢文波，张乐，周俊汝，等. 爆破振动频率衰减机制和衰减规律的理论分析[J]. 爆破，2013，30(2)：1-6.

LU Wen-bo, ZHANG Le, ZHOU Jun-ru, et al. Theoretical analysis on decay mechanism and law of blasting vibration frequency[J].Blasting, 2013, 30(2): 1-6.

Influences of blast-created free surfaces on blasting vibration frequencies during full-face excavation

YANGJian-hua1,LUWen-bo2,YANPeng2,JIANGQing-hui1,ZHOUChuang-bing1(1. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China；2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

Abstract:With methods of spectral analysis of vibration signals and numerical simulation of blasting vibration, the influences of blast-created free surfaces on blasting vibration frequencies during underground full-face excavation were investigated here. The vibration signals were measured from a specially designed small-scale blast test, where blastholes were detonated under different free surface conditions. The results showed that the presence of free surfaces results in higher blasting vibration frequencies and an increasing proportion of vibration energy with higher frequencies to total energy; the smaller the distance between blasting sources and free surfaces, the higher the blasting vibration frequencies; this is since the rarefaction waves reflected on free surfaces are superimposed onto the blast-induced initial compressive stress waves, and this causes the rising time and duration of the far-field blast loading pressure becomes shorter to lead to an increase in frequencies of loading; from the view-point of vibration frequency, the damage of structures due to blasting vibration can be mitigated with a better free surface condition. The reliability of the results was demonstrated with the vibration monitoring in the blast test.

Key words:underground opening; blasting; free surface; vibration frequency

中图分类号:TD235.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.029

通信作者姜清辉 男，博士，教授，1972年生

收稿日期：2014-08-19修改稿收到日期：2014-12-05

基金项目：国家自然科学基金资助项目(51509126;51279135)

第一作者 杨建华 男，博士，讲师，1986年生