函数与方程思想

●杨　威　莫芬利　(镇海中学　浙江宁波　315200)



函数与方程思想

●杨威莫芬利(镇海中学浙江宁波315200)

1　知识内容

函数与方程是2个不同的概念，但它们之间有着密切的联系:方程f(x)=0的解就是函数y= f(x)的图像与x轴交点的横坐标，函数y=f(x)也可以看作二元方程f(x)－y=0通过方程进行研究．函数与方程的思想是中学数学的基本思想之一．

函数思想，是用运动和变化的观点、集合与对应的思想，去分析和研究数学问题中的数量关系，构造函数或建立函数关系，利用函数的图像和性质去分析问题和解决问题．方程思想，就是通过分析问题中变量间的等量关系，设定未知数然后建立方程或方程组，通过解方程或方程组使问题获得解决．方程的思想是对方程概念的本质认识，用于指导解题就是善于利用方程或方程组的观点观察和处理问题．方程思想是动中求静，研究运动中的等量关系．

2　命题分析

函数是高中数学的一条主线，因此函数与方程的思想方法，渗透到中学数学的各个领域，在解题中有着广泛的应用，也是历年高考的重点．函数思想在解题中的应用主要表现在2个方面:一是借助有关初等函数的性质，解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题;二是在问题的研究中，通过建立函数关系式或构造中间函数，把所研究的问题转化为讨论函数的有关性质，达到化难为易、化繁为简的目的．许多有关方程的问题可以用函数的方法解决，反之，许多函数问题也可以用方程的方法来解决．具体体现在:函数与方程、不等式之间可以相互转化;数列也是一种特殊的函数，用函数的观点处理数列问题是一种非常重要的方法;在立体几何和解析几何中，也经常运用联立方程或者建立函数表达式的方法加以解决．

3　典题剖析

分析由f(x)的解析式易得

于是y=f(x)－g(x)=f(x)+f(2－x)－b，

因此，y=f(x)－g(x)恰有4个零点等价于方程f(x)+ f(2－x)－b=0有4个不同的解，即函数y=b与函数y= f(x)+f(2－x)的图像有4个公共点．如图1，由图像可知

图1

点评此题考查了函数的零点个数问题，在充分地利用了“函数的零点”与“方程的根”的密切关系后，通过数形结合转化为常值函数与分段函数有4个交点时的求参数范围问题．

例2函数f(x)=ax2+bx+c(其中a≠0)的图像关于直线对称．据此可推测，对任意的非零实数a，b，c，m，n，p，关于x的方程m［f(x)］2+nf(x)+p=0的解集都不可能是()

A．{1，2}B．{1，4}

C．{1，2，3，4}D．{1，4，16，64}

分析从二次函数对称性的角度来看，在方程m［f(x)］2+nf(x)+p=0中，可将f(x)看成未知数，根据m，n，p取值不同，f(x)可得出1个、2个解或无解．当f(x)有1个解时，即f(x)=k，代入f(x)的解析式，由a，b，c取值不同，此方程f(x)=k也可能有1个、2个解或者没有解．由函数f(x)= ax2+bx+c(其中a≠0)的图像关于直线对称可知，当f(x)=k有2个解时，这2个解x1，x2关于对称，而a，b取值不定，故2个解可取任意值，因此选项A，B可能．当f(x)有2个解时，对应的x可能有4个解，f(x)=u的解x1，x2和 f(x)=v的2个解x3，x4分别应关于对称．在选项C中，1，4，2，3均关于x=2．5对称，因此可能正确．而选项D中的4个数不能满足上述条件，因此不可能是方程的解．故选D．

另外，从“小题小做”的角度来说，本例可以采用特例法简洁快速地解决．对方程m［f(x)］2+ nf(x)+p=0中m，n，p分别赋值求出f(x)，再代入f(x)=0求出并检验即可．

点评本题充分利用了一元二次方程和二次函数的关系，将方程的解转化为函数f(x)的值，再一次转化为方程f(x)=k的解，而利用二次函数y=f(x)的图像得出所有的解必须是关于某一条直线对称，使问题得解．

例3定义:如果函数y=f(x)在定义域内给定区间［a，b］上存在x0(其中a＜x0＜b)，满足，则称函数y=f(x)是区间［a， b］上的“平均值函数”．若函数f(x)=－x2+mx是区间［－1，1］上的平均值函数，求实数m的取值范围．

分析根据定义，存在x0∈(－1，1)使得，化简得

解法1(分离参变量法)

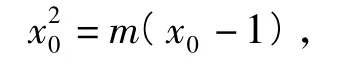
因为x0∈(－1，1)，令t=x0－1∈(－2，0)，所以

解法2(图像法)

1)构造1个函数．

利用二次方程根的分布:因为根的个数不确定，因此需要进行分类讨论．

若在(－1，1)上只有1个根，则只需g(－1)g(1)＜0或

综上可知，实数m的取值范围是(－∞，0］．

2)构造2个函数(等价转化为2个函数图像有交点)．

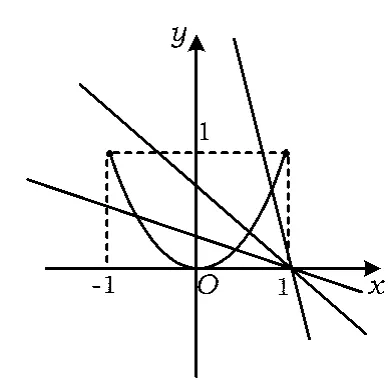
图2

点评本题等价转化为一元二次方程的有解问题:解法1适用于能方便分离出参变量的一般的方程有解问题，通过求已知变量范围的函数的值域来解决问题;解法2中的2种构造函数的方法，其核心思想都是数形结合，即通过转化为研究1个函数图像与x轴的交点个数，或2个函数图像间的交点个数来解决．

分析根据直线与椭圆相交，联立方程

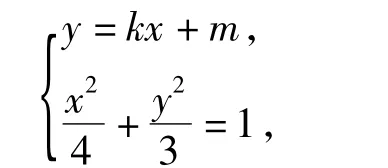
化简整理得

设点A，B，P的坐标分别为(x1，y1)，(x2，y2)，(x0，y0)，则

因为点P在椭圆C上，所以

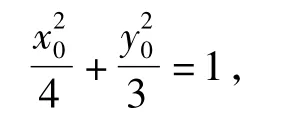
经检验满足Δ＞0．又

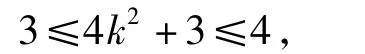
点评求圆锥曲线有关的最值和范围问题时，往往需要选择一个适当的参数作为自变量来表示所研究的对象，也即构建一个函数，再通过研究函数的值域来解决问题．而这一过程中最关键的是寻找参数的变化范围(特别是判别式Δ)和掌握求函数值域的各种方法．

例5已知数列{an}为等差数列，且a1，a3，a8+1成等比数列，2a1，a2+a3，a8成等差数列．

1)求数列{an}的通项公式;

分析1)采用基本量法把条件和结论统一化归为首项和公差的关系式．设数列{an}的公差为d，由

得a1=d=1，故an=n．

2)该问题是数列中的恒成立问题，本质上是先求不等式左边关于n的最小值，再解关于m的不等式．

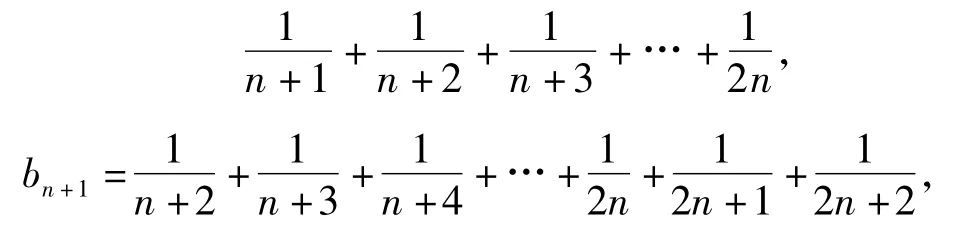
则

从而数列{bn}是单调递增数列．因此当n≥2时，bn的最小值为

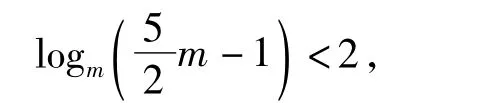
点评数列是特殊的函数，因此在碰到数列中的不等式恒成立问题时可以构造函数后采取函数中恒成立问题的一般方法加以解决．

4　精题集萃

A．－2B．－4C．－8D．不能确定

2．在公差为d、各项均为正整数的等差数列{an}中，若a1=1，an=81，则n+d的最小值为()

4．已知实数a，b满足a3－b3=4，a2+ab+ b2+a－b=4，则a－b =______．

6．已知f(x)是定义在R上的偶函数，对任意的x∈R，都有f(2+x)=－f(x)，且当x∈［0，1］时，f(x)=－x2+1，则方程f(x)=k，k∈［0，1)在［－1，5］的所有实根之和为______．

7．设二次函数f(x)=ax2－4x+c(其中a≠0)的值域为［0，+∞)，且f(1)≤4，求的最大值．

1)求椭圆C的方程;

参考答案

1．B2．D3．A

7．解由二次函数y=ax2－4x+c的值域为［0，+∞)，知a＞0，且，即a＞0，c＞0，且ac=4，从而

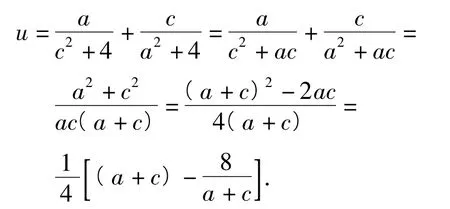
令x=a+c，由f(1)≤4，得a+c≤8，又a＞0，c＞0，且ac=4，得

设N(x，y)，则

2)设A(x1，y1)，B(x2，y2)，P(x，y)，直线AB的方程为y=k(x－3)．由整理得

由Δ=(24k2)2－16(9k2－1)(1+4k2)＞0，得

由点P在椭圆上，得

将x1+x2，x1x2代入上式得

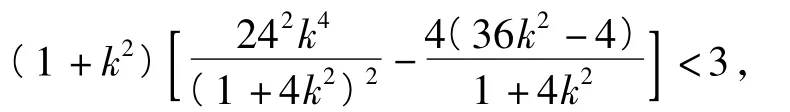
由式(1)，得

联立式(2)，得3＜t2＜4，因此