三角函数与平面向量的复习
2016-05-19苗孟义三山高级中学浙江慈溪315300黄国员慈溪市教育局教研室浙江慈溪315300
●苗孟义 (三山高级中学 浙江慈溪 315300) ●黄国员 (慈溪市教育局教研室 浙江慈溪 315300)
三角函数与平面向量的复习
●苗孟义(三山高级中学浙江慈溪315300)●黄国员(慈溪市教育局教研室浙江慈溪315300)
1 命题分析
回顾近几年浙江省数学高考试题中关于“三角函数与平面向量”的考题,给我们一种“题在书外、根在书中”的感觉(以2015年为例):文、理科第11题,与《数学(必修4)》第147页复习参考题类似;文科第13题呈现熟悉,理科第15题呈现新颖,理科第16题更关注通性通法,考查有价值的常规方法的应用,凸显学生运用数学思想方法,把数学的知识与技能转化为分析问题和解决问题的能力.全卷一般有3~4个三角函数与平面向量的试题,分值占15%~20%.
三角函数主要考查:三角函数名称、角、关系式的变换;三角函数图像与性质,图像的变换,三角函数的单调性、奇偶性、周期性、对称性、最值等;简单的三角恒等变换,包括两角和与差的正弦、余弦和正切公式、二倍角公式等,合理运用三角公式是解决三角函数的图像与性质、三角恒等变换等问题的关键.
解三角形主要考查:内角和定理与正弦(余弦)定理,解三角形的边、角、面积及判断三角形形状等.
平面向量主要考查:平面向量的几何意义、基向量转化、坐标法.
在高考试题中,三角函数试题的考查难度不大,容易得满分;平面向量试题往往短小精悍,内涵丰富,有挑战性.2015年浙江省数学高考理科试题对有关向量问题的考查,悄悄地由平面转向空间,值得关注.
2 典题剖析
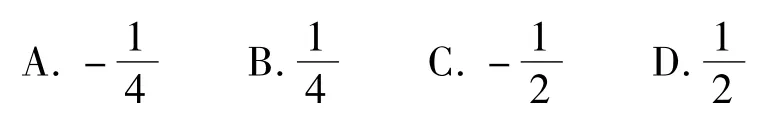
3)设△ABC的内角A,B,C所对的边a,b,c成等比数列,则的取值范围是()

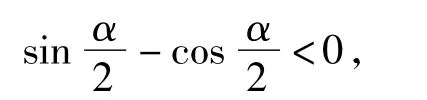

故选A.
3)

因为b2=ac,即,由

评析此题组考查同角三角函数关系、两角和与差的正弦(正切)公式.其解答过程集中体现在运算上,是突出对运算能力考查的一组试题,关键是对公式的选择和运算方向的把握.在选择公式、确定运算路径时,应本着从简的原则,尽量缩短运算路径,简化运算过程,提高运算的准确率,这些都是对运算能力的考查要求.
2)已知函数f(x)=Asin(ωx+φ)(其中A,ω,φ均为正常数)的最小正周期为π,当时,函数f(x)取得最小值,则下列结论正确的是()
A.f(2)<f(-2)<f(0)
B.f(0)<f(2)<f(-2)
C.f(-2)<f(0)<f(2)
D.f(2)<f(0)<f(-2)
3)函数f(x)=cos(ωx+ φ)的部分图像如图1所示,则f(x)的单调递减区间为()

图1
分析1)向右平移φ个单位后,得到
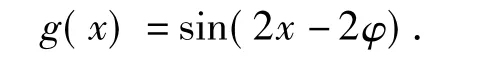
因为|f(x1)-g(x2)|=2,所以当|x1-x2|取最小值时,刚好是取2个函数相邻的最大值与最小值点.令,则
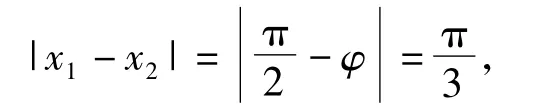
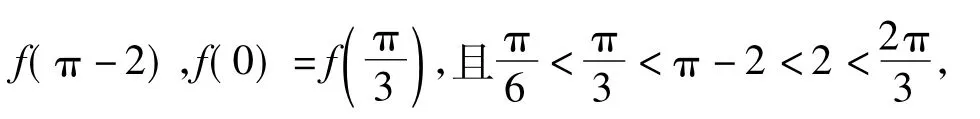
从而

故选A.
3)由五点作图法知



评析三角函数作为重要的基本初等函数,是高考必考的内容之一.对函数图像与性质(如:定义域、值域、周期性、对称性、奇偶性、单调性、最值等)的掌握情况可以在三角函数中得到体现.公式运用及其变形能力、运算能力等可以在这些问题中进行考查,在复习时要注意基础知识的理解与落实.
例31)已知平面向量a,b,且|b|=2,b· (2a-b)=0,则|tb+(1-2t)a|(其中t∈R)的最小值为_____.
3)若平面向量a,b,e满足|e|=1,a·e=1, b·e=2,|a-b|=2,则a·b 的最小值为_____.
分析1)方法1由|b|=2,b·(2a-b)=0知a·b=2,从而a在b方向上的投影为不妨设b=(2,0),a=(1,y),y任意,因为
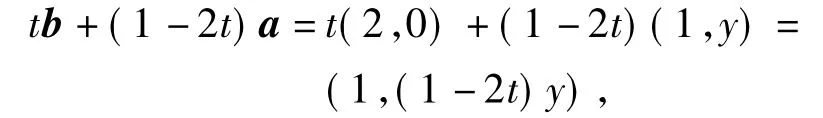
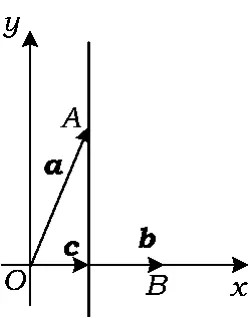
图2
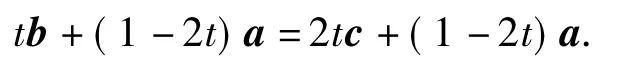
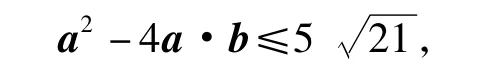
3)因为(a+b)·e=3≤|a+b|·|e|,所以
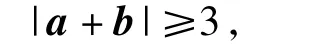
从而
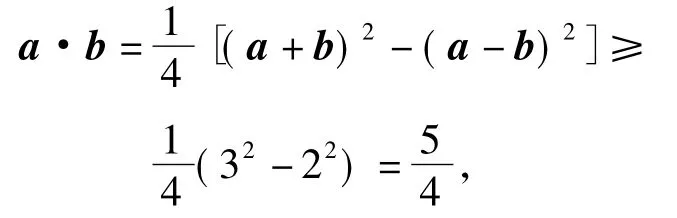
评析平面向量与不等式结合的问题,解题的关键是利用向量知识将问题转化为不等式问题,通过解不等式、数形结合、极化恒等式来求最值或范围.向量与不等式的结合,既考查了学生的创新数学素养,又加强了对“双基”的考查,特别是向量的坐标表示及运算.这种命题形式符合考纲要求,从学科的整体高度和思维价值的高度考虑问题,在知识网络的交汇处设计试题,对数学基础知识的考查达到必要的深度.
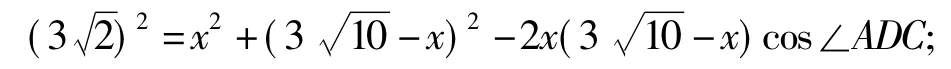
在△ABD中,
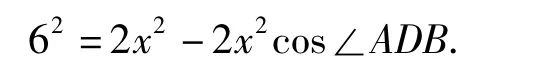
方法2如图3,过点C作边AB所在直线的垂线,垂足为E,过点D作DF⊥AB,垂足为F.由得 AE=CE=3,则
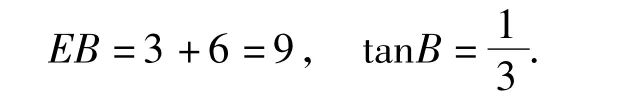

图3
又AD=BD,在Rt△DFB中,
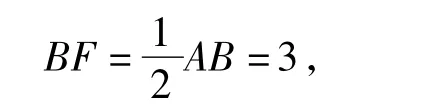
评析方程思想是通过列方程,找到相关量的关系,通过方程关系的转化得到需要的量进而解决问题.列方程可以将逆向思维的算术问题转化为正向思维的代数问题,学生如果能牢固树立这一思想意识,可以减少很多不必要的思考.另外通过数形结合的思想,借助图形,甚至建立坐标系等,都可以比较快捷地解决此类问题.
1)求函数f(x)的单调递增区间;
2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,若,△ABC的面积为,求的取值范围.
分析1)先利用诱导公式、二倍角公式、三角恒等变换化简解析式



因为△ABC为锐角三角形,所以
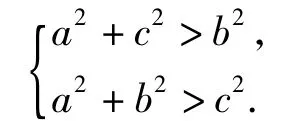
由a2=b2+c2-1,知

评析正确化简函数关系式是解题的关键,要警惕“一开始算错,接下来白做!”审题时要注意△ABC是锐角三角形.
3 精题集萃
A.2B.4C.6D.8
A.[-1,11]B.[1,13]
1)求ω的值;
参考答案




