立体几何复习要点例析

●沈顺良　(海盐县教育研究与教师培训中心　浙江海盐　314300)



立体几何复习要点例析

●沈顺良(海盐县教育研究与教师培训中心浙江海盐314300)

1　知识内容

立体几何的主要内容分以下几类:一是几何体的三视图和直观图、几何体体积和表面积;二是空间点、线、面的位置关系，空间线线、线面、面面平行与垂直的判定与性质及其运用;三是空间2条直线所成角、直线与平面所成角和二面角的概念和求解;四是空间向量及其运算，运用空间向量方法解决空间立体几何中的一些简单问题．

2　命题分析

纵观近几年的浙江省数学高考试卷，从目标要求看，立体几何重点考查学生的空间想象能力、逻辑推理能力，也渗透着对等价转化思想和数形结合思想运用的要求;从具体知识点的考查看，选择题和填空题的考查常以空间点、线、面的基本关系(主要是平行与垂直)的判断、常见空间图形基本性质的认识(含三视图的识别)以及面积、体积计算为主，解答题以常见图形(如三棱柱、四棱柱、三棱锥、四棱锥等)或其组合形式为载体，第1)小题一般考查平行与垂直的相关证明，第2)小题一般考查空间角的问题，综合法和向量法的运用在其中各有特色，还可能涉及存在性、动点和最值等不同的探究转化要求，值得关注．

3　典题剖析

考点1轨迹与几何体问题

例1如图1，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是()

图1

A．直线B．抛物线

C．椭圆D．双曲线的一支

(2015年浙江省数学高考文科试题第7题)

分析由动点P满足∠PAB=30°得到动点P的轨迹是以平面α的斜线AB为旋转轴、以A为顶点、轴截面顶角为60°的圆锥侧面，再根据动点P在平面α上，得到点P的轨迹是圆锥与平面α的公共点，即为椭圆．故选C．

评注本题中满足一定条件的动点形成了基本几何体圆锥的侧面，既考查了几何条件下动点的轨迹，又考查了基本几何体．

考点2三视图问题

例2一个正方体被一个平面截去一部分后，剩余部分的三视图如图2所示，则截去部分体积与剩余部分体积的比值为()

(2015年全国数学高考新课标卷理科试题第6题)

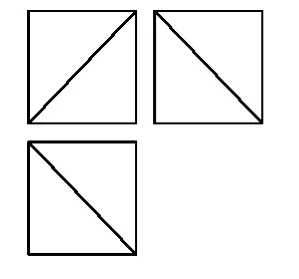
图2

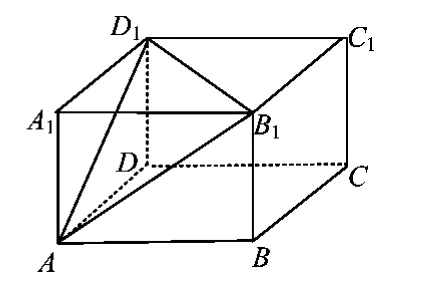
图3

分析本题是给定正方体背景下的三视图问题，主要考查三视图与直观图转化中的空间想象、体积的计算．由于三视图都是正方形且添上了对角线，因此截正方体后的直观图为如图3所示正方体ABCD-A1B1C1D1中截去四面体A-A1B1D1．设正方体棱长为a，则

故剩余几何体体积为

考点3角与距离问题

例3如图4所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过点A1，D，E的平面交CD1于点F．

图4

1)证明:EF∥B1C．

2)求二面角E-A1D-B1的余弦值．

(2015年安徽省数学高考理科试题第19题)

分析1(综合法)由3个正方形条件，将原多面体补形为正方体(如图5)．

1)过点A1，D，E的平面即为平面A1DC1，故F 为CD1的中点，于是EF∥B1C．

2)所求二面角即为平面A1DC1与对角面A1B1CD所成锐角，只要取B1C的中点O和A1D的中点G，联结C1O，C1G，OG，因为△C1A1D，△C1B1C都是等腰三角形，所以C1O⊥B1C，C1G⊥A1D，又OG⊥A1D，故∠C1GO为二面角E-A1D-B1的平面角．而C1O⊥A1B1，得C1O⊥平面A1B1CD，令正方体棱长为a，则，从而所求余弦值为

图5

分析2(向量坐标法)由条件中的3个正方形知过点A的3条棱两两垂直，解决第2)小题可建立如图6所示的空间直角坐标系，得A(0，0，0)，B(1，0，0)，D(0，1，0)，A1(0，0，1)，B1(1，0，1)，D1(0，1，1)，E(0．5，0．5，1)，通过待定系数法求出面A1DE和面A1B1CD的法向量分别为n1=(－1，1，1)和n2=(0，1，－1)，从而二面角E-A1D-B1的余弦值为

图6

评注分析1中将原多面体补形为正方体，对空间点线面的关系有较好的直观辅助作用，在立体几何综合法解决中有广泛的运用．本题的已知条件也为直接正交建系提供了方便．

考点4几何量的最值问题

例4如图7，AB是⊙O的直径，点C是⊙O上异于A，B的点，PO垂直于⊙O所在的平面，且PO=OB=1．

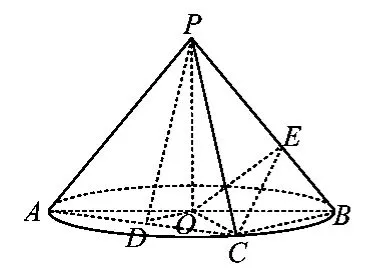
图7

1)若D为线段AC的中点，求证AC⊥平面PDO;

2)求三棱锥P-ABC体积的最大值;

(2015年福建省数学高考文科试题第20题)

分析11)要证明AC⊥平面PDO，只需证明AC垂直于面PDO内的2条相交直线．首先由PO垂直于⊙O所在的平面，可证明PO⊥AC．又OA= OC，D为AC的中点，从而AC⊥OD，进而证明结论．

2)三棱锥P-ABC中，高PO=1，要使得三棱锥P-ABC体积最大，则△ABC面积最大，又AB=2是定值，故当AB边上的高最大时△ABC的面积最大，此时高为半径，进而求得

3)要求线段长之和的最小值，应将2条线段化归到同一平面内．将平面BCP绕PB旋转至平面BC'P，使之与平面ABP共面(如图8)，此时线段OC'的长度即为CE+OE的最小值．又PB=BC'=，故当O，E，C'共线时，CE+OE取得最小值．由条件E为PB的中点，得

图8

分析2第3)小题还可以用以下2种方法:

①解△OC'P求OC'长度．由余弦定理得

考点5平面图形的折叠问题

1)证明:CD⊥平面A1OC;

2)若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角的余弦值．

(2015年陕西省数学高考理科试题第18题)

分析11)在图9中由条件可得:BE⊥AO，OC⊥CD，BE∥CD，这些条件在图10中也成立，故CD⊥AO，得到CD⊥平面A1OC．

葛根是苏伯维尔的君药，而葛根素则是葛根的有效成分，研究表明其具有解热〔4〕，镇痛〔5〕，抗菌、抗感染〔6〕，降血压〔7〕，降血糖、血脂〔8〕，抗氧化，抗肿瘤，解酒〔9〕等作用，与苏伯维尔的功能主治一致，所以本实验选择葛根素作为苏伯维尔水提工艺的含量测定指标。为考察提取情况，首先对葛根素含量进行考察，其次对浸膏得率进行考察，试验分析得出：葛根素含量比浸膏得率更好地反映药材的提取情况，故设计葛根素含量与浸膏得率的权重系数为8：2。为确保水提工艺的合理性，本实验进行了验证试验，结果表明，正交试验优选出的水提工艺合理可行。

图9

图10

2)显然二面角B-A1C-D是钝角，可以将此二面角分解为二面角B-A1C-O，O-A1C-D之和．由第1)小题知二面角O-A1C-D为直角，如图11，作BP⊥A1C，联结OP，由BO⊥平面AOC可证∠OPB是二面角B-A1C-O的平面角，，根据诱导公式二面角B-A1C-D的余弦值即为，故平面A1BC与平面A1CD夹角的余弦值为

分析2(向量坐标法)解决第2)小题还可以运用空间向量法．由平面A1BE⊥平面BCDE，而BE⊥OA1，BE⊥OC，知∠A1OC为二面角A1-BE-C的平面角，从而

图11

如图12，以O为原点，建立空间直角坐标系，则

图12

得

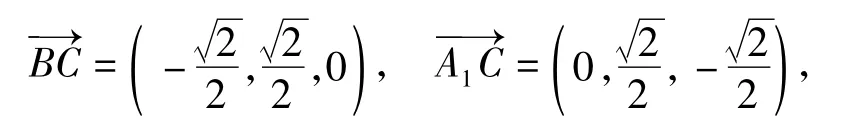
用待定系数法可求得平面A1BC的法向量n1=(1，1，1)，平面A1CD的法向量n2=(0，1，1)，从而

即平面A1BC与平面A1CD夹角的余弦值为

考点6动点成线、动线成面问题

图13

1)求平面PAB与平面PCD所成二面角的余弦值;

2)点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线段BQ的长．

(2015年江苏省数学高考试题第22题)

分析1(补形)将原图补为如图14所示棱长为2的正方体．

图14

1)所求为二面角D-PO-A，联结OA，OD，易证∠DOA为所求二面角的平面角．由

得

2)点Q是线段BP上的动点，动直线CQ在平面CPB上，直线DP与CQ所成角最小时，即为直线DP与平面CPQ所成角．如图15作OR⊥PB，垂足为R，则∠OPR即为直线CQ与DP所成角的最小角．由

图15

分析2(坐标法)本题的另一解法是坐标系下的空间向量法，以为正交基建立空间直角坐标系，则B(1，0，0)，C(1，1，0)，D(0，2，0)，P(0，0，2)．

1)分别求出2个平面的法向量为(0，2，0)，(1，1，1)，即可求2个平面所成二面角的余弦值．

令1+2λ=t，其中t∈［1，3］，则

4　精题集萃

1．若直线l1和l2是异面直线，l2在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是()

A．l至少与l1，l2中的1条相交

B．l与l1，l2都相交

C．l至多与l1，l2中的1条相交

D．l与l1，l2都不相交

2．若空间中n个不同的点两两距离都相等，则正整数n的取值()

A．大于5B．等于5

C．至多等于4D．至多等于3

3．在三棱柱ABC-A1B1C1中，∠BAC=90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形．设点M，N，P分别是AB，BC，B1C1的中点，则三棱锥P-A1MN的体积是_____.

4．在直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM 与AN 所成角的余弦值为_____．

5．正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为______．

6．如图16，在正方体ABCD-A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是______．

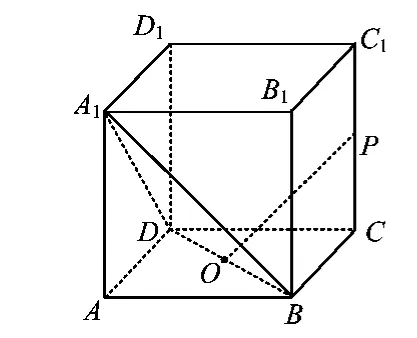
图16

图17

7．如图17，△PDC所在的平面与长方形ABCD所在的平面垂直，PD=PC=4，AB=6，BC=3．点E 是CD边的中点，点F，G分别在线段AB，BC上，且AF=2FB，CG=2GB．

1)证明:PE⊥FG;

2)求二面角P-AD-C的正切值;

3)求直线PA与直线FG所成角的余弦值．

8．如图18，在长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1和D1C1上，A1E= D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形．

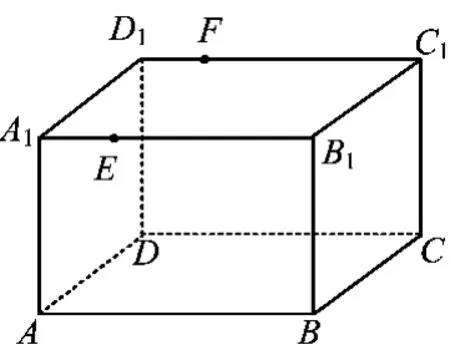
图18

1)在图18中画出这个正方形(不必说明画法和理由);

2)求直线AF与平面α所成角的正弦值．

参考答案

1．A2．C

7．1)证明因为PD=PC且点E为CD的中点，所以PE⊥DC．又平面PDC⊥平面ABCD，且平面PDC∩平面ABCD=CD，PE⊂平面PDC，从而PE⊥平面ABCD．又FG⊂平面PDC，故PE⊥FG．

2)解由ABCD是矩形，得AD⊥DC，又平面PDC⊥平面ABCD，且平面PDC∩平面ABCD=CD，AD⊂平面ABCD，得

又CD⊂平面PDC，PD⊂平面PDC，于是

从而∠PDC即为二面角P-AD-C的平面角．在Rt△PDE中，，得

3)解由AF=2FB，CG=2GB，得

于是∠PAC为直线PA与直线FG所成角或其补角．在△PAC中，

由余弦定理可得

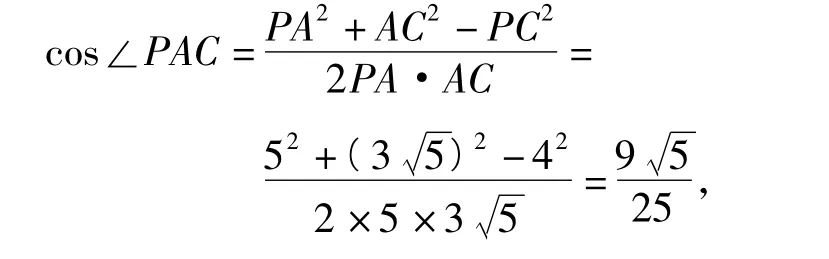
8．解1)交线围成的正方形EHGF如图19所示．

图19

2)作EM⊥AB，垂足为M，则AM=A1E=4，EM= AA1=8．因为四边形EHGF为正方形，所以