自选模块备考策略

●范东晖　(北仑中学　浙江宁波　315800)



自选模块备考策略

●范东晖(北仑中学浙江宁波315800)

2012年深化课程改革以来，浙江省高中数学教学内容作了相应调整，原来一些高考必考部分的内容，如导数和概率等，从2015年起调整到选考部分．

1　知识内容

2016年数学高考自选部分包含“复数与导数”和“计数原理与概率”这2个模块．其中复数与导数模块包括的知识内容有:导数的概念与几何意义，基本初等函数的导数公式，导数的运算法则，利用导数求函数的单调性、极值、最大(小)值，复数的概念，复数加、减运算的几何意义，复数的四则运算．计数原理与概率模块包括的知识内容有:加法原理和乘法原理，排列与组合，二项式定理，杨辉三角与二项式系数，事件、事件的关系与运算，互斥、对立、独立事件，概率与频率，古典概型，解决简单的实际问题．

2　命题分析

“18选6”作为浙江省高考的一个特色，其中2个数学模块的考查，内容丰富，考查的知识点多、涉及面广．预计2016年将继续保持每个模块各2个小题的格局，总体难度较之2015年以前应有所降低，更注重主干知识和基本思想方法的考查．

2．1导数

导数及其应用通常围绕3个点进行命题: 1)围绕导数的几何意义展开，设计求曲线的切线方程，根据切线方程求参数值等问题，这类试题在考查导数几何意义的同时也考查导数的运算、函数等知识，试题的难度不大;2)围绕利用导数研究函数的单调性、极值(最值)展开，设计求函数的单调区间、极值、最值，已知单调区间求参数或者参数范围等问题，在考查用导数研究函数性质的同时考查分类与整合思想、化归与转化思想等数学思想方法;3)考查导数在求解函数问题中的应用，涉及应用导数证明不等式问题以及方程等，同时考查逻辑思维能力和分析问题、解决问题的能力．命题的重点是利用导数研究函数的单调性等问题．

2．2复数

主要考查复数的概念、分类，复数的几何意义、复数的运算，特别是复数的乘法与除法运算，求复数的模、复数的虚部、复数在复平面内对应的点的位置等．常常将复数的概念、复数的几何意义和复数的四则运算融合在一起，其中复数的运算、纯虚数的概念以及“分母实数化”是考试的重点．运算时注意“i2=－1”以及运算的准确性．

2．3计数原理

对2个计数原理及排列、组合的考查主要是直接利用计数原理、排列、组合知识进行计数;对二项式定理的考查主要是求展开式中的某一项、某一项的二项式系数、各项系数和等，考查赋值技巧，难度不大．其中与通项公式有关问题的考查是命题的重点．

2．4概率

概率的考查常常结合排列组合知识进行，其中古典概型为命题的重点内容，常与互斥事件、对立事件相结合命题，考查古典概率的计算求解能力和枚举、分类讨论等思想方法．从近几年的命题情况看，概率问题命题的背景通常是摸球问题．

3　典题剖析

分析显然x∈R，对f(x)进行求导，得

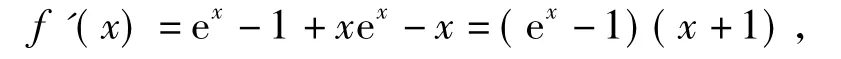
求函数f(x)的单调递增区间，转化为求解不等式f'(x)＞0，即

从而解得函数f(x)的单调增区间为(－∞，－1］和［0，+∞)．

评注利用导数研究函数单调性的步骤:

1)根据函数f(x)的解析式求解其定义域;

2)根据基本初等函数的导数及求导法则求出函数f(x)的导函数f'(x);

3)不等式f'(x)＞0的解集就是函数f(x)的单调递增区间，不等式f'(x)＜0的解集就是函数f(x)的单调递减区间;

4)根据上面的解题过程得出结论．

分析先考虑f(x)的定义域为(0，+∞)，再对f(x)进行求导，得

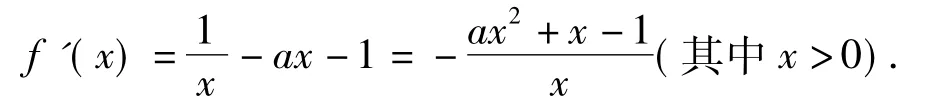
将y=f(x)存在单调递减区间问题转化为f'(x)＜0在(0，+∞)上有解问题，即考虑ax2+x－1＞0 在(0，+∞)上有解，需对a进行分类讨论:

1)当a=0时，x＞1在(0，+∞)上有解;

2)当a＞0时，ax2+x－1＞0在(0，+∞)上总有解;

3)当a＜0时，要使ax2+x－1＞0在(0，+∞)上有解，只需ax2+x－1=0有2个不相等的正实数根，必须

评注已知单调性求参数的取值范围，这里需要对x2的系数a进行分类讨论．当然本题还有另一种常用的解法:通过参数分离，转化为a＞，其中x∈(0，+∞)有解来考虑．

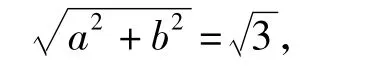
评注复数的考查核心是代数形式的四则运算，即使是概念的考查也需要相应的运算来支持．本题首先根据复数模的定义得复数相乘可根据平方差公式求得

也可根据共轭复数的性质求得

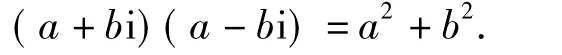
例4复数z满足(z－3)(2－i)=5(其中i为虚数单位)，求z的共轭复数

分析先由(z－3)(2－i)=5，求出

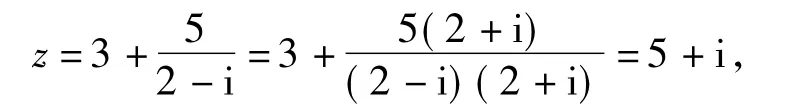
评注复数代数形式的四则运算解题时，只要按照法则进行即可，复数代数形式的运算类似于多项式的运算，加法类似于合并同类项，乘法类似于多项式乘多项式，除法类似于分母有理化(实数化)，分子、分母同乘分母的共轭复数．

再令x=1，得展开式中各项系数之和为(1－2)8=1．

评注二项式定理中最关键的是通项公式，即二项式(a+b)n的展开式的通项公式是Tk+1=求展开式中特定的项或者特定项的系数等均可以利用通项公式和方程思想解决．应用通项公式要注意以下几点:

1)它表示二项展开式的任意项，只要n与r确定，该项就随之确定;

2)Tr+1是展开式中的第r+1项，而不是第r 项;

3)公式中a，b的指数和为n，且a，b不能随便颠倒位置;

4)要将通项中的系数和字母分离开，以便于解决问题;

5)对二项式(a－b)n展开式的通项公式要特别注意符号问题．

例6设(x2+1)(x+1)9=a0+a1(x+2)+ a2(x+2)2+…+a11(x+2)11，求a1+a2+…+a11的值．

分析先求出a0，取x=－2，得a0=－5，再取x=－1，得a0+a1+a2+…+a11=0，最后得到

评注二项展开式的系数和及一些特定项的系数通常是通过对二项式及其展开式中给变量赋予特殊值得出的，注意根据展开式的形式给变量合理赋值．

例7设袋中共有7个球，其中4个红球，3个白球．从袋中随机取出3个球，求取出的白球比红球多的概率．

分析首先明确这是一个古典概型概率问题．从袋中取出3个球，取法共有种，其中白球比红球多的取法有种．因此取出的白球比红球多的概率为

评注解决古典概型概率问题，关键是弄清基本事件的总数n以及某个事件A所包含的基本事件的个数m，然后由公式求出概率;事件A的个数常常用列举法得出，对于较复杂的互斥事件的概率求法可考虑利用分类相加或对立事件去求．

例8袋中有形状、大小都相同的4个球，其中1个白球、1个红球、2个黄球，从中1次随机摸出2个球，求这2个球颜色不同的概率．

分析从4个球中1次随机摸出3个，共有6种摸法，2个球颜色不同的情况相对复杂，可以考虑2个球颜色相同的情况(只有1种)，这样不同的共有5种，因此其概率为

评注求解互斥事件、对立事件的概率问题时，一要先利用条件判断所给的事件是互斥事件，还是对立事件;二要将所求事件的概率转化为互斥事件、对立事件的概率;三要准确利用互斥事件、对立事件的概率公式去计算所求事件的概率．

4　精题集萃

1．设f(x)=a(x－5)2+6lnx，其中a∈R，曲线y=f(x)在点(1，f(1))处的切线与y轴相交于点(0，6)，求函数f(x)的单调区间．

2．已知函数f(x)=(1+x)e－2x，当x∈［0，1］时，求证:

3．若复数z满足iz=2+4i，求在复平面内z对应的点的坐标．

7．袋中共有15个除了颜色外完全相同的球，其中有10个白球，5个红球．从袋中任取2个球，求所取的2个球中恰有1个白球、1个红球的概率．

8．有3个人，每人都以相同的概率被分配到4个房间中的一间，求至少有2人被分配到同一房间的概率．

参考答案

1．解因为f(x)=a(x－5)2+6lnx，所以

令x=1，得

从而曲线y=f(x)在(1，f(1))点处的切线方程为

由点(0，6)在切线上可得

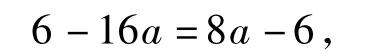
令f'(x)=0，解得x1=2，x2=3．当0＜x＜2或x＞3时，f'(x)＞0，故f(x)在(0，2)，(3，+∞)上为增函数;当2＜x＜3时，f'(x)＜0，故f(x)在(2，3)上为减函数．因此函数f(x)的单调递增区间为(0，2)，(3，+∞)，单调递减区间为(2，3)．

2．证明要证x∈［0，1］时，

记h(x)=(1+x)e－x－(1－x)ex，则

当x∈(0，1)时，h'(x)＞0，h(x)在［0，1］上是增函数，故

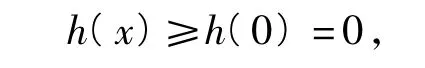
于是f(x)≥1－x，其中x∈［0，1］．要证x∈［0，1］时，

只需证明ex≥x+1．记K(x)=ex－x－1，则

当x∈［0，1］时，K'(x)＞0，因此K(x)在［0，1］上是增函数，故

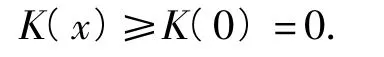
3．解由iz=2+4i，可得

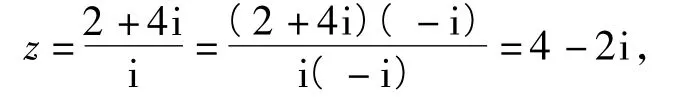
因此z对应的点的坐标是(4，－2)．

4．解

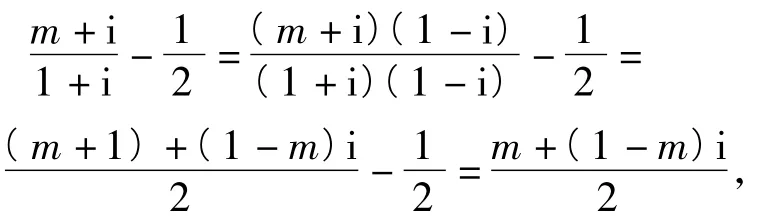
5．解(1+x)2n中x3项的系数为中x3项的系数为2n．由得

解得n=2．

6．解二项展开式通项为

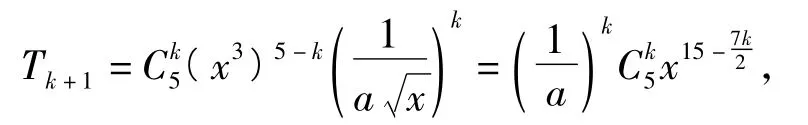
8．解利用对立事件概率的关系．3个人分到4个房间的分法总数是43=64，每间至多只有1人的分法总数为，因此至少有2人被分配到同一房间的概率是