平面解析几何复习策略
2016-05-19胡建烽余姚中学浙江宁波315400
●龚 凤 胡建烽 (余姚中学 浙江宁波 315400)
平面解析几何复习策略
●龚凤胡建烽(余姚中学浙江宁波315400)
1 内容简析
平面解析几何是利用点与有序实数对的一一对应和曲线与方程的一一对应来实现用代数方法研究几何问题或用几何方法研究代数问题的一门学科.解析几何的本质决定了我们要关注曲线的定义、方程以及曲线的性质.高中数学主要研究的曲线有直线、圆与圆锥曲线.从曲线的定义看,圆的定义有定点定长定义、距离之比定义等;圆锥曲线的定义有距离和(差)定义、斜率之积定义和焦点准线的统一定义等,同时我们还要关注这些定义的细节及注意点.从曲线的方程看,我们要关注标准方程推导过程所包含的求轨迹方程的方法,关注不同曲线标准方程的个性化特征以及用方程研究几何问题的程序化方法,如用方程研究曲线的位置关系,用方程研究曲线的范围、曲线的对称性、顶点等.从曲线的性质看,要关注曲线的某些性质与方程的特征有着怎样的必然联系,如离心率、渐近线等特征量对曲线形状的影响,另外,还要特别关注曲线自身的几何性质对简化代数运算的巨大作用.
2 试题分析
平面解析几何作为高中数学的核心内容,在高考中有着举足轻重的地位,一直是高考中的主干题型和必考内容,既有小巧灵活的容易题,也有新颖别致的中等题、压轴大题,其中不少问题的解决对考生的数学思维、运算能力等均有较高要求.直线与圆在高考中主要以选择题或填空题的形式出现,命题重点有2个:1)考查直线方程及2条直线位置关系,常与充要条件内容相结合;2)考查直线与圆、圆与圆的位置关系,解决弦长问题、切线问题,常与三角函数、圆锥曲线等内容相结合.线性规划内容在高考中主要以选择题或填空题的形式出现,命题重点有:简单的规划最值问题,有时会与应用问题相结合;含参规划问题,常与恒成立、有解问题相结合;整点规划问题;与圆等内容相结合的规划问题等.对于圆锥曲线内容的考查,在高考中,试题形式在选择题、填空题以及解答题中均有所体现,其命题重点主要有:1)选择题、填空题和解答题第1)小题重在考查定义、标准方程和几何性质,主要围绕渐近线、离心率等进行题目设置;2)理科解答题主要考查直线与椭圆、抛物线及圆的位置关系,而文科解答题主要考查直线与抛物线、直线与圆的位置关系,不涉及直线与椭圆的位置关系.
3 典题剖析
3.1线性规划
高考对线性规划的考查是对直线方程内容考查的深化,教学中要引导学生掌握快速判定可行域的方法,如教师总结出来的口诀“同则上、异则下”等;引导学生正确理解目标函数的几何意义,如距离、截距、斜率等,再利用恰当的应对策略去解决问题.
A.(1,+∞)B.(0,1)
C.(-1,1)D.(-∞,-1)∪(1,+∞)
(2010年浙江省数学会考试题)
分析易知直线kx-y-2k+1=0过定点(2,1),二元一次不等式y≥kx-2k+1表示直线kx-y-2k+1=0及上方的区域,故要使可行域为三角形区域,直线kx-y-2k+ 1=0需介于y=x-1与x=2之间,于是k∈(1,+∞).
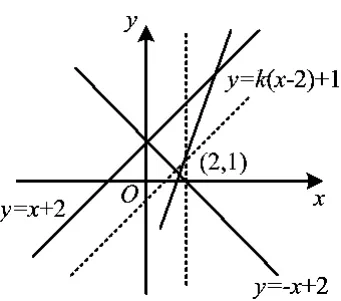
图1
评注该题内容简单,背景熟悉,学生入手容易,但是学生极易选择答案“D”,主要原因是由于学生对“用平面区域表示二元一次不等式(组)”的内容理解不够深刻,对“同侧同号、异侧异号”的认识浮于表面,导致线性约束条件含有参数时的可行区域判断出现问题.
(2014年浙江省数学高考理科试题)
分析此题可以等价转化为求目标函数z= ax+y的最大值、最小值,且满足由于目标函数中含有参数a,如何不重不漏地进行分类讨论以及找到简化讨论的方法,是解决此类问题的关键.
解法1(必要条件缩小范围)先作出可行域,取可行域中的点A(1,0)代入1≤ax+y≤4,得1≤a≤4,此时直线y=-ax+z的斜率-a∈[-4,-1],故z的最大值、最小值分别在点B和点A处取到,即
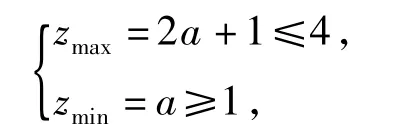
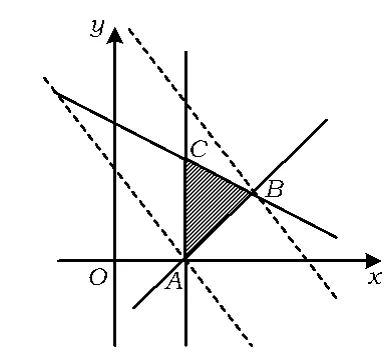
图2


评注含参规划问题是近几年数学高考的热点和难点,在教学中需特别关注以下2点:1)分类讨论前需清楚为何而讨论,若讨论较复杂则考虑用必要条件缩小范围;2)端点代入法确实是解决含参规划问题的一条“捷径”,但是需要注意区分不宜用、甚至不能用的具体情形,否则学生一刀切地“滥用”,效果会适得其反.
3.2直线与圆的方程
直线与圆是2个基本图形,对它们的研究,既可以从几何角度来探索它们的位置关系,又可以利用方程来解决一些度量问题,体现用代数方法解决几何问题的思想.直线与圆方程也是进一步研究圆锥曲线的基础,在每年的高考中均有涉及,除了考查基本概念和基本公式外,还会突出考查弦长问题、切线问题、直线与圆(圆与圆)的位置关系判定等技能与技巧,因此在高三复习中,也需要对这部分内容进行落实并强化.
例3若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是______.
(2015年浙江省数学高考理科试题)
分析解决此题的关键是目标函数“z=|2x+ y-2|+|6-x-3y|”去绝对值的处理.因为x2+ y2≤1表示圆x2+y2=1及其内部的点,可得6-x-3y>0,故目标函数可化为

而直线2x+y-2=0与圆x2+y2=1相交,只需将可行域分成2个部分,再分类讨论去掉绝对值即可解决问题.另外,对于给定的正数z,目标函数

表示平行四边形,故也可以用平行四边形与圆有公共点来解决问题.
解法1(分类讨论去绝对值)
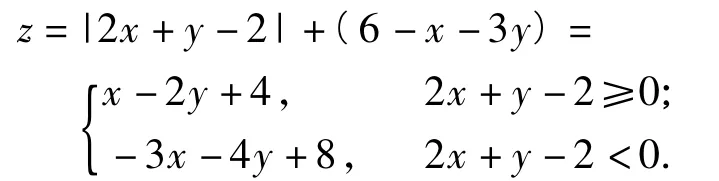
综上所述,|2x+y-2|+|6-x-3y|的最小值是3.

图3

图4
解法2(几何意义数形结合)因为

所以对于给定的正数z,目标函数z=|2x+y-2|+ |6-x-3y|表示平行四边形(如图4所示),求得
解法3(绝对值三角不等式)如图5,在区域1中,


评注本题以直线与圆的位置关系问题为载体,以含有绝对值的规划问题为抓手,考查学生对分类讨论、数形结合和化归等思想的理解.其中,含有绝对值的问题为近几年浙江高考的热点,常见的处理视角有:1)定义分类讨论视角;2)几何意义数形结合视角;3)绝对值三角不等式视角等.在教学过程中需结合具体问题加以关注.

图5

图6
例4如图6,⊙C与x轴相切于点T(1,0),与y轴正半轴交于点A,B(点B在点A的上方),且|AB|=2.
1)⊙C 的标准方程为______;
2)过点A任作一条直线与⊙O:x2+y2=1相交于点M,N,下列3个结论:

其中正确结论的序号是______(写出所有正确结论的序号).
(2015年湖北省数学高考理科试题)
分析本题以双圆为背景,主要考查求圆方程、判断直线与圆的位置关系以及利用圆的方程进行消元代换,体现代数方法解决几何问题的思想.
1)考查基本量的计算,较为容易.已知⊙C与x轴相切于点T(1,0),设C(1,t),由于|AB|=2,则因此所求⊙C的标准方程为


消去x2,得

易知答案应选①②③.
评注本题作为2015年湖北省数学高考理科压轴填空题,虽然有一定的难度,但实际上学生只要不被繁琐的数据吓倒并静下心来仔细计算,同时,适时地利用圆的方程进行消元代换,即可发现距离比值为定值.另外,该题的几何背景为阿波罗尼斯圆,即到定点的距离之比为的点的轨迹为圆x2+y2=1.这是一道源于课本的好题,因此,教师在教学过程中也需要注意对教材的二次开发.
3.3圆锥曲线
教师在对圆锥曲线内容的复习中,除了做好常规工作外,还要关注以下3点:1)焦点、渐近线及抛物线中的“折直互化”;2)常用方法(如设而不求、整体代换等)、常用公式(如弦长公式、抛物线上两点斜率公式等);3)有意识地培养学生数形结合、函数方程等数学思想,鼓励学生进行较复杂的代数运算.
(2015年浙江省数学高考文科试题)
分析本题题意明确、入手容易,学生只需先求出右焦点关于直线的对称点Q的坐标,并代入椭圆方程,即可得到关于a,b,c的等量关系,进而求得离心率.但是,如果选择了此解法,运算量将会非常大,因此需要结合题目,充分利用椭圆的定义与方程,优化解题方法.


图7

图8
解法2如图8,设椭圆左焦点为F',联结QF',则在△OFH中,

故在△QFF'中,

又因为|QF'|+|QF|=2a,所以

评注本题以椭圆为背景,考查了圆锥曲线的定义、标准方程和几何性质.此类问题解决的关键在于将题目中的几何条件翻译成坐标语言,需要学生有较强的运算求解能力.同时,教学过程中要注意对不同翻译方法的对比,指导学生有选择地简化运算,如本题中对“点在椭圆上”的翻译,既可以翻译成坐标满足椭圆方程,也可以用椭圆定义进行刻画.圆锥曲线的定义优先策略往往能起到简化运算的效果,在教学时应予以关注.
例6如图9,已知抛物线C1:x2=y,⊙C2: x2+(y-4)2=1的圆心为点M.若点P是抛物线C1上一点(异于原点),过点P作⊙C2的2条切线,交抛物线C1于点A,B,若过点M,P的直线l垂直于AB,求直线l的方程.
(2011年浙江省数学高考理科试题)
分析本题涉及到直线、圆、抛物线,有一定难度.学生解题时常会遇到无法下手、无法翻译和无法计算等困难,这其实也是学生解决解析几何问题的普遍问题.如何破解上述难关成为提高解析几何教学效果的关键.

图9
解法1(线参法)设P(t,t2),过点P且与⊙C2相切的直线为
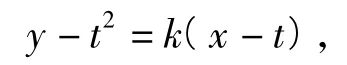
化简得
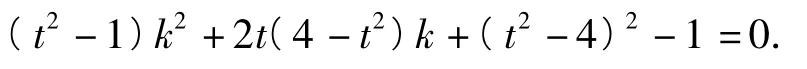
设A(x1,y1),B(x2,y2),直线PA,PB的斜率分别为k1,k2,则

联立y-t2=k1(x-t)与x2=y,解得x1=k1-t,
由MP⊥AB,得kMPkAB=-1,解得,因此直线l的方程为


所以直线PA的方程为y=(x1+t)x-x1t.因为直线PA与圆相切,所以

化简得
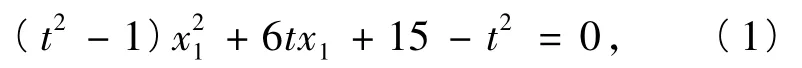
同理可得
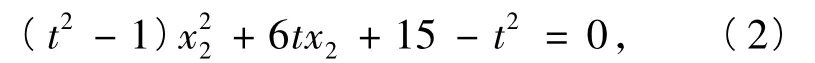
由式(1)和式(2)可知,x1,x2是方程(t2-1)x2+ 6tx+15-t2=0的2个根.又因为PM⊥AB,所以

评注解法1的关键是设点P及过点P的直线使之成为圆的切线,得到一个十分关键的关系式后施行“设而不求”的方法使题目得到解决;解法2从设抛物线上的3个动点开始,利用直线与圆相切及线线垂直的条件建立3个关系式解方程组,其中用到类比和“设而不求”的方法.
其实,为破解难关,解决解析几何问题往往可按照如下步骤进行:
1)明逻辑:把握好题目内在的逻辑,有助于把握住解题方向,并迅速找到解题突破口;
2)巧设参:一般情况下,以问题的起点作为设参的依据,要注意选择何种方程,即点斜式、斜截式、截距式、点斜式变异体等的选择;
3)准翻译:在对比、选择的过程中积累常见的几何条件的翻译方法,如垂直、中点、中垂线、等腰三角形、弦长、切线、面积、圆上(内、外)等,在有多种翻译方法时需选择最佳途径;
4)巧代换:把握住2种代换方式:“设而不求”和“设而要求”,并进一步体会“设而不求”和“设而要求”的内涵;
5)细运算:俗话说“百闻不如一练”,鼓励学生亲力亲为,扎实提升运算能力,强化解题基本功.
4 精题集萃
1.在平面直角坐标系xOy中,已知向量a,b, |a|=|b|=1,a·b=0,点Q满足曲线,其中0≤θ≤2π},区域,其中r<R}.若C∩ Ω为2段分离的曲线,则()
A.1<r<R<3B.1<r<3≤R
C.r≤1<R<3D.1<r<3<R
2.已知P1(a1,b1)与P2(a2,b2)是直线y= kx+1(其中k为常数)上2个不同的点,则关于x, y的方程组的解的情况是()
A.无论k,P1,P2如何,总是无解
B.无论k,P1,P2如何,总有唯一解
C.存在k,P1,P2,使之恰有2个解
D.存在k,P1,P2,使之有无穷多解
3.在等腰△ABC中,AB=AC,AC边上的中线BD长为6,则当△ABC的面积取得最大值时,AB的长为______.
4.已知⊙C:(x-3)2+(y-4)2=1和点A(-m,0),B(m,0)(其中m>0),若⊙C上存在点P,使得∠APB=90°,则m 的最大值为______.
5.已知⊙O:x2+y2=1和点A(-2,0),若定点B(b,0)(其中b≠-2)和常数λ满足:对⊙O上那个任意一点M,都有|MB|=λ|MA|,则b= ______,λ=______.
7.已知抛物线C:x2=4y的准线与y轴交于点M,过点M斜率为k的直线l与抛物线C交于点A,B,线段AB的中垂线与y轴交于点D(0,a).
1)求实数a的取值范围.
2)是否存在这样的实数k,使得抛物线C上总存在异于A,B的点Q(x0,y0),满足点Q在以AB为直径的圆上,若存在,求k的取值范围;若不存在,说明理由.
1)求证:PA⊥PB;
2)设PA,PB与x轴分别交于点M,N,求△PMN面积关于y0的函数表达式S(y0).
参考答案
1.A2.B
