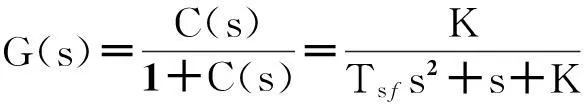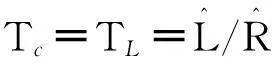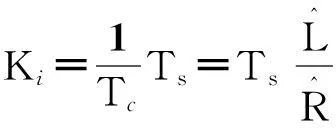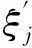UUV推进电机在线参数辨识自适应控制方法研究
2016-05-16刘彦呈刘厶源王川郭昊昊任俊杰于盈
刘彦呈, 刘厶源, 王川, 郭昊昊, 任俊杰, 于盈
(1.大连海事大学 轮机工程学院,辽宁 大连 116026;2.大连航标处 交通运输部北海航海保障中心,辽宁 大连 116001)
UUV推进电机在线参数辨识自适应控制方法研究
刘彦呈1,刘厶源1,王川1,郭昊昊1,任俊杰1,于盈2
(1.大连海事大学 轮机工程学院,辽宁 大连 116026;2.大连航标处 交通运输部北海航海保障中心,辽宁 大连 116001)
摘要:针对水下无人航行器(UUV)的推进电机矢量控制系统中电流控制器性能因参数变化而下降的问题,提出一种基于智能在线参数辨识的电流环自适应控制方法。以离散型永磁同步推进电机动态模型作为被控对象,采用动态惯性权重粒子群算法对永磁同步推进电机的定子电阻和dq轴电感进行在线辨识,根据电流控制器工程设计方法,将辨识所得的电机参数实时用于计算电流控制器的PI值,实现电流环的自适应控制。最后,通过仿真实验验证所提方法的有效性,结果表明该方法可以有效地克服水下快速洋流对推进电机的负载扰动,进而实现永磁同步推进电机的快速、高精确度电流控制性能。
关键词:水下无人航行器;永磁同步推进电机;矢量控制;粒子群算法;参数辨识;自适应控制
0引言
水下无人航行器(unmanned underwater vehicle,UUV)作为海洋资源开发和海洋军事领域应用不可缺少的工具,相比于载人航行器和带缆航行器,UUV有着安全系数高、造价低、尺寸小、重量轻、灵活性高、活动范围广等独特优势。UUV能够在水中进行长期观察、探测和打捞作业,可被广泛应用于众多领域。在军事领域,作为未来海洋战争的一种新型现代化高科技装备,在反潜、反雷、海上封锁和反封锁等方面都有着重要的用途;在科学领域,UUV可进行水文调查、海洋勘测和海洋观测;在经济领域,UUV对于石油开采、海底电缆的检测、港口建设、水下施工、海洋救援、打捞船只以及海底地形探测等方面也都有着巨大的作用。
电力推进作为UUV的主推进方式,是由直流供电系统提供电能驱动电机带动螺旋桨旋转,进而驱动UUV运动。永磁同步电机(permanent-magnet synchronous motor,PMSM)以其体积小、结构简单、运行可靠、效率高、损耗低等优点,在数控机床、电动汽车、机器人和电力推进船舶等方面获得了广泛应用[1]。 UUV主要采用永磁同步推进电机(permanent magnet synchronous propulsion motor,PMSPM)作为主推进电机,其转子转速和定子电流的非线性高耦合决定了系统的强非线性,特别当系统存在不确定性时,PMSPM的非线性使得系统很难得到高精确度的控制性能。
在矢量控制系统中,电流环是调速系统中响应最快的一环,其控制器参数的准确性至关重要,这将直接影响到整个调速系统的性能,而电流控制器的参数主要由推进电机的定子电阻和dq轴电感决定。推进电机在不同工况下电流的变化所产生的磁路饱和程度不同,dq轴电感值也会相应发生变化。由于涡流和磁滞引起温度变化时,定子电阻和永磁体磁链也会随之变化[2],这些参数将导致电流控制器PI参数与实际运行条件不匹配,导致系统性能明显下降。因此,对推进电机参数进行准确的辨识将直接决定电流控制器控制性能的好坏,进而影响到整个系统的性能[6]。
本文提出一种动态惯性权重粒子群算法对PMSPM的定子电阻、dq轴电感及永磁体磁链进行在线辨识,将辨识的电机参数送入电流控制器PI参数的计算表达式,对PI参数进行实时整定,以解决PMSPM负载突变时电流控制器PI参数与电机参数匹配问题。
1PMSPM数学模型
假设电动机的电流为三相对称正弦波电流,在忽略电机铁心饱和,不计电机中的谐波、涡流和磁滞损耗的前提下,PMSPM在转子同步旋转坐标系中的数学模型为[4-5]

(1)
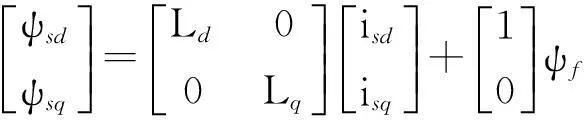
(2)
Te=npψfiq。
(3)
式中:usd、usq、isd、isq、Ld、Lq、ψsd、ψsq分别为同步旋转dq坐标系中定子线圈的电压、电流、电感和磁链;Rs为定子绕组每相电阻;np为极对数;Ωr为电机转子旋转电角速度;ψf为永磁体转子产生的磁链幅值;p为微分算子。
为了方便起见,将待辨识参数记为
ξ=[ξ1ξ2ξ3ξ4]。
将式(1)、式(2)中的PMSPM模型离散化处理,可得离散状态方程:
(4)
式中:ts表示采样周期,k表示第k次采样。

(5)
2粒子群优化算法
粒子群(particle swarm optimization,PSO)算法是Kennedy博士和Eberhart博士于1995年提出的一种演化计算技术[9],其源于对群体动物觅食行为的模拟,是一种全局优化进化算法,最初用于处理连续优化问题,目前已经可以用于解决大量非线性,不可微和多峰值的复杂问题优化,并已经广泛用于科学和工程领域。
2.1标准粒子群算法
标准粒子群算法(standard particle swarm optimization,SPSO)首先初始化N个随机粒子以一定的速度在D维空间中运动,并经过逐迭代找到最优解。假设第i个粒子在空间中的位置为xi=(xi1,xi2,…,xid),其运动速度为vi=(vi1,vi2,… ,vid),该粒子所经历的个体最优解为pi=(pi1,pi2,…,pid),群体中所有粒子的全局最优解为pg=(pg1,pg2,…,pgd)。其中,1≤i≤N,1≤d≤D。在每一次迭代过程中,粒子通过跟踪当前找到的两个最优解,并根据式(6)、式(7)来更新自己的速度和位置。
vi(k+1)=ωvi(k)+c1r1[pi(k)-xi(k)]+
c2r2[pg(k)-xi(k)],
(6)
xi(k+1)=xi(k)+vi(k+1)。
(7)
其中:ω是惯性权重,通常取值为(0,1)之间的随机数;c1和c2是学习因子;r1和r2分别是个体极值和全局极值间的均衡因子,通常取值为[0,1]之间的随机数。
2.2动态惯性权重粒子群算法
在PSO算法中,影响算法性能的主要因素有两个:一个是粒子进化速度,另一个是粒子聚集度。惯性权重ω作为最重要的一个参数,其作用是在保持原有粒子多样性的同时保证全局和局部搜索性能的均衡。对于复杂的非线性系统优化过程,粒子群的进化速度和聚集程度的不断变化会导致惯性权重随之变化。因此,为了保证算法的全局和局部搜索性能,引入了进化速度因子和聚集度因子,提出动态惯性权重粒子群算法(dynamic inertia weight particle swarm optimization,DIWPSO),从而解决非线性系统优化过程后期粒子缺乏多样性、全局搜索能力不足,易陷入局部最优值等问题。
全局最优值取自于个体最优值,其变化取决于个体最优值的变化,同时也反映了粒子群中所有粒子的整体运动效果。在搜索过程中,当前迭代的全局最优值总是要优于或等于上一次迭代的全局最优值。根据上述原理,通过对当前最优值和上一次迭代的最优值进行比较,以两者之比作为速度进化因子。
考虑到优化过程中存在寻找极大值或极小值两种情况,具体地,若优化目标是寻找极大值,F(pgT)≥F(pgT-1),则定义进化速度因子h=F(pgT-1)/F(pgT);若优化目标是寻找极小值,F(pgT)≤F(pgT-1),则定义h=F(pgT)/F(pgT-1)。综合上述两种情况,将进化速度因子h定义为

(8)
其中:F(pgT)和F(pgT-1)分别为当前和上一次迭代的全局最优值。该参数不但考虑了算法运行的历史,还反映了粒子群整体进化速度,即h值越小,粒子进化速度越快。当经过了一定的迭代次数之后,h值保持为1,则断定算法停滞或者找到了最优解。
在PSO算法中,无论是早熟收敛还是全局收敛,全局最优值总是优于所有个体的当前的适应度值,粒子都会出现“聚集”现象。因此,粒子的聚集度是影响算法性能的重要因素,也是反映粒子多样性的重要指标。
设Fave为所有粒子当前适应度值的平均值,表达式为

(9)


(10)
其中,F(pgT)为当前全局最优值。该参数反映了所有粒子当前的聚集程度,同时在一定成都上也反映出粒子的多样性。g值越大,粒子群聚集程度也越大,粒子多样性越小。当g=1时,粒子群中的所有粒子具有同一性,如果此时算法陷入局部最优,则结果不容易跳出该局部极点。
ω=f(h,g)。
(11)
如果粒子进化速度较快,算法可以在较大的搜索空间内持续搜索,粒子就可以保持大范围的寻优。当粒子群进化速度减慢时,可以减小ω的值,使得粒子群在小空间内搜索,以便更快地找到最优解。若粒子较分散,粒子群就不易陷入局部最优解。随着粒子群的聚集程度的提高,算法易陷入局部最优,此时应增大粒子群的搜索空间,提高粒子群的全局寻优能力。综上所述,ω应该随着粒子的聚集度的升高而增大,随着进化速度的降低而减小,它可以表示为
ω=ω0-hωh+gωg。
(12)
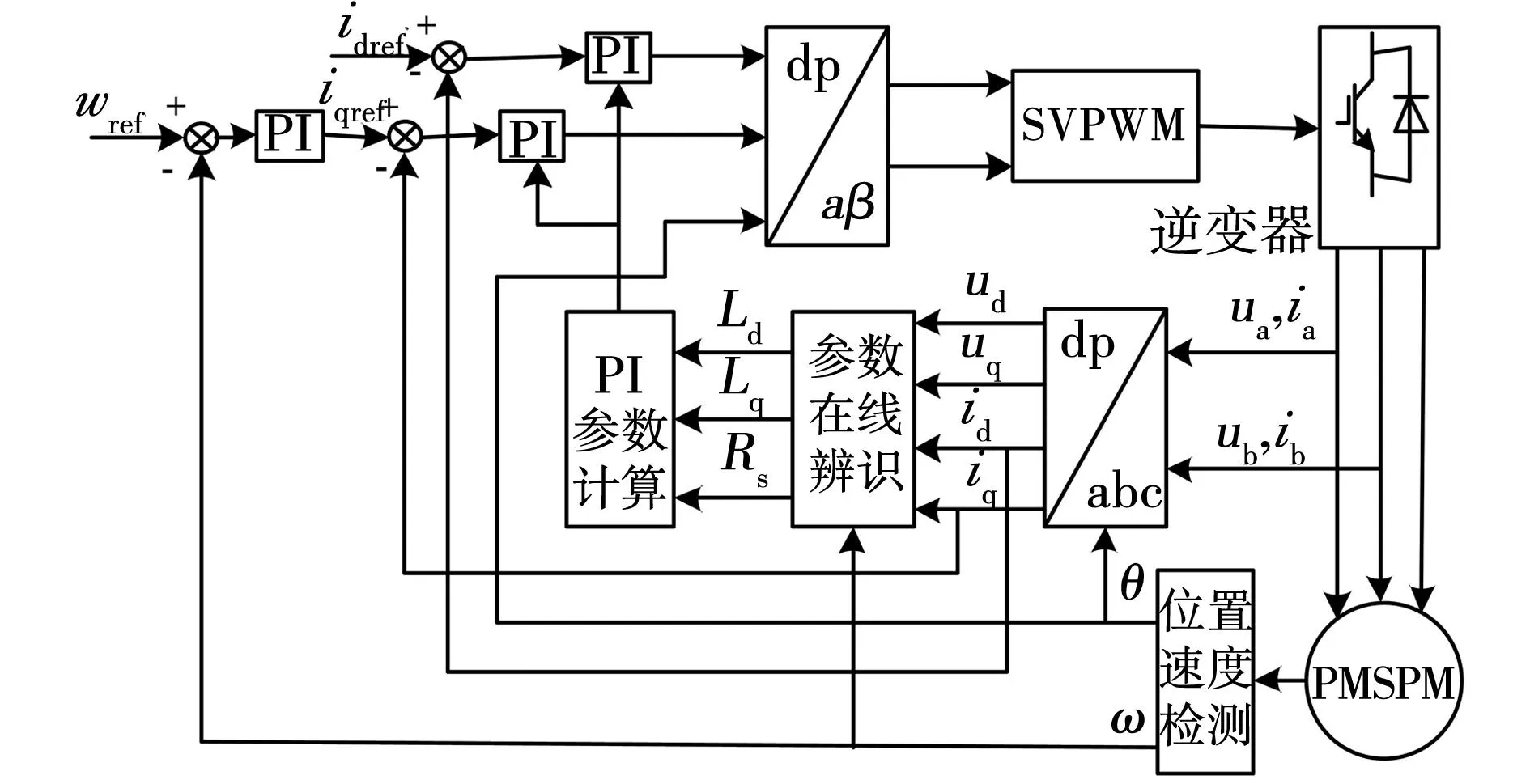
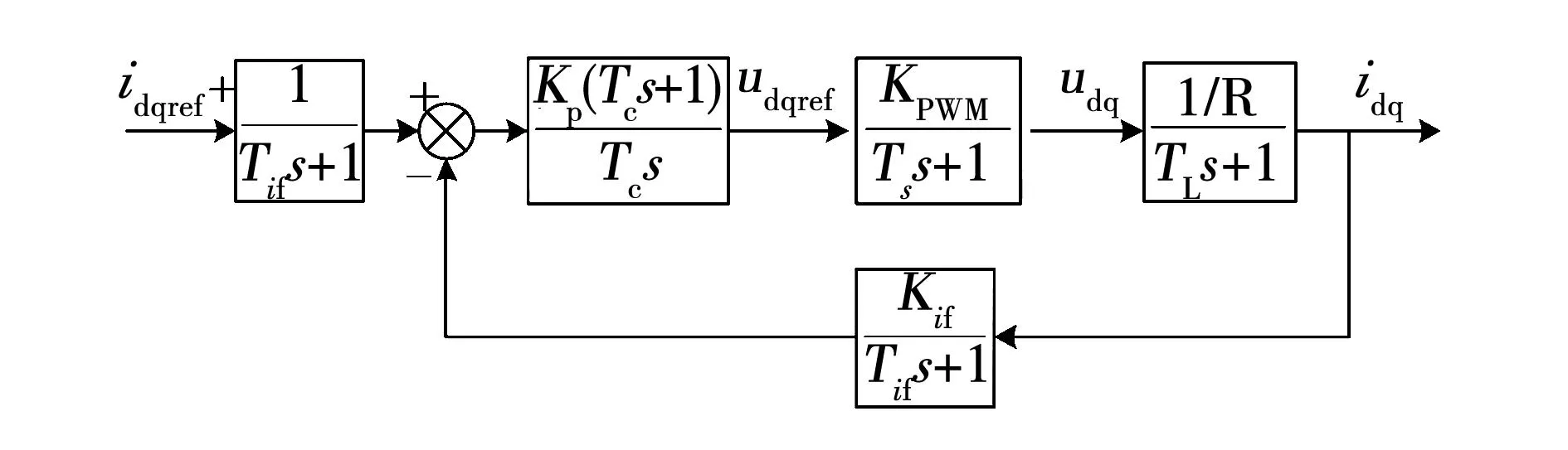
式中:ω0为ω的初始值,通常ω0=1。由于0 DIWPSO算法在运行过程中通过更改h和s的值来动态调节,从而改进算法的性能。初始状态下,置h=0,g=0,则DIWPSO算法步骤如下: 步骤1:对随机粒子进行位置、速度向量的初始化,计算各粒子的适应度。 步骤2:对搜索空间中的全局最优值pg和个体最优值pi进行初始化。 步骤3:在迭代过程中,如果满足算法收敛准则或者达到最大迭代次数nmax,则执行步骤7,否则执行步骤4。 步骤4:对搜索空间中的所有粒子的位置和速度进行更新,并计算相应粒子的适应度,进而更新所有粒子中的全局最优值pg和个体最优值pi。 步骤5:根据式(8)、式(10)和式(12),分别计算进化速度因子h、聚集度因子g和惯性权重w。 围术期疼痛管理是麻醉学走向围术期医学的重要组成部分,其管理模式正在从以“联合阿片类药物与NSAIDs药物为主”转变为“联合区域神经阻滞与NSAIDs药物” 为主。麻醉科医师须在现有研究证据的基础上,进一步改进临床行为,积极践行更理想的多模式镇痛理念,以大幅提升中国围术期患者疼痛管理数量与质量以及患者远期预后。 步骤6:将迭代数加1,循环重复执行步骤3。 步骤7:输出全局最优值pg,算法结束。 3自适应电流环控制 3.1电流控制器设计 PMSPM采用自适应矢量控制系统如图1所示,通过独立控制d轴励磁电流分量和q轴转矩电流分量来控制电流控制器,进而得到的dq轴控制电压ud和uq,经过SVPWM调制对逆变器的高频输出电压进行控制,从而驱动PMSPM。 图1 PMSPM自适应矢量控制系统框图Fig.1 PMSPM adaptive vector control diagram 电流控制器参数一般只与逆变器和电机的参数有关,不受外部负载影响,所以电流环有其固定的结构,电流控制器的参数可以按一定方法计算得到。由于PI调节器可以消除反电势常数扰动造成的静差,具有较好的抗扰动能力,因此PMSPM采用PI控制,其电流环结构原理如图2所示[3]。 图2 电流环结构原理图Fig.2 Schematic diagram of current loop structure 图2中idqref、udqref分别为dq轴参考电流和参考电压。电机的电枢回路中存在电阻R和电感L,可看作一阶惯性环节。TL为电磁时间常数,TL=Ldq/Rs。同理可将PWM逆变器看作具有时间常数Ts的一阶惯性环节,Ts=1/fs,fs为逆变器开关元件的工作频率。KPWM表示逆变器的放大倍数,Tif为电流反馈通道的滤波时间常数,Kif为电流反馈系数。电流环开环传递函数为 (13) 由于通常情况下Ts和Tif的值远小于电机的电磁时间常数TL,故用一个时间常数为Tsf的一阶环节来近似代替时间常数为Ts和Tif的小惯性群,电流环的开环传递函数可化简为 (14) 在电流控制器设计中,需用控制器零点与被控对象中较大的时间常数极点相互抵消,以便校正成典型I型系统,而TL>>Tsf,故积分时间常数Tc=TL=L/R,开环传递函数为 (15) 由开环传递函数可知,该系统的电流环闭环传递函数可表示为典型二阶系统 (16) 由工程最佳整定方法“模最佳系统”的参数关系可知KTif=0.5[7],即 (17) 得到PI调节器的比例系数为 (18) 积分时间常数为 (19) 然后再将其按增量式PI调节器算法数字化,可得其积分系数为 (20) 其中,带“^”的参数为辨识值。上述推导说明电流环PI参数值与电机的电感和定子电阻相关。由此可知,在运行条件发生变化时,只要对电机参数进行实时辨识,就能够实时得到电机的PI参数值。 3.2PMSPM在线参数辨识 对于PMSPM系统而言,参数辨识的过程可看作是一个寻优过程,其基本思想是通过实时采集PMSPM的实际三相输出电流,经过坐标变换得到dq轴定子电流isd、isq,同时实时估算PMSPM电气模型的输出电流,将实际电流与估算电流差方和的多次计算均值作为DIWPSO的适应度评估函数,通过DIWPSO算法对PMSPM电气模型不断修正和调整,辨识出实际PMSPM的全部参数,参数辨识原理框图如图3所示。 基于PSO算法的基本思想,PMSPM参数辨识问题可描述成求解适应度函数的优化问题[8]。设从t0至t时间段的采样个数为N,适应度函数可设计为 (21) 图3 参数辨识原理框图Fig.3 Schematic diagram of parameter identification 4实验结果及分析 由于UUV在航行过程中会受到水下复杂流场的影响,对推进电机而言,相当于增加推进电机的负载扰动,因此本实验以负载的突卸和突加为实例,模拟UUV突遇快速洋流的工况,进而研究推进电机的运行状态变化过程。实验平台原理图如图4所示,一台永磁同步推进电机(参数见表1)和一台异步负载电机通过同轴连接器进行机械连接组成系统基础框架。永磁同步推进电机和异步负载电机均采用转子磁场定向矢量控制。为了准确测试UUV推进电机性能,永磁同步推进电机采用转速控制方式,异步负载电机采用转矩控制方式。 图4 UUV推进电机参数自适应控制实验平台Fig.4 Experiment platform for parameter adaptive control of UUV propulsion motor PMSPM参数数值定子电阻Rs/Ω2.879d轴电感Ld/mH8.5q轴电感Lq/mH8.7永磁体磁链ψf/Wb2.56 实验中DIWPSO算法的最大迭代次数nmax为2 000代,粒子数为50,辨识参数的变化范围为实验参数的±100%。参数在线辨识过程如图5所示,从图中可清楚看到,电机各参数均在0.25 s内收敛到稳定状态。 图5 基于DIWPSO算法的PMSPM参数辨识结果Fig.5 PMSPM identified parameters based on DIWPSO algorithm 考虑到控制器参数对于电机参数的敏感度极高,故采用平均误差率对所得辨识参数精准度进行评估。平均误差率是通过计算辨识nmax次的总体误差与nmax之比的百分比得到的。总体误差公式为 (22) 平均误差率公式为 (23) 表2 辨识参数平均误差率 图6、图7分别是采用所提出的自适应算法和基于模型的传统算法对负载电机进行突加和突卸负载时的实验结果,其中负载作用的时间为100 ms,突加和突卸的负载转矩分别为4 N·m和-4 N·m。图6(a)和图7(a)分别为所提出的自适应方法和传统方法的q轴电流变化波形。在负载突加实验过程中,随着电流的增加,电感有下降的趋势[10-11],且实际PI参数值中的比例系数应该减小,积分系数应该变大,但传统的方法PI参数并没有发生变化,相对来说就是比例系数Kp偏大,等效为系统阻尼比变小,就导致电流超调变大,产生较大振荡。反之,负载突卸实验亦然。图6(b)和图7(b)为两种方法的输出转矩变化波形。由式(3)可知,输出转矩与q轴电流成正比关系,因此其波形变化趋势与q轴电流变化波形相同。图6(c)和7(c)分别为采用所提出的自适应方法和传统方法的电机转速变化波形。在矢量控制系统中,电流环作为控制内环,其控制器的鲁棒性将直接影响速度外环控制器的鲁棒性。通过自适应调节电流控制器参数减少电流超调,使得转速超调随之降低。 从图6、图7中可以清楚的发现,在突加和突卸负载时,PMSPM采用自适应方法后电流超调量有明显的缩减,电流变化平稳,表明该方法对于负载扰动有明显的抑制和修正作用。 图6 自适应算法的响应波形Fig.6 Waveform of current algorithm 图7 传统算法的响应波形Fig.7 Waveform of traditional algorithm 5结论 本文提出一种动态惯性权重调整粒子群优化算法用于永磁同步推进电机参数辨识,分析了永磁同步推进电机矢量控制系统中电流环结构并推导出电流环PI参数值计算表达式,利用辨识所得参数实现 控制系统电流环PI参数的实时更新和校正。仿真与实验表明该方法是可行的,且此控制策略可用于负载转矩变化频繁的实际场合,具有较强的鲁棒性及快速响应性。 参 考 文 献: [1]唐任远.现代永磁电机理论与设计[M].北京: 机械工业出版社,1997. [2]WU M L,HUANG S H.Nonlinear parameters identification of PMSM[J].Transactions of China Electrotechnical Society,2009,24(8): 65-68. [3]MACRO T,FRANCESCO P,ZHANG D Q.Real-time gain tuning of PI controllers for high-performance PMSM drives[J].IEEE Transactions on Industry Applications,2002,38(4): 1018-1026. [4]REN J J,LIU Y C,ZHAO Y T,et al.Research on the different vector control schemes with larger power marine PMSM[J].Electric Machines and Control,2011,15(5): 32-37. [5]PRAGASEN P.,KRISHNAN R.Modeling of permanent magnet motor drives[J].IEEE Transactions on Industry Electronics,1988,35(4): 537-541. [6]KHWAJA M,SILVA H.Identification of machine parameters of a synchronous motor[J].IEEE Transactions on Industry Applications,2005,41(2): 557-565. [7]JIAO Z Q,QU B D.PID parameters optimization of PMSM servo system using genetic algorithm[J].Electric Machines & Control Application,2007,34(7): 34-37. [8]LANKARANY M,REZAZADE A.Parameter estimation optimization based on genetic algorithm[J].IEEE Transaction on Industry Applications,2006,36(6): 365-370. [9]WANG C,LIU Y C,ZHAO Y T.Application of dynamic neighborhood small population particle swarm optimization for reconfiguration of shipboard power system[J].Engineering Applications of Artificial Intelligence,2013,26(4): 1255-1262. [10]LI S H,LIU Z G.Adaptive speed control for permanent magnet synchronous motor system with variations of load inertia[J].IEEE Transactions on Industrial Electronics,2009,56(8): 3050-3059. [11]冯江华,桂卫华,许峻峰.考虑参数变化的永磁同步电动机弱磁控制研究[J].微电机,2008,41(4): 28-31. FENG J H,GUI W H,XU J F.Flux-weakening control research of permanent magnet synchronous machines considering parameters variation[J].Micromotors,2008,41(4): 28-31. (编辑:贾志超) Research on online parameter identification and adaptive control of UUV propulsion motor LIU Yan-cheng1,LIU Si-yuan1,WANG Chuan1,GUO Hao-hao1,REN Jun-jie1,YU Ying2 (1.Marine Engineering School,Dalian Maritime University,Dalian 116026,China;2.Dalian Navigation Mark,The Ministry of Transport Beihai Maritime Security Center,Dalian 116001,China) Abstract:In vector control system of unmanned underwater vehicle (UUV) propulsion motor,due to the changes in motor parameters,current controller performance will decline.An adaptive control of permanent magnet synchronous propulsion motor current-loop based on online parameter identification is proposed.The stator resistance and dq axis inductance of the discrete dynamic of permanent magnet synchronous propulsion motor are identified by using the dynamic inertia weight particle swarm optimization,and then by the engineering procedures of the current controller,the identified motor parameters are utilized to dynamically calculate the PI value of current controller to achieve the adaptive control of current loop.Finally,the effectiveness of the proposed scheme is verified by the simulation experiments,and it follows from the results that the proposed scheme can effectively overcome the load disturbance caused by fast ocean currents such that the rapid and high precision current control performance of permanent magnet synchronous propulsion motor is achieved. Keywords:UUV; permanent magnet synchronous propulsion motor; vector control; particle swarm optimization; parameter identification; adaptive control 中图分类号:TM 351 文献标志码:A 文章编号:1007-449X(2016)04-0034-07 DOI:10.15938/j.emc.2016.04.005 通讯作者:刘厶源 作者简介:刘彦呈(1963—),男,博士,教授,博士生导师,研究方向为船舶智能系统控制及自动化、先进运动控制系统; 基金项目:国家自然科学基金(51479018);中央高校基本科研业务费专项资金(313201432) 收稿日期:2014-04-10 刘厶源(1990—),男,博士研究生,研究方向为船舶推进电机控制及其运动控制; 王川(1985—),男,博士,讲师,研究方向为电力系统建模及其稳定性、智能电网技术; 郭昊昊(1984—),男,硕士,助教,研究方向为电机运动控制建模; 任俊杰(1984—),男,博士研究生,研究方向为船舶电力推进大功率永磁电机运动控制技术; 于盈(1979—),女,高级工程师,研究方向为船舶电气自动化。