贯流式水轮发电机空载电压波形畸变与阻尼条损耗发热抑制

范镇南，　韩力，　廖勇，　董秀成，　王军

(1.西华大学 电气与电子信息学院，四川 成都 610039；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400030)



贯流式水轮发电机空载电压波形畸变与阻尼条损耗发热抑制

范镇南1,2，韩力2，廖勇2，董秀成1，王军1

(1.西华大学 电气与电子信息学院，四川 成都 610039；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400030)

摘要:为改善水轮发电机电能质量，预防阻尼绕组过热，保证机组与电网运行安全，基于电机电磁场、电路及传热学理论，建立了水轮发电机三维分层非线性时变运动电磁场-电路结合模型与磁极系统三维稳态温度场模型。进而针对一台的36 MW贯流式机组的128种结构设计方案，通过电磁场-温度场综合计算，广泛深入地分析了定转子槽距比、定子斜槽程度以及每极阻尼条根数等结构参数对空载电压波形畸变率和额定工况阻尼绕组损耗发热的影响，在此基础上，讨论了同时抑制空载电压波形畸变率与阻尼绕组损耗发热的设计措施。计算结果与实测数据相吻合。

关键词:贯流式水轮发电机；空载电压波形畸变；阻尼绕组损耗与发热；电磁场；温度场

0引言

由电压谐波引发的空载电压波形畸变，可能对水轮发电机电能质量与并网运行安全造成不利影响。作为水轮发电机的重要组成部分，阻尼绕组是发电机与电网安全稳定运行的重要保障。在发电机设计阶段，定转子槽距比、每极阻尼条根数、以及定子斜槽等结构参数的选取，不但影响着阻尼绕组损耗发热分布，还对空载电压波形有着密切影响。特别是对于近年在低水头大流量电站广泛应用的贯流式水轮发电机而言[1]，在其设计制造与运行中，不但面临电压谐波导致空载电压波形畸变的难题，还屡次在额定负载工况下发生阻尼条过热故障[2]。为改善贯流式水轮发电机电能质量，预防阻尼绕组过热断条故障，保证运行安全，很有必要采用电磁场与温度场综合分析方法，针对其空载电压波形畸变率与阻尼绕组损耗发热抑制问题，进行全面深入的研究。

在水轮发电机空载电压波形分析与优化方面，早期文献多采用电磁场解析法或电路磁路法进行研究[3-7]。其中，文献[3-6]着重研究了发电机附加磁场与谐波电动势的解析计算；文献[7]则在上述文献成果的基础上，较为全面地分析了增大气隙、采用分数槽绕组、采用定子斜槽或转子斜极、改善极靴表面形状、移动磁极位置、改变阻尼绕组几何形状等方法对空载电压波形的改善效果。以上解析方法具有概念清晰，便于工程人员理解的优点，然而由于难以考虑铁磁材料饱和、定子斜槽、转子旋转及阻尼条涡流等因素的影响，其定量计算的精确度尚有较大提升空间。为克服上述缺陷，近年来，国内外研究者多使用数值计算方法，开展水轮发电机空载电压波形分析研究，取得了较大进展[8-13]。文献[8-9]通过建立凸极同步发电机的运动电磁场时步有限元计算模型，研究了空载电压波形。文献[10]将解析法与有限元方法相结合，计算分析了叠片式凸极同步发电机的空载电压波形，并初步讨论了阻尼绕组偏心0.25倍定子节距对空载电压波形质量的影响。文献[11]将多回路法与电磁场有限元法相结合，用于求解凸极同步发电机电压波形。文献[12]通过建立水轮发电机二维场路耦合时步有限元计算模型，分析了不对称磁极设计方案对空载电压波形的优化效果。

针对阻尼绕组电流、损耗与发热计算问题，文献[13]将阻尼绕组电路网络分析与解析法建模相结合，研究了阻尼条电流波形。文献[14]通过建立凸极电机谐态电磁场有限元计算模型，分别求解了暂态和稳态阻尼条电流。文献[15]将水轮发电机静态电磁场与谐态电磁场有限元模型结合使用，求解了阻尼条损耗。文献[16]应用运动电磁场时步有限元模型，计算了水轮发电机额定与负序工况下的阻尼条电流与损耗。文献[17]使用三维等参元模型，计算了水轮发电机转子稳态温度场。文献[18]基于流场-温度场模型，研究了转子的气体流动和发热情况。

文献[19]综合运用二维运动电磁场有限元模型与三维温度场模型，初步探讨了不同结构与材料参数对阻尼绕组损耗发热的影响。在此基础上，文献[20]通过建立分层运动电磁场模型与三维温度场模型，针对5种定转子槽距比方案与1种定子斜槽方案，开展了空载波形与阻尼绕组损耗发热计算分析。但上述两篇文献所讨论的设计方案较为有限，其研究广度和深度尚待进一步提高。

1电磁场计算模型

1.1发电机基本参数

作为算例的贯流式水轮发电机型号为SFWG36- 72/7350，其基本参数见表1。

表1　发电机基本参数

选定以下4类共128种结构设计方案进行研究，其编号及含义见表2，nb为每极阻尼条根数，其中t1为定子齿距，并保持不变，t2为转子阻尼绕组节距，可调节，t2/t1为定转子槽距比，Δt2/t1为槽距比变化步长。Δskew为定子斜槽程度变化步长。

表2　结构设计方案

1.2运动电磁场边值问题

根据磁场分布的周期性，选定1对磁极的范围作为发电机电磁场的求解区域，并沿轴向将该发电机分为12段，以便准确分析斜槽方案，参见图1。

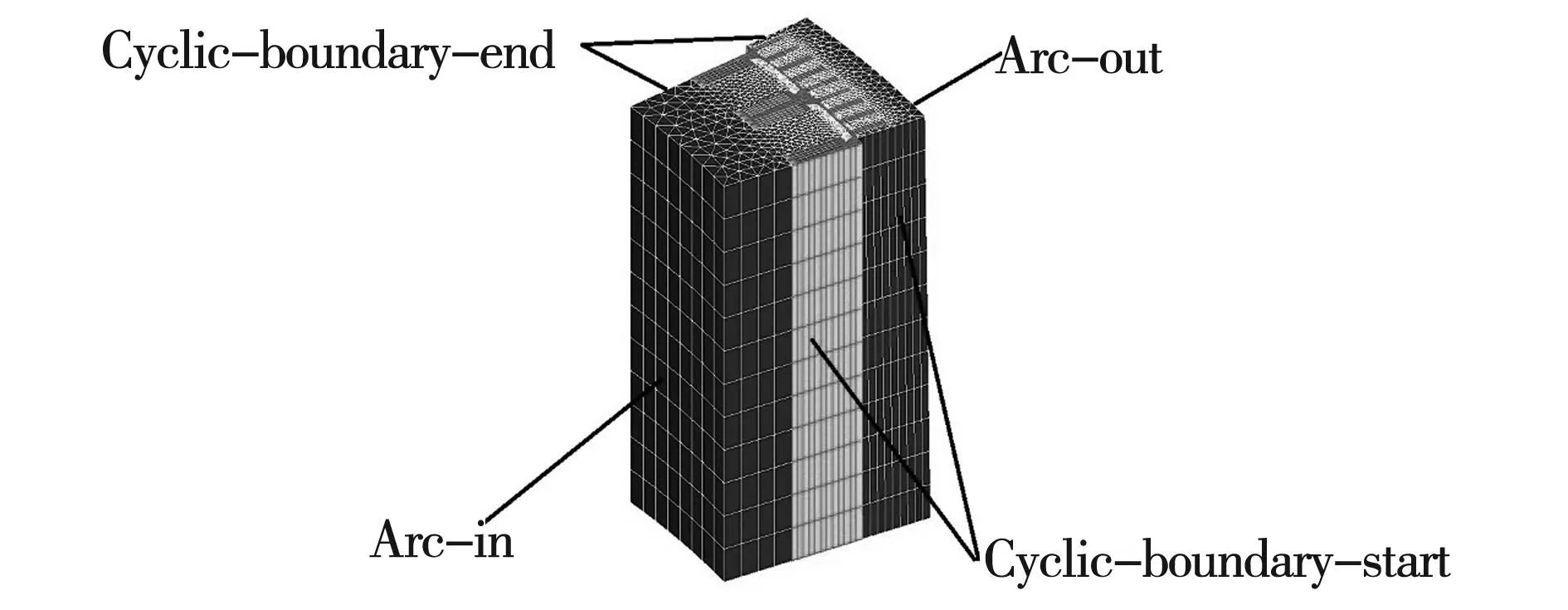
图1　电磁场求解区域与网格剖分Fig.1　Problem region and meshes of electromagnetic　　　 field

在求解区域内，考虑到铁心的饱和效应，描述非线性时变运动电磁场问题的偏微分方程为[21]

×(ν。

(1)

式中：A为矢量磁位；JS为外部强加的源电流密度；v为媒质的磁阻率；V为媒质相对于参考坐标系的运动速度；σ为媒质的电导率。

在三维多层运动电磁场模型中，对每一层而言，设电流密度和矢量磁位只有z轴分量，速度只有x轴分量。引入库仑规范▽·A=0，加入边界条件，便可得到发电机二维非线性时变运动电磁场的边值问题：

(2)

式中：Vx为速度的x轴分量；Jslz为源电流密度的z轴分量；Aslz为矢量磁位的z轴分量，它在转子磁轭内侧圆弧arc_in和定子磁轭外侧圆弧arc_out上满足第1类齐次边界条件，在电角度0度及360度的磁极分界线cyclic_ boundary_start和cyclic_boundary_end上满足整周期性边界条件。

1.3定转子电路模型

为了考虑定子绕组端部和转子阻尼绕组端环的影响，并能灵活设置运行工况，建立了相应的定转子电路模型[22]，把外电路方程和电磁场方程结合起来进行求解。

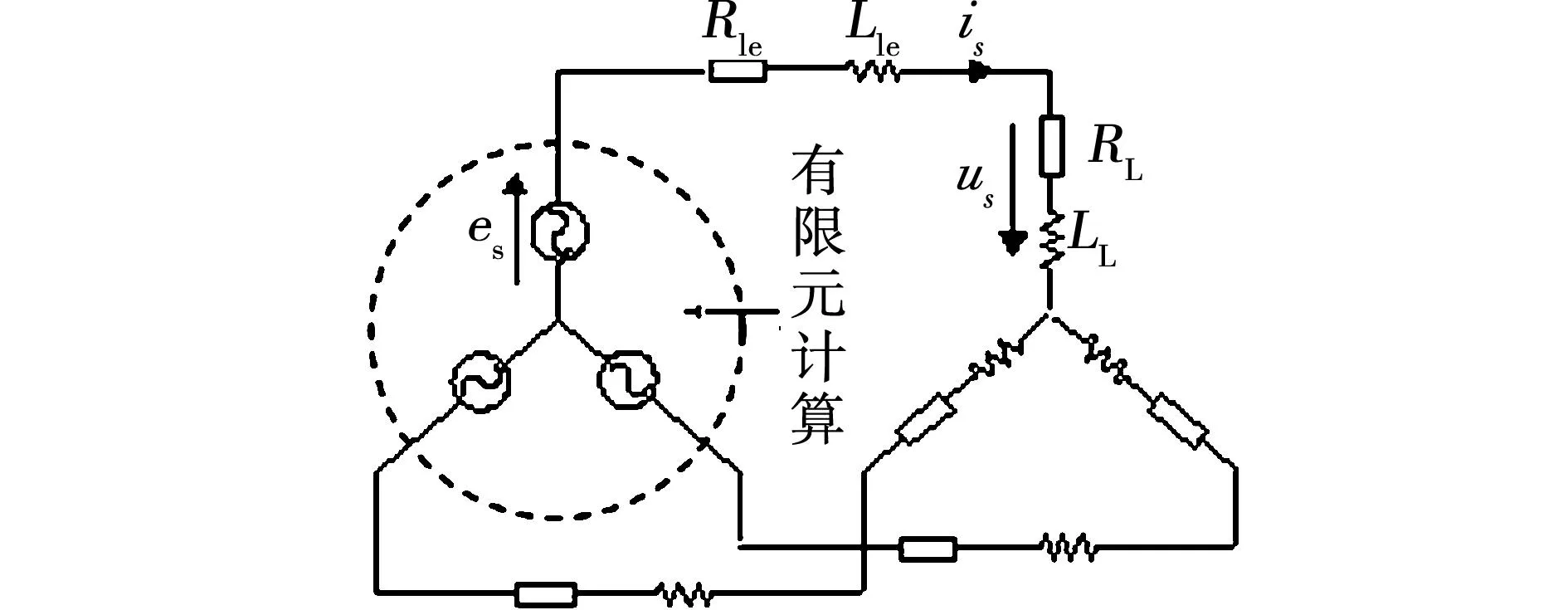
图2　定子负载电路Fig.2　Load circuit of the stator

根据如图2所示的定子绕组负载电路，可得到定子回路的电压方程式

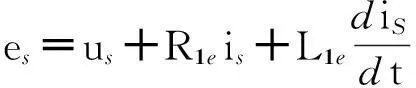
(3)

式中：es为定子相绕组直线部分感应电动势，通过有限元计算得到；us和is分别为定子绕组端电压和相电流；R1e和L1e分别为定子相绕组端部的电阻和漏电感。

而图中的RL和LL为发电机的负载电阻与负载电感，通过改变它们的设置值，能够设定发电机运行的不同工况。

根据图3所示的阻尼绕组电路结构，设iM、iM+1分别为第M根阻尼条左、右两侧的端环电流，它们与第M根阻尼条的电流iBM之间满足下列关系

iM+1-iM+iBM=0。

(4)

第M根和第M+1根阻尼条之间满足下列电压方程

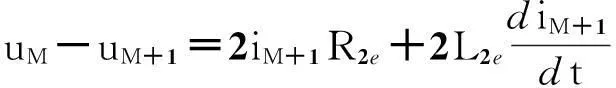
(5)

式中R2e和L2e分别阻尼绕组端环的电阻和电感。

设求解区域内有N根阻尼条，根据周期条件，可确定边界处电流和电压的约束条件为：

i1-iN+iB1=0，

(6)

(7)

将发电机定转子电路方程与电磁场边值问题方程联立，并设置负载电阻与电感，进行时间与空间离散，即可通过时步有限元计算，求出各层的矢量磁位Aslz，进而得出相应工况下的磁密、电压、电流以及损耗等计算结果。

图3　阻尼绕组电路Fig.3　Circuit of the damper winding

1.4发电机空载电压的计算

在图2中，设负载电阻RL及电感LL为无穷大，即可分析计算发电机的空载运行状态。通过时步有限元计算，即可求出空载线电压[21]

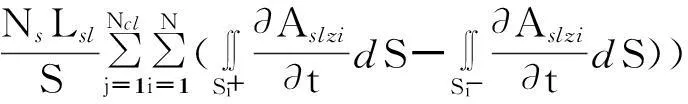
(8)

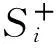
根据国家标准GB/T 1029-2005规定[23]，实际线电压波形与正弦波形的偏差程度一般用电压波形正弦性畸变率来表示,其值由下式确定

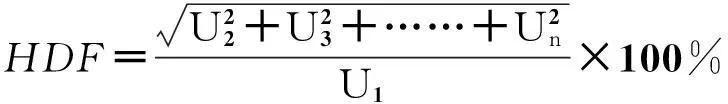
(9)

式中：U为线电压的有效值；Un为线电压中n次谐波的有效值。

对于大型发电机，国家标准规定，必须满足HDF≤5%。

1.5额定负载时阻尼绕组损耗的计算

在图2中，设负载电阻RL及电感LL为额定值，即可分析计算发电机的额定负载运行状态。

对于分层模型的第j层而言，第k根阻尼条的涡流密度为：

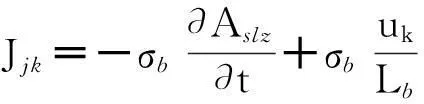
(10)

式中：σb为阻尼条电导率；Lb为阻尼条长度；uk为第k根阻尼条电压。

由此可得该阻尼条在第j层的1个剖分单元对应的电流和损耗分别为：

(11)

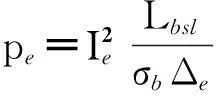
(12)

式中：Lbsl为阻尼条位于模型第j层的长度；Δe为该层阻尼条区域内1个剖分单元的面积

因此，整根阻尼条的涡流损耗可由下式计算

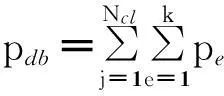
(13)

式中：k为单层内1根阻尼条区域的剖分单元总数；Ncl为模型分层数。

2转子三维温度场模型

2.1求解区域及其剖分

设发电机通风系统结构对称，转子温度分布关于其中心断面对称。这时，可把温度场的求解区域定为1个磁极从转子端面到中心断面的半个轴向段，该区域由转子铁心、阻尼绕组、励磁绕组、托板等部件组成，如图4所示。

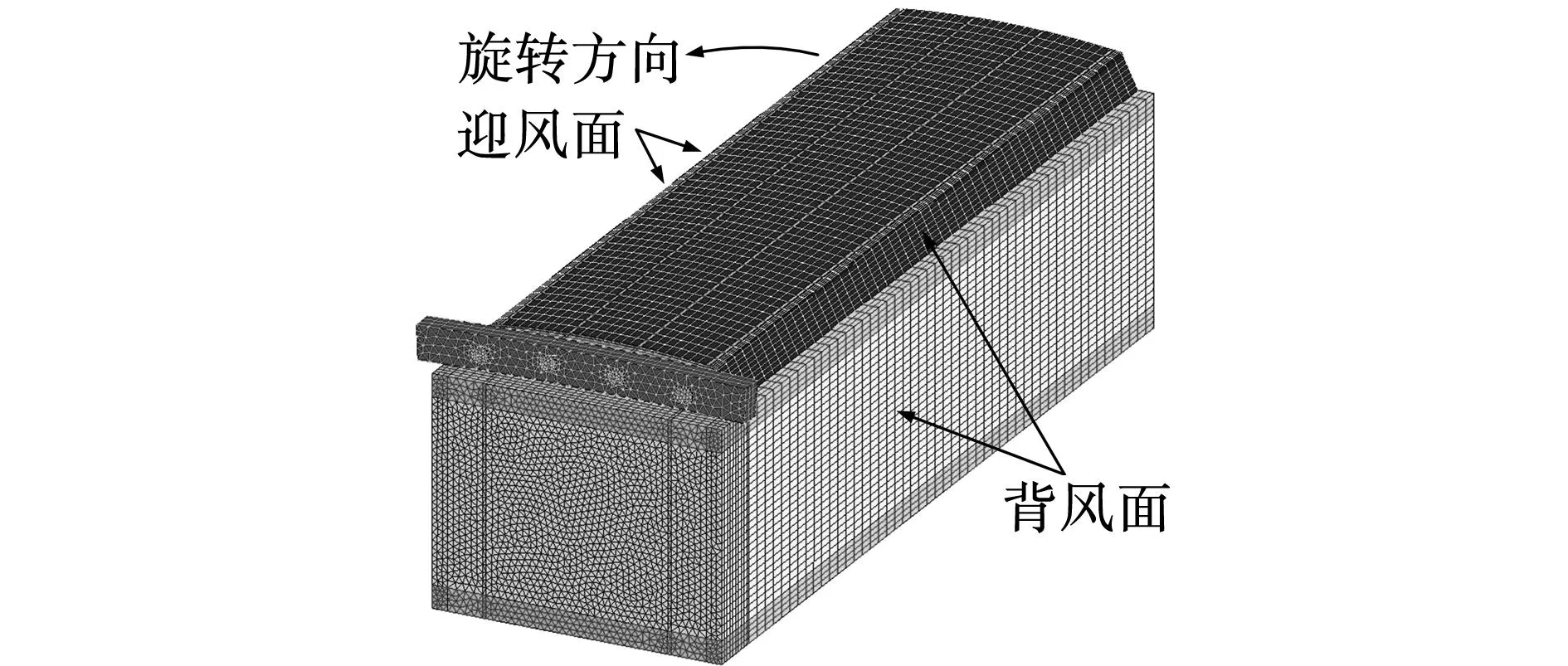
图4　温度场求解区域及网格剖分Fig.4　Problem region and meshes of temperature　　　 field

2.2转子三维温度场边值问题

考虑到转子磁极导热能力的各向异性特点，求解区域内的三维稳态温度场边值问题为：

(14)

式中：T为待求温度，℃；λx、λy、λz分别为x、y、z方向上的导热系数，W/(m·℃)；qv为热源密度，W/m3；S2为满足绝热边界条件的转子中心断面及转子与磁轭交界面；S3为满足散热边界条件的各边界面；α为S3边界面上的散热系数，W/(m2·℃)；Tf为S3边界面上的温度。

2.3散热系数的确定

转子旋转时，极靴上表面的散热系数和励磁绕组的散热系数分别为[24]：

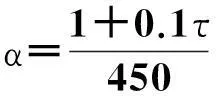
(15)

α″=Kα′。

(16)

式中：τ为极距，cm；K、α′根据电机结构确定。而考虑到转子迎风面的散热能力优于背风面，在确定其散热系数时，应分别乘以1个比例系数[25]。此处迎风面和背风面的比例系数分别取1.2和0.8，端面的散热系数取迎风面和背风面的平均值。

3计算结果与分析

3.1空载电压波形与谐波分析

针对所列的4类128种设计方案，进行时步有限元计算与空载电压分析。由于空载线电压Uab、Ubc、Uca对称，因此仅讨论Uab。部分计算结果如图5至图12所示。

由图5与图6可见，无论每极阻尼条根数nb=4还是nb=3，以下趋势都存在：

1)当定子未斜槽时，对于t2/t1而言，当其取值位于0.5～0.6与0.85～0.93区间时，HDF较大，波形质量较差，而当其取值位于0.75～0.85区间时，HDF较小，波形质量较好。

2)定子斜槽对HDF的抑制作用非较为明显，即使t2/t1取0.93这样HDF很大的方案，采取适当的斜槽措施后，其HDF仍然可以抑制到1%以下，从而获得较好的空载电压波形质量。

3)不同定子斜槽程度，对HDF的抑制效果不同，其中斜0.25槽、0.55槽与0.8槽方案对HDF抑制效果相对较差，而斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽方案对HDF的抑制效果较好，其中斜0.45槽与斜1槽的方案最好。

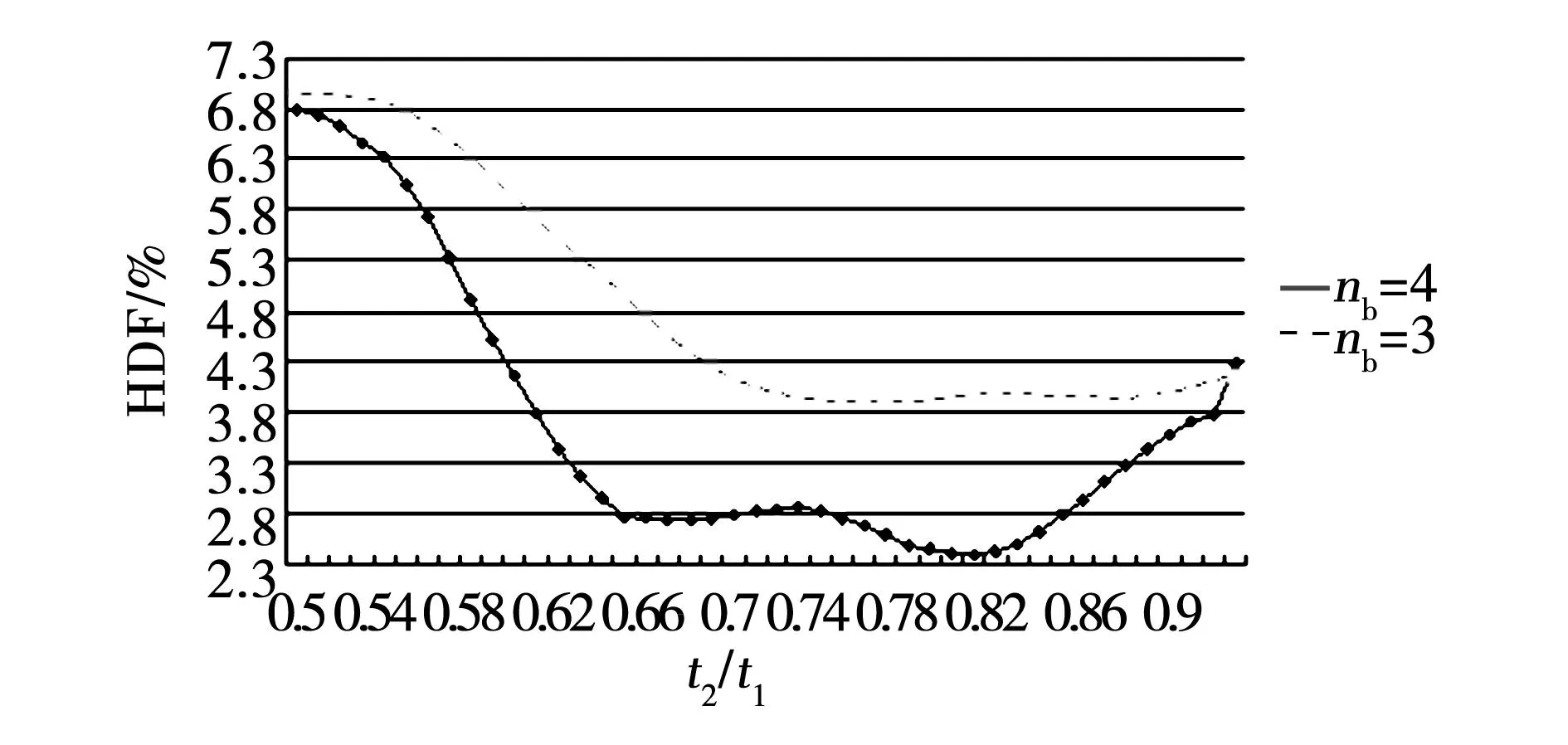
图5　HDF随t2/t1变化的曲线(nb=4,3,　　　定子无斜槽)Fig.5　HDF curve with different t2/t1　　　(nb=4,3,stator slot no skewed)

图6　HDF定子斜槽程度变化的曲线(nb=4,3,　　　 t2/t1=0.93)Fig.6　HDF curve with different stator slot skewing 　　　degree(nb=4,3,t2/t1=0.93)

4)对比图5中不同阻尼条根数nb所对应的HDF曲线可知，当仅采用调节t2/t1的方式优化空载电压波形时，较大nb的可能会更有效地抑制HDF，因此可能获得更好的空载电压波形。而由图6中不同阻尼条根数nb所对应的HDF曲线可见，对于nb=4与nb=3两种情况，其HDF随着斜槽程度增大而变化的曲线形状相似，但较大的nb仍然有助于抑制HDF。

为进一步探讨造成上述结果的原因，对空载电压进行谐波分析。在进行谐波分析时，应注意考虑齿谐波的影响。这类谐波在频谱中次数为

ν=k2mq±1。

(17)

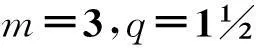
除此之外，还应注意分析其余高次谐波分量的影响。

对部分方案进行谐波分析后，所得空载电压谐波分布情况如图7与图8所示。

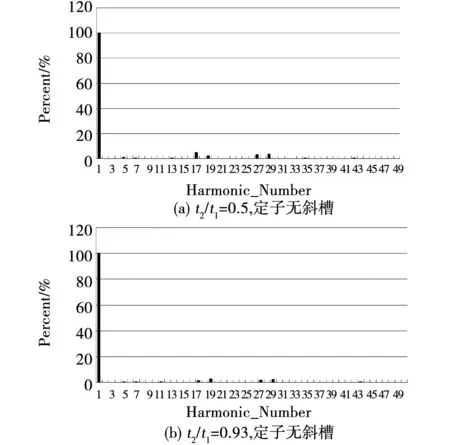
图8　空载电压谐波分布(nb=3)Fig.8　Voltage harmonics distribution at no-load 　　　(nb=3)

由图7与图8可见，对空载电压波形影响较大的谐波，除了属于2阶齿谐波的17次和19次谐波之外，还有27次和29次谐波。

随后对所有设计方案的一阶与二阶齿谐波及27次和29次谐波的分布及变化情况进行分析，得出一阶与二阶齿谐波及27次和29次谐波随t2/t1及定子斜槽程度变化的趋势如图9与图10所示。

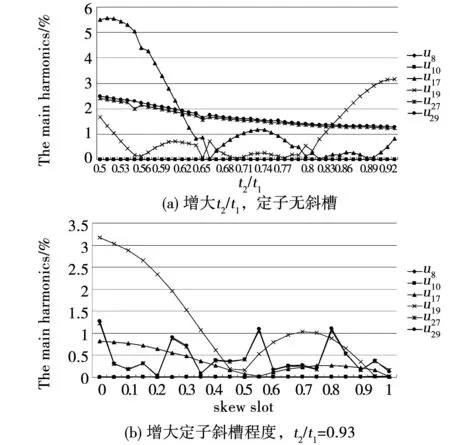
图9　空载电压主要谐波随t2/t1及　　　定子斜槽程度变化规律(nb=4)Fig.9　Main voltage harmonics variation at　　　no-load (nb=4)

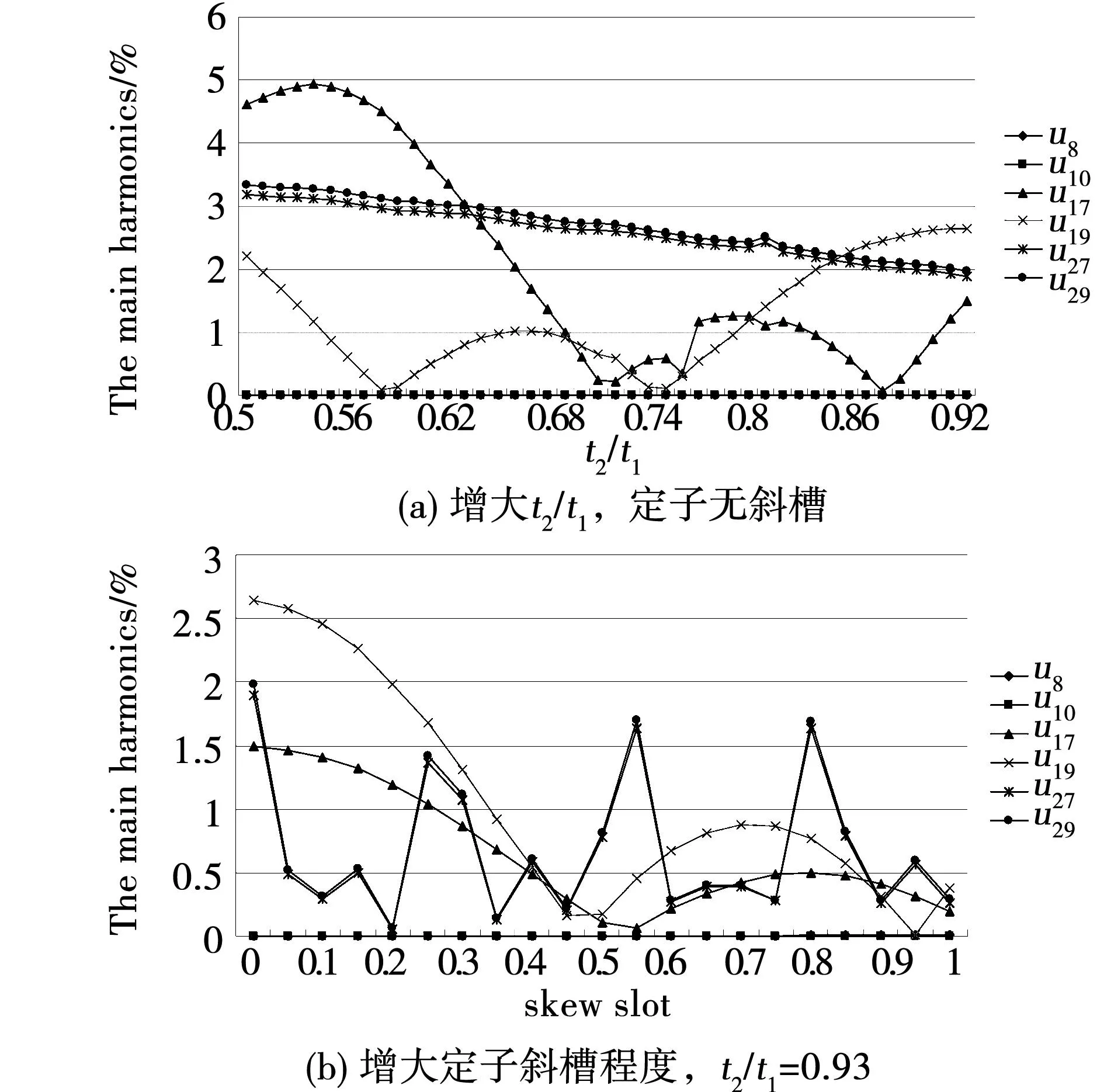
图10　空载电压主要谐波随t2/t1及　　　定子斜槽程度变化规律(nb=3)Fig.10　Main voltage harmonics variation at 　　　no-load (nb=3)

由图9与图10可见，无论每极阻尼条根数nb=4还是nb=3，在本次研究的t2/t1与定子斜槽程度变化区间内，一阶齿谐波(8次与10次)的影响都可以忽略，而二阶齿谐波(17次与10次)及27次和29次谐波较为明显。

因此，为进一步分析二阶齿谐波和27次与29次谐波对HDF的影响，设参数Fu如式(18)所示。

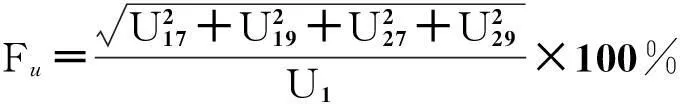
(18)

随后得出Fu随t2/t1及定子斜槽程度变化的情况，如图11与图12所示。

图11　主要谐波对空载电压HDF的影响(nb=4,3,　　　增大 t2/t1，定子无斜槽)Fig.11　Influence of main voltage harmonics on HDF　　　at no-load (nb=4,3,stator slot no skewed)

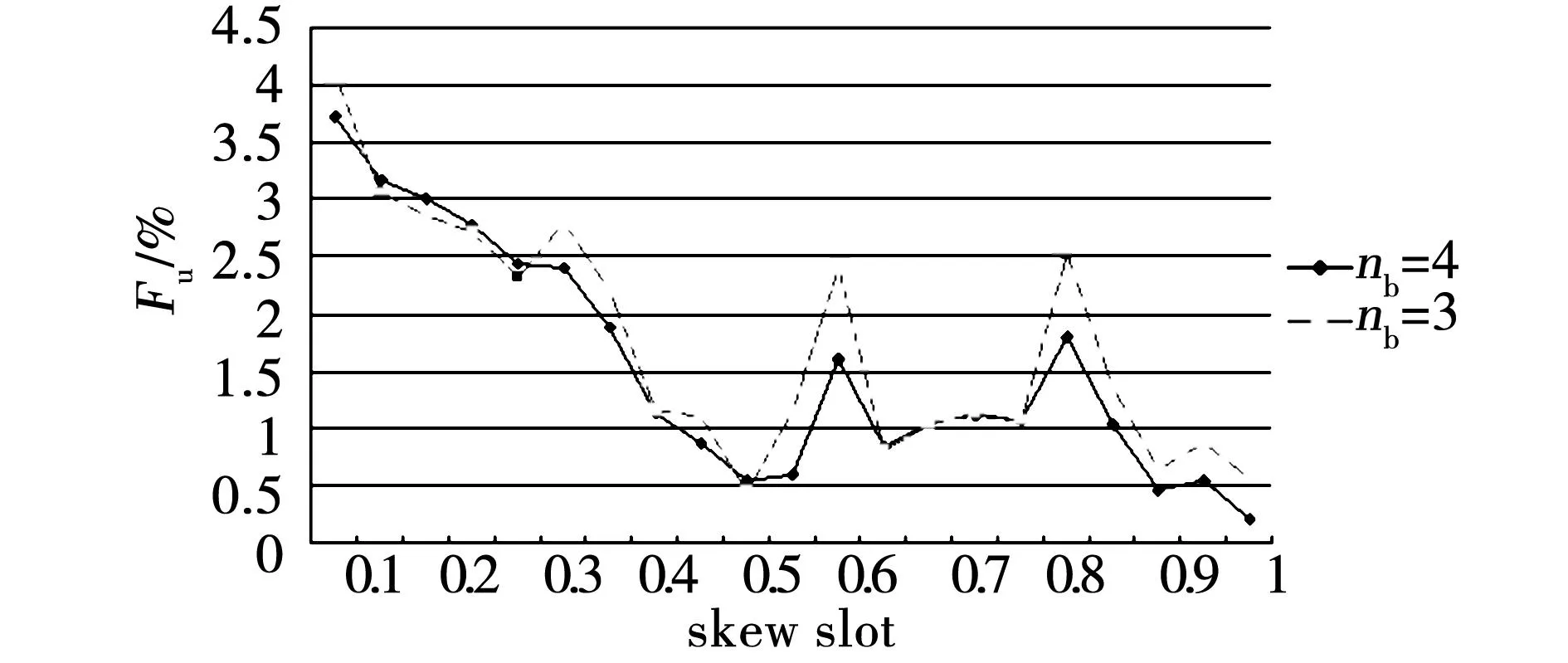
图12　主要谐波对空载电压HDF的影响(nb=4,3,　　　 t2/t1=0.93，定子斜槽)Fig.12　Influence of main voltage harmonics on HDF　　　 at no-load (nb=4,3,t2/t1=0.93，stator slot　　　 skewed)

由图9与图12可知：

2)当定子不斜槽时，随着t2/t1的增大，27次与29次谐波持续减小，但在t2/t1的某些取值区域，二阶齿谐波(17次与19次)仍然较为明显，因此HDF较大，空载电压波形质量较差，如t2/t1取值位于0.5～0.6与0.85～0.93区间的情况。只有当t2/t1取值位于上述两类谐波都较小的区域时，HDF较小，空载电压波形质量较好，如t2/t1取值位于0.75～0.85区间的情况。

3)采用调整定子斜槽的措施抑制HDF时，对二阶齿谐波(17次与19次)的削弱较为明显，但某些斜槽方案仍然存在较为明显的27次与29次谐波，因此其HDF较大，空载电压波形质量较差，如斜0.25槽、斜0.55槽及斜0.8槽的情况。只有上述两类谐波都较小的方案，才会有较小的HDF与较好的空载电压波形质量，如斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽方案。

4)对比上述HDF较小的斜槽方案可以发现，其HDF较为接近，特别是效果最好的斜0.45槽方案与斜1槽方案，其HDF几乎相同。如表3所示。这就意味着采用较小的斜槽程度，如斜0.45槽或斜0.5槽，可以获得接近于斜1槽的优质波形。

表3　不同定子斜槽程度对应的HDF

3.2阻尼条损耗发热分析

发电机额定负载工况下，阻尼条损耗发热计算结果如图13到图16所示，其中，∑P为一个磁极上的阻尼绕组总损耗，Tmax表示阻尼绕组最高温度。

由此可知，无论每极阻尼条根数nb=4还是nb=3，以下趋势都存在：

1)采用调整t2/t1的措施，对阻尼条损耗发热的影响较为明显，其中，当t2/t1的取值位于0.85～0.93区间时，阻尼条损耗发热较小。

2)采用定子斜槽措施，对阻尼条损耗发热具有一定的抑制作用，但效果远不如调整t2/t1。

3)如果仅采用调整t2/t1的措施来抑制阻尼条损耗发热，当t2/t1取值位于某些区间时，阻条损耗发热较小，但空载电压HDF较大，空载电压波形质量较差，如t2/t1的取值位于0.85～0.93的情况；而当t2/t1取值位于另一些区间时，空载电压HDF较小，空载电压波形质量较好，但阻尼绕组损耗发热相对较大，如t2/t1取值位于0.75～0.85与区间的情况。

图13　额定负载工况下阻尼绕组总损耗随t2/t1变化曲线　　　(nb=4,3,增大t2/t1，定子无斜槽)Fig.13　Losses of damper bars of the different t2/t1　　　at rated-load　　　(nb=4,3,stator slot no skewed)

图14　额定负载工况下阻尼绕组总损耗随斜槽程度变化　　　曲线(nb=4,3,t2/t1=0.93，定子斜槽)Fig.14　Losses of damper bars of the different　　　stator slot skewing degree at rated-load　　　(nb=4,3,t2/t1=0.93，stator slot skewed)

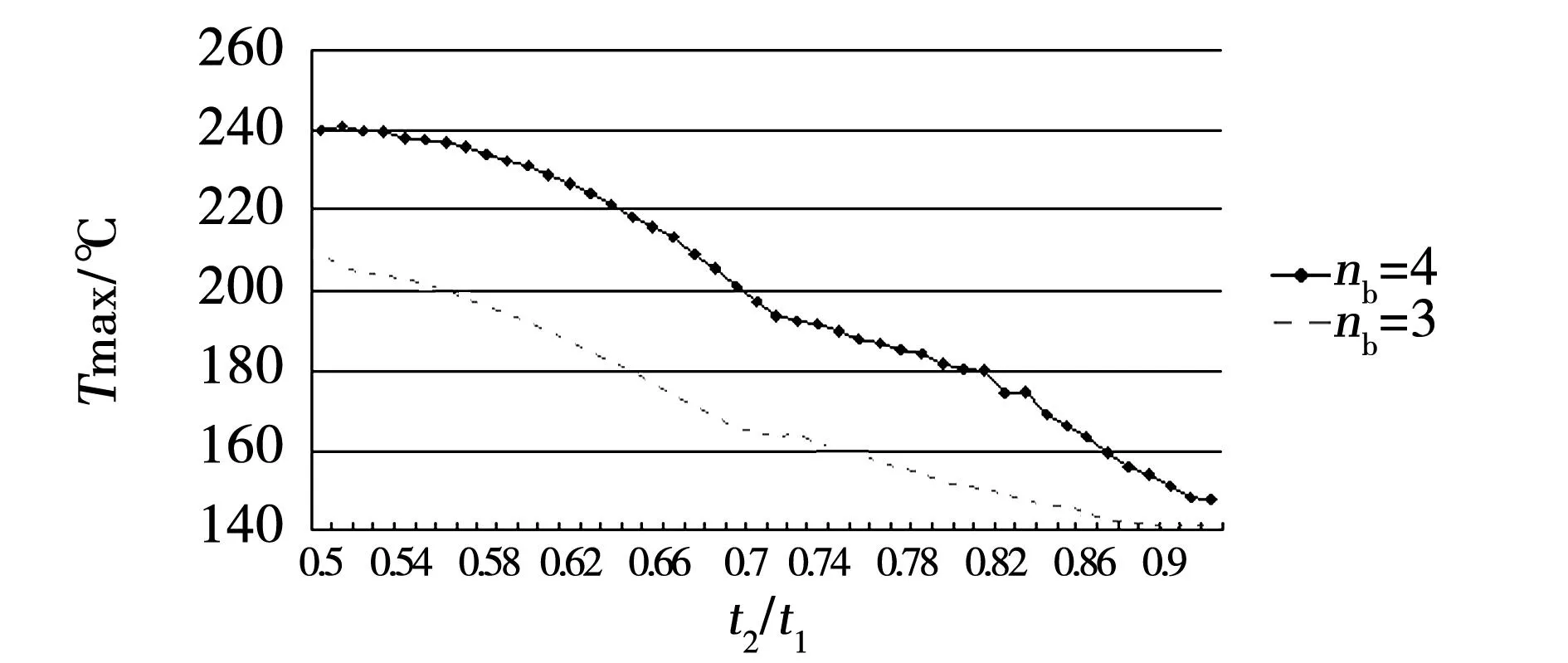
图15　额定负载工况下阻尼绕组最高温度随t2/t1变化　　　曲线(nb=4,3,定子无斜槽)Fig.15　Tmax of the different t2/t1 at rated-load　　　(nb=4,3,stator slot no skewed)

4)针对t2/t1的取值位于0.85～0.93区间的设计方案，采取斜槽措施，既可以获得较低的HDF与较好的空载电压波形，又可以获得较低阻尼绕组损耗发热。即使是波形质量较差的t2/t1=0.93的方案，在采用斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽等方案后，也能获得较好的空载电压波形与较低的阻尼绕组发热。且对比上述几种斜槽方案可知，其阻尼条最高温度Tmax十分接近，这就意味着，采用较小的斜槽程度，如斜0.45槽或斜0.5槽，可以获得接近于斜1槽的较低的损耗和发热，如表4所示。

图16　额定负载工况下阻尼绕组最高温度随斜槽　　　程度变化曲线　　　(nb=4,3,t2/t1=0.93，定子斜槽)Fig.16　Tmax of the different stator slot skewing　　　 degree at rated-load　　　(nb=4,3,t2/t1=0.93，stator slot skewed)

5)对比不同的阻尼条根数nb所对应的Tmax可知，无论是采用调整t2/t1的措施，还是采用斜槽措施，当阻尼条根数nb较少时，阻尼条的损耗发热相对较低。

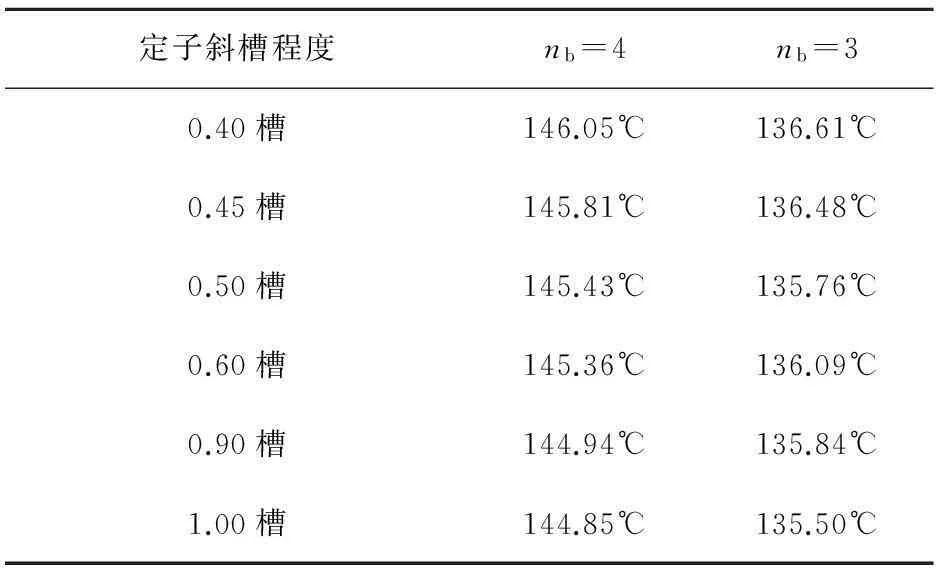
表4　不同的定子斜槽程度对应的阻尼条最高温度

3.3空载波形计算结果验证

为了验证计算的准确性，针对算例机组真机实际采用的方案(nb=4，t2/t1=0.93，定子斜0.5槽)，进行了空载电压测量。

试验所需仪表如表5所示。

测量中时间采样频率设置为0.01 ms，并对空载电压波形进行傅里叶分析，谐波频率分析到5 000 Hz。对发电机空载相电压和线电压分别进行了测量。测量接线图与结果界面见图17与图18。

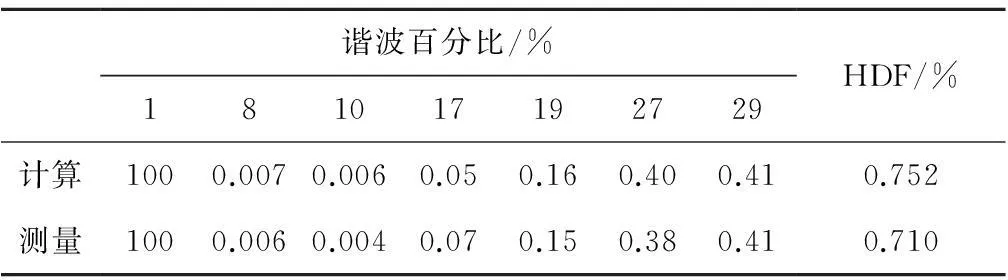
空载线电压波形测量结果数据如表6所示。

由对比可见，对空载电压波形的计算分析结果与测量值较为吻合，准确性较高。

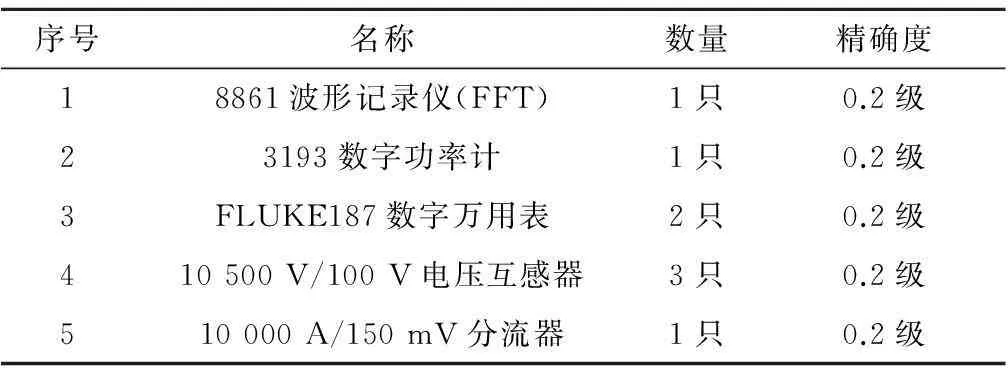
表5　试验所需仪表

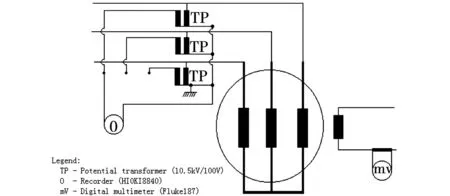
图17　电压波形测量接线图Fig.17　Schematics of voltage waveforms test

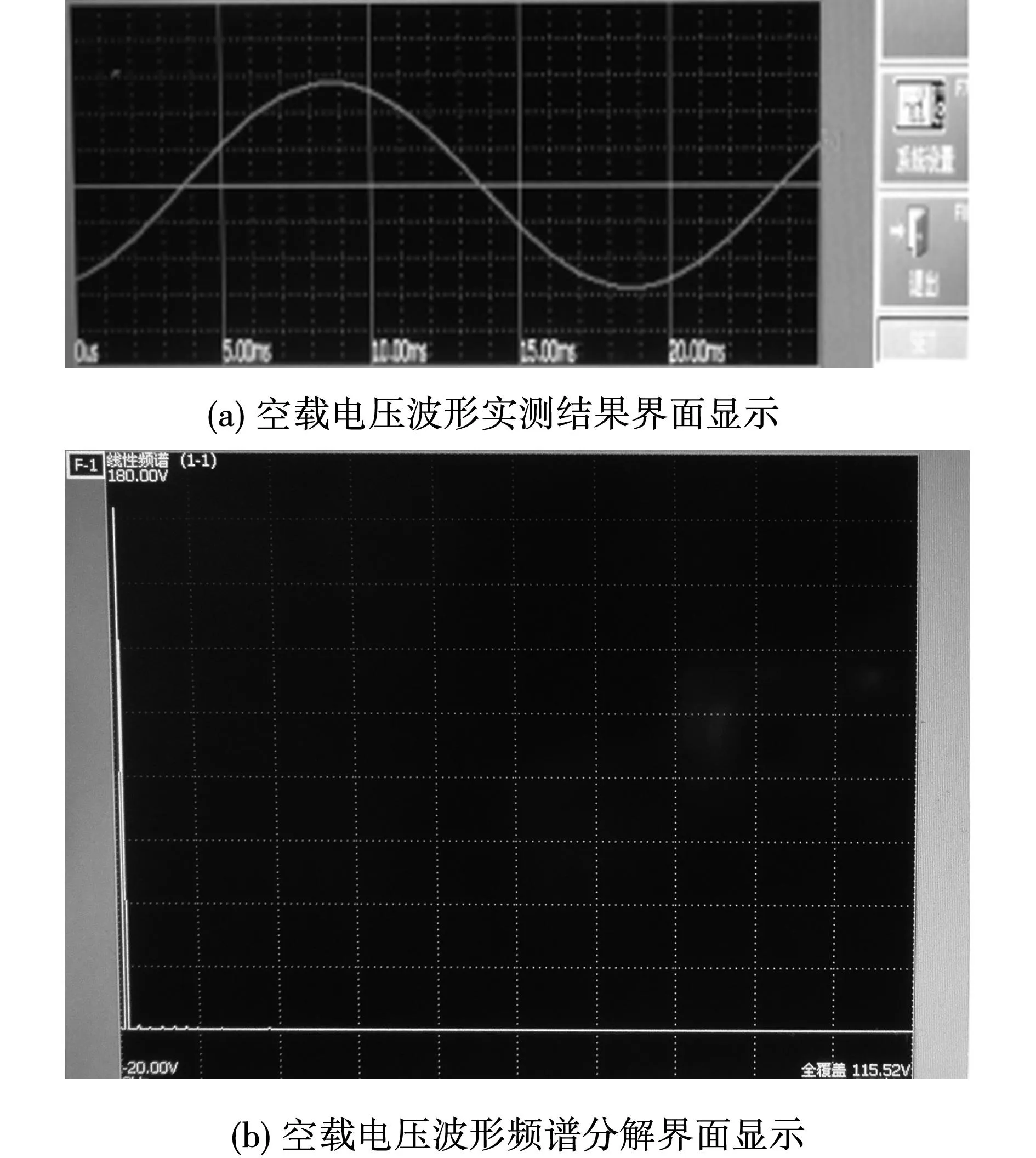
图18　电压波形测量现场照片Fig.18　Photograph of voltage waveforms test scene

谐波百分比/%181017192729HDF/%计算1000.0070.0060.050.160.400.410.752测量1000.0060.0040.070.150.380.410.710

4结论

无论是单纯增大阻尼绕组节距t2，还是单纯调节定子斜槽程度，或是单纯改变每极阻尼条根数，都难以全面保证对空载电压波形畸变率和阻尼绕组损耗发热的抑制效果。

只有在合理增大nb与t2的同时，采用合理的斜槽措施，如斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽等方案，才有可能同时获得较好的空载电压波形和较低的条损耗发热。如本文机组实际采用的nb=4，t2/t1=0.93，定子斜0.5槽方案，就是一种较为满意的方案。

本文的计算模型，能够较为精确地预测各种结构设计方案对水轮发电机空载电压波形与阻尼绕组发热的影响，从而能够为水轮发电机设计制造、发电机与电网的运行保护，提供更为有益的参考。

参 考 文 献:

[1]李朝阳．贯流式机组在低水头电站的应用[J]．发展，2006，19(9)：145-146．

LI Chaoyang．The application of bulb-type hydro-generator set at low head hydropower station[J]．Developing,2006,19(9): 145-146．

[2]邓东，孙玉田，谭国伟，等．飞来峡水电站发电机的运行故障分析[J]．大电机技术，2003，33(6)：13-17．

DENG Dong,SUN Yutian,TAN Guowei,et al．Analysis on operating faults of generator in Feilaixia hydropower station[J]．Large Electric Machine,2003,33(6): 13-17．

[3]李哲生.凸极同步电机的空载气隙磁场(Ⅰ)[J]．哈尔滨电工学院学报，1982，5(3)：16-31.

[4]李哲生.凸极同步电机的空载气隙磁场(Ⅱ)[J]． 哈尔滨电工学院学报，1982，5(4)：1-10.

[5]李哲生.凸极同步电机的谐波电势(Ⅰ)[J]．哈尔滨电工学院学报，1983，6(1)：1-10.

[6]李哲生.凸极同步电机的谐波电势(Ⅱ)—阻尼绕组的影响[J]． 哈尔滨电工学院学报，1983，6(2)：1-18.

[7]李哲生.改善凸极同步发电机空载电势波形的措施[J]．哈尔滨电工学院学报，1983，6(3)：1-16.

[8]CHANGEOBKIM,SYKULSKI JK．Harmonic analysis of output voltage in synchronous generator using finite element method taking account of the movement[J]．IEEE Trans on Magnetics,2002,38(2):1249-1252．

[9]李槐树，李朗如，让余奇．阻尼绕组对凸极同步发电机空载电势波形的影响[J]．电机与控制学报，2003，7(4)：267-271．

LI Huaishu,LI Langru,RANG Yuqi．The effect of damper winding on the no-loadvoltage waveform of salient-pole synchronous generator[J]．Electric Machines and Control,2003,7(4): 267-271．

[10]KELLER S,XUAN M T,SIMOND J J．Computation of the no-Load voltage waveform of laminated salient-pole synchronous generators[J]．IEEE Trans.on Industry Applications,2006,42(3):681-687．

[11]WANG Shanming,WANG Xiangheng,LI Yixiang et al．Steady-state performance of synchronous generators with ac and dc stator connections considering saturation[J]．IEEE Trans.on Energy Conversion,2002,17(2):176-182．

[12]周光厚，韩力，范镇南，等 采用不对称磁极优化水轮发电机空载电压波形[J].中国电机工程学报，2009，29(15)：67-73．

ZHOU Guanghou,HAN Li,FAN Zhennan,et al.No-load voltage waveform optimization of hydro-generator with asymmetric poles[J]．Proceedings of the CSEE,2009，29(15)：67-73．

[13]GEORG T S,SHOMAS L,ALEXANDER S.Add loss in thedamper winding of large hydrogenerator at open-circuit and load conditions[J]．IEEE Transactions on Industrial Electronics,2010，57(1)：154-160．

[14]TANZO N,TAKAO O,TADASHI N,et al.Analysis of damper winding current of synchronous generator due to space subharmonic M.M.F[J]．IEEE Transactions on Magnetics,1983，19(6)：2643-2646．

[15]KELLER S,XUAN M T,SIMOND J J,et al.Large low-speed hydro-generator-unbalanced magnetic pulls and additional damper losses in eccentricity conditions[J]．IET Electr.Power Appl,2007，21(5)：657-664．

[16]郭景斌、周爱清、徐跃云.进口灯泡水轮发电机阻尼绕组和磁极损坏机理分析[J]．中国电力，2001，34(5)：13-16．

GUO jingbin,ZHOU Aiqing,XU Yueyun.Analysis of damaged damping winding and magnetic pole in the type generator[J]．Electric China,2001，34(5)：13-16．

[17]李伟力，周封，侯云鹏，等．大型水轮发电机转子温度场的有限元计算及相关因素的分析[J].中国电机工程学报，2002，22(10)：85-90．

LI Weili,ZHOU Feng,HOU Yunpeng,et al．Calculation of rotor temperature field for hydro-generator as well as the analysis on relevant factors[J]．Proceedings of the CSEE,2002,22(10): 85-90．

[18]李伟力，陈玉红，霍菲阳，等.大型水轮发电机转子旋转状态下磁极间流体流动与温度场分析[J]． 中国电机工程学报，2013，32(9)：132-140.

LI Weili,CHEN Yuhong,HUO Feiyang,et al.Fluid flow and temperature field analysis between two poles of a large air-cooled hydro-generator rotor in rotation[J]．Proceedings of the CSEE，2013，32(9)：132-140.

[19]范镇南，韩力，周光厚，等.大型贯流式水轮发电机阻尼绕组损耗与发热[J].高电压技术，2011，37(2)：468-475.

FAN Zhennan， HAN Li,ZHOU Guanghou,et al.Losses and heat on damper winding in large tubular hydro-generator[J].High Volt age Engineering,2011，37(2)：468-475.

[20]范镇南，廖勇，谢李丹，等.贯流式水轮发电机空载电压波形优化与阻尼条发热抑制[J].高电压技术，2012，38(5)：1233-1242.

FAN Zhennan，LIAO Yong,XIE Lidan,et al.No-load voltage waveform optimization and damper bars heat reduction of tubular hydro-generator[J].High Volt age Engineering,2012，38(5)：1233-1242.

[21]胡敏强，黄学良等．电机运行性能数值计算方法及应用[M]．南京：东南大学出版社，2003．

[22]PIRIOU F，RAZEK A．Finite element analysis in electromagnetic systemsaccounting for electric circuits[J]．IEEE Trans.on Magnetics，l993，29(2)：1669-1675．

[23]富立新等．GB/T 1029-2005．三相同步电机试验方法[S]．北京：中国标准出版社，2006．

[24]白延年．水轮发电机设计与计算[M]．北京：机械工业出版社，1982．

[25]魏永田，孟大伟，温嘉斌,等．电机内热交换[M]．北京：机械工业出版社，1998．

(编辑：贾志超)

Reduction of no-load voltage waveform distortion and damper bar heat of tubular hydro-generator

FAN Zhen-nan1,2,HAN Li2,LIAO Yong2,DONG Xiu-cheng1，WANG Jun1

(1.School of Electrical engineering and Electronic Information,Xihua University,Chengdu 610039,China;2.State Key Laboratory of Power Transmission Equipment & System security and New Technology,Chongqing University，Chongqing 400030,China)

Abstract:To improve the power quality of hydro-generator,prevent the overheat of damper bar and ensure the safe operation of the generator unit and the grid,the electromagnetic field theory,the circuit theory and heat transfer theory are used to establish a 3D multi-slice moving electromagnetic field-circuit coupling model of hydro-generator and a 3D temperature field model of the rotor pole.Then the models are used to calculate 128 structure design schemes of a 36 MW fractional slot tubular (q=1),and the influence of the variation of damper bar pitch,stator slot skewing degree and number of damper bars per pole on the no-load voltage distortion and damper bar loss and heat are analyzed.Furthermore,the optimized measures are presented and the calculation results are coincident well with the test data.

Keywords:tubular hydro-generator,no-load voltage distortion,loss and heat of damper bar,electromagnetic field,temperature field

中图分类号:TM 312

文献标志码:A

文章编号:1007-449X(2016)04-0017-10

DOI:10.15938/j.emc.2016.04.003

通讯作者:范镇南

作者简介：范镇南(1981—)，男，博士，讲师，研究方向为电机与电力设备物理场分析与状态评估；

基金项目：中央高校基本科研业务费资助(CDJXS11151152)；四川省教育厅重点科研项目(16ZA0155)；西华大学重点科研基金资助项目(Z1520907)

收稿日期:2014-07-04

韩力(1963—)，男，博士，教授，研究方向为电机与电力设备物理场分析与状态评估，电机优化设计；

廖勇(1964—)，男，博士，教授，研究方向为电机的分析与控制；

董秀成(1963—)，男，硕士，教授，研究方向为电气控制与信息处理；

王军(1966—)，女，博士，教授，研究方向为电机的分析与控制。