单相PWM整流器定频模型预测功率控制算法
2016-05-16宋文胜邓知先
宋文胜, 邓知先
(西南交通大学 电气工程学院,四川 成都 610031)
单相PWM整流器定频模型预测功率控制算法
宋文胜,邓知先
(西南交通大学 电气工程学院,四川 成都 610031)
摘要:针对传统单相PWM整流器开关表直接功率控制算法的系统功率脉动大、开关频率不固定、网侧谐波高等问题,借鉴三相PWM整流器的模型预测直接功率控制(MP-DPC)算法,提出了一种基于占空比优化的单相PWM整流器MP-DPC算法。首先,依据瞬时功率理论,通过虚拟坐标系构造网侧电压与电流的旋转矢量,给出了一种单相系统功率求解算法;然后,研究不同开关状态对系统功率的影响,给出了单相PWM整流器最优开关状态选择与占空比求解的MP-DPC方法;最后,分别对滞环开关表DPC与MP-DPC算法进行了计算机仿真及半实物实验对比研究,结果表明:与滞环开关表DPC算法相比,该MP-DPC算法具有控制精度高、开关频率恒定、网侧电流谐波含量低等优点,也验证了该算法的有效性和优越性。
关键词:单相PWM整流器; 直接功率控制; 模型预测控制; 占空比优化; 半实物实验
0引言
近年来,随着电力电子器件制造技术、微电子技术和控制技术的不断发展与革新,电力电子变流器的性能得到了不断提高。目前,高性能的交-直-交变流器已经在轨道交通列车牵引传动系统、风力发电等重要领域广泛应用[1-3]。对于交-直-交变流器中PWM整流器来说,其控制目标都是维持直流侧电压恒定、减小网侧电流谐波含量、提高功率因数和加快系统动态响应速度[1,4]。目前其广泛采用的控制算法是直接电流控制(direct current control,DCC),主要包括滞环直接电流控制、瞬态电流控制、预测电流控制、dq坐标系直接电流控制等[4]。
与直接电流控制算法相比,直接功率控制(direct power control,DPC)是以系统瞬时功率为控制对象,由于其较高的控制精度和响应速度,国内外学者对三相PWM变流器的直接功率控制方法开展了大量的研究[2-9]。例如:滞环开关表DPC算法实现简单、系统响应速度快,但所选开关矢量只能偏向有功或无功进行控制,文献[5]中采用增加扇区数量、细化开关表DPC算法和文献[6]中采用双开关表DPC算法都可以达到减少系统功率波动;文献[7]对三相交-直-交变流系统的开关表滞环DPC算法与传统DCC算法进行了比较,DPC算法具有动态性能好、控制策略简单、系统容易实现等优点;文献[8]提出了一种准定频控制策略,降低了开关频率和采样频率。文献[10-11]将预测控制应用于直接功率控制,提高了系统响应速度,实现了输出功率快速跟踪。文献[12]提出了一种三相变流器系统MP-DPC算法,不但降低网侧谐波,提高动态性能的同时,且对系统有功与无功功率都实现了精确控制。文献[13-14]在文献[12]提出MP-DPC基础上进行了矢量占空比优化,进一步减小了系统功率的脉动。
目前,国内外对其单相直接功率控制算法的研究相对较少。文献[15-16]中提出了几种单相电路功率检测方法,文献[1]和文献[17-19]中分别介绍了单相变流器的滞环开关表、功率预测的功率内环控制算法。由于滞环开关表开关频率不固定、功率预测算法复杂等缺点,直接功率控制算法在单相变流器的应用仍有待深入研究。
本文首先建立了单相PWM整流器的数学模型,详细地分析了单相直接功率控制的基本原理,提出了一种基于占空比优化的单相PWM整流器MP-DPC算法。该算法首先计算各有效矢量的最优占空比,再根据评价函数选择最佳矢量及其相应的最优占空比,不但将三相系统的MP-DPC算法引入了到了单相系统中,也对该算法的性能进行了改进和提升。最后,对该MP-DPC算法和滞环开关表DPC算法进行了计算机仿真和半实物实验的对比研究。
1单相PWM整流器数学模型
单相PWM整流器基本拓扑结构如图1所示,基本电压方程可以表示为

(1)
式中:us、is为网侧电压、电流;L为网侧电感;R为网侧电源及线路阻抗;uab为整流桥的输入端电压。
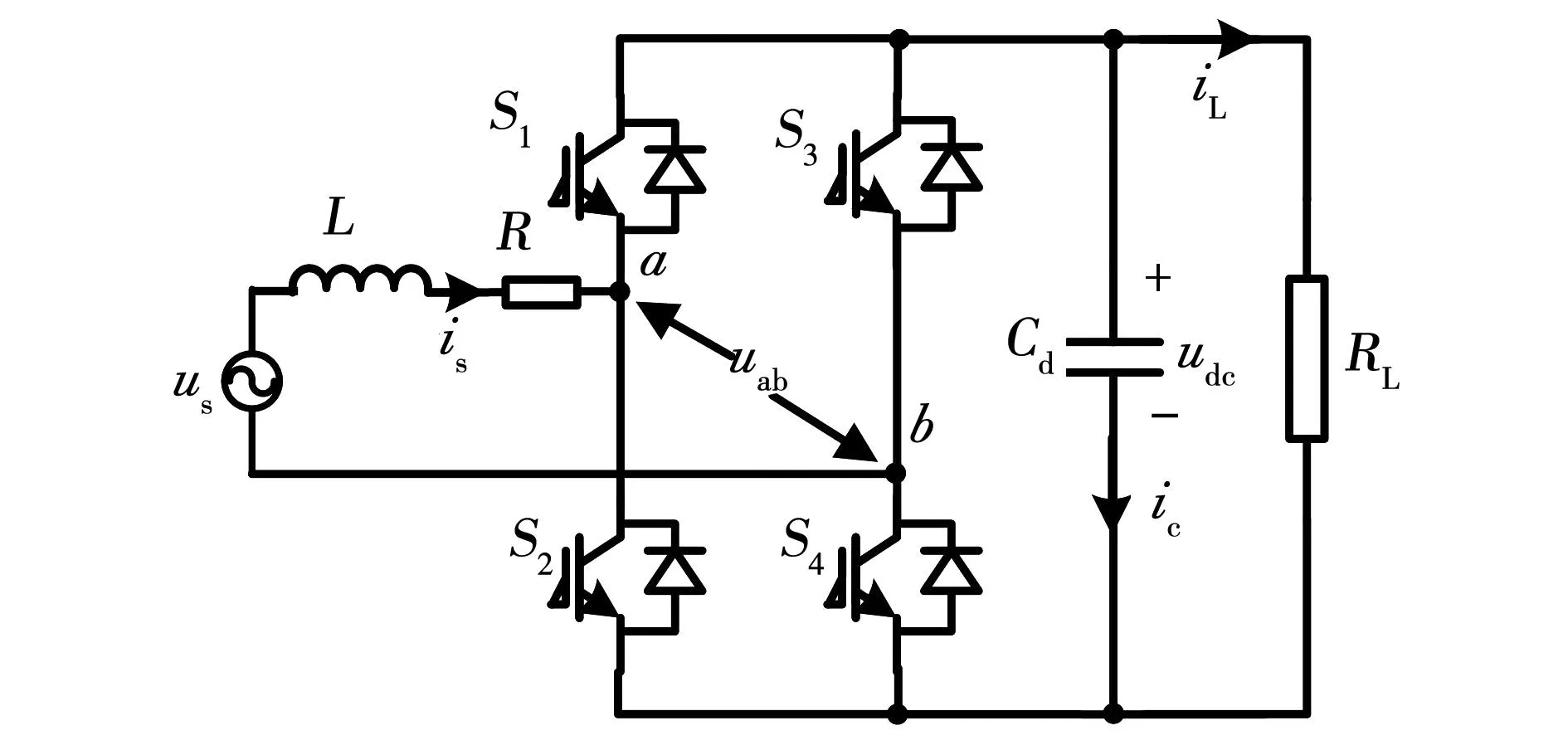
图1 单相PWM整流器拓扑Fig.1 Topology of a single-phase PWM rectifier
式(1)在构造的静止坐标系及旋转坐标系中仍然适用,其中R较小,可以忽略。整理后即可得
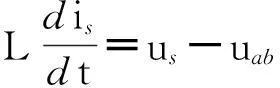
(2)
由于单相系统仅能获得网侧电压、电流的标量值,而无法构成旋转电压、电流矢量,则无法得到相应的有功功率和无功功率。因此,必须构造一个滞后于网侧电压与电流90°的虚拟电压与电流,两者叠加后获得网侧电压与电流旋转矢量用以求出系统功率。
依据瞬时功率理论,视在功率可以定义为

(3)
将合成旋转电压、电流矢量进行αβ分解
(4)
式中:uα、iα为实测网侧电压和电流值,也即电压矢量us和电流矢量is在两相静止αβ坐标系下的α轴分量;uβ、iβ为实测网侧电压和电流延迟90°值,也即电压矢量us和电流矢量is在两相静止αβ坐标系下的β轴分量。
将式(4)代入式(3),则单相系统的瞬时有功功率与无功功率可表示为
(5)
式(5)中变量都为静止αβ坐标系下标量,可以合成网侧电压、电流的旋转矢量,同时可以精确计算出系统功率的瞬时值。
开关函数是开关状态的一种表示方法,在单相PWM整流器中,每个桥臂中的两个开关状态Sx(x=1,2,3,4)始终互补,S1/S3导通、S2/S4关断与S1/S3关断、S2/S4导通效果相同,开关函数可定义并简化为
(6)
对于单相两电平整流器,可以用开关函数Sab与直流侧电压表示整流器网侧输入端电压为
(7)
式中,udc为直流侧电容电压。
2模型预测直接功率控制
MP-DPC算法是在每个开关周期内根据被控对象(整流器)的数学模型以及当前时刻的采样值,计算整流器此控制周期内所选取开关状态的作用时间或开关状态组合的占空比大小,使系统有功与无功功率能够快速地跟踪设定值,具有动态响应迅速,计算简易等优点,同时能够兼顾多个目标参数。但模型预测直接功率控制依赖于系统的数学模型,系统电路参数越精确,控制性能越好。
图2为单相PWM整流器直接功率控制系统框图。通过功率计算模块对网侧输入电压、电流进行延时及相应计算,获得的网侧有功与无功功率。通过当前网侧有功与无功功率值、直流侧电压及网侧瞬时电压值,可以计算得出当前状态下,不同开关状态对整流器有功与无功功率变化率。同时,可以通过设定的有功与无功功率给定值,计算出各个开关状态作用时间。并构建评价函数来选择出最佳开关状态。图2中,电压外环选用PI控制器,其输出负载电流给定值与直流侧电压相乘之后得到系统功率给定值,输入功率内环控制器后形成负反馈。若直流侧电压低于参考值,则系统功率给定值增大,导致直流侧电压上升,反之亦然,保证系统直流侧电压稳定。

图2 直接功率控制系统框图Fig.2 Direct power control system diagram
将式(3)代入式(2),可得整流器网侧输入端电压对系统功率变化率为
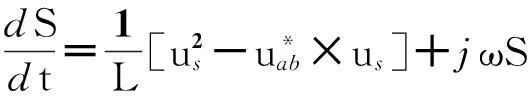
(8)
视在功率S由有功功率P与无功功率Q组成,则由式(3)可将视在功率S进行分解,获得有功功率与无功功率的变化率为
(9)
式中,ω为网侧电压的角频率。
由于系统在控制时需要同时考虑有功功率与无功功率的变化,可引入评价函数
J=(Pk+1-Pref)2+(Qk+1-Qref)2。
(10)
式中:Pk+1、Qk+1为预测下一时刻有功与无功功率Pref、Qref为有功与无功功率设定值。
在单相PWM整流器中,只有3个可选开关矢量(状态),若在单开关周期内采用单一矢量进行控制,会增大系统功率波动,降低系统的控制精度。因此本文采用了有效矢量和零矢量结合的方式的定频控制。先计算每个开关矢量对应最优作用时间,再由评价函数进行判定选择最优的开关矢量及对应的占空比。
图3为系统模型预测控制与开关状态选择算法流程框图。将称开关函数Sab=-1和Sab=1的矢量定义为有效矢量,并称为1矢量和-1矢量;开关函数Sab=0定义为零矢量。单相PWM整流器为boost升压型变换器,则网侧电压的峰值比直流侧电压值小,则系统选用零矢量时,对功率的改变较小,所以因此采用有效矢量与零矢量相结合的方式,以便完成系统功率控制的同时,也能固定开关频率。
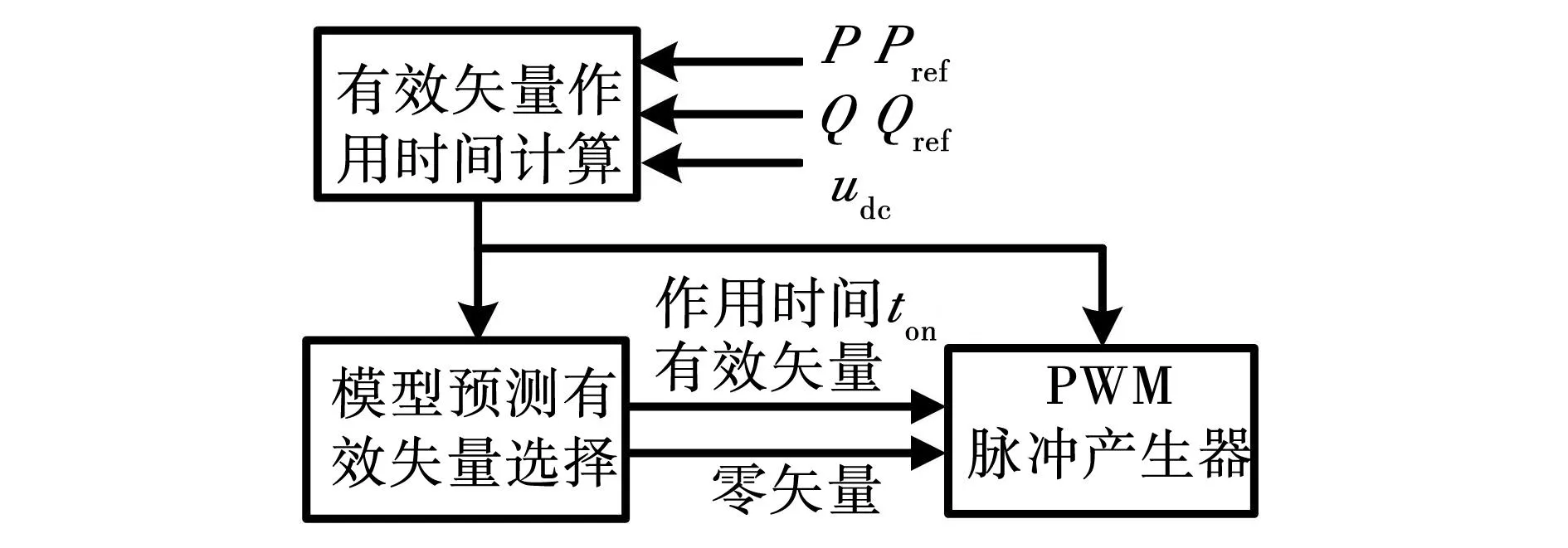
图3 基于占空比优化的模型预测控制算法框图Fig.3 Diagram of model predictive control with duty cycle optimization
2.1矢量对系统功率影响分析
将式(7)代入式(9),采用不同开关矢量对系统有功和无功功率的影响分别如式(11)和(12)所示
(11)
(12)
式中:sP(-1)、sP(0)、sP(1)为3个开关矢量对系统有功功率的影响;sQ(-1)、sQ(0)、sQ(1)为3个开关矢量对系统无功功率的影响。
在当前时刻k,采用任意开关矢量,其对系统功率在下一时刻k+1的都可用式(11)与式(12)表示,当Sab=n(n=-1,1)时,对应k+1时刻系统功率可表示为
(13)
式中:Pk、Qk为当前时刻有功与无功功率;sP(n)、sQ(n)为有效矢量有功与无功增量;Ts、ton(n)为开关周期与有效矢量作用时间。
2.2不同矢量最优占空比求解
由式(13)可知,在k时刻有效矢量作用时间ton(n)的大小决定了k+1时刻功率的大小,由于有功和无功功率是被同一有效矢量所改变,所以ton(n)在取得最优值时,有效矢量n所对应评价函数能够取得最小值。

(14)
式中,J(n)为有效矢量n对应的评价函数。
将式(10)代入式(14),由于此时有功、无功功率实际值与有功、无功功率的设定值都已知,即可求得
(15)
若计算得出有效矢量对应作用时间大于Ts,则ton(n)=Ts,若ton(n)小于零,则ton(n)=0。零矢量的作用时间为t0=Ts-ton(n)。
2.3最优矢量及占空的选择
由此可以计算出两个有效矢量对应的有效矢量作用时间ton(n),将其代入式(13)与式(10)即可以得到当前时刻选择开关矢量对应的评价函数
(16)
比较各个有效矢量所对应的评价函数
Jopt=min(J(-1),J(1))。
(17)
式中,Jopt为最优矢量对应的评价函数。
使用评价函数最小的开关矢量及相应的有效矢量作用时间则可以完成系统有功、无功功率的精确控制。
3仿真与实验研究
为验证所提出的单相PWM整流器MP-DPC算法的有效性和可行性,在Matlab/SIMULINK软件中搭建了仿真模型,对该MP-DPC与传统滞环开关表DPC算法进行了仿真对比验证。并在基于DSP+RT-Lab半实物实验平台上对这两种算法进行了实验对比验证。
3.1仿真研究
表1给出仿真与实验系统参数。
图4给出了稳态情况下两种控制算法对应的有功功率和无功功率仿真波形,两种控制算法电压外环PI参数一致情况下,输出电压在达到设定幅值后,滞环开关表DPC算法对应的有功功率波动约8 kW,无功功率波动约为10 kW,而MP-DPC算法对应的有功功率及无功功率波动都约4 kW,该MP-DPC算法能有效减小稳态功率波动。

表1 仿真与实验系统的主要参数
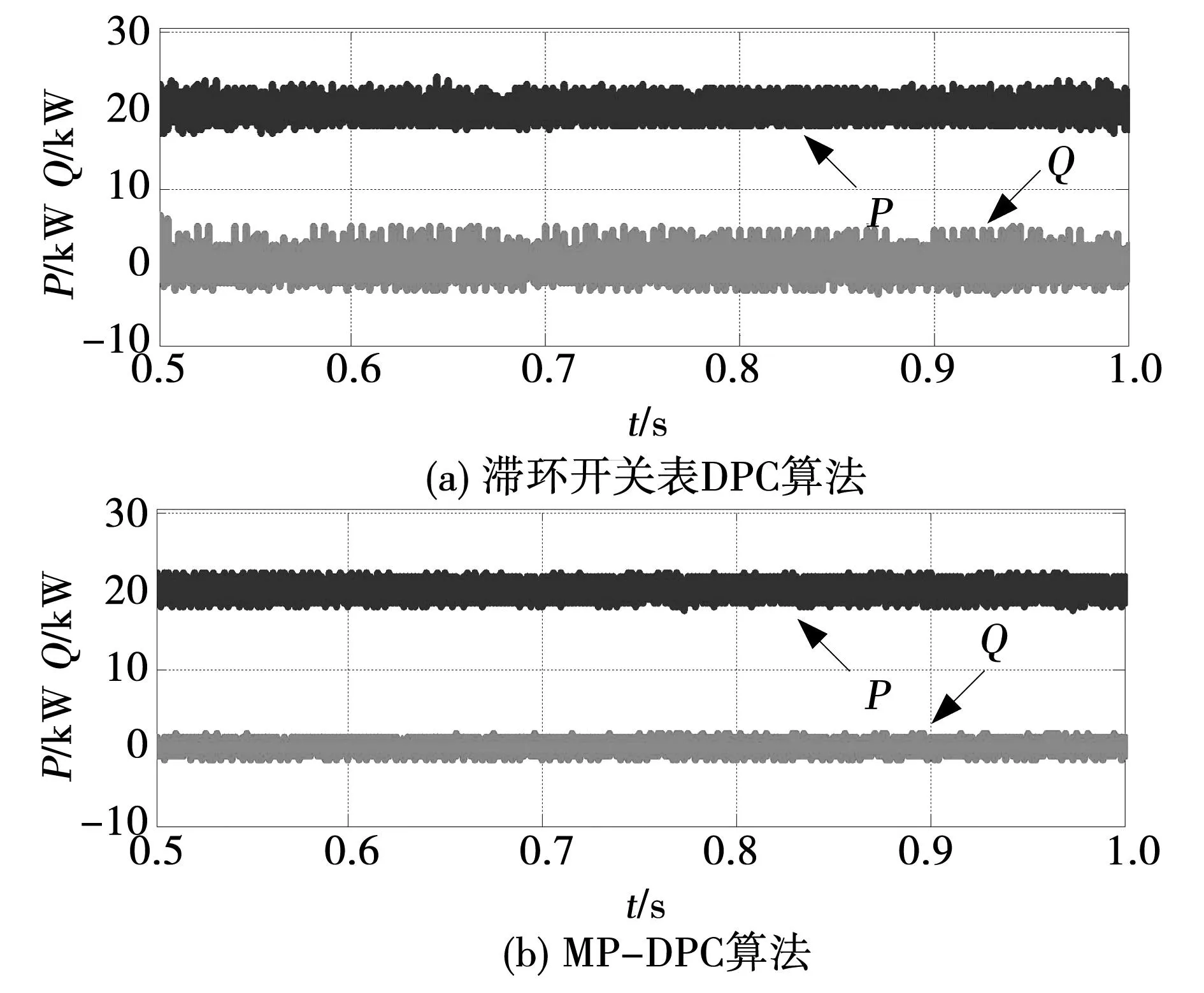
图4 稳态情况下两种算法对应的有功与无功 功率波形Fig.4 Simulation waveforms of active power and reactive power in steady-state
图5(a)和图5(b)分别给出了滞环开关表DPC和MP-DPC算法的网侧电压与电流仿真波形。由图5可知,这两种算法都实现了网侧电压与电流同相位,也即单位功率因数。图6(a)和图6(b)分别给出了两种算法网侧电流的FFT分析结果,由图6可知,滞环开关表DPC算法存在网侧电流谐波含量大,且分布较广泛等缺点。MP-DPC相比滞环开关表DPC,不仅波形畸变率小,谐波含量低,且谐波主要集中在开关频率附近,容易滤除。
为测试控制系统在负载突变时的动态特性,负载在t=1.2 s时由32 Ω突变为16 Ω。图7(a)和图7(b)分别给出了负载突变时滞环开关表DPC和MP-DPC算法的直流侧电压仿真波形。传统滞环开关表DPC算法的功率内环采用查表法进行控制,MP-DPC算法功率内环采用模型预测直接求解方式进行控制,因此这两种算法的功率内环响应速度都非常快,系统的动态特性则大部分依赖于电压外环设定。由图7(a)和图7(b)可以看出两种的动态特性基本一致,也证明该MP-DPC算法保留了滞环开关表DPC快速动态响应的优点。

图5 稳态情况下网侧电压与电流仿真波形Fig.5 Simulation waveforms of the main voltage and the line current in steady-state

图6 网侧电流仿真数据的FFT分析结果Fig.6 FFT analysis results of the line current for two control algorithms in simulation
由图7也可知,负载突变后后稳态时直流侧电压波动明显增大,可知在相同系统参数下,输出功率越大,输出电压的波动越明显。

图7 负载突变时两种算法的直流侧电压波形Fig.7 Simulation waveforms of DC-link voltage under load sudden change condition
图8(a)和图8(b)分别给出了负载突变时滞环开关表DPC和MP-DPC算法的有功与无功功率仿真波形。由图8可知,滞环开关表DPC算法在系统功率增加的同时,无功功率波动也随之加剧,在功率突变的瞬间,MP-DPC算法不但拥有滞环开关表DPC算法优越的动态特性,而且功率波动小。

图8 负载突变时下两种算法的有功与无功功率 仿真波形Fig.8 Simulation waveforms of active and reactive powers when load steps up
3.2半实物实验研究
为了进一步验证理论分析和仿真结果的正确性,本文采用了DSP+RT-Lab半实物实验平台对滞环开关表DPC和MP-DPC算法分别进行了实验对比研究。DSP采用了TI公司的TMS320F2812,RT-Lab实验平台包括一个上位机、两个核心运算单元和多个模拟板与数字板卡:上位机通过以太网线与RT-Lab实验平台相连,能够利用上位机实时观测模型中的多个变量,数字板卡接收DSP发出的脉冲信号,模拟板卡将网侧电压、电流和直流侧电压等信号反馈回DSP,形成完整闭环系统。
在实验中主电路参数设置与仿真一致,如表1所示,图9(a)和图9(b)分别给出了单相PWM整流器稳态工作时滞环开关表DPC算法和模型预测DPC算法的网侧电压、电流与直流侧电压实验波形。

图9 稳态情况下网侧电压与电流、直流侧电压实验波形Fig.9 Experimental waveforms of the main voltage, the line current,and DC-link voltage in steady-state
由图9(a)和图9(b)可知,在稳态情况下,与滞环开关表DPC算法相比,MP-DPC算法中网侧电流波形正弦度更高,且更加光滑,也即谐波含量低。
图10(a)和图10(b)分别给出了滞环开关表DPC和MP-DPC算法对应的网侧电流实验数据的FFT分析结果。由图10可知,滞环开关表DPC算法开关频率不固定,谐波分布广泛。而MP-DPC算法固定了开关频率的同时降低了网侧谐波。

图10 网侧电流实验数据的FFT分析结果Fig.10 FFT analysis results of the line current in experiment
图11(a)和图11(b)分别给出了负载突变时滞环开关表DPC和MP-DPC算法的直流侧电压、有功功率和无功功率实验波形。

图11 负载突变情况下直流侧电压、有功与无功功率 实验波形Fig.11 Experimental waveforms of DC-link voltage, active power and reactive power when load steps up and down
由图11也可知,滞环开关表DPC算法在负载增大后,功率波动也随之加剧,功率纹波较大;与滞环开关表DPC算法相比,MP-DPC算法不但具备同样的动态响应特性,而且功率纹波波动较小。
4结论
本文以单相PWM整流器为研究对象,以固定开关频率、提高系统响应速度、减小网侧电流谐波及保持直流侧电压稳定为研究目标,提出了一种基于占空比调节的单相PWM整流器模型预测直接功率(MP-DPC)控制算法。通过SIMULINK模型仿真与DSP+RT-Lab半实物平台实验对该MP-DPC算法与滞环开关表DPC算法进行了对比研究,研究结果表明,本文所提出的单相MP-DPC算法不但具有网侧谐波小,开关频率固定、功率脉动小等优点,且保留了滞环开关表DPC算法快速动态响应的性能。
参 考 文 献:
[1]马庆安,李群湛,邱大强,等.基于直接功率控制的单相AC-DC变流器控制器设计[J].电工技术学报,2012,27(7): 251-256.
MA Qingan,LI Qunzhan,QIU Daqiang,et al.Single-phase AC-DC converter controller design based on direct power control[J].Transactions of China Electrotechnical Society,2012,27(7): 251-256.
[2]ZHANG Y,LI Z,PIAO Z,et al.A novel three vector based predictive direct power control of doubly fed induction generator for wind energy applications[C]//IEEE Energy Conversion Congress and Exposition,Sept.15-20,2012,Raleigh,USA.2012: 793-800.
[3]ZHI D,XU L.Direct power control of DFIG with constant switching frequency and improved transient Performance[J].IEEE Transactions on Energy Conversion,2007,22(1): 110-118.
[4]宋文胜,冯晓云,谢望玉.单相三电平整流器dq坐标系下的控制与SVPWM方法[J].电机与控制学报,2012,16(4): 56-63.
SONG Wensheng,FENG Xiaoyun,XIE Wangyu.Space vector pulse width modulation and control technique for single phase three level rectifier in d-q coordinate system[J].Electrical Machines and Control,2012,16(4): 56-63.
[5]陈伟.三相电压型PWM整流器的直接功率控制技术研究与实现[D].武汉: 华中科技大学电气工程系,2009: 16-25.
[6]王久和,李华德.一种新的电压型PWM整流器直接功率控制策略[J].中国电机工程学报,2005,25(16): 47-52.
WANG Jiuhe,LI Huade.A new voltage-type PWM Rectifier Power Control Strategy[J].Proceedings of the CSEE,2005,25(16): 47-52.
[7]SATO A,NOGUCHI T.Voltage source PWM rectifier-inverter based on direct power control and its operation characteristics[J].IEEE Transactions on Power Electronics,2011,26(5): 1559-1567.
[8]杨达亮,卢子广,杭乃善,等.三相电压型PWM整流器准定频直接功率控制[J].中国电机工程学报,2011,31(27): 66-73.
YANG Daliang,LU Ziguang,HANG Naishang,et al.Three phase voltage type PWM rectifiers quasi frequency direct power control[J].Proceedings of the CSEE,2011,31(27): 66-73.
[9]乐江源,张志,赖小华.三相并联型有源电力滤波器预测直接功率控制[J].电机与控制学报,2012,16(5): 86-90.
LE Jiangyuan,ZHANG Zhi,LAI Xiaohua.Predictive direct power control of three-phase shunt active power filter [J].Electrical Machines and Control,2012,16(7): 86-90.
[10]杨兴武,姜建国.电压型PWM整流器预测直接功率控制[J].中国电机工程学报,2011,31(3):34-39.
YANG Xingwu,JIANG Jianguo.Voltage source PWM rectifier predictive direct power control [J].Proceedings of the CSEE,2011,31(3):34-39.
[11]徐彬,杨丹,王旭,等.电压型PWM 整流器模糊逻辑功率预测控制策略[J].电机与控制学报,2010,14(8): 52-62.
XU Bin, YANG Dan,WANG Xu,et al.Predictive direct power control strategy based on fuzzy logic for voltage source PWM rectifier [J].Electrical Machines and Control,2010,14(8): 52-62.
[12]ZHANG Y,XIE W.Model predictive mean power control of PWM rectifier[C]// 2013 International Conference on Electrical Machines and Systems,Oct.26-29,2013,Busan,Korea.2013: 2195-2200.
[13]ZHANG Y,XIE W.Model predictive direct power control of a PWM rectifier with duty cycle optimization[J].IEEE Transactions on Power Electronics,2013,28(11): 5343-5351.
[14]张永昌,谢伟,李正熙.PWM 整流器预测无差拍直接功率控制[J].电机与控制学报,2013,17(12): 57-63.
ZHANG Yongchang,XIE Wei,LI Zhengxi.Predictive deadbeat direct power control of PWM rectifier [J].Electrical Machines and Control,2013,17(12): 57-63.
[15]杨君,王兆安,邱关源.单相电路谐波以及无功电流的一种检测方法[J].电工技术学报,1996,11(3): 42-46.
YANG Jun,WANG Zhanan,QIU Guanyuan.A single-phase circuit detection method of harmonic currents and reactive[J].Transactions of China Electrotechnical Society,1996,11(3): 42-46.
[16]LIU J,YANG J,WANG Z.A new approach for single-phase harmonic current detecting and its application in a hybrid active power filter[C]//Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society,Dec.1-3,1999,San Jose,CA.1999,2: 849-854.
[17]MONFARED M,SANATKAR M,GOLESTAN S.Direct active and reactive power control of single-phase grid-tie converters[J].IET Power Electronics,2012,5(8): 1544-1550.
[18]PAVLOU K G,VASILADIOTIS M,MANIAS S N.Constrained model predictive control strategy for single-phase switch-mode rectifiers[J].IET Power Electronics,2012,5(1): 31-40.
[19]唐熊民,朱燕飞,章云.基于功率预测模型的单相PWM整流器直接功率控制[J].控制与决策,2012,27(6): 845-849.
TANG Xiongming,ZHU Yanfei,ZHANG Yun.Single-phase PWM rectifier power prediction model based on direct power control[J].Control and Decision,2012,27(6): 845-849.
(编辑:刘琳琳)
Model predictive power control scheme for single-phase PWM rectifiers with constant switching frequency
SONG Wen-sheng,DENG Zhi-xian
(School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
Abstract:For these drawbacks of traditional switching-table direct power control(DPC) in single-phase PWM rectifiers such as large power ripple,variable switching frequency and large harmonic components of the grid-side current,a single-phase model predictive DPC (MP-DPC) scheme with duty cycle optimization was proposed,on the basis of three-phase model predictive direct power control scheme.Firstly,the grid-side voltage/current rotating vectors were constructed through fictive-axis emulation,and a power calculation algorithm for single-phase system was presented on the basis of instantaneous power theory.Then,combining with the effect of different switching-states on instantaneous power,a MP-DPC scheme with switching-state selection and duty cycle optimization was proposed for single-phase PWM rectifier.Finally,computer simulations and hardware in loop experiments were adopted to test and compare traditional hysteresis switching-table DPC and MP-DPC,respectively.Simulation and experimental results show that the proposed MP-DPC scheme achieves higher precision,lower harmonics and constant switching frequency compared with hysteresis switch-table DPC.Feasibility and correctness of the proposed MP-DPC scheme are also verified.
Keywords:single-phase PWM rectifier; direct power control; model predictive control; duty cycle optimization; hardware in loop experiments
中图分类号:TM 46
文献标志码:A
文章编号:1007-449X(2016)04-0093-08
DOI:10.15938/j.emc.2016.04.013
通讯作者:邓知先
作者简介:宋文胜(1985—),男,博士,讲师,硕士生导师,研究方向为电力牵引交流传动及其控制;邓知先(1991—),男,硕士,研究方向为电力牵引交流传动及其控制。
基金项目:国家自然科学基金(51207131,51277153)
收稿日期:2014-08-08
