双惯量弹性负载系统机械谐振机理分析及谐振特征快速辨识

杨明，　郝亮，　徐殿国

(哈尔滨工业大学 电气工程系，黑龙江 哈尔滨 150001)



双惯量弹性负载系统机械谐振机理分析及谐振特征快速辨识

杨明，郝亮，徐殿国

(哈尔滨工业大学 电气工程系，黑龙江 哈尔滨 150001)

摘要:重点分析带弹性传动装置的双惯量系统机械谐振机理，首先对比连续系统开、闭环幅频特性与固有谐振特征的定量关系，确定谐振模式；进一步针对离散系统，分析控制器刚度对离散闭环系统谐振的影响，确定离散系统持续振荡状态下谐振频率即为NTF频率。通过谐振机理的分析可知固有机械谐振特征对于消除谐振影响显得尤为重要。研究了基于伪随机序列和Chirp信号的两种快速谐振特性获取方法。通过辨识的谐振频率可以确定陷波滤波器参数。仿真及实验结果证实了该谐振特征获取方法的准确性和在此基础上的谐振抑制效果。

关键词:伺服系统；机械谐振；谐振特征辨识；伪随机序列；Chirp信号

0引言

伺服驱动系统的机械部分经常会用到传动轴、联轴器、变速装置等传动装置连接电机与负载。由于实际系统中传动装置弹性系数不是无穷大，尤其是在传动轴细长的情况下，弹性因素的影响不能忽略，就会引发机械谐振[1]。谐振的存在会对系统的机械传动部分造成损害，特别是在中高压大功率电机驱动系统中如果不采取抑制措施可能会产生断轴等严重事故。

早期避免机械谐振的方法很简单，就是降低速度给定的阶跃值或变化斜率，但这必然会限制系统的频响带宽。当前各种研究方案主要针对仅测量驱动电机侧的位置、转速信息，不针对传动装置及负载侧增加传感器。众多的研究方案可大致分为2类：主动方式和被动方式。

所谓主动方式就是用主动改变控制器参数或控制器结构来消除机械谐振。主动方式可分为单纯PI控制(双自由度PI控制、RRC)[2-4]、基于PI的状态反馈控制[5-7]、鲁棒控制、模型预测控制等高级算法应用[8-11]。

所谓被动方式就是在速度环输出与电流环给定之间插入陷波滤波器，而控制系统其他设计不变。利用陷波滤波器衰减指定频率的幅值而对其他频率没有影响的特点，而且其参数设计物理概念明确、简单易行，串入多个陷波滤波器即可抑制多个谐振频率，是目前大规模商用伺服系统普遍采用的方案[12-14]。被动方式又分为在线与离线两种模式：在线模式为在系统运行过程中时刻针对当前谐振情况进行分析获取，自动配置滤波器，占用资源较大，适用于负载变化频繁的弹性传动系统；离线模式首先通过扫频等方法获得系统Bode图，然后通过分析谐振频率特性来设置滤波器参数。离线方式节省控制器资源，适用于负载变化不大的数控机床等。

文献[15]详细阐述了定点算法中所遇到的如延时、量化误差等各种数字信号处理问题。陷波滤波器的通带范围过宽会导致较大的相角滞后，为了增加抑制深度而采用窄通带设计又导致受谐振频带辨识影响加剧，因此，文献[16]采用自适应陷波滤波器设计方案，该方案能够快速辨识谐振中心频率并以此调整滤波器参数设计。尽管陷波滤波器的零极点数目相等对通带范围造成的相角滞后较小，但还是附加了相角滞后，文献[17]通过相角补偿追求零相位滞后，取得一定的效果。

传统获取频率特性的扫频方式精确度较高，但作用时间很长，不利于做低频测试，会造成低频的漂移并增加含谐振系统的机械损害。在文献[18]考虑到用伪随机序列的方法来做扫频。文献[19]提出一种基于Welch法的功率谱估计法。

众多文献针对谐振机理分析不够彻底，即使获取谐振特征后如何设置滤波器参数也没有系统研究。本文分析了带弹性装置的双惯量模型，并对伺服系统中的机械谐振机理进行了研究。分析了连续闭环系统中，控制器刚度对谐振频率的影响。针对离散闭环系统中由于控制器刚度较大引发的稳态持续振荡条件及谐振特性进行了分析，得到陷波滤波器的频率设置选择条件。进一步，通过基于伪随机序列信号及Chirp信号的2种离线谐振特性快速辨识方法来得到准确的谐振特性，为被动方式抑制机械谐振提供准确的谐振参数。

1机械谐振特性分析

1.1谐振原理及模型

电机、传动机构、执行机构组成的典型双惯量机械传动系统如图1所示。其中传动轴系联接电机和执行机构，具有一定的抗扭刚度K和阻尼系数Cw。当传动轴系发生扭转形变时将产生转矩Tw。电机端电磁转矩Te和传动轴系转矩Tw共同作用于转动惯量为J1、阻尼系数为C1的电机转轴。执行机构等效转动惯量为J2、阻尼系数为C2，传动轴系转矩Tw与负载转矩Tl共同作用于执行机构最终决定了负载转速。根据以上分析可建立微分方程组，如式(1)所示[20]。

图1　典型双惯量机械传动装置模型Fig.1　Model of typical 2-mass mechanical system

(1)

可忽略阻尼系数进而对上述微分方程组进行拉普拉斯变换，得

(2)

通过式(2)可以推导出如图2的双惯量传动模型框图，进而推导出电机转速与电机电磁转矩之间的传递函数，如式(3)所示。

图2　传动装置模型框图Fig.2　Block diagram of mechanical transmission

从式(3)中可以得出，机械谐振点在传递函数上引入了一对共轭的零极点，共轭零点为抗谐振频率点ARF(anti-resonance frequency)，共轭极点为自然振动频率点NTF(natural torsional frequency)。零极点的存在使得系统在特定频率下的响应会比较强烈，这就会形成机械谐振现象。通过式(3)可以得到两个谐振点具体频率及惯量比R的关系如式(4)所示。

(4)

1.2连续系统中的谐振

1.2.1开环系统振荡

由于理想电流环具有快速响应性，所以可将速度开环，电流闭环的理想系统近似为谐振模型。通过图2能够得到电机转速与负载转矩间的传递函数见式(5)。由式(3)、式(5)可以得出电机转速与电磁转矩和负载转矩的拉氏表达式及对应的时域单位阶跃响应式，见式(6)、式(7)。

(5)

ωm(s)=G1(s)Te(s)-G2(s)Tl(s)=

(6)

(7)

从式(7)中可以看出开环系统的阶跃响应会在斜坡输出的基础上叠加NTF频率的振荡，振荡幅值与NTF频率成反比。而且振荡频率值与负载转矩无关，所以在分析谐振频率时可以不考虑负载转矩对系统的影响。证明在速度开环情况下，系统会以NTF谐振频率振荡。

1.2.2闭环系统振荡

由于速度环带宽远远小于电流环带宽，可在将电流环近似为1。令速度控制器的传递函数为式(8)时，闭环系统电机转速与速度给定间的传递函数为式(9)，Kp为速度PI控制器比例系数，Ki为速度PI控制器积分系数。

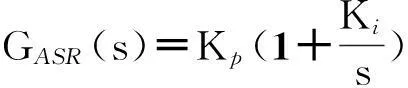
(8)

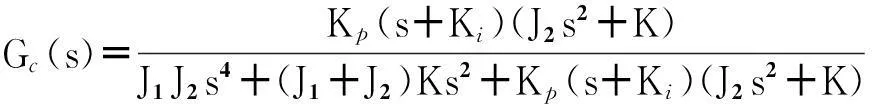
(9)

(s2+2ζ1ω1s+ω12)(s2+2ζ2ω2s+ω22)=0。

(10)

其中ω1和ω2是闭环下的两个自然角频率，ζ1和ζ2为对应频率下的闭环阻尼。可以得到下面四组等式：

(11)

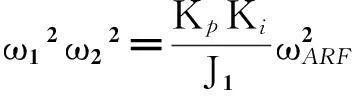
(12)

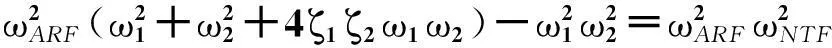
(13)

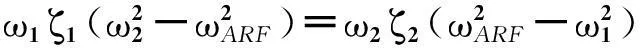
(14)

系统闭环带宽主要受到min(ω1,ω2)的影响，而且通过式(14)发现min(ω1,ω2)<ωARF，所以闭环带宽不会超过ωARF。图3为弹性系统ωm/Te、开环系统及闭环系统的幅频曲线。可以发现由于弹性装置的引入对系统的最显著影响就是降低了系统的带宽，使得系统无法进一步提高性能。

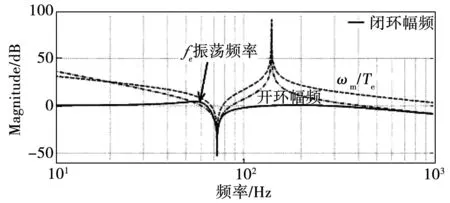
图3　弹性系统幅频特性Fig.3　Magnitude diagram of elastic system

令ωn= min(ω1,ω2)，ζ对应角频率的阻尼。在速度闭环系统中，由于受到闭环控制作用的影响，NTF频率大于0 dB的增益会被明显抑制，所以此时的谐振主要是以接近ARF频率的振荡频率fe在振动，而且该频率振动也会逐渐地趋于稳定。连续闭环系统的振荡频率fe的关系为

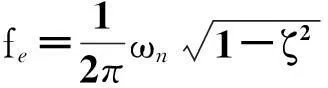
(15)

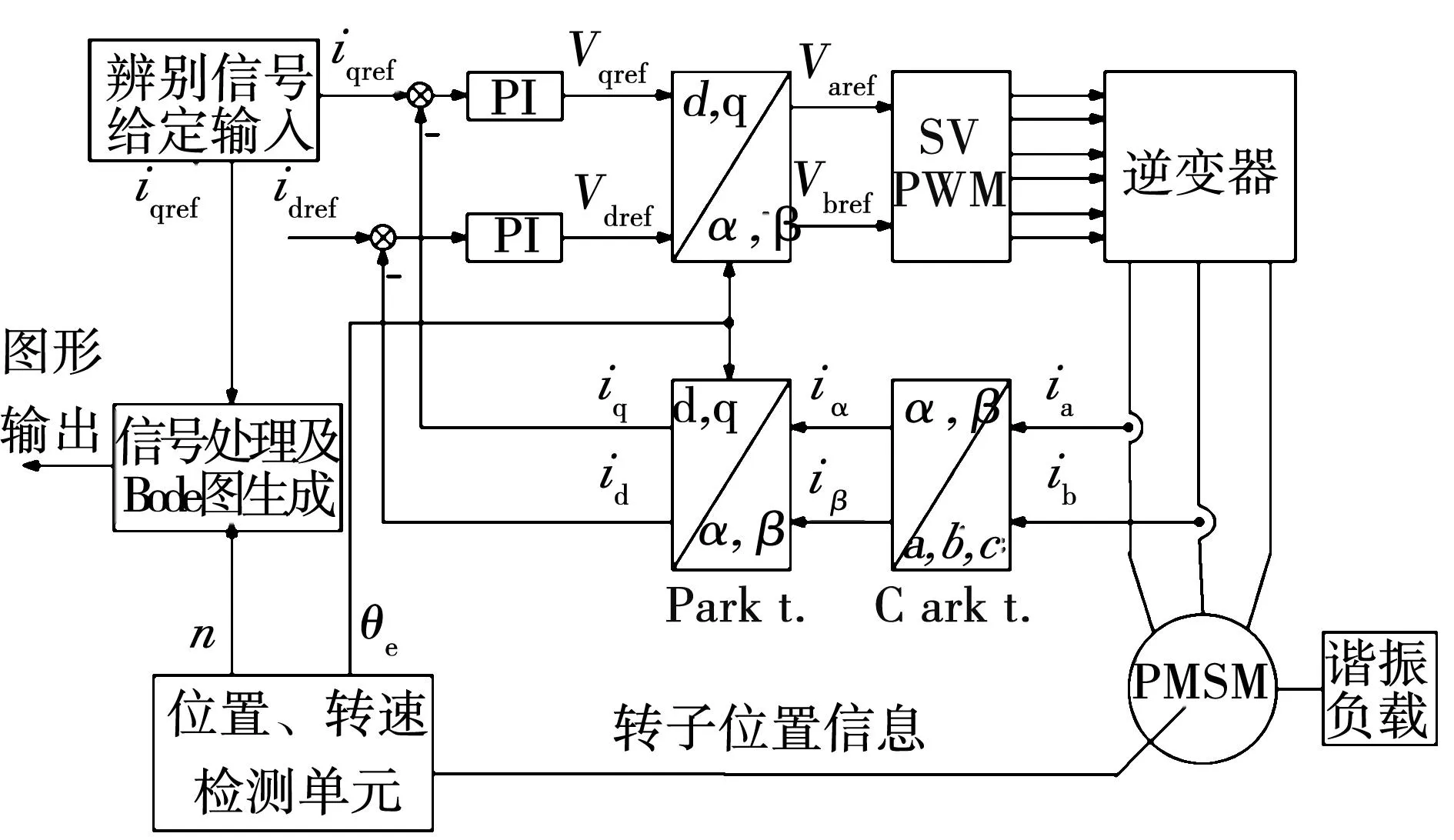
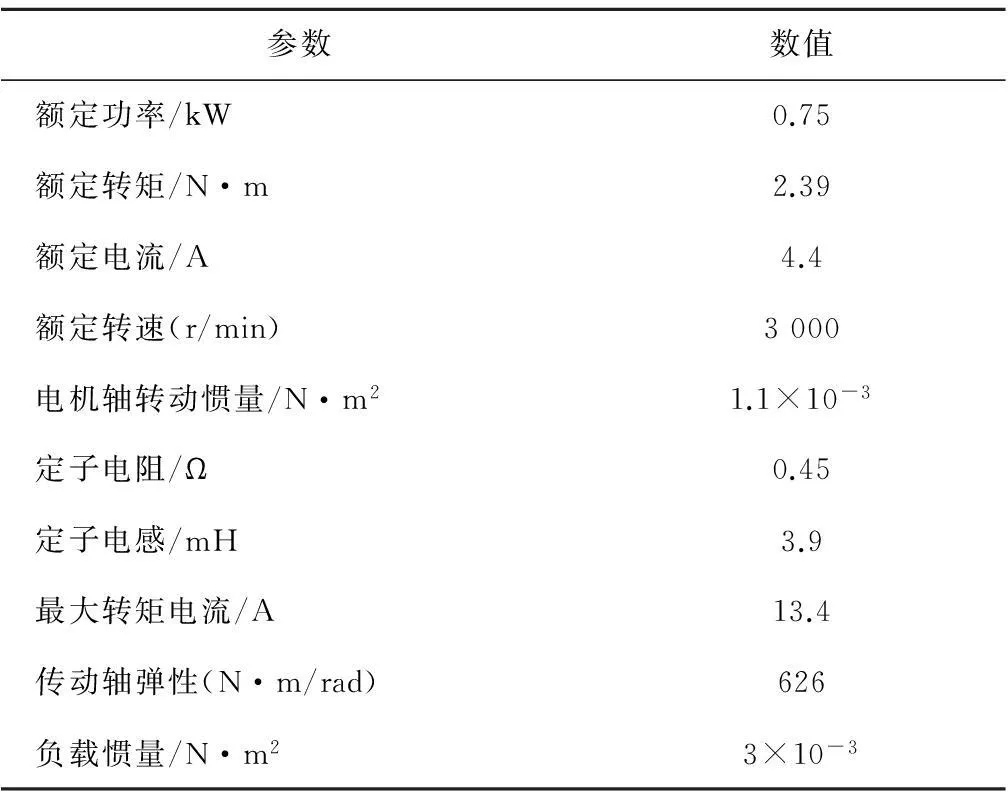
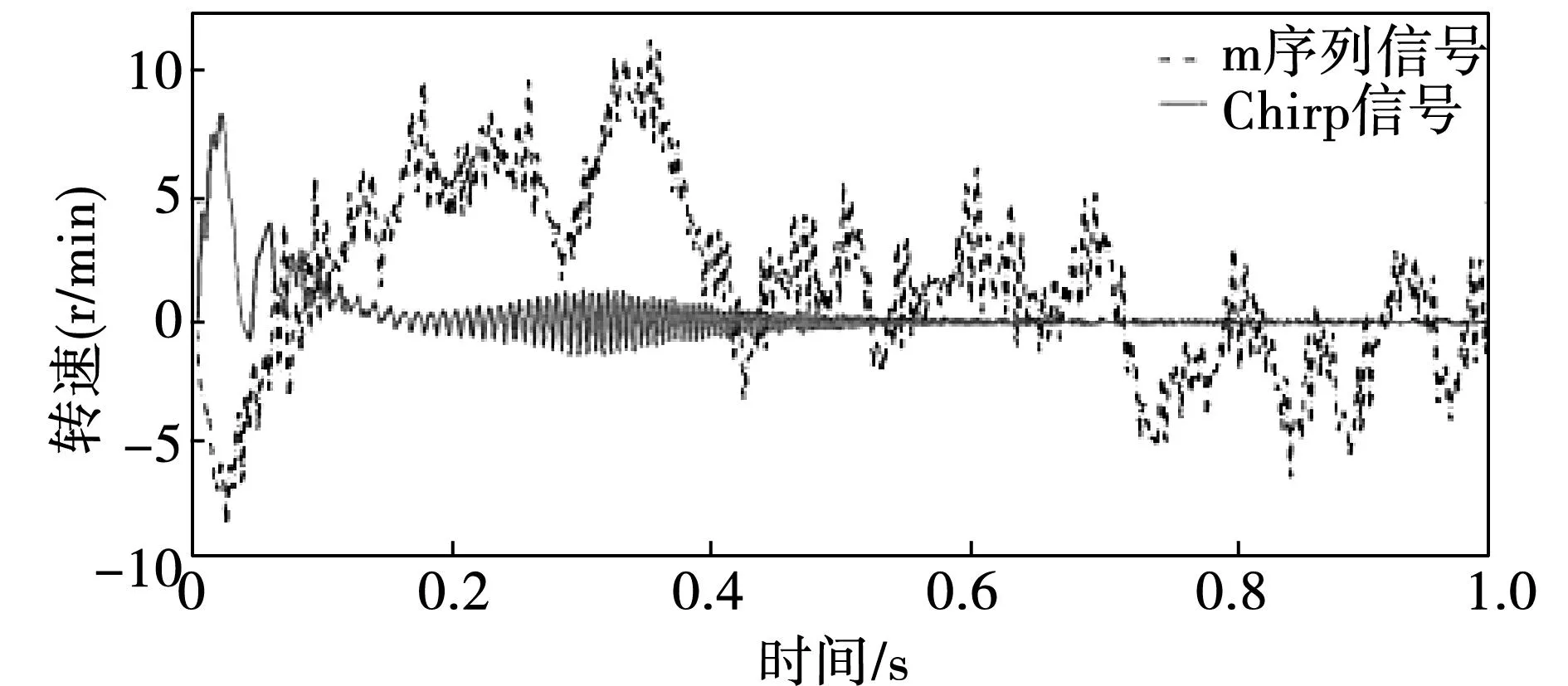
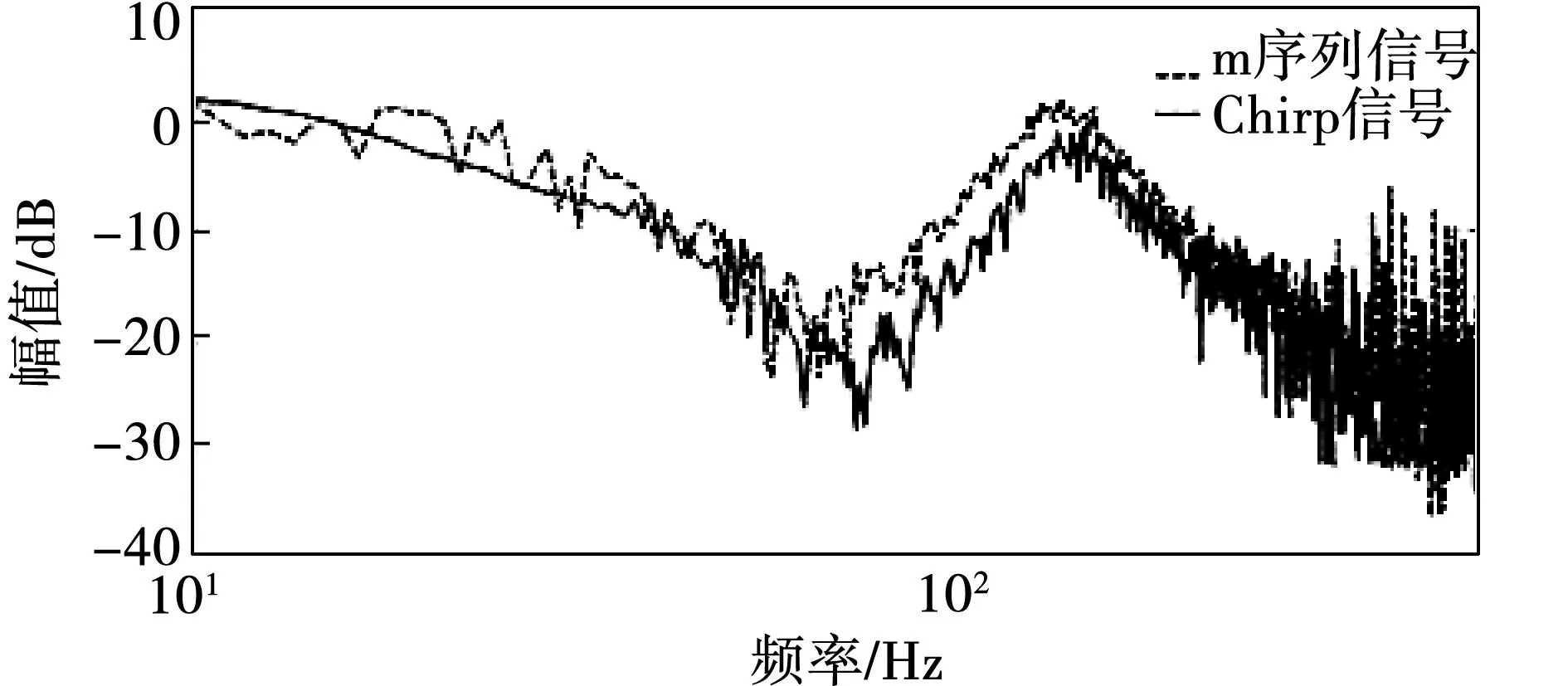
图4为在不同Kp时闭环系统的Bode图，其中Kpa

图4　不同Kp的闭环系统Bode图Fig.4　Bode diagram of closed-loop system with 　　　different Kp

对于过小Kp值的系统，阻尼较大，fe会远离ARF频率。随着Kp的加大，阻尼减小，衰减效果减弱，ωn趋近于ωARF，振荡频率fe接近ARF频率。对于大惯量的数控伺服来说，为了满足动态性能，Kp一般较大，所以在Kp较大的连续系统中，振荡频率fe可以近似为ARF谐振频率。

如图5所示为带有速度输出限幅的闭环系统中速度阶跃响应电机与负载间的转速差振荡。从图5可以看出，振荡频率明显分为两段：当速度调节器饱和，系统处于速度控制开环阶段，此时电机和负载侧都以NTF频率振荡；当电机速度达到给定速度，速度调节器退饱和，进入速度控制闭环阶段。在对于大惯量系统控制器刚度随之较大时，该阶段就能以ARF谐振频率衰减振荡，直至转速达到给定。

图5　扭转振荡的仿真结果Fig.5　Simulation result of torsional oscillation

从振动的类型上看，NTF谐振受到激发后能保持自身特性持续振荡，属于自激振荡；而ARF谐振由于受闭环阻尼的影响，最终会逐渐衰减，属于自由振荡。

1.3离散系统中的谐振

由于实际伺服驱动系统均是数字化控制系统，所以要重点考虑离散化对系统谐振现象的影响。离散化对系统的最直接影响就是改变了系统的相频特性，降低了系统的稳定裕度。除了相角裕度PM，稳定性也可通过增益裕度GM来决定。增益裕度表达式

(16)

其中，A(fg)为穿越-π角度fg频率处的幅值。

在采样1 kHz的离散系统中，由于采样原理，频谱在500 Hz以后就没有确定意义，剪切频率可能无法获得，而变Kp对相频没有影响，所以用GM来判断稳定性更方便。在速度开环情况下，速度Kp决定增益裕度。当GM<0，闭环离散系统发散。图6是两种Kp情况下的速度开环Bode图，连续与离散系统的系统参数一致。

当Kp小于一定值时，系统的增益裕度为正，此时系统具有与连续系统相同的性质。这时，速度控制器不会饱和，仍会在线性范围内，离散系统的谐振情况近似与连续系统一致，逐渐衰减稳定。

图6　不同Kp的开环离散系统Bode图Fig.6　Bode diagram of open-loop discrete　　　 system with different Kp

当Kp增大使增益裕度小于零时，变为发散系统。由于速度控制器的限幅作用使其基本处于饱和状态，振荡形式发生了变化。图7为Kp较大时同一参数下，连续系统与离散系统在速度给定3 000 r/min阶跃的传动轴系振荡对比。从图中可以看出离散后的发散系统会在稳态出现持续谐振。

稳态谐振时控制器在正负饱和间变换，而饱和时的谐振频率为NTF，所以非线性稳态谐振中会包含NTF频率。由于发散系统的稳态振荡是一种幅值变化最剧烈的振荡，所以此时会引入fs/2的附加频率分量(fs为采样频率)。在系统开环截止频率大于附加频率时，系统就会在NTF频率上附加这个谐振频率。图8为不同离散化频率时的对转速差的FFT分解。从图中可以看出，不同采样频率下都会有NTF的谐振频率存在，而且附加的频率为fs/2。

在此情况下，速度控制器参数不再对谐振频率值产生影响。系统处于电流给定均值近似为零的速度开环状态。由于数据保持原理，实际系统在采样后会有一个低通滤波器进行滤波，所以在实际中的该情况下只体现NTF谐振频率。

离散系统一旦由于稳定裕度不满足稳定条件时系统就会发散，而受到控制器限幅的作用使得发散状态受到限制，使得系统变成饱和非线性系统。该饱和非线性形成的稳态振荡同开环NTF振荡一样在激发后不受给定的影响可以持续振荡。

2谐振特征辨识

实际伺服系统的高性能往往要求高控制刚度，Kp一般较大，通过对机械谐振特性的分析可以发现，系统的谐振频率只有ARF及NTF谐振两种情况，而且以NTF谐振为主。由于被动方式的谐振抑制是通过陷波滤波器对谐振频率进行滤波，若系统出现由于稳定裕度不足而导致的稳态持续振荡时，将陷波频率设为NTF频率；反之，没有稳态持续振荡，则可认为衰减振荡，陷波频率设为ARF频率。

图7　连续与离散系统的振荡对比Fig.7　Comparison of oscillation between continuous　　　 and discrete system

研究通过离线方式获取开环系统Bode图来得到谐振特性。图9为离线谐振特性辨识结构框图。信号的给定不宜过小，否则会对辨识精确度造成影响。将信号幅值变为一倍额定电流值输入作为q轴给定输入系统。

2.1辨识给定信号

基础扫频主要是提供频率连续且周期性重复的信号，将不同频率下的系统特性记录下来，以此绘制频率特性曲线。但操作繁琐费时，还可能遗失特定频率的细节，对于谐振系统长时间测试甚至会引发机械损害，所以要研究快速辨识谐振特性的方法。

图8　不同采样频率对谐振频率成分的影响Fig.8　Effects on resonant frequency of different 　　　sampling frequency

图9　离线谐振特性辨识的结构框图Fig.9　Structure block diagram of resonance 　　　characteristic identification in discrete　　　 system

快速系统辨识中给定信号的最主要特点是要能充分包含所有的频率成分，频域上有宽频谱，时域上信号变化剧烈呈现非周期性。符合该特点的信号最典型的就是白噪声信号，但由于白噪声不易在实际的数字系统中实现且噪声方差较大，所以需要通过其他符合辨识特点的信号来代替。

2.1.1伪随机序列信号

伪随机序列码就能充分体现辨识信号特点。用到的伪随机序列码为m序列码，m序列又称最大线性移位寄存器序列，它的产生是由反馈移位寄存器生成的。序列x1x2…xpxp+1…，各元素间存在式(17)的关系：

xi=a1xi-1⊕a2xi-2⊕…⊕apxi-p,i=p+1,p+2,…

(17)

其中ai取0或1，⊕表示求和模2运算。

二进制m序列具有良好的伪随机特性，有以下几个特点：

1)平衡性：二进制m序列的一个周期中，1与0的数目相差1。

2)具有二值自相关函数。

对于一个周期为T=2n-1的±1电平m序列，n为m序列的阶数，其自相关函数为

(18)

其中u(k)为序列信号电平值，τ为整数。

这样得到的自相关特性为：当τ为0和T的整数倍时R(τ)=T，τ取其他值时为弱相关R(τ)= -1，当周期T很大时，m序列的自相关函数与白噪声类似，这样就有很尖锐的自相关特性，这就是可以选择基于m序列的伪随机序列来代替白噪声做电流给定信号的原因。

二位式m序列的一个周期中1的个数比-1的个数只多一个，序列的平均值很小，在实际应用中避免了开环下的低速累积导致的速度过大问题。图10序列作为q轴电流给定的波形图。

图10　伪随机序列信号波形图Fig.10　Waveform graph of Pseudo random　　　 sequence signal

2.1.2Chirp信号

除了伪随机序列信号以外，Chirp信号也具有宽频带及恒定频率分量值。Chirp信号为调频脉冲扫频信号，是一种连续的余弦扫频信号。在频率特性获取中，用的是如下

u(t)=Acos(2π(βt2+f0t))。

(19)

其中A为扫频幅值，β为频率变化速率，f0为初始频率。由式(19)可以看出Chirp信号是随时间线性变化的余弦函数，其作为q轴电流给定的波形图见图11。

通过对Chirp信号的FFT分解可以发现，该信号也有类似白噪声的统一的频率分量，也可以产生宽范围的频带。Chirp信号频带有截止范围，取决于信号的高频中止频率，频率越高，频带越宽。

以上两种辨识信号都具有快速性和准确性，在采样1 kHz的离散系统中，只需1 s即可完成信号给定。

图11　Chirp波形图Fig.11　Waveform graph of Chirp signal

2.2数据处理

由于给定x(t)引起的激励y(t)，它的傅里叶变换y(jω)等于系统传递函数G(jω)和x(jω)的乘积，即

y(jω)=G(jω)·x(jω)。

(20)

通过FFT运算可以得到给定信号及激励信号的相同频率ωr的同相正交分量，为

(21)

通过计算每个频率处的给定信号与激励信号的幅值比和相位差就可以得到被测系统的幅频和相频特性。系统的幅频及相频特性可按下式(22)计算。按上述方式就可以绘制出系统的频率特性Bode图。

(22)

3仿真与实验

3.1仿真结果

在Matlab/SIMULINK中进行仿真验证，仿真中用到的永磁同步伺服系统参数如表1。

在此系统参数下可以算出ARF=72 Hz，NTF=140 Hz。图12为m序列信号及Chirp信号两种给定方式的对比图。通过仿真对比图可以发现，两种信号给定都能获得开环系统的频率特性(本文只列出幅频特性)，但Chirp信号得到的结果要优于m序列信号，噪声方差含量较小。

3.2实验结果

图13为双惯量系统实物图，左右两侧电机可互为电机-负载结构，中间以弹性轴联接，并可通过附加中间的惯量盘达到改变负载惯量的目的。实物系统参数与仿真一致。

表1　永磁同步伺服系统主要参数

图12　两种信号FFT法仿真结果Fig.12　Simulation results between two signals 　　　with FFT method

图13　双惯量系统实物图Fig.13　Realtest bench of 2-mass system

在实物平台上用以上方法获取系统机械谐振特性。两种信号给定与速度检测采样的频率都为1 kHz，信号长度为1 024，所以给定时长1 s，加上FFT运算共计1.07 s即可得到谐振特性Bode图。图14为两种方法的电机侧转速波形。两种方法都具有运行时间短、没有转速累加的优点，均可以避免长时间运行和高转速时谐振对系统的机械损害。

图15为两种信号用FFT直接计算法的实物对比结果图。两种方法均能得到谐振特性，实验证明其在谐振特性获取上的可行性及实用性。

图14　两种方法的电机转速波形Fig.14　Waveform of motor speed between two methods

图15　两种信号FFT法实物结果Fig.15　Real results between two signals with　　　 FFT method

图16是在不改变控制器参数情况下，改变弹性轴系数并增加电机惯量的对比图，用的是Chirp信号法。其中轴刚性增加，弹性系数为2 190 N·m/rad，电机惯量为5.9×10-3N·m2，负载惯量不变为3×10-3N·m2，进而算出的理论ARF为136 Hz，NTF为167 Hz。可以看出不同参数不会对辨识造成影响，该快速辨识方法具有很好的精确度。

图16　改变轴刚度系数实物结果Fig.16　Real results of changing stiffness coefficient

由于离散系统出现持续振荡现象，证明稳定裕度不足，根据前面的分析谐振频率为NTF频率。通过幅频特性图可以读出当前NTF谐振频率，依据该频率配置陷波滤波器的陷波频率。将陷波滤波器设置在速度控制器输出后进行滤波处理，可以得到滤波前后的转速阶跃对比图，见图17。实验证明根据辨识后的谐振特征可以确定陷波滤波器参数，达到抑制机械谐振的目的。

图17　根据辨识特征投入陷波滤波器前后实物对比Fig.17　Comparison before and after setting notch 　　　filter according to identification of　　　 characteristics

5结论

为了能离线获取机械谐振特性，本文分析了连续及离散系统的谐振特性并提出了实用的谐振特性辨识方法。得到如下结论：

1)闭环系统的带宽受到弹性系统的限制，加大连续系统刚度只会使系统带宽及谐振频率趋近ARF谐振频率。所以在大惯量伺服系统中，由于控制器刚度较高，可以将谐振频率近似为ARF频率。

2)由于刚度的增加可能会使离散闭环系统的稳定裕度为负，进入发散状态。由于速度限幅的作用，使系统进入非线性振荡状态。此时振荡频率为NTF频率叠加二分之一采样频率，经过采样滤波的实际系统体现的就为NTF谐振频率。

3)通过伪随机序列信号或Chirp信号的FFT直接运算法可以得到谐振特性的Bode图。辨识方法具有快速性，以及小转动量的特点，可以降低对谐振系统的机械损害，提高测试的安全性。

参 考 文 献:

[1]马小亮．驱动弹性负载的调速传动[J]．电气传动，2008，38(7)：3-7．

MA Xiaoliang .Variable speed drives with elastic loads[J].Electric Drive,2008,38(7): 3-7.

[2]G Zhang．Speed control of two-interia system by PI/PID control [J].IEEE Transactions on Industrial Electronics,2000,47(3)：603-609．

[3]S KATSURA，K OHNISHI．Force servoing by flexible manipulator based on resonance ratio control[J]．IEEE Transactions on Industrial Electronics，2007，54(1)：539-547．

[4]Y HORI，H SAWADA，Y CHUN．Slow resonance ratio control for vibration suppression and disturbance rejection in torsional system[J]．IEEE Transactions on Industrial Electronics，1999，46(1)：162-168．

[5]K SZABAT，T ORLOWSKA-KOWALSKA．Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks-comparative study[J]．IEEE Transactions on Industrial Electronics，2007， 54(2)：1193-1206．

[6]G.Shahgholian，P.Shafaghi，M.Zinali，S.Moalem．State space analysis and control design of two-mass resonant system[C]//2009 Second International Conference on Computer and Electrical Engineering,2009:97-101.

[7]T ORLOWSKA-KOWALSKA，M KAMINSKI．Effectiveness of saliency-based methods in optimization of neural state estimators of the drive system with elastic couplings[J]．IEEE Transactions on Industrial Electronics，2009，56(10)：4043-4051．

[8]A.Hace，K.Jezernik，A.abanovic．SMC with disturbance observer for a linear belt drive[J]．IEEE Transactions on Industrial Electronics，2007， 54(6)：3402-3412．

[9]K.Peter，I.Schöling，B Orlik．Robust output-feedback H∞-control with a nonlinear observer for a two-mass system[J]．IEEE Transactions on Industry Applications，2003，39(3)：637-644．

[10]M CYCHOWSKI，K SZABAT，T ORLOWSKA- KOWALSKA．Constrained model predictive control of the drive system with mechanical elasticity[J]．IEEE Transactions on Industry Applications，2009，56(6)：1963-1973．

[11]P J SERKIES，K SZABAT．Application of the MPC to the position control of the two-mass drive system[J]．IEEE Transactions on Industrial Electronics，2013，60(9)：3679-3688．

[12]G ELLIS，R D LORENZ．Resonant load control methods for industrial servo drives[C]//Industry Applications Conference，2000，3：1438-1445．

[13]Wei-Chih Hsu，Chien-Liang Lai，Pau-Lo Hsu．A novel design for vibration suppression for lightly-damped servo control systems[C]//Proceedings of 2011 8th Asian Control Conference (ASCC)，2011，251-256．

[14]P SCHMIDT，T REHM．Notch filter tuning for resonant frequency reduction in dual inertia systems[C]//IAS Annual Meeting (IEEE Industry Applications Conference)，1999，3：1730-1734．

[15]Lennart Harnefors．Implementation of resonant controllers and filters in fixed-point arithmetic[J] ．IEEE Transactions on Industrial Electronics，2009，56(4)：1273-1281．

[16]C I KANG，C H KIM．An adaptive notch filter for suppressing mechanical resonance in high track density disk drives[J]．Microsystem Technologies，2005，11：638-652．

[17]S KUMAGAI，K OHISHI，T MIYAZAKI．High performance robot motion control based on zero phase error notch filter and D-PD control[C]//Proceedings of 2009 IEEE International Conference on Mechatronics，2009，1-6．

[18]JENNISONB K.Performance of a linear frequency modulated signal detection algorithm[C]// The Record of the IEEE 2000 International，2000: 447-450.

[19]VILLWOCK S,PACAS M.Application of the welch-method for the identification of two- and three-mass-system[J].IEEE Transactions on Industrial Electronics,2008:457-466.

[20]杨明，胡浩，徐殿国．永磁交流伺服系统机械谐振成因及其抑制[J]．电机与控制学报，2012,16(1)：79-84．

YANG Ming,HU Hao,XU Dianguo.Cause and suppression of mechanical resonance in PMSM servo system[J].Electric Machines and Control,2012,16(1)：79-84.

(编辑：刘素菊)

Analysis of mechanical resonance mechanism and fast identification of resonance characteristic for 2-mass system with elastic load

YANG Ming,HAO liang,XU Dian-guo

(Department of Electrical Engineering,Harbin Institute of Technology,Harbin 150001,China)

Abstract:Mechanism of mechanical resonance in two-mass system with elastic transmission was analyzed.First of all,the quantitative relation between magnitude characteristic of open/closed-loop continuous system and natural resonant characteristic was contrasted.According to the relation,the resonant mode was confirmed.In discrete system,the effect of controller’s rigidity on oscillation in closed-loop discrete system was analyzed.The resonant frequency at the state of sustained oscillation in discrete system is NTF.Through the analysis of resonance mechanism,the natural resonant characteristic is important to eliminate resonance.Two methods of fast acquirement of resonant characteristic were discussed based on Pseudo random sequence and Chirp signals.According to the identified frequency,the parameter of notch filter was determined.The results of simulation and experiment demonstrate the accuracy of this method and the suppression effect based on this method.

Keywords:servo system; mechanical resonance; identification of resonance-characteristic; Pseudo random sequence; Chirp signal

中图分类号:TM 921

文献标志码:A

文章编号:1007-449X(2016)04-0112-09

DOI:10.15938/j.emc.2016.04.016

通讯作者:杨明

作者简介:杨明(1978—)，男，博士，副教授，博士生导师，研究方向为永磁交流伺服系统；徐殿国(1960—)，男，博士，教授，博士生导师，研究方向为电力电子技术，交流电机驱动。

基金项目：国家自然科学基金(61273147)

收稿日期:2014-03-30

郝亮(1989—)，男，硕士，研究方向为伺服驱动控制；