连续梁桥水平转体过程中振动加速度与整体稳定性的关系研究

魏赞洋， 张文学， 黄 荐， 刘海陆

（北京工业大学 建筑工程学院，北京 100124）

随着我国交通路网的进一步升级，跨线工程逐渐增多。水平转体法因具有对既有线下交通干扰小、场地适应能力强等特点而成为跨线桥施工的首选方案。然而结构在转体过程中要承受阵风和转动诱发振动等不确定作用［1－3］，不可避免地产生振动响应。当激励作用为特定频率时引发共振，对整体稳定性构成威胁。

为确保桥梁水平转体过程中的安全，有必要对转体结构进行稳定性实时监控。而当前主流的转体施工监测方案仅包括转体前后控制截面应变监测、主梁线形监测、转体前不平衡力矩测试等［4］，尚没有反映整体稳定性的监控变量。出于对稳定性实时监控的需求，部分转体工程的监测方案中加入了振动监测［5］。相对于通过直接测量墩底应力监控方案，振动监测有不受局部材料离散性影响、传感器反应灵敏、数据可信度高等优点。目前桥梁结构振动的研究已经应用于成桥健康监测和索结构桥梁施工阶段的振动控制［6－17］。而转体结构振动监控变量与整体稳定的关系尚缺乏研究，多凭经验进行主观判定，振动监测结果难以定量地反映结构的倾覆危险程度，不可避免地存在安全隐患。因此本文结合桥梁水平转体施工的特点和相关工程经验，提出了监测振动加速度间接获得墩底弯矩进而实现整体稳定性监控的思想。

为了揭示转体结构的振动加速度与墩底弯矩间的关系，通过实测转体结构振动数据结合有限元分析获得一般转体结构的振动规律，并推导转体结构以纵桥向立面内非对称振型振动时振动加速度与墩底弯矩比值的解析公式。最后在此基础上给出客运专线常见桥梁平转过程振动加速度限值的推荐计算公式及相应表格，以便为同类工程的转体施工监控提供参考。

1 转体过程振动特性分析

为研究连续梁桥转体结构的振动特性，对大西客运专线上院跨朔黄铁路特大桥转体过程振动进行了实测。大西客运专线设计时速250km／h，预留350 km／h。上院跨朔黄铁路特大桥主桥为60m＋100m＋60m连续箱梁，转体结构墩高20m，上转盘尺寸16.4m×10.8m×3.7m，上球铰平面直径4.1m，下球铰平面直径3.8m，撑脚滑道中心线半径4.5m。

1.1 模态分析

采用有限元软件对上述转体结构进行模态分析。由于只关注纵桥向立面内的振动，建立二维平面模型。约束墩底节点的平动位移，放松转动位移，模拟上下转盘连接。约束单侧上转盘单元端部节点的竖向平动位移模拟撑脚。模态参数见表1，模态分析结果中转体结构前3阶振型见图1。

表1 模态参数

图1 上院跨朔黄铁路特大桥转体结构振型

1.2 实测振动数据分析

振动监测采用891－4型拾振器，布置于转体结构悬臂梁端，测量竖向振动。转体过程振动监测历时1 780s，采样频率255Hz。转体结构实测位移时程分布和转换到频域的分布见图2。

对照表1和图2可知，频域分布图中的3个峰值频率分别对应转体结构纵桥向立面内前3阶振型的振动频率；第3阶振型频率之后再无峰值，可认为更高阶的振型对转体结构的实际振动影响很小，可以忽略。由图1可见第2阶振型为对称振型，该振型对墩底弯矩没有影响，所以转体结构墩底弯矩主要受纵桥向立面内的前2阶非对称振型控制。

图2 上院跨朔黄铁路特大桥转体过程实测位移时域与频域分布

2 墩底弯矩与振动加速度的关系推导

为得到结构以纵桥向立面内特定非对称振型振动时墩底弯矩M 与振动加速度a的关系，推导a与M比值的解析公式。

根据无限自由度体系的自由振动规律，二维平面内单一振型振动下，轴线与x轴重合的等直杆上任意点的横向位移y 可由式（1）描述［18］。

式中：ω为振型频率；Y（x）为振型函数。

令λ4＝ω2／（EI），则Y（x）通解为

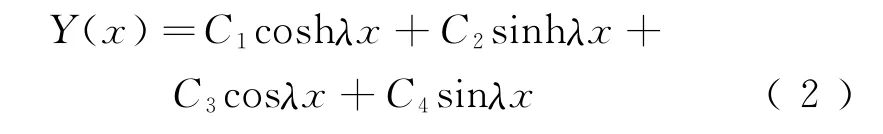
对于二维梁单元，2节点分别编码为i、j。不考虑单元轴向变形。约束i端平动位移yi，则杆端力与杆端位移有如下关系

将转体结构桥墩编为1号构件，简化为梁单元，墩底为i端、墩梁结合端为j端。将右侧悬臂梁编为2号构件，简化为无限自由度等直杆，桥墩与梁的轴线交点为悬臂梁局部坐标的原点，向右为x2轴正方向，向下为y2轴正方向。假定左侧悬臂梁变形与右侧悬臂梁反对称，不单独考虑。由于一般转体结构梁高较大，墩顶至主梁重心的高差不可忽略，故将此高差段简化为刚臂。上转盘简化为转动弹簧，转动刚度为k。转体结构体系简图见图3。

图3 转体结构体系简图

基于以上假定，可以采用悬臂梁上任意点竖向位移y2、悬臂梁顺桥向位移X2和墩底转角θ1i描述转体结构振动形态。表达式分别为

式中：C5～C10为待定系数。

对于转体结构应符合如下边界条件：

（1）悬臂梁自由端弯矩恒为0，即¨Y2（L2）＝0，则

（2）悬臂梁自由端剪力恒为0，即Y···2（L2）＝0，则

（3）悬臂梁在与桥墩连接点竖向位移恒为0，即Y2（0）＝0，则

（4）墩顶剪力平衡

取两个悬臂梁为隔离体，根据牛顿第二定律，对于隔离体，满足

由已知条件可知水平外力F为

桥墩单元采用集中质量，并考虑用于校准主梁总质量的修正质量ms，则隔离体质量

隔离体水平加速度a为

对于桥墩单元墩顶剪力F1j为

式中：E1为桥墩混凝土弹性模量；I1为桥墩截面惯性矩。

墩顶转角θ1j为

墩顶水平位移y1j为

主梁重心与墩顶高差hk为

式中：h0为悬臂梁根部的截面高度；hz为悬臂梁中点处截面高度。

将式（6）、式（15）、式（16）代入式（14）得到墩顶剪力F1j的表达式，与式（11）、式（12）、式（13）一并代入式（10）并简化整理得到

（5）墩顶弯矩平衡

根据墩梁结合处弯矩平衡条件，有

悬臂梁根部弯矩M2为

式中：E2为悬臂梁混凝土弹性模量；I2为悬臂梁截面惯性矩。

对于桥墩单元墩顶弯矩M1j为

将式（6）、式（15）、式（16）代入式（21）得到墩顶弯矩 M1j的表达式，与式（12）、式（13）、式（20）代入式（19）得到

（6）墩底弯矩平衡

转体结构通过上转盘固定于基础上。将上转盘视为一个转动弹簧，则

式中：k为上转盘转动刚度。

对于桥墩单元墩底弯矩M1i为

将式（6）、式（15）、式（16）代入式（24）得到墩底弯矩M1i的表达式，再与式（15）一并代入式（23）得到

最终，由式（7）～式（9 ）、式（18）、式（22）和式（25）得到关于C5～C10的线性方程组，方程组的行列式如下

C5～C10不全为0，则方程组行列式＝0。将＝ω2／（E2I2）代入方程组得到一个关于ω的方程，即可解得各阶振型频率ω。将所关注振型的ω回代入（26）解线性方程即可求得C5～C10。

根据工程经验，适合测量的转体结构振动物理量为墩顶顺桥向水平加速度ah和悬臂梁端竖向加速度av，分别为

将ω 和C5～C10代入式（24）、式（27）、式（28），再代入式（29）、式（30）得到墩顶顺桥向水平加速度与墩底弯矩的比值μ和悬臂梁端竖向加速度与墩底弯矩的比值μ′，即

3 有限元验证

为验证上述解析公式的可靠性，选用速度为350 km／h客运专线4种常用跨径的双线连续梁桥作为依托工程，建立转体结构有限元模型。上部结构参考文献［19］。下部结构参照郑徐客运专线实际工程，桥墩采用C35混凝土，上转盘采用C50混凝土。下部结构几何参数见表2。

计算4个跨径的转体结构在墩高分别为10、20、30、40m时纵桥向立面内前2阶非对称振型振动中悬臂梁端竖向加速度和墩顶顺桥向加速度与墩底弯矩的比值。

表2 下部结构几何参数

采用时程分析，激励荷载从撑脚端部节点竖向自由度输入，波形为正弦波，正弦波频率为所验算振型的频率。材料参数参照文献［20－21］。

解析公式计算参数依照如下公式取值。

（1）桥墩均布质量

式中：A1为桥墩截面面积；ρ为桥墩混凝土重度；g为重力加速度。

（2）主梁等效均布质量按照主梁转动惯量等效原则计算，即

式中：为主梁等效均布质量；mi为标准图中转体结构部分第i节段质量；Li为标准图中转体结构部分第i节段重心到桥墩中心线的距离。

（3）修正质量以主梁总质量相等原则确定，即

（4）上转盘转动刚度

式中：E为上转盘混凝土弹性模量；I为将上转盘简化为连接墩底与撑脚、轴线方向为纵桥向的梁单元后，以上转盘横桥向尺寸为宽并以上转盘厚度为高的矩形截面惯性矩；L为撑脚滑道中心线半径。

依照以上公式计算得到的4种跨径的转体结构参数见表3。

表3 4种跨径的转体结构参数

各跨径转体结构加速度与墩底弯矩比值随墩高变化的解析曲线与有限元计算结果，转体结构以第1阶非对称振型振动时见图4、以第2阶非对称振型振动时见图5。可知，对于不同转体结构的第1阶非对称振型，解析公式能够较好地描述加速度与墩底弯矩的关系。对于第2阶非对称振型，悬臂梁端竖向加速度与墩底弯矩比值的解析公式与有限元结果存在一定偏差。而墩顶顺桥向加速度与墩底弯矩比值的解析公式结果在墩高20m以上时与有限元结果符合较好。鉴于一般情况下跨线桥墩高不小于15m，且解析公式结果偏小，在实际应用中偏于安全。同时考虑到墩顶顺桥向加速度不受对称振型的干扰。推荐使用墩顶顺桥向加速度计算墩底弯矩。

4 加速度限值推荐公式

为了将以上结论应用于实际工程，给出墩顶顺桥向加速度限值的计算公式，以便明确地依照加速度值判定结构的危险程度。

图4 转体结构以第1阶非对称振型振动时加速度与墩底弯矩的比值与墩高关系曲线

将转体结构的振动简化为处于纵桥向立面内的前2阶非对称振型振动的叠加。由于目前尚无法考虑2阶振型的相位差，所以偏安全地假定2阶振型的峰值按绝对值叠加。则转体结构墩顶顺桥向水平加速度限值ad的推荐公式为

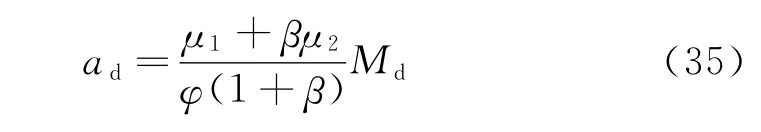
式中：μ1、μ2分别为第1、2阶振型加速度与墩底弯矩的比值，参见式（29），对于速度为350km／h客运专线的转体结构可按表4、表5插值取用；β为墩底弯矩中第2阶非对称振型与第1阶振型所占成分的比值，按照实测经验取1.0～3.0；Md为转动装置设计容许弯矩；φ为安全系数，根据有限元计算结果，建议取2.0。

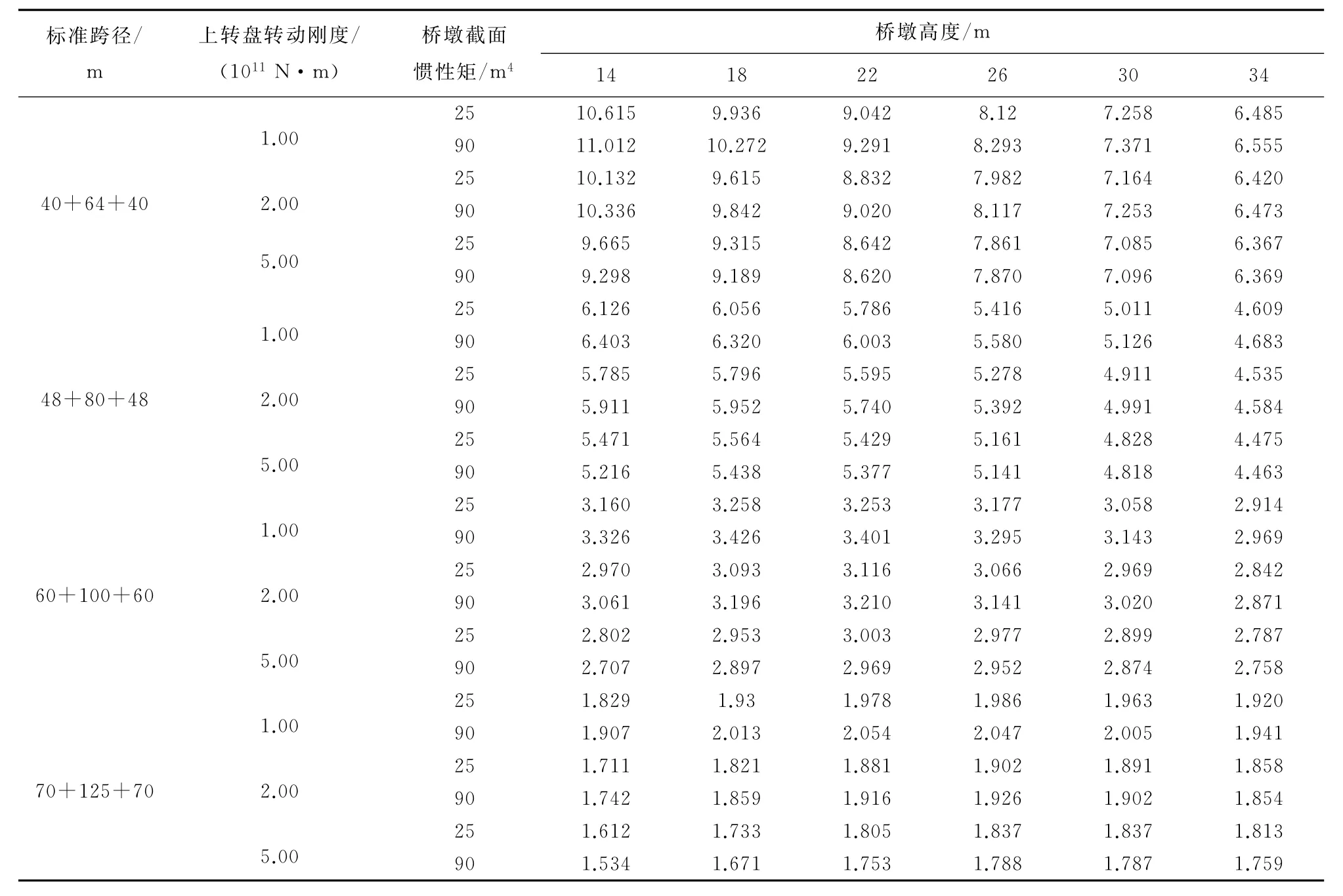
表4 速度为350km／h客运专线转体结构以第1阶非对称振型振动时加速度与墩底弯矩的比值 10－6 s－2·kN－1

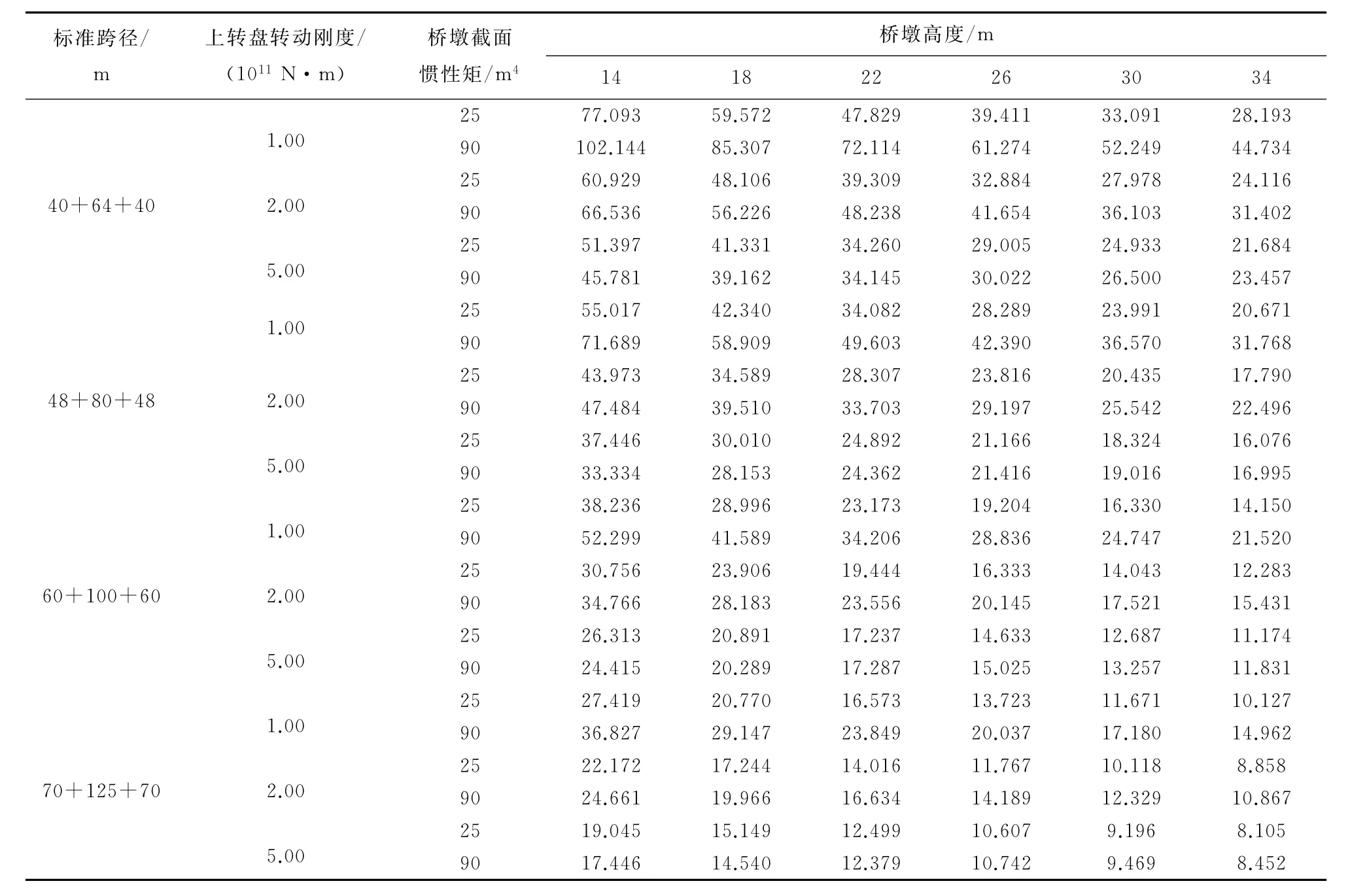
表5 速度为350km／h客运专线转体结构以第2阶非对称振型振动时加速度与墩底弯矩的比值 10－6 s－2·kN－1

5 结论

（1）转体结构墩底弯矩主要受纵桥向立面内的前2阶非对称振型影响。

（2）将主梁简化为无限自由度等直杆、将桥墩简化为集中质量梁单元的解析公式能够在工程允许的误差范围内描述转体结构以指定振型振动时振动加速度与墩底弯矩的关系。

（3）基于2阶振型的峰值按绝对值叠加的假定，给出了桥梁平转过程振动加速度安全限值的推荐计算公式，可为同类工程的施工监控提供参考。但式（35）中2阶非对称振型对墩底弯矩的贡献比值还得依照以往的经验取值，其取值规律还有待进一步研究。

参考文献：

［1］张文学，黄荐，王秀平.连续梁桥平转施工过程稳定影响因素分析［J］.石家庄铁道大学学报：自然科学版，2012，25（4）：30－33.ZHANG Wenxue，HUANG Jian，WANG Xiuping.Analysis of Influencing Factors of Continuous Box－girder Bridge in the Process of Horizontal Rotation［J］.Journal of Shijiazhuang TieDao University：Natural Science，2012，25（4）：30－33.

［2］张文学，李增银，王秀平.平转速度和环境风速对临时固接结构受力影响分析［J］.公路，2013，58（3）：110－112.ZHANG Wenxue，LI Zengyin，WANG Xiuping.Analysis of the Influence of Horizontal Rotary Speed and Wind Speed to Temporary Fixing Structure in the Process of Flat Rotation［J］.Highway，2013，58（3）：110－112.

［3］韩艳，陈政清，刘光栋.双肢薄壁墩连续刚构桥平衡悬臂施工阶段的三维风效应研究［J］.工程力学，2008，25（10）：141－149.HAN Yan，CHEN Zhengqing，LIU Guangdong.Wind Loads and Effects of Rigid Frame Bridges with Twin－legged High Piers at Balanced Cantilevererection Stages［J］.Engineering Mechanics，2008，25（10）：141－149.

［4］余常俊，周勇军，刘建明，等.客运专线上跨既有繁忙干线铁路转体法施工监控技术［J］.铁道标准设计，2010，54（5）：68－71.YU Changjun，ZHOU yongjun，LIU jianming，et al.Flat Rotary Construction Monitoring Technology of Passenger Dedicated Line Bridge over Existing Busy Railway［J］.Railway Standard Design，2010，54（5）：68－71.

［5］黄先国.大西客专跨铁路连续梁桥转体施工监控技术［J］.国防交通工程与技术，2013，11（3）：45－48.HUANG Xianguo.Monitoring Techniques for the Rotating Construction of the Continuous Beam Railway Bridge of the Da－Xi Passengers－oriented Railway［J］.Traffic Engineering and Technology for National Defence，2013，11（3）：45－48.

［6］张文学，李建中，苏木标.轻型铁路桥墩横向振动问题研究［J］.工程力学，2006，23（8）：122－126，154.ZHANG Wenxue，LI Jianzhong，SU Mubiao.Transverse Vibration of Lightweight Railway－bridge pier［J］.Engineering Mechanics，2006，23（8）：122－126，154.

［7］苏木标，李建中，邹振祝.铁路简支梁桥竖向共振影响因素的分析［J］.工程力学，2004，20（4）：60－66.SU Mubiao，LI Jianzhong，ZOU Zhenzhu.Analysis of the Factors Influencing Vertical Resonance of Simply Supported Railway Girders［J］.Engineering Mechanics，2004，20（4）：60－66.

［8］BANERJEE S，CHI C，SHINOZUKA M.Kalman Filter－Based Identification of Bridge Fragility Parameters［C］／／ASCE.Proceeding of the 2011Structure Congress.Las Vegas，Nevada，USA：Structures Congress，2011：2 240－2 250.

［9］FENG M Q，KIM D K，YI J H，et al.Baseline Models for Bridge Performance Monitoring［J］.Journal of Engineering Mechanics，2004，130（5）：562－569.

［10］TRAVIS T，MARVIN W H，PAUL J B，et al.Structural Health Monitoring of the Cherry Hill Bridge［C］／／ASCE.Alexander：American Society of Civil Engineers，2006：1－8.

［11］秦浩，廖海黎，李明水.变截面连续钢箱梁桥典型施工阶段涡激振动［J］.西南交通大学学报，2014，49（5）：760－765.QIN Hao，LIAO Haili，LI Mingshui.Vortex－induced Vibration of Continuous Steel Box－girder Bridge with Variable Cross－sections at Typical Erection Stages［J］.Journal of Southwest Jiaotong University，2014，49（5）：760－765.

［12］刘健新，贾宁.悬索桥施工猫道的振动控制［J］.长安大学学报：自然科学版，2006，26（4）：54－57.LIU Jianxin，JIA Ning.Vibration Control of Catwalks for Suspension Bridges［J］.Journal of Changan University：Natural Science Edition，2006，26（4）：54－57.

［13］文永奎，孙利民.大跨度斜拉桥钢塔施工阶段振动控制［J］.同济大学学报：自然 科学版，2006，34（9）：1 152－1 158.WEN Yongkui，SUN Limin.Vibration Control of Steel Tower of Large Span Cable－stayed Bridge under Construction［J］.Journal of Tongji university：Natural Science，2006，34（9）：1 152－1 158.

［14］魏志刚，葛耀君，杨詠昕.大跨悬索桥对称和非对称架梁施工颤振稳定性研究［J］.土木工程学报，2008，41（6）：75－79.WEI Zhigang，GE Yaojun，YANG Yongxin.Study of Flutter Stability of Long－span Suspension Bridges with Symmetric and Non－symmetric Erection Approaches［J］.China Civil Engineering Journal，2008，41（6）：75－79.

［15］文永奎，孙利民.大跨度斜拉桥钢塔施工阶段制振用TMD、TLD装置及其性能试验［J］.地震工程与工程振动，2008，28（3）：157－164.WEN Yongkui，SUN Limin.TMD，TLD and Performance Tests for Vibration Control of Steel Tower of Large Span Cable－stayed Bridge During Construction［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（3）：157－164.

［16］徐刚，王靖夫，任文敏，等.施工中大桥桥塔的TMD减振研究［J］.工程力学，2003，20（6）：106－110.XU Gang，WANG Jingfu，REN Wenmin，et al.Reduction of Vibration During Construction of Bridge Towers by TMD［J］.Engineering Mechanics，2003，20（6）：106－110.

［17］李枝军，韩晓林，李爱群，等.悬索桥桥塔挂缆前后动态特性分析与测试［J］.中国公路学报，2007，20（5）：54－58.LI Zhijun，HAN Xiaolin，LI Aiqun，et al.Dynamic Analysis and Test of Bridge Tower of Suspension Bridge before and after Cable Installed［J］.China Journal of Highway and Transport，2007，20（5）：54－58.

［18］CLOUGH R，PENZIEN J.Dynamics of Structures［M］.Berkeley，California：Computers and Structures Inc，2003：377－386.

［19］铁道部经济规划研究院.通桥（2005）2368Ⅲ－ⅴ时速350公里客运专线铁路无碴轨道现浇预应力混凝土连续梁（双线）［Z］.北京：中国铁道出版社，2005.

［20］中华人民共和国铁道部.TB 10002.3—2005铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.北京：中国铁道出版社，2005.

［21］中华人民共和国铁道部.TB 10002.1—2005铁路桥涵设计基本规范［S］.北京：中国铁道出版社，2005.