不识图形真面目只缘身在此图中
2016-05-15浙江省宁波市北仑中学毛浙东
☉浙江省宁波市北仑中学毛浙东
不识图形真面目只缘身在此图中
☉浙江省宁波市北仑中学毛浙东
书有书胆,戏有戏核,数学老师给学生讲题,好比是说书唱戏,也要牢牢把握题目的核心——题眼.但是很多数学问题都被“包装”过,学生往往会被问题的表象所迷惑,无法看清其本来面目.比如在学习立体几何时,学生就常有“不识图形真面目”的困惑.笔者现以自己的一堂立体几何复习课的教学设计为例,来谈谈寻找题眼的常见方法,希望能抛砖引玉.
一、教学设计
1.在图形翻折中寻找题眼
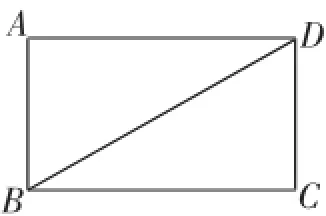
图1
A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
分析:容易判断选项A是错误的.对于选项B,我们发现直线AB与直线CD是异面直线,要判断它们在运动时是否会垂直是比较困难的,但注意到直线CD和直线AB是平行的,因此B选项可被翻译成:“如图2,把直角△ABD绕着BD翻折成△A′BD,请判断是否存在某个位置,使直线A′B与直线AB垂直?”在这个翻折过程中,我们发现线段AB“扫”出了一个圆锥的侧面,如图3所示.

图2
显然直线AB与直线A′B是这个圆锥的两条母线,在直角三角形ABD中,AB=1,AD=,故∠ABD>45°,因此圆锥的顶角∠ABE>90°,故在运动时,直线AB与直线AB′是有可能垂直的,故选项B正确.
对于选项C,我们发现由于此时新圆锥的顶角∠ADE<90°,如图4所示,故在运动时,直线AD与直线A′D不可能垂直,则选项C错误.
容易判断选项D也错误,因此本题答案为B.
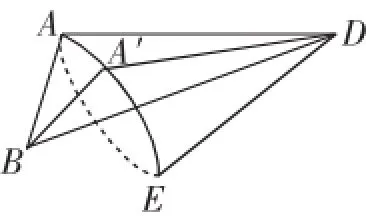
图4
点评:此题解法颇多,但笔者认为最优美,也是最本质的解法就是寻找此题的“题眼”.去掉包装后,我们发现本题的的翻折问题,看清了这一点,一切都变得明朗起来了.
2.在图形旋转中寻找题眼
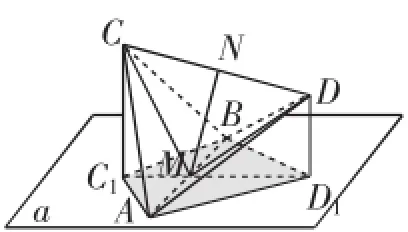
图6
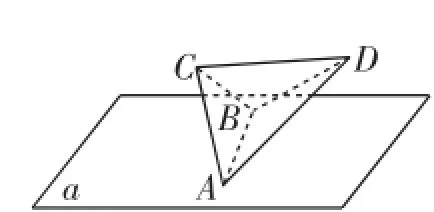
图5
分析:本题是个立体图形的旋转问题,如图6,我们发现当四面体旋转时,线段AB的长度保持不变,射影面积的变化取决于线段C1D1长度的变化,取线段AB的中点M,于是原题就退化成下题:在直角△CDM中,CM=1,,当△CDM绕着点M在垂直于α的平面内旋转时,△CDM在平面α内的射影线段长度的取值范围是多少?
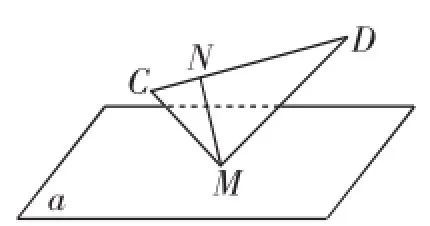
图7
如图7,过M作直线CD的垂线MN,垂足为N,当△CDM旋转时,容易发现:当CD与平面α平行时,射影线长度达到最大值影线长度达到最小射影线C1D1长度的取值此原四面体的射影面积为S=
点评:本题将立体问题平面化后,我们找到了这道题的题眼,其实质仍是一个棱长分别为1,的直角三角形的旋转问题,正是这个关键三角形的变化,决定了整个四面体在平面α内射影面积的变化.
3.在图形滑动中寻找题眼
例3已知直线l⊥α,正方体ABCD-A1B1C1D1棱长为1,若该正方体在空间符合下列条件:(1)A∈l,(2)C∈α,则O,C1两点间距离的最大值为_______.
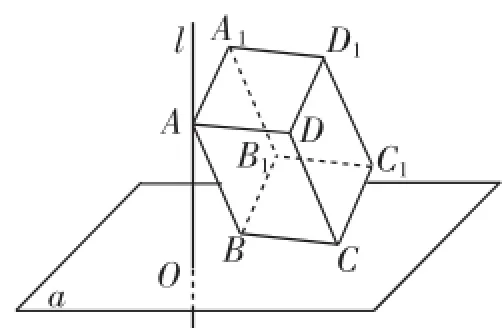
图8

图9
分析:在正方体运动时,我们发现A、C两个点在滑动,它们是两个关键点,而结论要求O,C1两点间的距离,因此O和C1也是关键点,而其他的点则无关紧要,因此本题可以退化成下题:已知直线l⊥α,在直角△ACC1中,CC1=1,AC=2%■,AC1=3%■,若该直角三角形在空间符合下列条件:(1)A∈l,(2)C∈α,则O,C1两点间距离的最大值为多少?
如图11,我们取线段AC的中点M,显然线段OM的长度保持不变,始终为AC长的一半(直角三角形斜边的中线为斜边长的一半),会变.由勾股定理可算得其长度为示.回到原题,我们知道所求距离
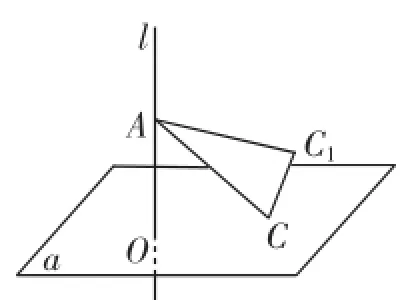
图10

图11

图12
点评:本题的题眼是一个棱长分别为1,2%■,3%■的直角三角形的滑动问题,我们之所以一开始难以看清其庐山真面目,就是因为它藏身于正方体中,褪去正方体这件外衣,答案自然就水落石出了.
二、几点思考
1.三道例题,一个模型
心理学研究表明,教师课堂上讲的题目跳跃度越大,特别是所讲的几个例题之间毫无关联,学生越容易产生疲劳,学习效率就会降低.反之,教师若给学生呈现的题目环环相扣,在学生的最近发展区对知识进行延伸,学生听起来就轻松,并理解得更深刻.众所周知,知识在我们大脑的建构是系统化的,而不系统的知识是不牢固的.
在本课中,教师给出了三道例题,系统地把“翻折、旋转、滑动”三种题型呈现在学生面前,而且巧合的是,三道题殊途同归,最终都化归为同一个模型,即一个棱长分别为1,的直角三角形的运动问题.整堂课下来,学生听得轻松,偶尔还发出惊叹声,但细细回味,又发现巧合中蕴藏着必然,不禁露出会心一笑.
2.三道例题,一种方法
本堂课教师给学生呈现了三道不同的题目,但是传授的方法却是如出一辙——寻找题眼.在立体几何问题中,题目的关键信息往往会藏身于复杂的图形中,如何将它们提炼出来就成为解题的关键.其实,无论是翻折、旋转还是滑动问题,寻找题眼最有效的方式就是努力寻找运动中的关键图形,从而使问题成功获解.
当然解决本课中的三道例题还有其他的思路,但教师没有将这些方法选入教学设计中,这样“罢黜百家、独尊儒术”的做法既是为了突出重点,也是为了让学生学会更本质地看问题.我们不排斥学生在课堂上用其他方法解决这些问题,但是教师应当鲜明地亮出自己的观点,因为能用同一种方法解决不同问题的方法,才能叫做通性通法.
3.三道例题,一个目标
张奠宙教授曾说:我们应启发学生欣赏数学的真、善、美.教师给学生传授正确的知识,就是求真;教给学生行之有效的解题的好方法,那是求善;带着学生一起欣赏数学,则是求美.在本课中,我们看到了数学思维的简洁美,图形本身的对称美,数学形式的统一美,表征和内涵的和谐美.教师不但自身要学会发现数学美,还有学会传播数学美.因为我们有一个共同的目标,让我们的学生也学会欣赏数学,并快乐地研究数学.
1.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
2.教育测量学[M].北京:人民教育出版社,2007.
3.张奠宙.数学教育随想集[M].上海:华东师范大学出版社,2013.
4.毛浙东.谈谈高三复习课例题的选择——解析一堂圆锥曲线最值的复习课[J].中学数学(上),2009(12).
5.毛浙东.巧用平面解析法破解立体几何题[J].中学数学研究,2011(3).
6.毛浙东.它山之石,可以攻玉——谈数学课堂融入故事的艺术[J].中学数学(上),2015(6).G
