变式教学在初中数学中的应用及实证研究

曹翠娟

什么是变式教学？顾明远的解释是：“变式教学是一种在教学中能够使得学生确切地掌握概念的重要方式.”那么变式教学如何在初中数学教学中应用呢？本文就该话题谈几点看法，以期有助于初中数学课堂教学高效发展.

一、变式教学在初中数学教学中的价值研究

1.变式教学的内涵

变式就是找到可以类比和迁移的内容，促进学生在问题解决中强化原有的认知，变式的过程是类比推理和思维方法迁移的过程.类比推理是以两个具有部分相同属性的对象为研究基础，通过对两个对象间相同属性的研究，并对其它相同属性进行推理，从而对新的概念能够有更深刻的认识和理解.变式教学是初中数学中比较有效的教学方法，利用变式教学能够提高学生的思维能力和创造力，激发学生的学习灵感和学习兴趣.

2.变式教学的教学价值

在初中数学教学中应用变式教学，能够帮助学生进行预习、新知识学习和复习，提高学生的学习技能，建立知识间的联系性.同时还能够激发学生的创新思维，有利于学生对复杂、繁琐数学知识的整理和学习.变式教学在初中数学教学，尤其是几何教学中应用是非常有价值的，初中阶段的几何变换本身就具有变式的味道，几何变换是按照相应的规律或者是法则，使其变化成另外一种图形的形式.通常情况下，较为常见的几何变化中包括了相似变换以及全等变化两种，其中相似变换会保证图像在其变化过程中形状不会发生改变，其他方面均可发生变化，如，图形方向、图形大小、图形位置等，因此它的应用范围相对较大.而全等变换则可以对点、线、角等进行变换位置，图形的大小是不能被改变的.在初中数学教学中利用变式教学，教师可以将结构繁琐的知识进行类比、梳理，通过知识和生活实例间的类比能够帮助学生缩小教学内容与生活实际的距离，降低数学知识的难度，激发学生的学习兴趣，提高学生举一反三的能力.

3.变式训练有助于学生形成良好的数学思维

初中数学在抽象性和严谨性上要高于小学数学很多.而初中生的思维模式还以形象思维为主，抽象思维和逻辑思维还处于发展阶段，所以在初中数学的学习中，学生仍需要通过多个具体的实例来对知识进行了解和掌握.变式训练能够帮助学生多次将抽象知识与具体实例相结合，帮助学生形成良好的数学思维.同时，从初中数学知识的结构上看，各知识点都存在一定的联系性，这也为变式教学在初中数学中的应用提供了一定的基础.

二、变式教学的实证性研究

变式教学在初中数学教学中应用很广，不仅仅在习题课教学中有所应用，在概念课教学中也有应用.下面笔者以初中几何概念教学为例就其实证性进行分析.

1.几何概念的特点分析

研究初中几何概念的特点是实现有效变式的前提，纵观当前初中数学几何教材，涉及到的概念具有如下几个特点：（1）逻辑判断性；（2）实践性；（3）直观性；（4）系统性.

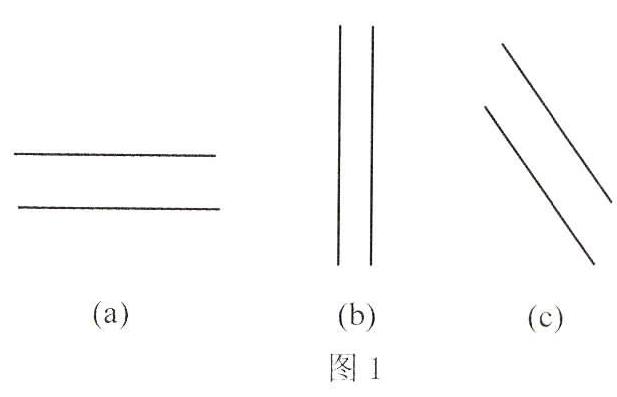
例如，平行的概念，学生生活实践中存在，课堂上也随手可得，如书的上下边，桌子的两条边等等，但是教学中应该从学生的生活实践中较为熟悉的并存在记忆中的平行（如图1中的a、b）出发进行图形变式（如图1中的c），让学生通过概念变式对平行有更深刻的理解.

2.几何概念的变式教学实践

下面以《三角形的中线》教学为例，就如何进行变式教学进行分析.

（1）画多条三角形的中线，引入中线的概念

对于三角形中线的概念，在教学过程中可以用几何画板画一个三角形，然后画出这个三角形的三条中线，引入中线的概念.

（2）图形变式，引导学生在辨析中理解概念

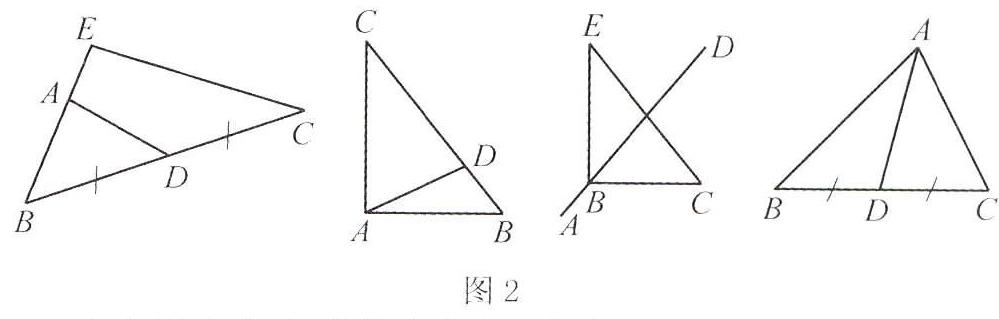
在建立概念后，为了进一步深化学生对概念的理解，提供如图2所示的多组变式图形，要求学生对中线进行辨析和判断，继而深化对概念定义和中线的性质的理解.

（3）语言变式，多维度表征几何概念

一个具体的概念可以从多个维度进行表征，不仅仅只有语言文字表达，还可以用公式、符号，以及图形表征，尤其是几何概念的教学，我们在变式教学中应该引导学生从多个维度对概念进行分析和理解.

（4）变式训练，找到共性

设置例题，分别呈现出锐角三角形、直角三角形和钝角三角形，要求学生分别画出每一个三角形的三条中线，这一个环节是对前面概念的有一次强化，而且在多个三角形中进行画中线，接着观察到无论是哪一种三角形，都有一个共性：“三条中线交于三角形内的一点”.在变式中发现中线的共性，作图的过程是学生将前面学习到的概念进行应用的过程，在作图的过程中实现认知的进一步有效延展，思维和能力、情感也随之有所发展.

教学反思 在中线这个概念的教学过程中，借助于图形的变式完成了概念的导入，让基本概念进入学生的大脑留下浅浅的痕迹；然后再一次借助于图形变式让学生对“中线”进行辨析，学生在辨析的过程中运用概念摒弃错误的过程是深化对概念理解的过程；接着又引导学生从多个维度对中线的概念进行表征形式的变化，这一过程是学生提取概念中的重要信息和关键词的过程，从多个维度对概念进行理解，概念在学生头脑中基本有了完整的形态，沉淀下来；最后再要求学生自主画图实践，实现在具体的问题情景中应用中线的概念，实现对概念本质的理解，促进知识的内化.