勾股定理在“数形结合”中的巧妙运用

黄郑

【摘 要】勾股定理是几何中一个重要的定理，它揭示了直角三角形三条边之间的数量关系，它可以解决许多直角三角形中的计算问题，是解直角三角形的主要依据之一。教师在授课中应选取典型例题进行讲解，灌输“数形结合”的思想，提高学生对定理的理解和综合运用。

【关键词】勾股定理；直角三角形三边数量关系；“数形结合”

勾股定理是描述直角三角形三边特殊关系的重要定理，其内容是在任意直角三角形中，两条直角边的平方和等于斜边的平方。在研究与直角三角形三条边长有关的计算问题时，勾股定理都有着重要的应用。教师在讲述《勾股定理》的内容时，要精选例题，结合实际图形分析讲解，培养学生识图分析能力和“数形结合”的数学思想，提升综合应用能力。

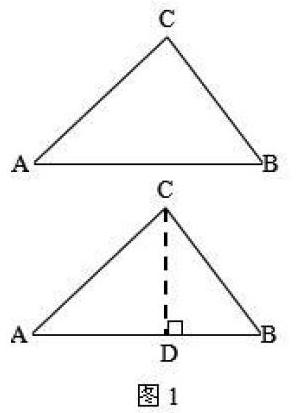
有这样一道题目：如图，在△ABC中，BC=4，AC=5，AB=7，求△ABC的面积。

这道题目不能直接用三角形的面积公式来求解，而是要运用与“勾股定理”相关的知识以及添加辅助线的方法进行解答。其解决思路是：过点C作AB边上的垂线，垂足为点D（如图1所示），于是就把原三角形分成两个直角三角形，分别是Rt△ACD和Rt△BCD，它们有公共的直角边CD，斜边分别是AC和BC，运用勾股定理可以得出：

AD2+CD2=AC2，BD2+CD2=BC2，所以CD2=AC2-AD2，CD2=BC2-BD2，于是得出AC2-AD2=BC2-BD2；设AD的长为x，则BD的长为7-x，而AC=5，BC=4，代入上述的结论中可得出方程：52-x2=42-（7-x）2，解方程得出x=，再在Rt△ACD中运用“勾股定理”就可求出CD的长（也可在Rt△BCD中运用“勾股定理”求出CD的长），这样在△ABC中，应用三角形的面积公式就可求出原三角形的面积了。

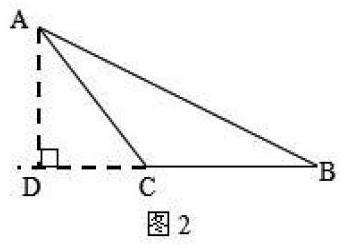
此题也可以作AC或BC边上的高，方法与上述解法类似。在讲解过程中，教师要引导学生分析本题图形存在的不同情况，培养学生“分类讨论”的思想，即当三角形变为钝角三角形时，如图2，若作BC边上的高AD，此时形成的两个直角三角形是Rt△ACD和Rt△ABD，它们公共的直角边是AD，斜边分别是AC和AB，运用勾股定理并转换之后得出的等式是AC2-CD2=AB2-BD2，此时可设CD的长为x，则BD的长为x+4，于是得出方程52-x2=72-（x+4）2，解方程得出x=1，再在Rt△ACD或Rt△ABD中，运用勾股定理求出AD的长，再求原三角形的面积。

通过上述问题的分析与解答，不难看出“勾股定理”的运用与方程有着十分紧密的联系，很多几何图形的计算问题都可以通过设未知数，建立方程来求解，因此，教师在讲解勾股定理在“数形结合”中的运用时还要有意识地向学生灌输“数学建模”的思想。

教材中有一道例题：如图，一架长2.6米的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4米；如果梯子的顶端A沿墙下滑0.5米，那么梯子的底端B也外移0.5米吗？

很多学生会误认为A点下滑的长度与B点外移的长度是相等的，这是认识上的误区。本题的关键是要通过计算求出线段BD的长度，与线段AC的长度比较才能得出结论；而要求线段BD的长度，就要先运用勾股定理求出线段OD、OB的长度。因此，在指导学生识图分析时，要理清条件之间的关系和求解的步骤，要让学生明确题目的解答思路，才能取得较好的学习效果。

本题的解答思路是：先在Rt△ABO中运用勾股定理直接求出线段OB的长度；由梯子的顶端A沿墙下滑0.5米，求出线段CO的长；再在Rt△CDO中运用勾股定理求出线段OD的长度，最后用OD减去OB就求出BD的长，再与AC的长比较，得出问题的答案。

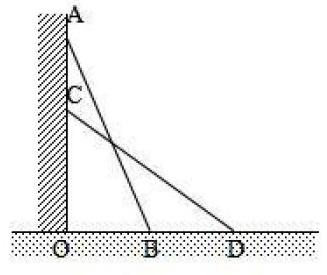
在教材中有一道题目：如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上；求证：AE2+AD2=2AC2。

这道题目要求证的结论中的三条线段AE、AD、AC没有直接的关系，因此要通过（相等）线段的转换，在同一个直角三角形中运用勾股定理才能找到关系，得出结论。其解题思路是：有条件可知AC=BC，所以2AC2可以转换为AC2+BC2，而在Rt△ACB中AC2+BC2=AB2，所以2AC2=AB2，这里用到了数学中的“转换思想”；而本题的难点在于要连接BD，如图3所示，于是运用已知条件可以得出一组全等的三角形△ACE和△BCD，从而就可以把线段AE转换为线段BD，同时得出∠BDC=45°，因为∠ADC也等于45°，所以∠ADB=90°，这样AE、AD两条线段就转换为直角三角形ADB的两条直角边BD和AD，于是运用勾股定理可得出BD2+AD2=AB2，所以AE2+AD2=BD2+AD2=AB2=2AC2。

这道题目的难易度属于中等偏难的程度，教师在授课过程中要注重引导学生结合图形去观察、分析和猜想，理清思路，发现题目中蕴含的数学思想和方法，以及条件和所求问题之间的相互联系，提升学生对“数形结合”思想的理解和应用。

“数形结合”是数学中常用的、重要的思想方法之一，华罗庚教授就曾指出：“数缺形时少知觉，形少数时难入微”，勾股定理在“数形结合”中的运用只是“数形结合”这一思想方法的一个方面的体现。我们在研究几何图形中的数量关系时，一定要结合图形直观地去探索和研究，不能空洞地思考；反之，几何图形中又蕴含了与其紧密联系的数量关系，很多图形的问题，往往又要用到代数的相关知识去求解。因此，在教学过程中，要辩证地看待“数”和“形”之间的关系，把二者有机地结合起来，帮助学生正确养成“数形结合”的数学思想，提升学生的识图分析能力、逻辑推理能力和综合解题能力。

【参考文献】

[1]摘自《人教版数学八年级下册教师教学用书》.中《勾股定理》.一章的教材分析