Active disturbance rejection control:between the formulation in time and the understanding in frequency

Qing ZHENG ,Zhiqiang GAO

1.Department of Electrical and Computer Engineering,Gannon University,Erie,PA 16541,U.S.A.;

2.Center for Advanced Control Technologies,Department of Electrical and Computer Engineering,Cleveland State University,Cleveland,OH 44115,U.S.A.

1 Introduction

As the object to be controlled,physical plants in real world are not just nonlinear and time-varying but also highly uncertain.As the well-known control theorist Roger Brockett puts it:“If there is no uncertainty in the system,the control,or the environment,feedback control is largely unnecessary”[1].For much of its history,however,mathematical control theory has been developed largely based on the premise that a physical plant behaves rather closely as its mathematical model describes.Serving as the point of departure in control system design,this assumption does not reflect either the necessity of feedback control,nor the physical reality.The premise of model has stimulated in the last few decades lively debates and rapid new developments,such as those under the umbrella of robust,adaptive,and nonlinearcontrol.Butthe dependence on the model proves difficultto shake loose even though the engineering practice of automatic control has taught us that PID,with over a hundred years of history,is still the king,and that engineers by and large have little use of design techniques premised on a detailed mathematical model of the physical process to be controlled.

The practicality of a model-based design can be problematic in two regards:1)it could be rather expensive to obtain a detailed mathematical model;2)even if such a model is obtained,the uncertainties in the process,particularly the changes in the system dynamics,could easily render such model obsolete during operation.Such problems prove to be hard to overcome even with the most advanced techniques such as those known as robustcontrol,where the controlleris made tolerantofuncertainties to some degree but still requires nonetheless a fairly detailed and accurate mathematical model of the plant.For example,the robust control design methodology based on the small gain theorem does allow a small amount of uncertainties in plant dynamics,but not anywhere near the magnitude often encountered in practice.The problem of controlling a process of a large amount of dynamic uncertainties remains unsolved until a new paradigm,namely active disturbance rejection control(ADRC),came to the scence.

The ADRC resonates with practical minded researchers from the very beginning when Han argued that there must be a way to control a process independent of its mathematical model.The framework and conceptual underpining gradually took shape in the span of two decades between 1989 and 2009,as explained in[2–11].They fundamentally differ from other disturbance-centric design methods in the very concept of disturbance,which has been widely taken as forces external to the process to be controlled.Han inherited the notion of disturbance from H.S.Tsien that is more general and inclusive,including both the internal as well as the external disturbance.Tsien coined the term internal disturbance but Han took it to the next level,namely the total disturbance,which could very well be a function of the states of the process.In doing so,Han found a way to deal with the problem of large amount of dynamic uncertainties and to escape from the suffercating hold of the model-based design methodology.

The solution turns out to be a simple one:treat the process dynamics and external disturbance alike;lump them into a whole called the total disturbance;and then find a way to estimate and cancelit,reducing the process dynamics to an ideal,disturbance-free form.It is therefore obvious that whole enterprise comes down to the question of if such disturbance can be indeed estimated and cancelled.To this end Han left us with the extended state observer(ESO)[4],in a manner of experimental science:daring hypothesis followed by two decades of meticulously constructed tests,both in simulation and experimentations.In fact,Han pioneered the method of investigation in search of effective control mechanisms using computer simulation as the main tool[11].

To be sure,disturbance estimation and cancellation has been studied by many researchers over the years and many solutions have been offered,such as the unknown input observer(UIO)[12–19],the disturbance observer(DOB)[20–27],and the perturbation observer(POB)[28–31].Two recent surveys can be found in[32,33].The key difference from ADRC is that they are intended to compliment the existing model-based paradigm rather than replacing with a new one.The new ADRC paradigm started slowly but picked up speed recently,largely propelled by its large scale adoption as a viable industrial solution,threatening the dominance of the PID solution.What was for a long time an experimental solution all the sudden acquired the attention of researchers intending to grasp its stability properties.This paper summarizes some recent results in the analysis of linear ADRC(LADRC)and offers explanations in the frequency response language with which practicing engineers are familiar.

Ais Hurwitz for the αi,i=1,2,...,n+1,chosen above.

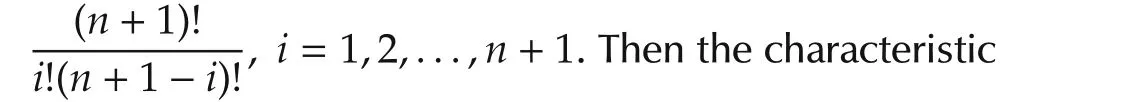
The paper is organized as follows.The time domain formulation of the ADRC is presented in Section 2.The engineering insight from frequency responses is discussed in Section 3.The time domain and frequency domain connection is given in Section 4.The time domain validation is shown in Section 5.The paper ends with a few concluding remarks in Section 6.

2 Time domain formulation of the ADRC

The ADRC was originally proposed as a combinatin of a tracking differentiator(TD)plus an ESO with a nonlinearform[3].The key ofthe ADRC is the ESO.In[41],the ADRC was proposed to be realized with a PD controller and a linear extended state oberser(LESO),formulating a LADRC.In this paper,the presented ADRC approach refers to LADRC.

伴随就业问题的凸显，大学生在就业中的焦虑问题越越来越普遍。就业焦虑按照在就业问题上的具体表现分为：冲动型（高焦虑阶段高效能）、无助型（低焦虑阶段、效能低）、稳健型（低焦虑阶段 高效能）、冷漠型（低焦虑阶段、低效能）

First the ESO design is presented.Consider a generally nonlinear time-varying dynamic system with singleinput,u,and single-outputy,

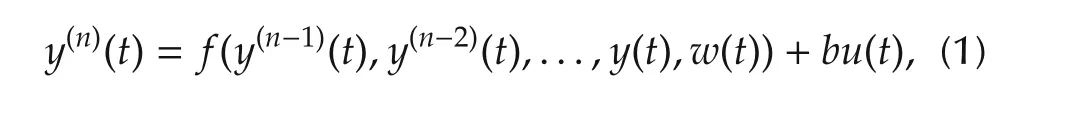
wherewis the external disturbance andbis a given constant.Heref(y(n-1)(t),y(n-2)(t),...,y(t),w(t)),or simply denoted asf,represents the nonlinear time-varying dynamics of the plant that is unknown.That is,for this plant,only the order and the parameterbare given.The ADRC is a unique method designed to tackle this problem.It is centered around estimation of,and compensation for,f.To this end,assumingfis differentiable and leth= ˙

f,(1)can be written in an augmented state space form

wherex=[x1x2···xn+1]T∈Rn+1,u∈R andy∈R are the state,input and output of the system,respectively.Any state observer of(2),will estimate the derivatives ofyandfsince the latter is now a state in the extended state model.Such observers are known as ESO.

本文试图从Github开源社区软件开发演进过程的数据入手，通过存储库数据挖掘的方法找到一种能够对开源软件的成功度进行客观量化度量的、简单易行的新方法，从而使能开源软件开发团队快速了解所开发软件的成功程度和团队状况，明确影响开源软件成功的关键因素，指导开源软件的领导者采取合适的行动.

综上所述，安列克联合缩宫素和益母草比单独缩宫素联合益母草预防前置胎盘产后出血的疗效好并且安全，值得临床推广。

Withuandyas inputs,the ESO of(2)is given as

⑥后期维护便利性。治理工程后期维护要方便简捷，工程不需要频繁维护，工程在遭到简单破坏后能完成自我修复。

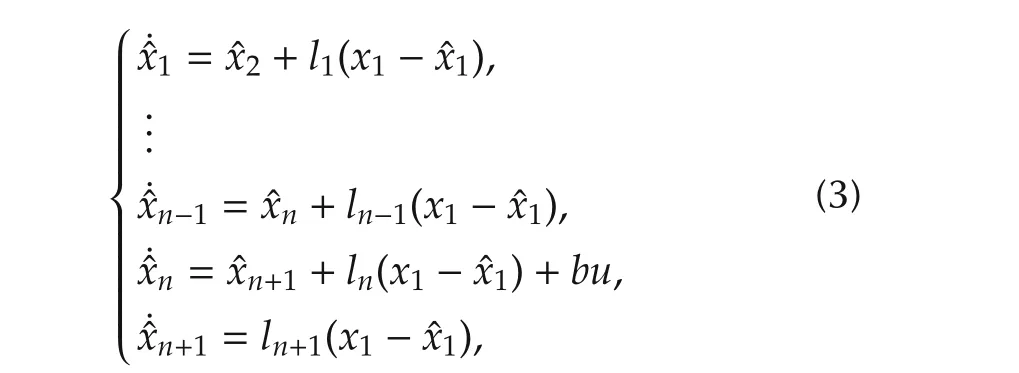
wherex=[x1x2···xn+1]T∈Rn+1,andli,i=1,2,...,n+1,are the observer gain parameters to be chosen.In particular,let us consider a special case where the gains are chosen as

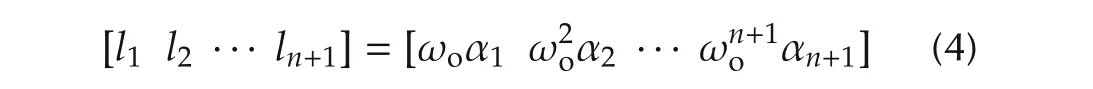
The first attempt at the rigorous study of stability of the ADRC solution can be found in[34],where,for the sake of ease,the nonlinear gain structure of the original ADRC is replaced with a linear one.For the first time the convergence of the ESO and the bound on the tracking error in the ADRC were established,which lent support to the engineering success ofthe ADRCand furtherstimulated research interests on the subject.The research has grown more intensely and fruitfully since then,as can be seen in the more recent publications in[35–40].But there is one nagging problem that refuses to go away:the more rigorous study of ADRC has done little to provide guidance to its engineering applications.This paper intends to address this issue,as one of the languages.In particular,we believe that the language of the time domain analysis based on solving differential equations must be intimately connected with the language of frequency responses with which engineers are familiar.This can be done,as shown earlier in[34],by solving the differential equation and examining the properties of the solutions directly,instead of using the Lyapunov type of methods that tend to be rather conservative and cubersome.

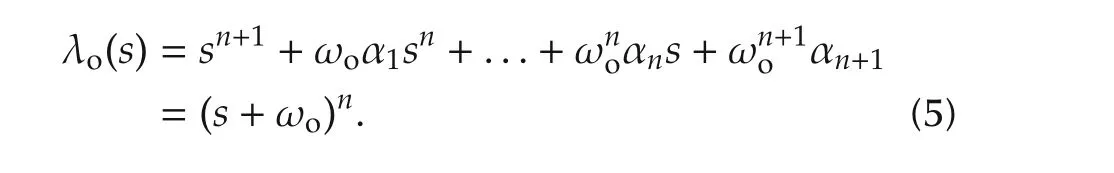
and ωo,the observer bandwidth,becomes the only tuning parameter of the observer.

When a system model is known,then with the given functionh,the ESO of(2)now takes the form of

兰江大桥高高地矗立着。蒋大伟把车开到路边，两人仰头看着大桥。桥上，车辆在不停地穿梭流动。蒋大伟低声地：这就是兰江大桥！郑馨默默看着大桥，没有说话。蒋大伟继续说道：我没说错吧，兰江大桥很有气势，很美。郑馨还是没说话，她打开车门，蒋大伟：就这么下车了，不想再说点什么吗？郑馨仍然没说话，蒋大伟急了：等等！临死之前，还有什么未了之事，或许我能再帮你个忙。郑馨皱紧眉头，像竭力想着什么。蒋大伟说：反正是快死的人了，没什么不好说的。郑馨想了想，咬牙切齿地：我想等陈晓来，让他看看我是怎么死的！

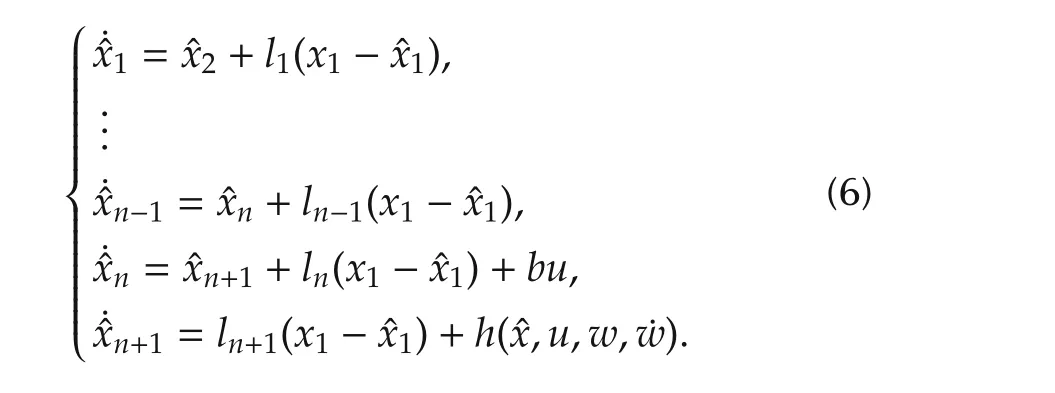
Assume that the control design objective is to make the outputofthe plantin(1)follow a given,bounded,reference signalr,whose derivatives,˙r,¨r,...,r(n),are also bounded.Let[r1r2...rnrn+1]T=[r˙r1···˙rn-1˙rn]T.Employing the ESO of(2)in the form of(3)or(6),the ADRC control law is given as

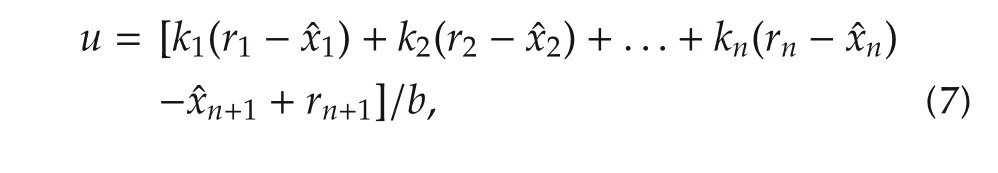
whereki,i=1,2,...,n,are the controller gain parameters selected to makesn+knsn-1+...+k1Hurwitz.The closed-loop system becomes

Note that with a well-designed ESO,the first term in the right hand side(RHS)of(8)is negligible and the rest of the terms in the RHS of(8)constitutes a generalized PD controller with a feedforward term.It generally works very well in applications but the issues to be addressed are:1)the stability of the closed-loop system(8);and 2)the bound of the tracking error.Note that the separation principal does not apply here because of the first term in the RHS of(8).

3 Engineering insight from frequency responses

Most of the development and analysis of the ADRC have only been shown in time domain.In[42],frequency-domain analysis of the ADRC is performed to quantify its performance and stability characteristics.In[43],it is shown that the amount of uncertainties can be reduced by way of active disturbance rejection,implemented in an inner loop to produce a well-behaved plant,which is then regulated by another controller in the outer loop.In[44],the ESO is brought into the frequency domain to show to what degree it forces the plant to behave like cascaded integrators and what can be done to improve the performance when the ESO is bandwidth limited.Some rigorous analysis for the frequency domain properties of ADRC has been given in[45].

3.1 Frequency response analysis

Consider a linear time-invariant second-order plant:

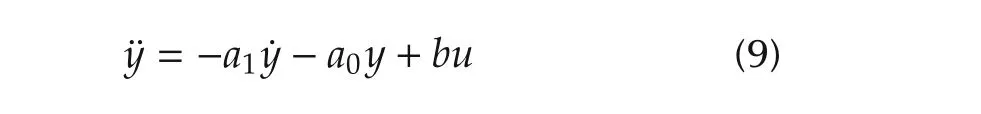
witha0anda1unknown,f=-a1˙y-a0yin this particular case.Since both the plant and the controller are linear,the robustness of the control system can be evaluated using frequency response.If ADRC indeed estimatesfand cancels it out,then we should see very little change in bandwidth and stability margins whena0anda1vary.

The Bode plots of the loop gain transfer function are shown in Fig.1.With ωc= ωo=100 rad/s,b=206.25,a1=3.085,anda0=[0 0.1 1 10 100],Fig.1(left)shows that,remarkably,gain margin,phase margin and cross-over frequency are almost immune to changes ina0.Similarly,with ωc= ωo=100 rad/s,b=206.25,a0=0,anda1=[0.1 1 3.085 10 100],Fig.1(right)demonstrates that gain margin,phase margin and crossover frequency are just as insensitive to changes ina1as to those ina0.

从对落实基础知识调查的问卷调查数据发现，有24.78%的学生需要老师对基础知识讲的更详细，这部分学生基础知识落实较差，需要另外采取措施去落实和巩固，不然没有扎实的基础知识的学生谈何提升能力，谈何培养学生的地理核心素养。针对学生反映的课前预习效果偏低的问题，可从教师和学生两方面共同解决。教师采取课堂检查和督促课后巩固相结合。

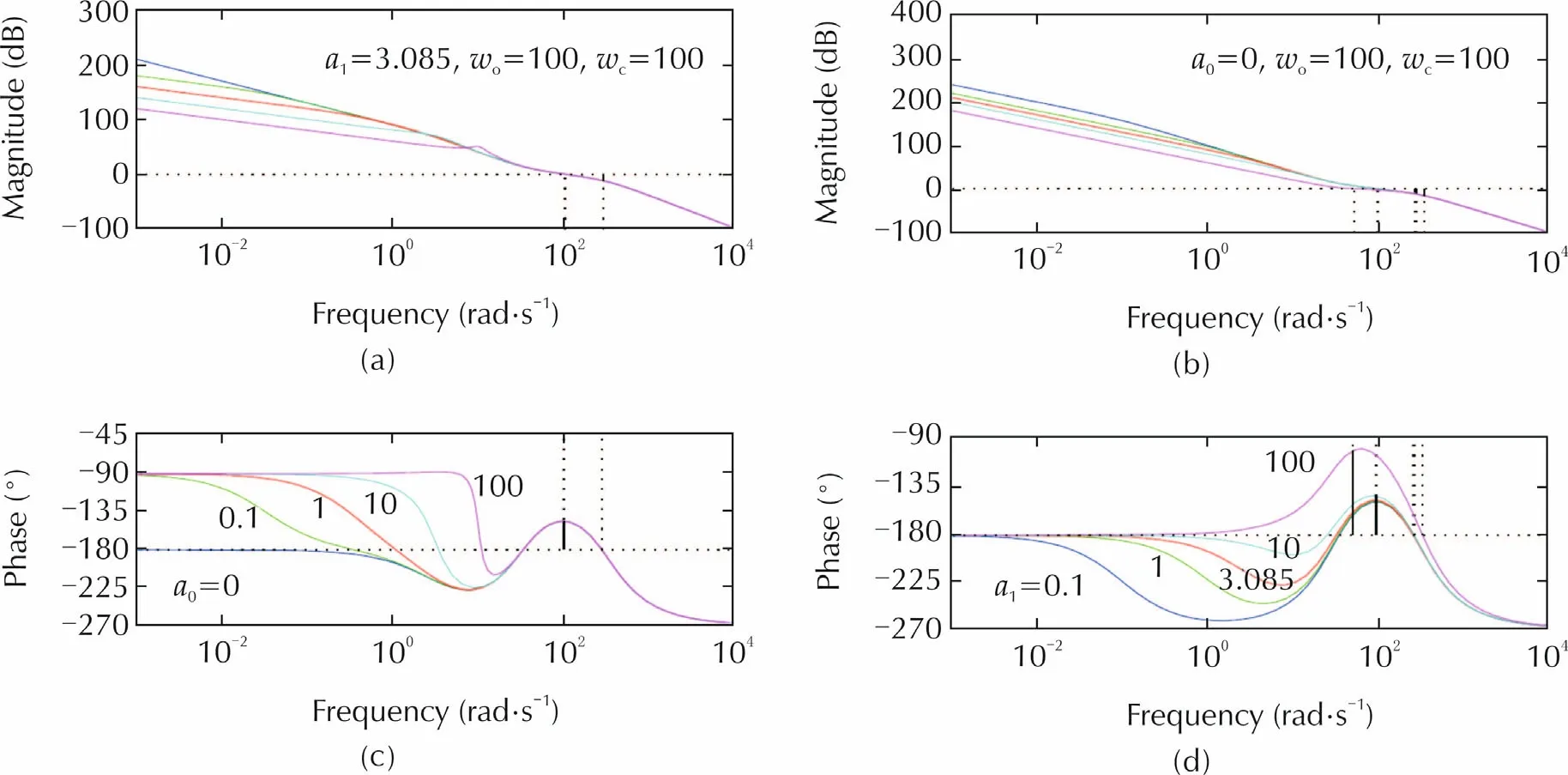
Fig.1 Loop gain Bode plots at different a0 and a1.(a)and(c):a0=0,0.1,1,10,100.(b)and(d):a1=0.1,1,3.085,10,100.

First,consider the ESO with the given model of the plant.Let˜xi=xi-xi,i=1,2,...,n+1.From(2)and(6),the observer estimation error for the system with a given model can be shown as

3.2 Uncertainty reduction through active disturbance rejection

The theme ofmodern controlis how to getaround the unknowns,i.e.,model uncertainties and disturbances,so that they do not degrade what is valued:stability and performance.In[43],it is demonstrated that the uncertainty stemming from both the external disturbance and the unknown internal dynamics,which is the subject of intense research efforts in the last few decades,can be greatly reduced through active disturbance rejection.Accordingly,it is demonstrated that control of uncertain system can be carried out in two steps:1)reducing the uncertain plant,via active disturbance rejection,to a class of cascaded integral plants;and 2)design the front end controller for these compensated plants.

得到老师的表扬后，越来越多的孩子开始帮助小鹏。一天，我看到教室地上有个塑料瓶和一张废纸片，就在我准备弯腰的一刹那，一个学生抢先一步捡走了塑料瓶，然后对着小鹏喊：“小鹏，给你一个塑料瓶。”而地上的纸片却一直无人问津。顿时，我眼前一亮：如果纸片也能像塑料瓶一样有人收集利用、变废为宝的话，那些躺在地上的废纸就不会无人理睬了，是不是也会像塑料瓶那样被孩子们抢着捡呢？

某高速公路设计速度为100km/h，路基宽度28m，路面结构形式为半刚性基层沥青路面，基层设计为34cm水泥稳定碎石，考虑到开放交通后，交通量较大，可能有大量重型运输车辆通行，研究决定在试验路使用异步连续摊铺技术进行半刚性基层施工，以提高基层整体性与承载能力，为该技术在全线展开打下基础。

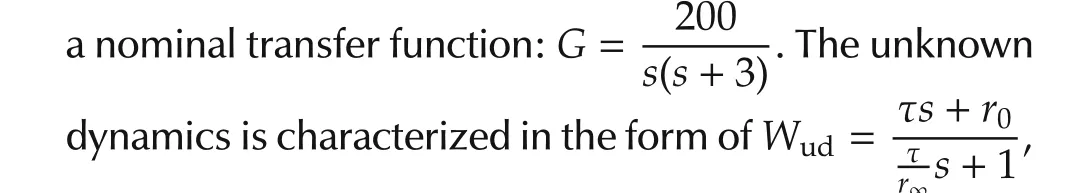
To demonstrate the effectiveness of the ESO in uncertainty reduction,consider a second order plant with wherer0is the modeling error in steady state,r∞is an uncertainty scalar at high frequency,and τ-1is the frequency at which the system is completely unknown.Herer0=1,τ-1=0.2π,andr∞=5.The perturbed plant is of the form:

If the ESO can fairly estimate the total disturbance,then the purtubed plant(10)can be reduced to¨y=u0.Bode plots of the transfer function for the plant¨y=u0fromu0toyare shown for different observer bandwidths in Fig.2.It demonstrates the amount of uncertainty reduction by the ESO.Clearly,the quality of uncertainty reduction is directly correlated to the bandwidth:the higher the ωo,the closer the compensated plant is to the ideal double integral plant.From Fig.2 it is concluded that the plant fromu0toyis reduced to a pure double integrator with very small error up to the frequency of 0.1ωo.That is,the control design problem is reduced to dealing with a pure double integral plant at or below the frequency of 0.1ωo.

走进柳州，郁郁葱葱的城市绿化和优美宜人的生态环境，映入眼帘。一如广西许多地方一样，山清水秀，鸟语花香。然而在保持这样的生态环境之下，柳州被冠以“西南工业重镇”的名号。工业化与生态环境建设，不可多见地在柳州和睦相处。

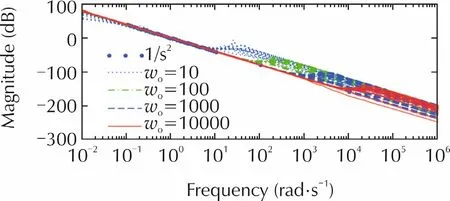
Fig.2 Magnitude plot of the compensated plant.

3.3 The enhanced ADRC design with a low observer bandwidth

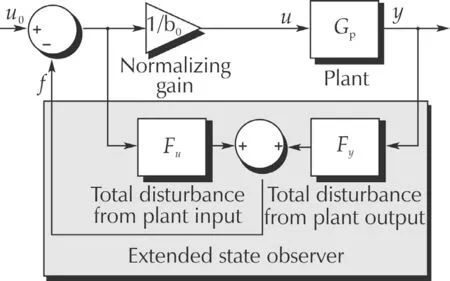
Fig.3 Single integral plant acting as double integral.

By assigning allpoles ofthe observertoωo,denoted as the observer bandwidth,the process of selecting gains in ESO becomes one of simply tuning ωo.The modified plant,i.e.,the transfer function fromu0toy,can be shown as

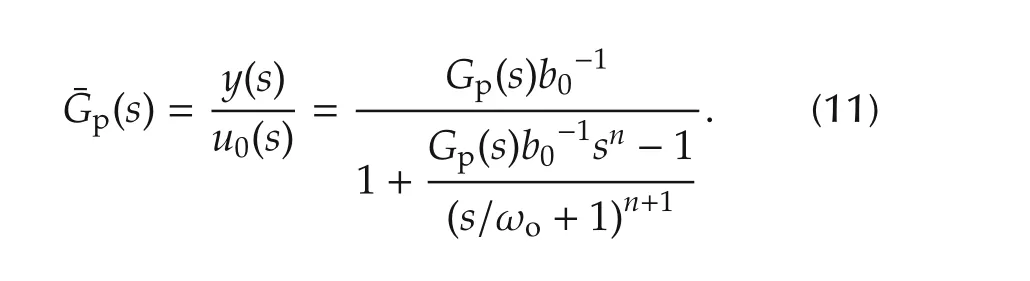
Note that the denominator contains a low-pass filter of ordern+1 with a corner frequency of ωo.If this is imagined as an ideal filter,where it acts as unity gain at and below the corner frequency but zero gain above it,the frequency response of(11)can be expressed as

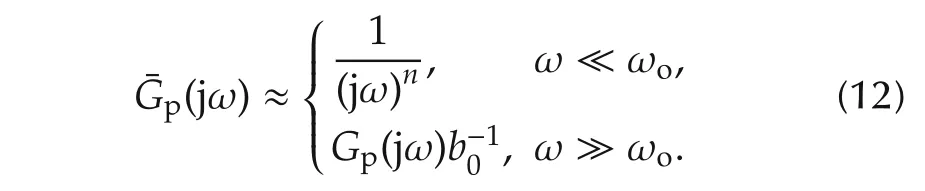
It can be seen from(12)that the modified plant acts as perfect integrators of ordernwithin the bandwidth of the observer.At high frequencies,it will instead follow the response of the plant.It can be assumed that if an infinite bandwidth could be selected in an ideal world without noise or sampling,then the plant would indeed act as a perfect integral of ordernregardless ofGp.By rearranging(11)as(13),the transition from the desired integral form at low frequency to the original plant at the high frequency can be captured by the transfer function of¯Gp(s)in the form of(13),where a low-pass filter shapes the plant into the integral form at low frequency and a high-pass filter shapes the plant at high frequency.

从表2可以看出，实验组学生在出科考核中的理论知识、操作技能、临床思维方面均优于对照组学生，由此得出结论，采用虚拟技术辅助教学模式的实验组教学效果明显优于采用传统教学方法的对照组。从表3 可以看出，在教学满意评价调查问卷中，实验组的各项满意度评价均高于对照组。

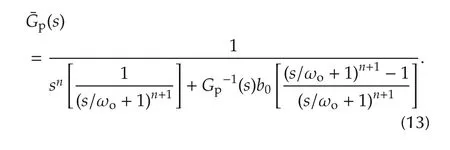
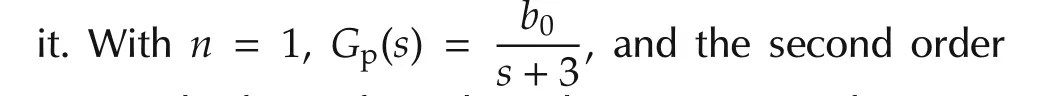
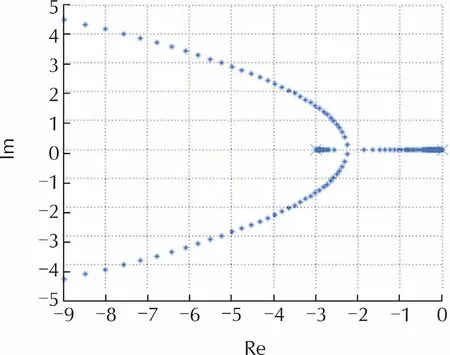
Fig.4 Closed-loop poles for the 1st order plant as ωo varies.

This pattern is the same for any stable first-order plant.By monitoring how the poles ofthe modified plant move,it can be better understood how ADRC forces the plant to behave like cascaded integrators.The information about the imperfection can be used in the control design to better accommodate the remaining dynamics beyond the cascaded integrators.

4 Time domain and frequency domain connection

In[41],the ESOand the associated controllerwere parameterized,thusly LESO and LADRC were formulated.In that paper,the observer bandwidth and controller bandwidth,which engineers are familiar with,were first connected to ESO and ADRC as the tuning paramters.The parameterization of ESO and ADRC makes the concept very easy to understand and implement by engineers,therefore widely used in practice[46–48].Critical to the connection between time domain formulation and frequency domain insights is established through the use of bandwidth in time domain analysis.

In many real world scenarios,the plant dynamics represented byfis mostly unknown.The ESO design for a system with dynamics largely unknown is shown below.

With the parameterized ADRC,the first attempt at the rigorous study of stability of the ADRC solution can be found in[34].For the first time the convergence of the ESO and the bound on the tracking error in the ADRC were established by solving differential equations.The detailed derivations are given in[49].

4.1 Convergence of the ESO error dynamics

The results show that the active disturbance rejection based control system possesses a level of robustness that is rarely seen.The bandwidth and stability margins,in particular,are kept almost unchanged as the plant parameters vary significantly.

加强学习提升素质。每月组织1-2次学习会，集中学习《中国共产党纪律处分条例》、《中国共产党问责条例》等党规党纪、中央最新精神以及业务工作知识，加强平时自学，注重理论联系实际，不断提升队伍素质、能力，夯实监督执纪工作基础。

此方法需要把各方面变动所形成的差距联系到一起，然后再逐一进行分析，整个过程的关键点在于需要确定“亏损边界点”，然后在对其展开工作，需要注意的是，动态上所出现的变动因素与单位的盈亏是存在一定关联的，而这对单位从经营决策中采取相应措施有很大的帮助。

The proof of this theorem has been given in[50].

When the plantdynamics is largely unknown,the ESO is designed as shown in(3).Consequently,the observer estimation error becomes

The proof of this theorem has been given in[49].

她爸爸是谁？大家不约而同地在心中画了个问号。马县长走到何副书记面前说：“老何，殊书是吴军同志的女儿，望你们在生活上多照顾点儿。”

In summary,when the plant model is given and used in the ESO,the dynamic system describing the ESO estimation error is asymptotically stable;and in the absence of such model,the ESO estimation error is bounded and its upper bound monotonously decreases with the observer bandwidth.The stability characteristics of the ADRC,where the ESO is employed,is presented next.

4.2 Stability characteristics of the ADR C

In[49],the stability characteristics of the ADRC are presented for both the cases of the plant model given and plant dynamics largely unknow.

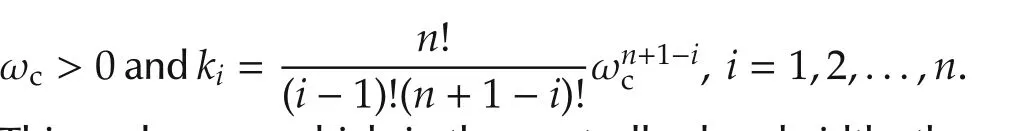
For the case of the plant model given,one has the following theorem.

Theorem 3Assumingh(x,u,w,˙w)is globally Lipschitz with respect tox,there exist constants ωo＞ 0 and ωc＞ 0,such that the closed-loop system(8)is asymptotically stable.

Now we consider the case that the plant dynamics is unknown and the ESO in the form of(3)is used instead.

The proofofTheorems 3 and 4 can be found in[49].In summary,with the given model of the plant,the closedloop system(8)is asymptotically stable;and with plant dynamics largely unknown,the tracking error and its up to(n-1)th order derivatives of the ADRC are bounded and their upper bounds monotonously decrease with the observer and controller bandwidths.

The above analyses show thatthe observerbandwidth and control loop bandwidth are associated in the time domain stability analysis with the upper bounds of the observer error and the tracking error,respectively.This makes such analysis relevant to the common design considerations and concerns shared by practicing engineers.

5 Time domain validation

With the convergence ofthe ESOand the ADRC established,a simulation study of nonlinear plant with partial model information is presented below.

Consider the following nonlinear system

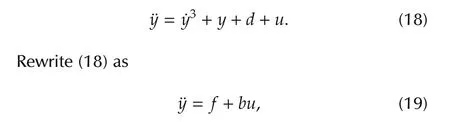
wherefrepresents the summation of the plant dynamics˙y3+yand the external disturbanced.

Note that for a second order plant,the LESO in(6)and(3)is of the third order,wherex3is an estimate off.With a well-tuned observer,the control law is given

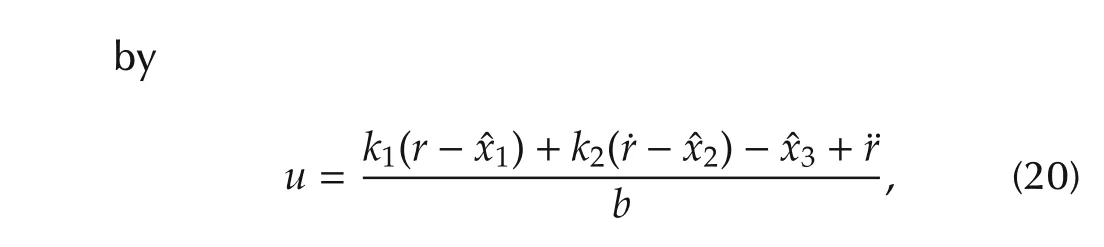
wherek1= ω2c,andk2=2ωc.

The LADRC tracking performance is shown in Fig.5 under three different scenarios:1)fis completely unknown;2)only partial internal dynamics information of the plantis given,i.e.,fpartial=˙y3;3)the internaldynamics of the plantfinis completely known,i.e.,fin=˙y3+yis given.In this simulation,the tuning parameters are ωc=4.5 rad/s and ωo=20 rad/s.Fig.5 shows the tracking errors between the reference and the output for three cases using a step input att=1 s as the excitation and a pulse disturbance with the amplitude of±20,the period of 4 s,the pulse width 5%of the period,and the phase delay of 4 s.From Fig.5,it can be observed that the tracking error of the control loop decreases as more model information is incorporated into the LADRC.

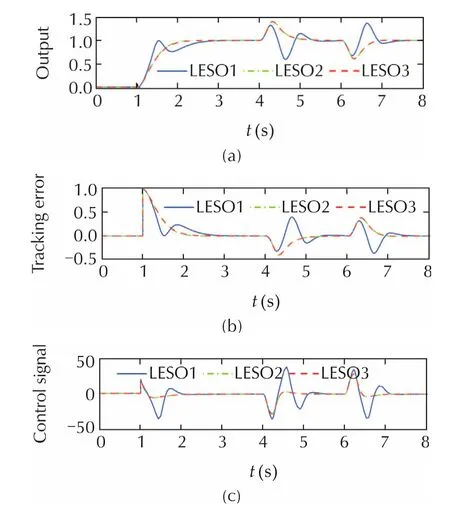
Fig.5 The LADRC performance with different LESOs for the nonlinear system(LESO1:without plant information;LESO2:with partial plant information,i.e.,f partial=˙y3;LESO3:with complete plant information,i.e.,f in=˙y3+y is given).

Note that the system(18)is a nonlinear system.The above simulation demonstrates that ADRC can control the nonlinear system with large uncertainties very well although the ADRC itself is linear.Many other approaches can deal with uncertainties,however,most of them can only handle small uncertainties.ADRC is a very simple and straightforward approach.It is easy to understand by engineers and easy to implement in real applications.From the above simulation,even˙f,i.e.,htends to∞,the ESO gain is still low.Therefore,the ESO is not a high gain observer.

6 Conclusions

In this paper,the time domain formulation and frequency domain understanding of the ADRC are connected.It is shown that the formulation of the ADRC in time domain can be easily understood by engineers with insights in the language of frequency responses,such as the bandwidth and stability margins.From both the frequency responses and the time domain validation,it is clear that the ADRC is unique in its ability of disturbance rejection and in its robustness to large uncertainties in process dynamics.It also shows that the stability characteistics of the ESO and the ADRC can be analyzed directly by solving the differential equations,instead of indirectly by using the standard techniques such as the Lyapunov methods.In doing so,the relationship between the error bounds and the ADRC bandwidth is disclosed.In the ADRC analysis and validation,one can see that the ADRC can handle nonlinear systems with large uncertainties and disturbances without the need of accurate mathematical model of the plant.Partial model information,if given,can and should be incoporated into the ESO for better performance,less noise sensitivity and the reduced bandwidth.

[1] R.Brockett.New issues in the mathematics of control.Mathematics Unlimited–2001 and Beyond.B.Engquist,W.Schimid(eds).Berlin:Springer,2001:189–220.

[2] J.Han.Is it control theory or model theory?Systems Science and Mathematical Sciences,1989,9(4):328–335(in Chinese).

[3] J.Han.A class of extended state observers for uncertain systems.Control and Decision,1995,10(1):85–88(in Chinese).

[4]J.Han.Nonlinear state error feedback control.Control and Decision,1995,10(3):221–225(in Chinese).

[5] J.Han.Auto-disturbance rejection control and its applicationss.Control and Decision,1998,13(1):19–23(in Chinese).

[6]J.Han.Nonlinear design methods for control systems.Proceedings of the 14th IFAC World Congress,Beijing,1999:521–526.

[7]Z.Gao,Y.Huang,J.Han.An alternative paradigm for control system design.Proceedings of the IEEE Conference on Decision and Control,New York:IEEE,2001:4578–4585.

[8] Z.Gao.Active disturbance rejection control:a paradigm shift in feedback control system design.Proceedings of the American Control Conference,New York:IEEE,2006:2399–2405.

[9]Z.Gao.On the centrality of disturbance rejection in automatic control.ISA Transactions,2014,53(4):850–857.

[10]Z.Gao.Active disturbance rejection control:from an enduring idea to an emerging technology.Proceedings of the 10th International Workshop on Robot Motion and Control,Poznan:IEEE,2015:269–282.

[11]J.Han.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900–906.

[12]G.Basile,G.Marro.On the observability of linear,time-invariant systems with unknown inputs.Journal of Optimization Theory and Applications,1969,2(6):410–415.

[13]C.Johnson.Accommodation of external disturbances in linear regulator and servomechanism problems.IEEE Transactions on Automatic Control,1971,16(6):635–644.

[14]G.Hostetter,J.Meditch.On the generalization of observers to systems with unmeasurable,unknown inputs.Automatica,1973,9(6):721–724.

[15]C.Johnson.Theory of disturbance-accommodating controllers.Control and Dynamic Systems,1976,12:387–489.

[16]V.Gourishangkar,P.Kudva,K.Ramar.Reduced-order observers for multivariable systems with inaccessible disturbance inputs.International Journal of Control,1977,25(2):311–319.

[17]P.C.Muller.Indirect measurements of nonlinear effects by state observers.Nonlinear Dynamics in Engineering Systems,Berlin:Springer,1990:205–215.

[18]J.Profeta,W.Vogt,M.Mickle.Disturbance estimation and compensation in linear systems.IEEE Transaction on Aerospace and Electronic Systems,1990,26(2):225–231.

[19]J.Chen,R.J.Patton,H.Zhang.Design of unknown input observers and robust fault detection filters.International Journal of Control,1995,63(1):85–105.

[20]T.Umeno,Y.Hori.Robust speed control of DC servo motors using modern two degrees-of-freedom controller design.IEEE Transactions on Industrial Electronics,1991,38(5):363–368.

[21]Y.Hori,K.Shimura,M.Tomizuka.Position/force control of multiaxis manipulator based on the TDOF robust servo controller for each joint.Proceedings of the American Control Conference ACC/WM9,New York:IEEE,1992:753–757.

[22]H.Lee,M.Tomizuka.Robust motion controller design for highaccuracy positioning systems.IEEE Transactions on Industrial Electronics,1996,43(1):48–55.

[23]T.Mita,M.Hirata,K.Murata,et al.H∞control versus disturbance-observer-based control.IEEETransactionson Industrial Electronics,1998,45(3):488–495.

[24]R.Bickel,M.Tomizuka.Passivity-based versus disturbance observer based robot control:equivalence and stability.ASME Journal of Dynamics Systems,Measurement,and Control,1999,121(1):41–47.

[25]E.Schrijver,J.van Dijk.Disturbance observers for rigid mechanical systems:equivalence,stability,and design.ASME Journal of Dynamics Systems,Measurement,and Control,2002,124(4):539–548.

[26]Y.Choi,K.Yang,W.K.Chung,et al.On the robustness and performance of disturbance observers for second-order systems.IEEE Transactions on Automatic Control,2003,48(2):315–320.

[27]K.Yang,Y.Choi,W.Chung.On the tracking performance improvement of optical disk drive servo systems using errorbased disturbance observer.IEEE Transactions on Industrial Electronics,2005,52(1):270–279.

[28]S.Kwon,W.K.Chung.Robust performance of the multiloop perturbation compensator.IEEE/ASME Transaction on Mechatronics,2002,7(2):190–200.

[29]S.Kwon,W.K.Chung.A discrete-time design and analysis of perturbation observer for motion control applications.IEEE Transactions on Control Systems Technology,2003,11(3):399–407.

[30]S.Kwon,W.K.Chung.Combined synthesis of state estimator and perturbation observer.ASME Journal of Dynamic Systems,Measurement,and Control,2003,125(1):19–26.

[31]S.Kwon.Robust Kalman filtering with perturbation estimation process.Proceedings of the American Control Conference,New York:IEEE,2006:997–1002.

[32]A.Radke,Z.Gao.A survey of state and disturbance observers for practitioners.Proceedings of the American Control Conference,New York:IEEE,2006:5183–5188.

[33]W.Chen,J.Yang,L.Guo,et al.Disturbance observer-based control and related methods:an overview.IEEE Transactions on Industrial Electronics,2016,63(2):1083–1095.

[34]Q.Zheng,L.Gao,Z.Gao.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics.Proceedingsofthe46thIEEEConference on Decision and Control,New Orleans:IEEE,2007:3501–3506.

[35]Z.Zhao,B.Guo.On convergence of nonlinear active disturbance rejection control for SISO nonlinear systems.Journalof Dynamical and Control Systems,2016,22(2):385–412.

[36]Y.Huang,W.Xue.Active disturbance rejection control:methodology and theoretical analysis.ISA Transactions,2014,53(4):963–976.

[37]B.Guo,H.Zhou.The active disturbance rejection control to stabilization for multi-dimensional wave equation with boundary control matched disturbance.IEEE Transactions on Automatic Control,2015,60(1):143–157.

[38]B.Guo,F.Jin.The active disturbance rejection and sliding mode control approach to the stabilization of the Euler-Bernoulli beam equation with boundary input disturbance.Automatica,2013,49(9):2911–2918.

[39]B.Guo,Z.Zhao.On convergence of the nonlinear active disturbance rejection control for MIMO systems.SIAM Journal on Control and Optimization,2013,51(2):1727–1757.

[40]B.Guo,Z.Zhao.On the convergence of extended state observer fornonlinearsystems with uncertainty.Systems&ControlLetters,2011,60(6):420–430.

[41]Z.Gao.Scaling and parameterization based controller tuning.ProceedingsoftheAmericanControlConference,New York:IEEE,2003:4989–4996.

[42]G.Tian,Z Gao.Frequency response analysis ofactive disturbance rejection based control system.IEEE Multi-conference on Systems and Control,New York:IEEE,2007:1167–1172.

[43]J.Csank,Z Gao.Uncertainty reduction through active disturbance rejection.Proceedings of the American Control Conference,New York:IEEE,2008:3689–3694.

[44]J.Tatsumi,Z Gao.On the enhanced ADRC design with a low observer bandwidth.Proceedings of the Chinese Control Conference,New York:IEEE,2013:297–302.

[45]W.Xue,Y.Huang.Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems.ISA Transactions,2015,58:133–154.

[46]Q.Zheng,L.Dong,D.H.Lee,et al.Active disturbance rejection control and implementation for MEMS gyroscopes.IEEE Transactions on Control Systems Technology,2009,17(6):1432–1438.

[47]Q.Zheng,Z.Chen,Z Gao.A practical dynamic decoupling controlapproach.ControlEngineeringPractice,2009,17(9):1016–1025.

[48]Q.Zheng,Z.Gao.An energy saving,factory-validated disturbance decoupling control design for extrusion processes.Proceedings of the 10th World Congress on Intelligent Control and Automatio,Beijing:IEEE,2012:2891–2896.

[49]Q.Zheng.On Active Disturbance Rejection Control:Stability Analysis and Applications in Disturbance Decoupling Control.Ph.D.thesis.Cleveland:Cleveland State University,2009.

[50]Q.Zheng,L.Gao,Z.Gao.On validation of extended state observer through analysis and experimentation.ASME Journalof Dynamic Systems,Measurement,and Control,2012,134(2):DOI 10.1115/1.4005364.