Extended state observer for uncertain lower triangular nonlinear systems subject to stochastic disturbance

Zehao WU,Baozhu GUO

Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

The extended state observer(ESO)is the most important component of active disturbance rejection control(ADRC),an emerging control technology proposed by Han in his pioneer work[1].ADRC is now acknowledged to be an effective control strategy in dealing with systematically so called “total disturbance”which can include the coupling between unknown system dynamics,external disturbance,and the superadded unknown part of control input,in a large scale.The most remarkable feature of ADRC lies in its estimation/cancellation nature,where the total disturbance is considered as an extended state and is estimated,in real time,through ESO.The total disturbance is finally cancelled(compensated)in the feedback loop by its estimation.This estimation/cancellation nature of ADRC makes it capable of eliminating the uncertainty before it causes negative effect to control plant and the control energy can therefore be saved significantly in engineering applications.The idea of ADRC has been attracting more attention by the industry practitioners as presented in an up-to-date survey paper[2].The numerous concrete applications in different fields include flexible joint manipulator control[3],control of a model-scale helicopter[4],omnidirectional mobile robot control[5],vibrational control in MEMS gyroscopes[6],or control system in superconducting RF cavities[7],as reviewed,among many others,in[8].On the other hand,some progresses have also been made in theoretical foundations,see[9–16],name just a few.

The first ESO is designed in[17]as follows:

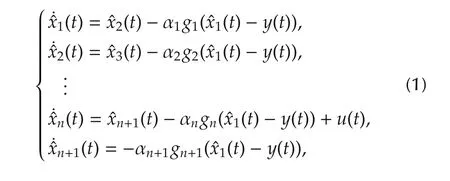
for the followingn-dimensional single input and single output(SISO)nonlinear system

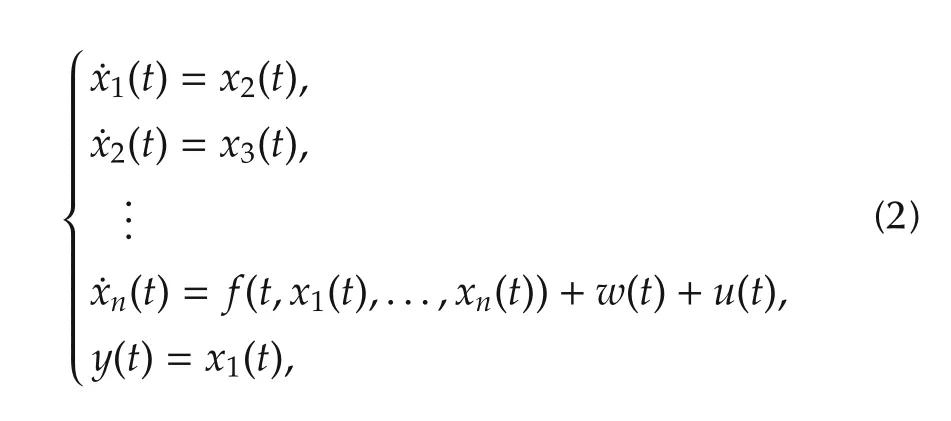
wheref:[0,∞)×Rn→ R is possibly an unknown function,w(t)the external disturbance,y(t)the measured output,andu(t)is the control input.

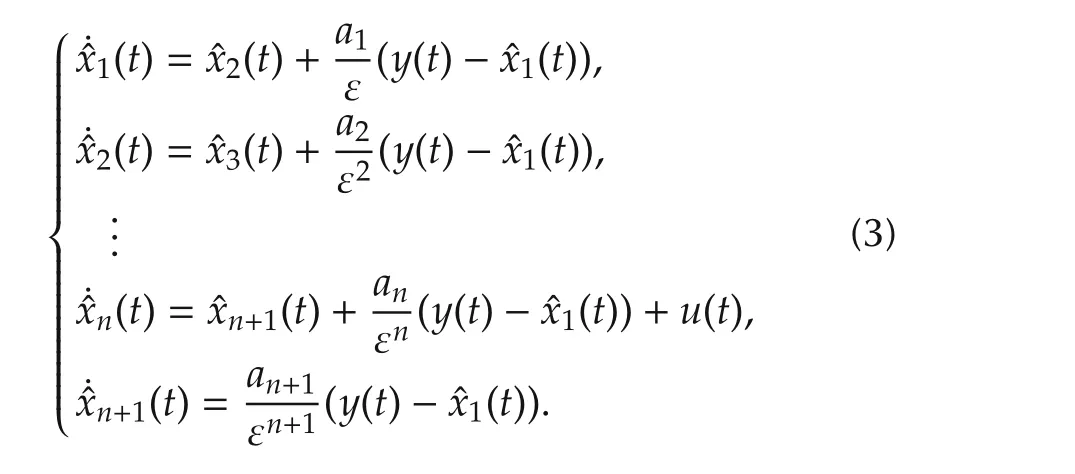
The ESO(3)(with linear gain functions)is thus said to be linear ESO(LESO).The convergence of LESO(3)for SISO systems is presented in[19,20].

As a special case of ESO(1)and a nonlinear generalization of LESO(3),a nonlinear ESO(NLESO in short)of the following:

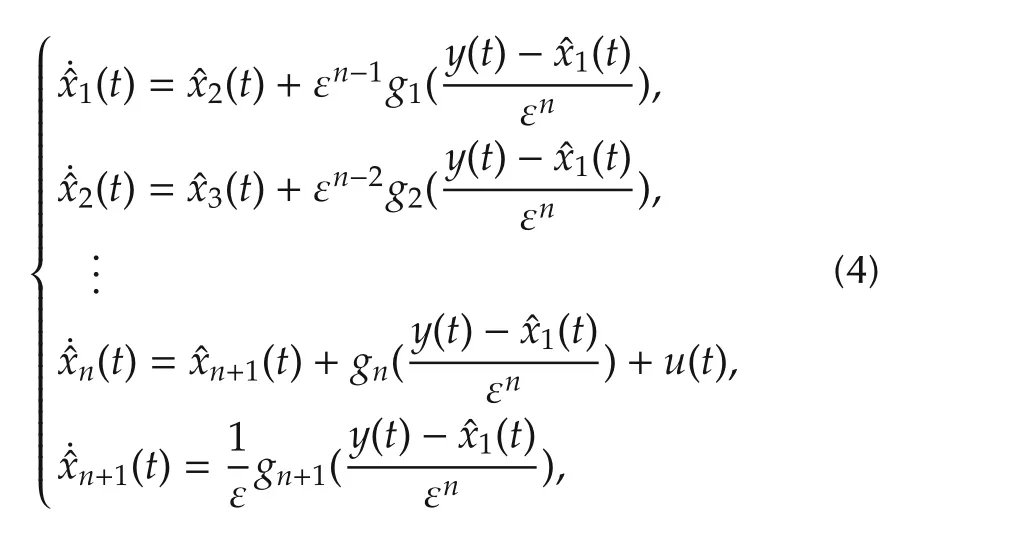
is proposed in[9],where convergence of NLESO(4)for SISO systems is concluded.Shortly afterwards,a series of convergence results on NLESO for more general deterministic systems are developed,see,for instance,[10–13].

Although great progress has been achieved,most of the literatures including the aforementioned ones,however,are focused mainly on deterministic systems,and little attention is paid to stochastic counterparts.This motivates us,in this paper,to consider ESO for a class of uncertain stochastic nonlinear systems where the external stochastic disturbance satisfying an Ito-type stochastic differential equation.A typical example of such kind of exogenous disturbance is the “colored noise”whose fundamental noise sources through various feedback mechanisms may be regarded as white so that it can be produced by passing the white noise through a filter,described by an Ito-type stochastic differential equation,see,for instance,[21,22].Actually,“colored noise”exists in many practical systems such as physical model systems[23,24]and chemical model systems[25].The paper[16]focuses on the filtering problem of general discrete nonlinear uncertain systems with nonlinear un-known dynamics,stochastic process and measurement noises,where the extended state filter(ESF)is constructed to estimate timely the uncertainties of the system.In this paper,however,the bounded continuous time noise,considered as part of the stochastic total disturbance,is estimated by ESO.Precisely,the system that we consider is an uncertain lower triangular nonlinear system with external stochastic disturbance as

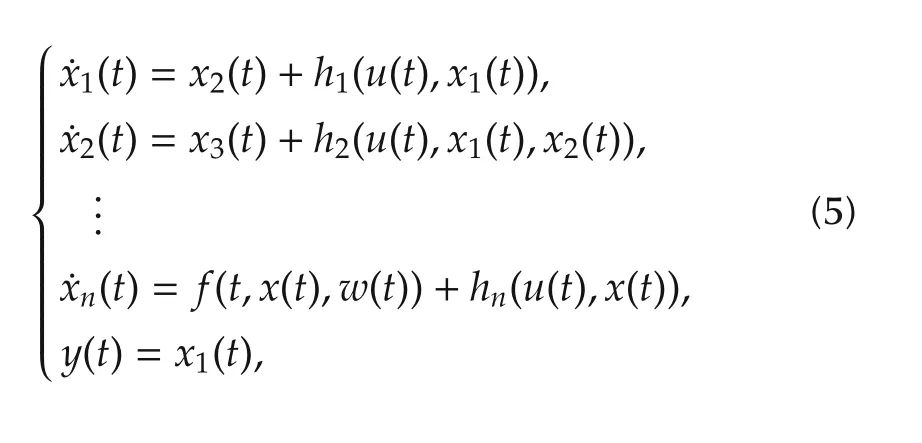
wherex(t)=(x1(t),...,xn(t))T∈Rn,u(t)∈Rm,andy(t)=x1(t)∈R are the state,control(input),and output(measurement)of system,respectively;The functionshi:Rm+i→R(i=1,2,...,n)are known,whereasf:[0,∞)×Rn+1→ R is possible unknown measurable;Thew(t)∈R is used to describe the external stochastic disturbance which is assumed to satisfy the following uncertain stochastic differential equation:

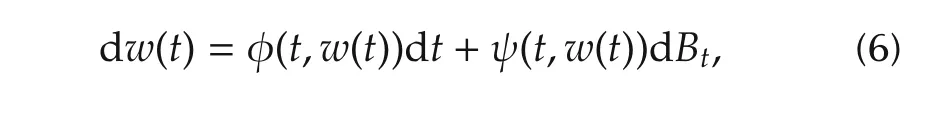
wherew(0)=w0and{Bt}t?0is an one-dimensional standard Brownian motion defined on a complete probability space(Ω,F,{Ft}t?0,P)with Ω being a sample space,F a σ-field,{Ft}t?0a filtration,andPthe probability measure;The functions φ :[0,∞)× R → R,ψ:[0,∞)×R→ R are unknown measurable functions.

We proceed as follows.In the next section,Section 2,we design a NLESO to estimate both state and stochastic total disturbance.The mean-square convergence is proved.As a direct consequence,we conclude convergence for LESO.In Section 3,a special kind of ESO is applied to system(5)where the stochastic total disturbance includes external stochastic disturbance only.The corresponding convergence is developed.In Section 4,some numerical experiments are carried out to illustrate effectiveness of the proposed approach.

2 Convergence of extended state observer

Motivated from deterministic case[13],we introduce a NLESOproposed in[13]with constanthigh gain tuning parameter for system(5)as follows:

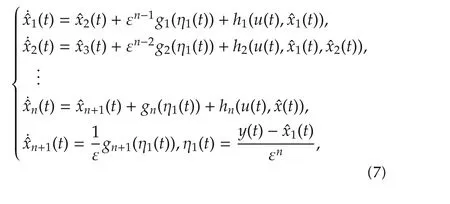
wheregi∈C(R;R)(i=1,2,...,n+1)are designed functions to be specified later,ε＞ 0 is the tuning parameter,andxn+1(t)is used to estimate the stochastic total disturbancexn+1(t)?f(t,x(t),w(t)).Here and throughout the paper,we always drop ε for the solution to(7)by abuse of notation without confusion.

To obtain convergence of NLESO(7)for system(5),we need some assumptions.

Assumption 1 is a prior assumption about the functionshi(·),f(·),φ(·),and ψ(·).

Assumption 1f(·)is twice continuously differentiable with respect to its arguments,and there exist(known)constantsCi＞0(i=1,2)and non-negative functionsζ1∈C(Rm;R),ζ2∈C(Rn;R),ζ3,ζ4∈C(R;R)such that for allt?0,x∈Rn,w∈R,

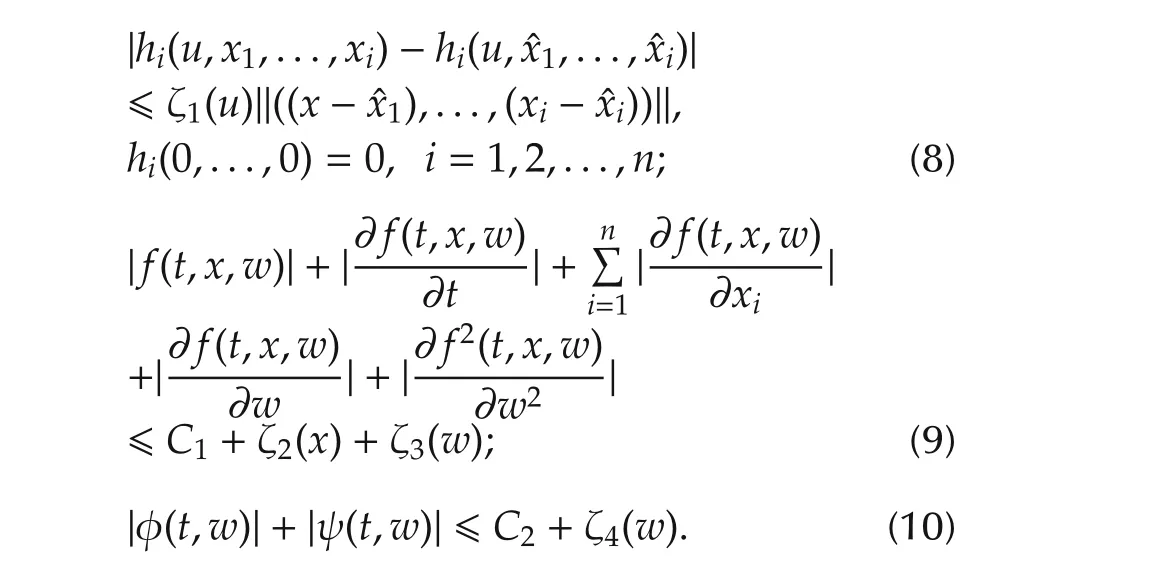
Assumption 2 is a prior assumption about the control inputu(t)and the external stochastic disturbancew(t).

Assumption 2There exists a(known)constantM?0 such that|u(t)|+|w(t)|?Malmost surely for allt?0.

Remark 1Since the stochastic disturbancew(t)is regarded as part of an extended state variable of system(5)to be estimated by ESO,it is reasonable to assume that thew(t)itself and its“variation”(or differential)are bounded.It is also easy to verify that many practical deterministic disturbances such as “cos(a+bt)”,“sin(a+bt)”and stochastic disturbances such as “cos(at+bBt)”,“sin(at+bBt)”satisfy the assumption,wherea,bare con-stants and the deterministic disturbances are covered by letting ψ(·)≡ 0 and φ(·)be independent ofwin(6).

Assumption 3 is on the designed functionsgi(·)’s in ESO(7).

Assumption 3There exist constants λi(i=1,...,4)and twice continuously differentiable functionV:Rn+1→R which is positive definite and radially unbounded such that

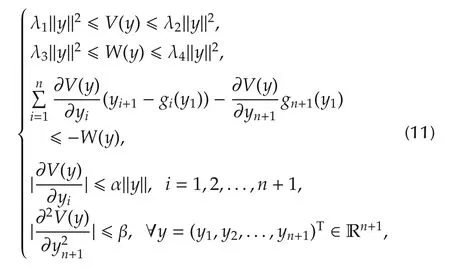
for some nonnegative continuous functionW:Rn+1→R and constants α,β ＞ 0.

Assumption 3 guarantees that the zero equilibrium of the following system:

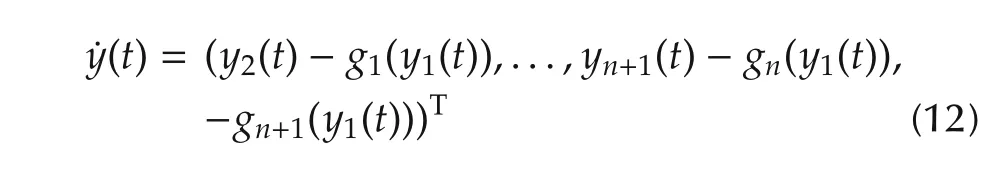
is asymptotically stable.

where Γ ＞ 0 is an ε-independent constant.

ProofSet

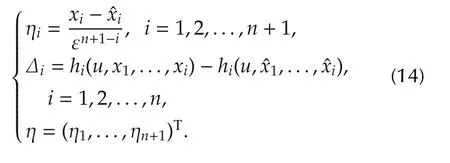
By Assumptions 1 and 2,we suppose without loss of

By Assumptions 1 and 2,there exists a constantC4＞0 such that

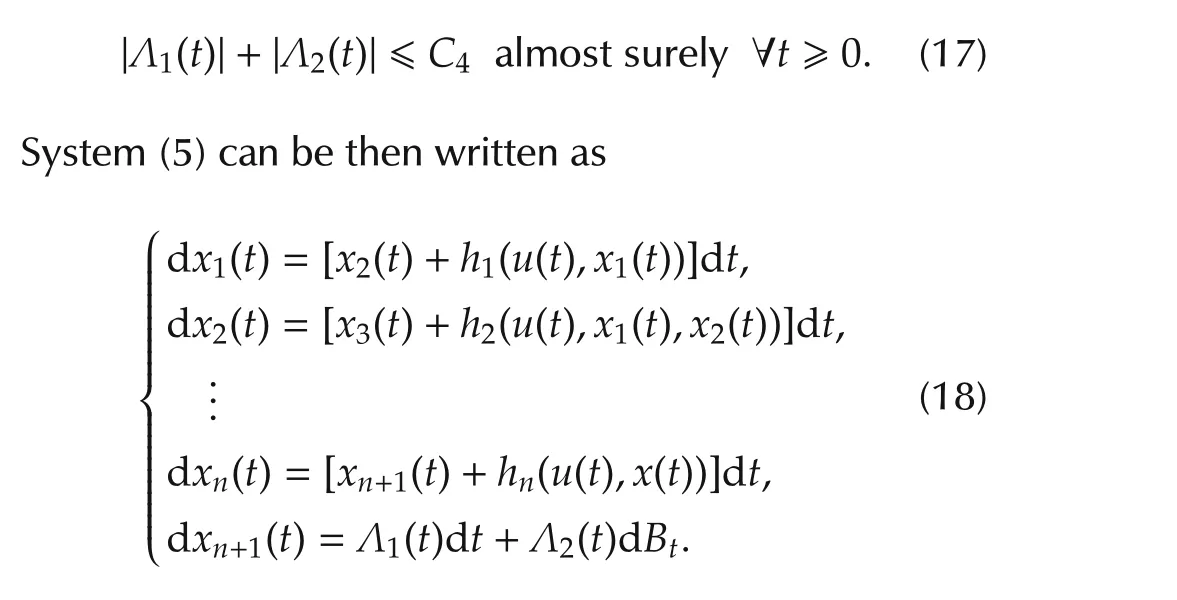
A straightforward computation shows that η(t)satisfies

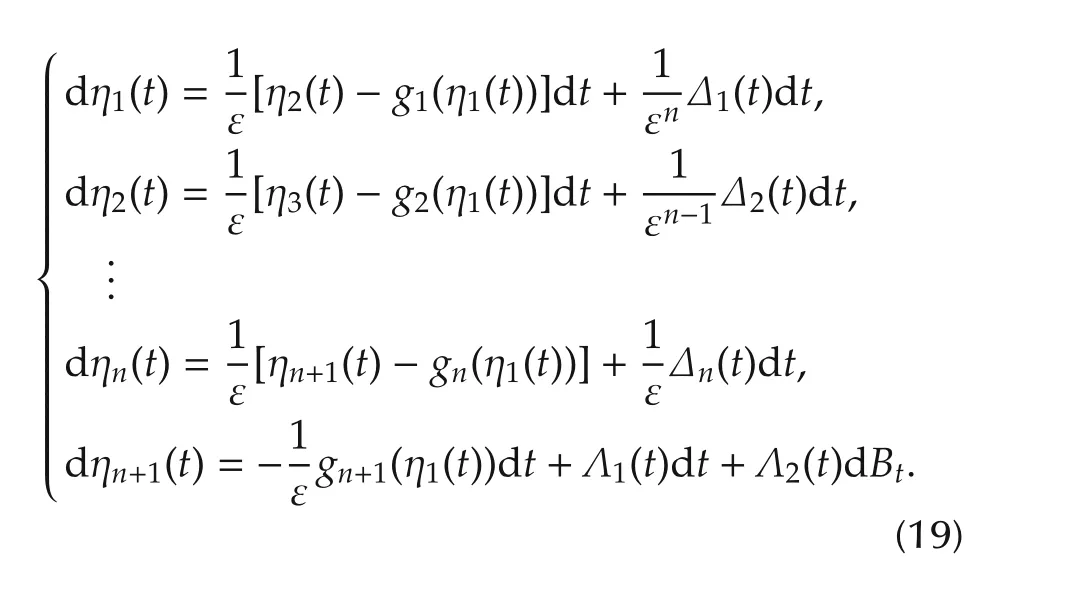
We apply Ito’s formula toV(η(t))with respect totalong the solution η(t)of system(19)to obtain

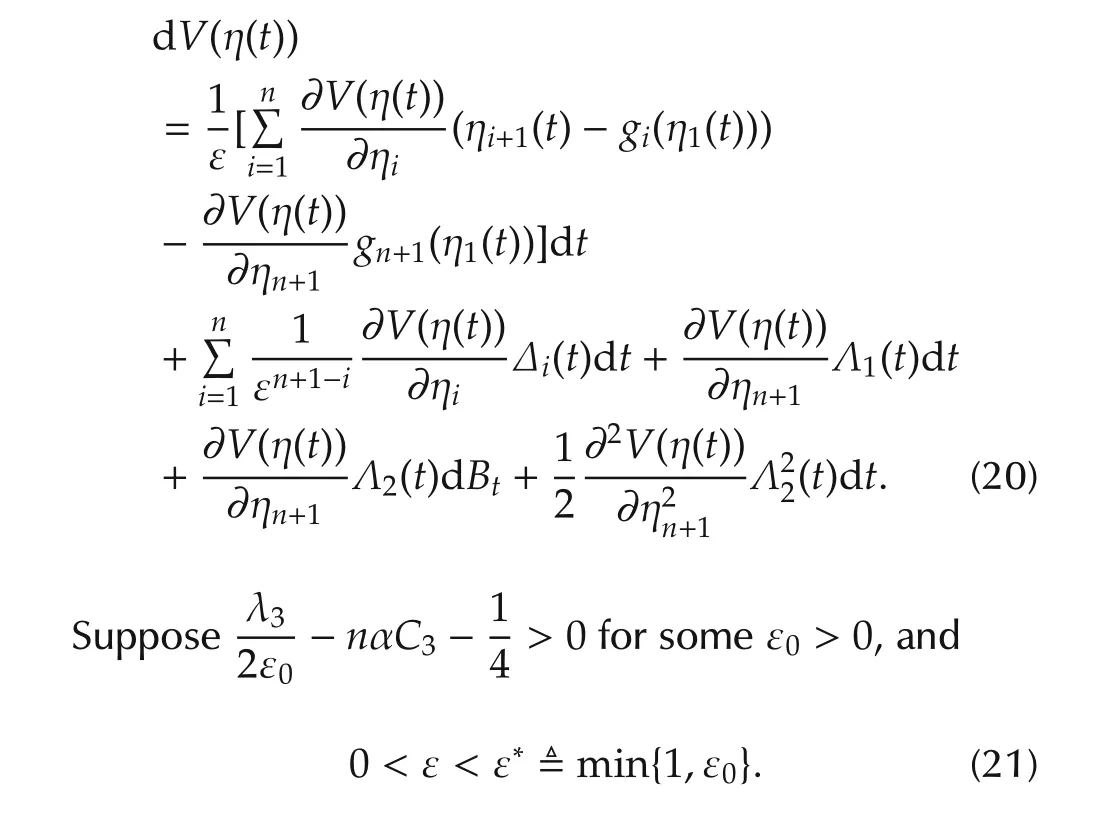
By(15),(17),(20),and Assumption 3,it follows that dEV(η(t))

Since both the first term and the second one of the righthand side of(23)are bounded by ε multiplied by an ε-independent constant,there exists an ε-independent constant γ ＞ 0 such that for allt∈ [a,∞),

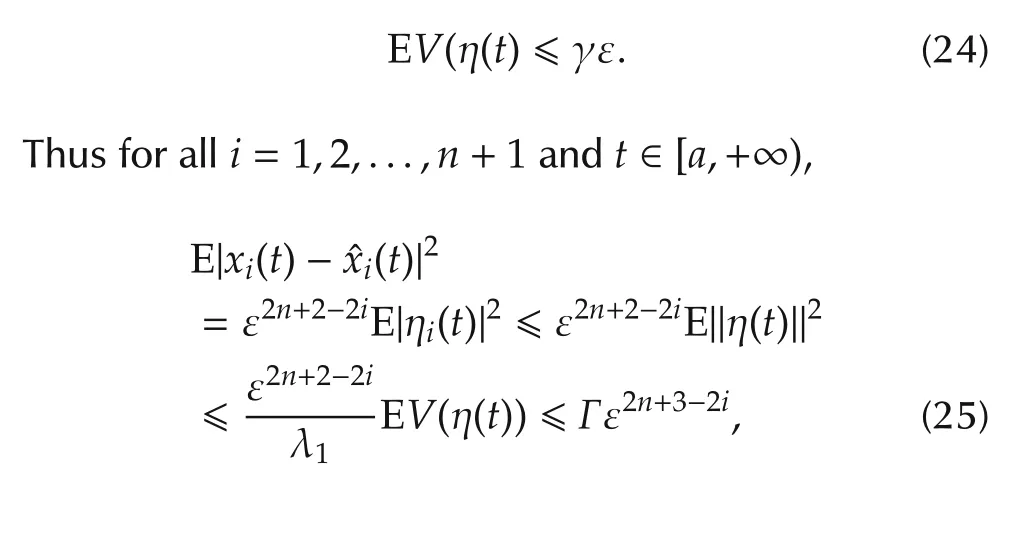
The simplest ESO is certainly the LESO which is a special case of(7):

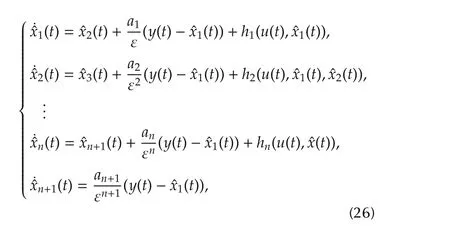
wheregi(·)?s(i=1,...,n+1)in ESO(7)are linear functions:gi(r)=air,r∈R.Define the matrix as follows:

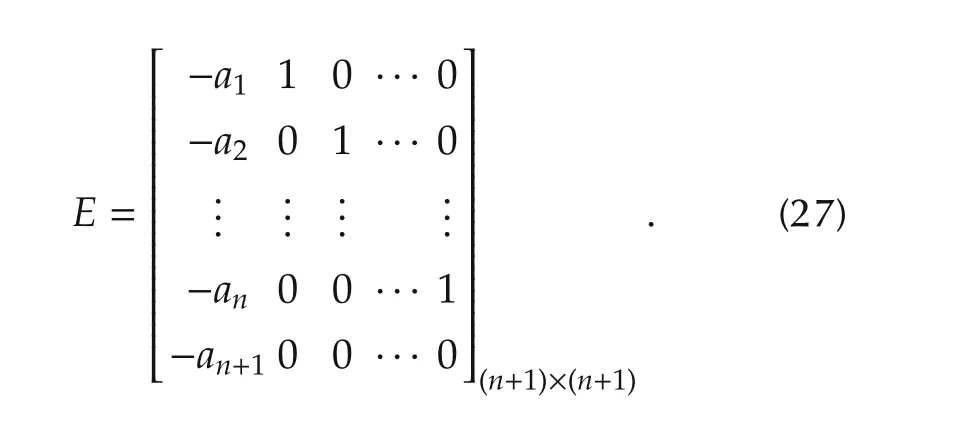
where Γ ＞ 0 is an ε-independent constant.

ProofLetQbe the unique positive definite matrix solution to the Lyapunov equationQE+ETQ=-I(n+1)×(n+1)for(n+1)-dimensional identity matrixI(n+1)×(n+1).Define the Lyapunov functionsV,W:Rn+1→R byV(y)=yTQy,W(y)=yTyfory∈Rn+1.It is easy to verify that all conditions of Assumption 3 are satisfied.The result then follows directly from Theorem 1. ?

Remark 2Whenhi(·)≡ 0(i=1,2,...,n),system(5)is of the form:

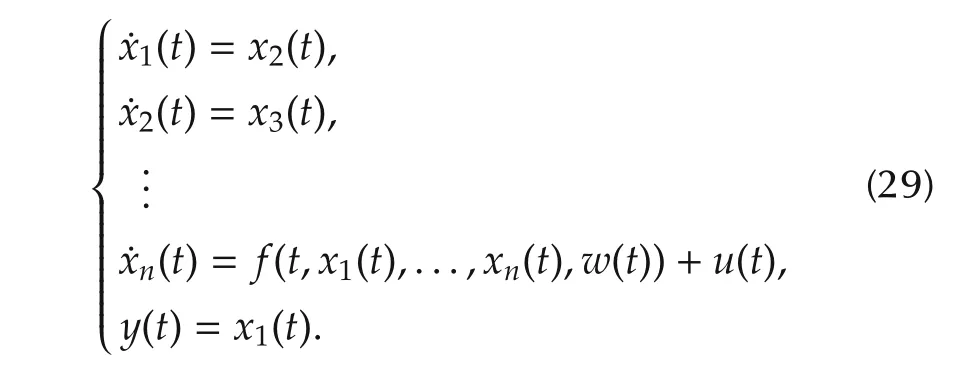
We thus conclude the results of[26]by Theorem1 and Corollary 1.

3 Extended state observer utilizing known part

Although theoretically,ESO spans the concept of disturbance which can include even the parts which are hardly to be treated by practitioner,ESO should utilizes the known information of the plant as much as possible to improves its performance.In this section,a special ESO is considered,where the system functionf(t,x,w)=f1(t,x)+f2(w),withf1(·)being known.In other words,the total disturbance comes from external stochastic disturbance only.In this case,the NLESO in this case can be modified as

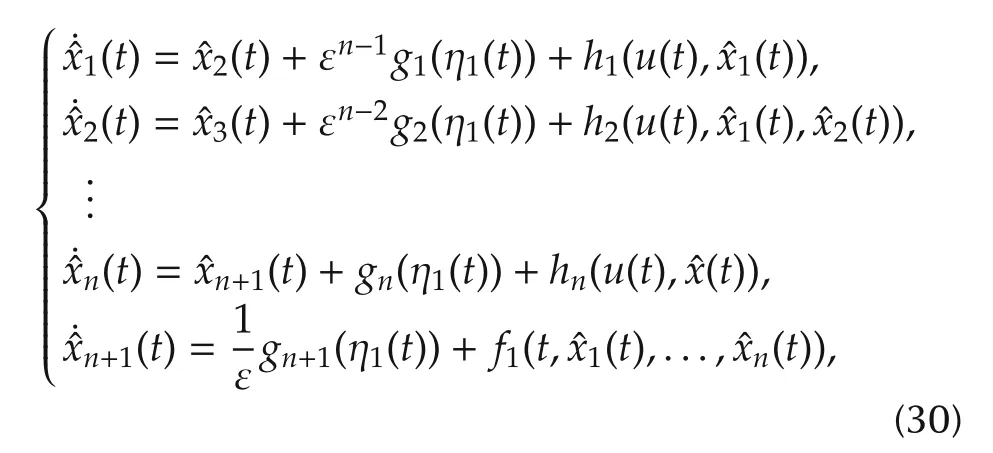
wherexn+1(t)is again used to estimate the stochastic total disturbancexn+1(t)?f2(w(t)).

To have convergence of NLESO(30),we replace Assumption 1 by Assumption 1＊.

Assumption 1＊f2(·)is twice continuously differentiable with respect to its argument and there exist(known)constantsDi＞0(i=1,...,5)and nonnegative functions ζ5,ζ6∈C(R;R)such that for allt?0,x∈Rn,w∈R,

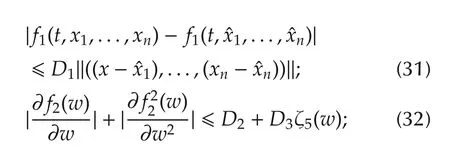
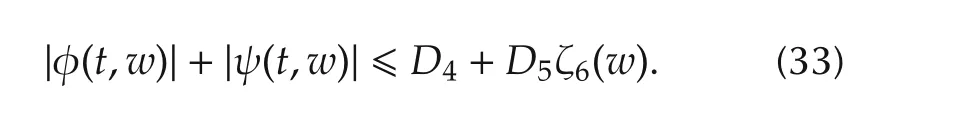
By Assumptions 1＊and 2,there exists a constantD6＞ 0 such that

A straightforward computation shows that η(t)satisfies

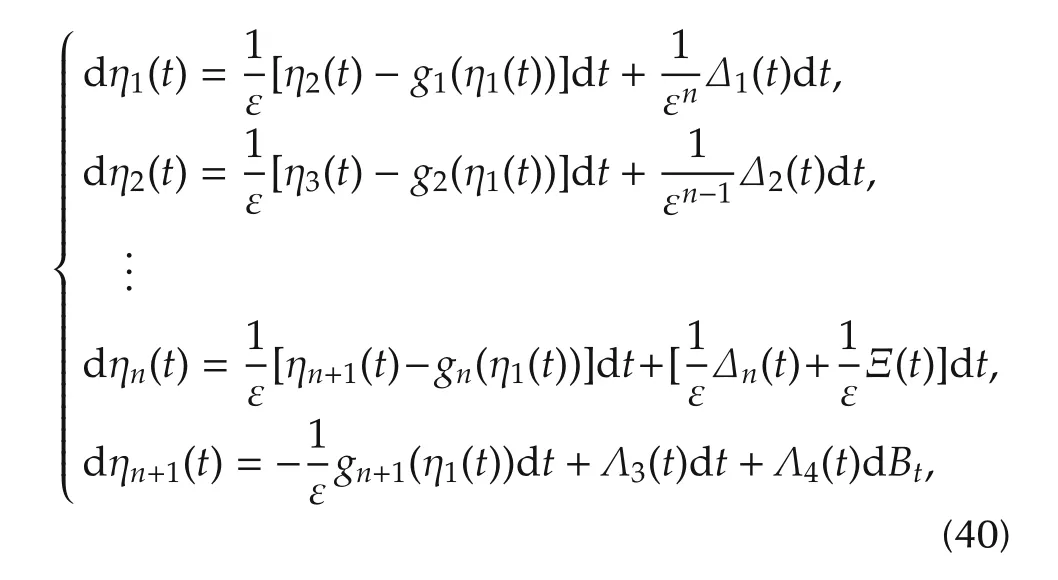
where ηi(t)(i=1,2,...,n+1)and Δi(t)(i=1,2,...,n)are defined as that in(14).By Assumption 3,we apply Ito’s formula toV(η(t))with respect totalong the solution η(t)of system(40)to obtain

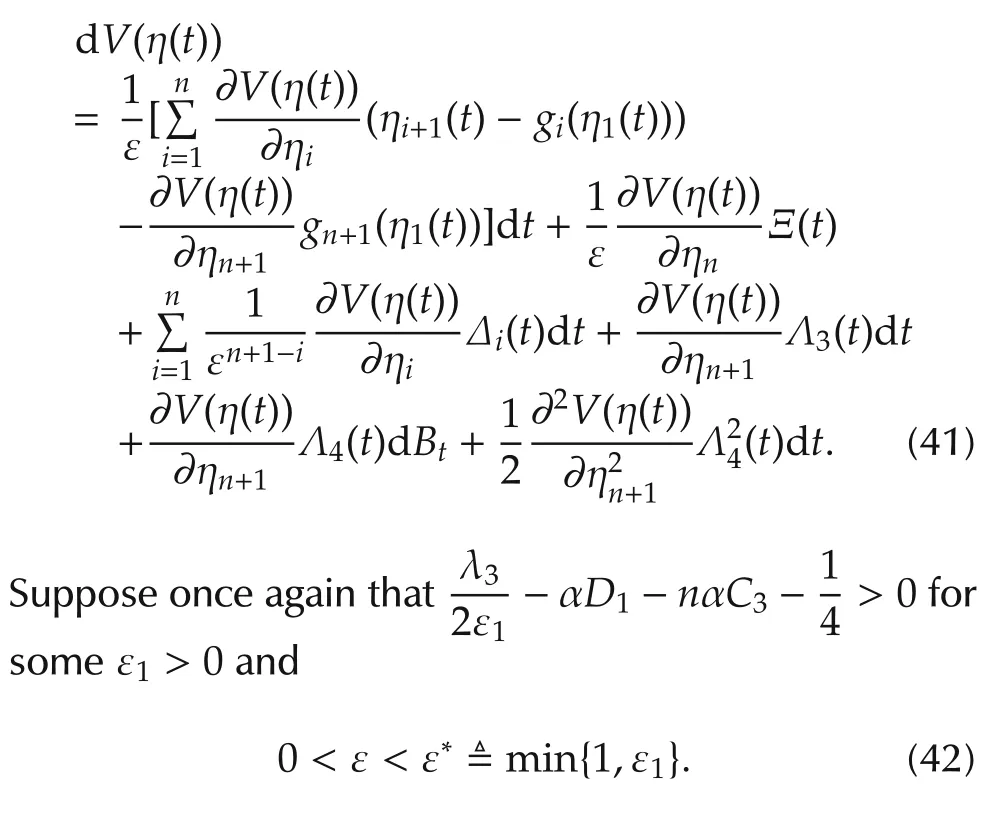
Then it follows from(15),(36),(39),and Assumption 3 that

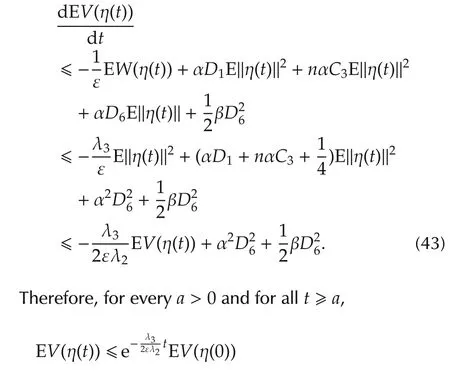
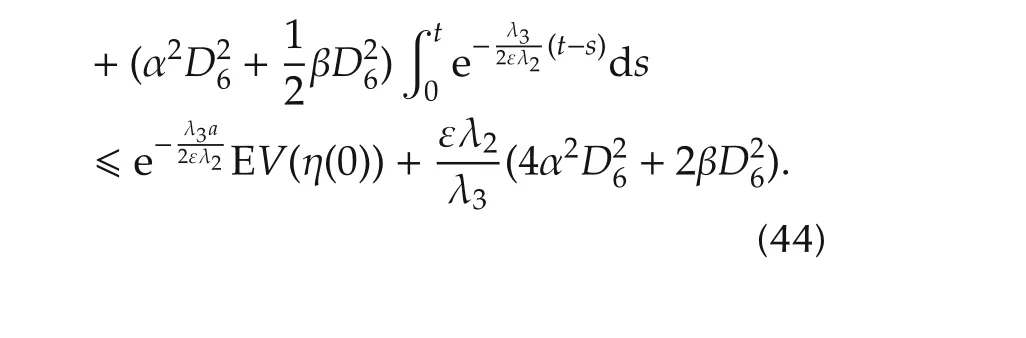
Since both the first term and the second one of the righthand side of(44)are bounded by ε multiplied by an ε-independent constant,there exists an ε-independent constant ξ ＞ 0 such that for allt∈ [a,∞),

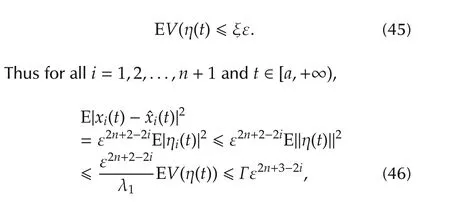
Similarly,the corresponding LESO of(30)is as follows:

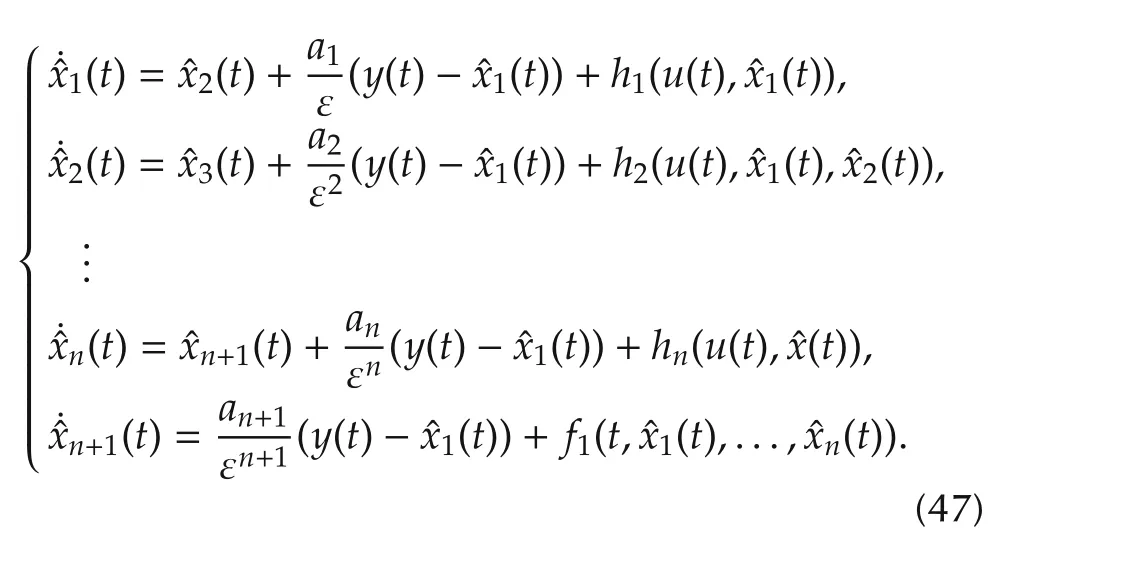
Similarly to the proof of Corollary 1,we have immediately Corollary 2.

where Γ ＞ 0 is an ε-independent constant.

4 Numerical simulation

In this section,we present an example to illustrate the effectiveness ofthe proposed ESOto estimate both state and stochastic total disturbance.Consider the following second order uncertain lower triangular nonlinear system with exogenous stochastic disturbance:

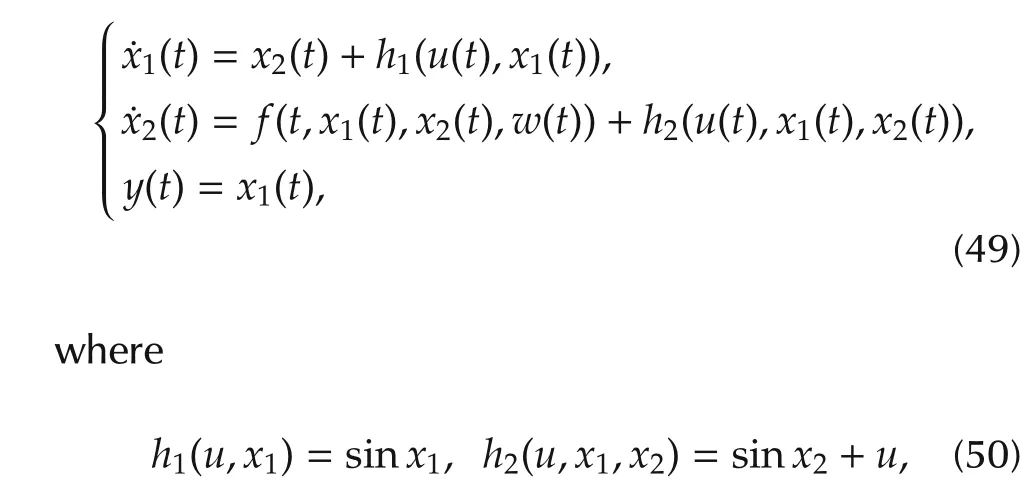
are known functions,whereas the stochastic total disturbancex3?f(t,x1,x2,w)is completely unknown.We suppose without loss of generality that the bounded inputu(t)is also disturbed by stochastic noise:

First,we notice that the corresponding matrix in(27)for the linear part of(52)

is Hurwitz with all eigenvalues being identical to-1.In this case,gi(·)in(7)can be specified as

is the positive definite solution to the Lyapunov equationPE+ETP=-IforEgiven by(54).Similar to[9],Assumption 3 in(11)is satisfied for this example.Hence(52)serves as a well-defined NLESO for(49)from Theorem 1.The Milstein approximation method[27]is used to discretize systems(49)and(52).Figs.1–3 display the numerical results for(49)and(52)where we take

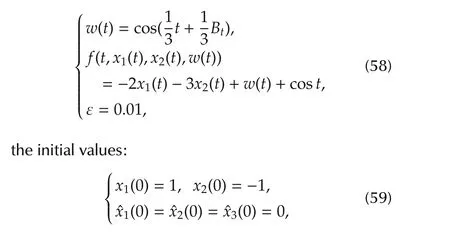
and the time discrete step as

is also Hurwitz.In addition,since the control input and external stochastic disturbance are uniformly bounded almost surely,the solution to system(49)is also uniformly bounded almost surely.Therefore,all the Assumptions in Theorem 1 are satisfied.It is seen from Figs.1–3 that the NLESO(52)is very effective in tracking system(49)not only for the state(x1(t),x2(t))but also for the extended state(total disturbance)x3(t)defined by

It is observed from Fig.1 that the tracking effect forx1(t)is the best,andx2(t)the second from Fig.2,andx3(t)the third from Fig.3.These are coincident with theoretical estimation(13)that the estimation errors forx1(t),x2(t),andx3(t)are bounded by O(ε5),O(ε3),and O(ε)in practical mean square sense,respectively.In addition,the peaking values near the initial stages are observed in both Figs.2 and 3,which can be reduced by time-varying gain approach presented in the recent paper[28].

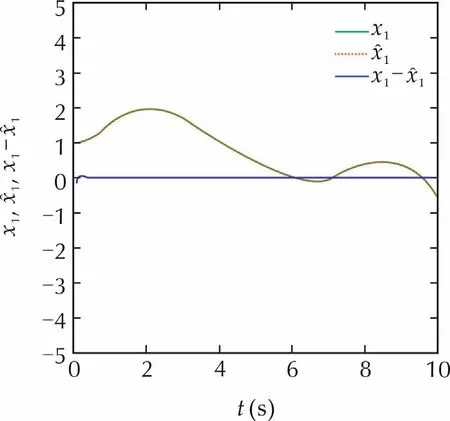
Fig.1 The tracking effect for state x1.

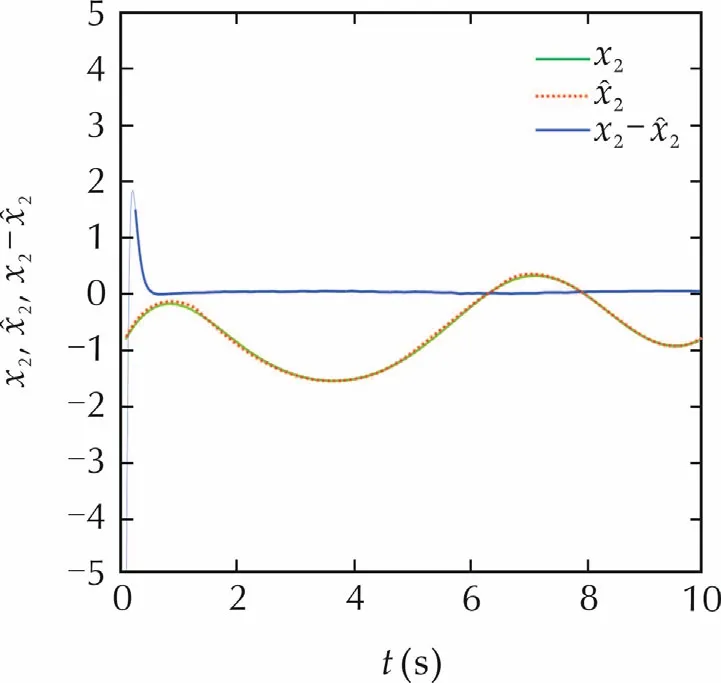
Fig.2 The tracking effect for state x2.

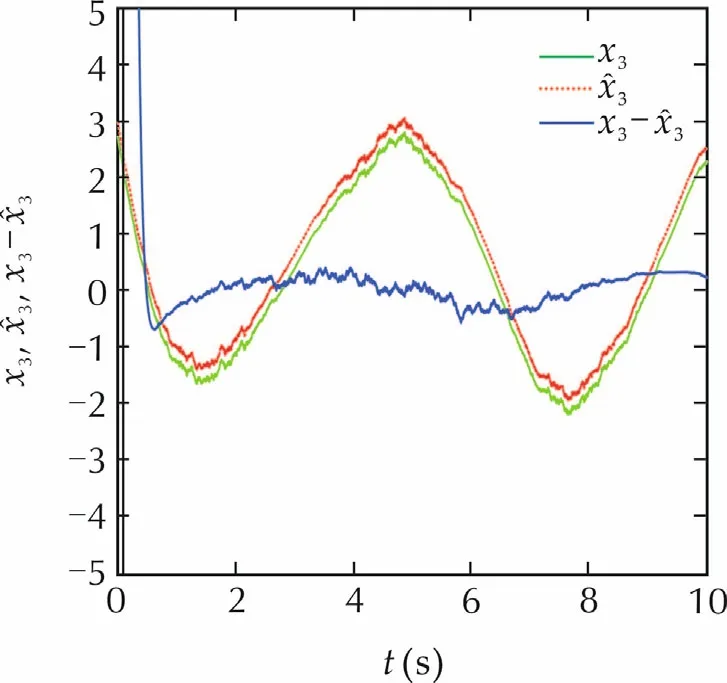
Fig.3 The tracking effect for stochastic total disturbance x3.

5 Conclusions

In this paper,an extended state observer(ESO)is designed for a class of lower triangular nonlinear systems with large stochastic total disturbance which comes from both internal unknown dynamics and external stochastic disturbance.The ESO is used to estimate,in real time,not only the state but also the stochastic total disturbance by the measured output.The meansquare convergence of both nonlinear ESO and linear ESO are presented.In addition,a special kind of ESO is constructed for a class of lower triangular nonlinear systems where the stochastic total disturbance includes external stochastic disturbance only.The corresponding mean-square convergence is also concluded.The numerical simulations validate the theoretical results.

[1]J.Han.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900–906.

[2] Z.Gao.On the centrality of disturbance rejection in automatic control.ISA Transactions,2014,53(4):850–857.

[3]R.Madonski,M.Kordasz,P.Sauer.Application of a disturbance rejection controller for robotic-enhanced limbre habilitation trainings.ISA Transactions,2014,53(4):899–908.

[4]F.Leonard,A.Martini,G.Abba.Robust nonlinear controls of model-scale helicopters under lateral and vertical wind gusts.IEEE Transactions on Control Systems Technology,2012,20(1):154–163.

[5]H.Sira-Ram´ırez,C.L´opez-Uribe,M.Velasco-Villa.Linear observer-based active disturbance rejection control of the omnidirectional mobile robot.Asian Journal of Control,2012,15(1):51–63.

[6]L.Dong,D.Avanesian.Drive-mode control for vibrational MEMS gyroscopes.IEEE Transactions on Industrial Electronics,2009,56(4):956–963.

[7]J.Vincent,D.Morris,N.Usher,et al.On active disturbance rejection based control design for superconducting RF cavities.Nuclear Instruments and Methods in Physics Research–Section A,2011,643(1):11–16.

[8]R.Madonski,P.Herman.Survey on methods of increasing the efficiency of extended state disturbance observers.ISA Transactions,2015,56:18–27.

[9]B.Guo,Z.Zhao.On the convergence of extended state observer fornonlinearsystems with uncertainty.Systems&ControlLetters,2011,60(6):420–430.

[10]B.Guo,Z.Zhao.On convergence of the nonlinear active disturbance rejection control for MIMO systems.SIAM Journal on Control and Optimization,2013,51(2):1727–1757.

[11]B.Guo,Z.Zhao.On convergence of non-linear extended state observer for multi-input multi-output systems with uncertainty.IET Control Theory&Applications,2012,6(15):2375–2386.

[12]Z.Zhao,B.Guo.Active disturbance rejection control approach to stabilization of lower triangular systems with uncertainty.International Journal of Robust and Nonlinear Control,2016,26(11):2314–2337.

[13]Z.Zhao,B.Guo.Extended state observer for uncertain lower triangular nonlinear systems.Systems&Control Letters,2015,85:100–108.

[14]Y.Huang,W.Xue.Active disturbance rejection control:methodology and theoretical analysis.ISA Transactions,2014,53(4):963–976.

[15]W.Xue,Y.Huang.On performance analysis of ADRC for a class of MIMO lower-triangular nonlinear uncertain systems.ISA Transactions,2014,53(4):955–962.

[16]W.Bai,W.Xue,Y.Huang,et al.Extended state filter design for general nonlinear uncertain systems.Proceedings of the 54th Annual Conference of the Society of Instrument and Control Engineers of Japan(SICE),Hangzhou:IEEE,2015:712–717.

[17]J.Han.A class of extended state observers for uncertain systems.Control and Decision,1995,10(1):85–88(in Chinese).

[18]Z.Gao.Scaling and bandwith-parameterization based controller tuning.Proceedings of the American Control Conference,New York:IEEE,2006:4989–4996.

[19]X.Yang,Y.Huang.Capability of extended state observer for estimating uncertainties.Proceedings of the American Control Conference,New York:IEEE,2009:3700–3705.

[20]Q.Zheng,L.Gao,Z.Gao.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics.Proceedingsofthe46thIEEEConference on Decision and Control,2007:4090–4095.

[21]S.Faetti,P.Grigolini.Unitary point of view on the puzzling problem of nonlinear systems driven by colored noise.Physical Review A,1987,36(1):441–444.

[22]Y.Jia,X.Zheng,X.Hu,et al.Effects of colored noise on stochastic resonance in a bistable system subjectto multiplicative and additive noise.Physical Review E,2001,63(3):DOI 10.1103/PhysRevE.63.031107.

[23]Z.Huang,W.Zhu,Y.Ni,et al.Stochastic averaging of strongly non-linear oscillators under bounded noise excitation.Journal of Sound and Vibration,2002,254(2):245–267.

[24]M.Misono,T.Kohmoto,Y.Fukuda,et al.Stochastic resonance in an optical bistable system driven by colored noise.Optics Communications,1998,152(4/6):255–258.

[25]S.Zhong,H.Xin.Effects of colored noise on internal stochastic resonance in a chemical model system.Chemical Physics Letters,2001,333(1/2):133–138.

[26]B.Guo,Z.Wu,H.Zhou.Active disturbance rejection control approach to output-feedback stabilization of a class of uncertain nonlinear systems subject to stochastic disturbance.IEEE Transactions on Automatic Control,2016,61(6):1613–1618.

[27]D.J.Higham.An algorithmic introduction to numericalsimulation of stochastic differential equations.SIAM Review,2001,43(3):525–546.

[28]Z.Zhao,B.Guo.On active disturbance rejection control for nonlinear systems using time-varying gain.European Journal of Control,2015,23:62–70.