Yet another tutorial of disturbance observer:robust stabilization and recovery of nominal performance

Hyungbo SHIM,Gyunghoon PARK ,Youngjun JOO ,Juhoon BACK ,Nam Hoon JO

1.ASRI,Department of Electrical and Computer Engineering,Seoul National University,Korea;

2.Department of Electrical Engineering and Computer Science,University of Central Florida,U.S.A.;

3.School of Robotics,Kwangwoon University,Korea;

4.Department of Electrical Engineering,Soongsil University,Korea

1 Introduction

Robust control via disturbance observer(DOB)has many advantages over other robust control methods.In particular,it is an inner-loop controller and its primary role isjustto compensate uncertainty in the plantand external disturbances into the plant,so that the inner-loop behaves like a nominal plant without disturbances and uncertainties.Therefore,any outer-loop controller that is designed just for the nominal plant without considering robustness should work,and this enables modular design of controllers;that is,the outer-loop controller deals with nominal stability and nominal performance,and the inner-loop DOB cares forrobustness againstun-certainty and disturbances.In this sense,DOB is in contrast to other robust control methods such as H∞control,adaptive control,or sliding mode control,and there is much design freedom for the outer-loop controller in DOB-based robustcontrol.When there isno uncertainty and disturbance,the DOB-based robust control shows the best nominal performance without intervention of the inner-loop DOB,while the performance degrades gradually as the amount of uncertainty and disturbance grows.Finally,DOB has the benefit of design simplicity(while its theoretical analysis is not simple)so that it has been employed in many industrial applications.

Because of the benefits,a large number of research works have been reported in the literature,including survey-style papers[1–3],monographs[4,5],and related papers[6–9]under the name of “active disturbance rejection control(ADRC)”.On the other hand,this paper presents yet another tutorial of DOB as a summary of recent findings by the authors,in less formalstyle(forexample,we avoid the theorem-proofstyle of writing).We view the DOB1The origin of DOB,which was called a load torque estimator,dates back to[10].It was more or less an estimator rather than a robust controller.as an output feedback robust controller which,under certain conditions such as minimum-phaseness ofthe plantand large bandwidth of the Q-filters,enables robust stabilization against arbitrarily large parametric uncertainty(as long as the uncertain parameters are bounded and their bounds are known a priori),and recovery of nominal steady-state and transient performance.This perspective will lead us to the underlying principles of the DOB that has large bandwidth of Q-filters.

2 System description for analysis

The systems dealt with in this paper are the singleinput-single-output linear time-invariant systems given by

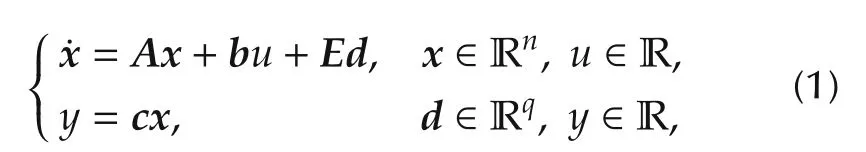
whereuis the input,yis the output,xis the state,anddis the external disturbance.The disturbance signald(t)is assumed to be smooth(i.e.,differentiable as many times as necessary with respect to timet),and we assume thatd(t)and its derivatives are uniformly bounded.The matricesA,b,c,andEare of appropriate sizes,and are assumed to be uncertain.In particular,we assume that system(1)(without the disturbance termEd)is a minimal realization of the transfer function

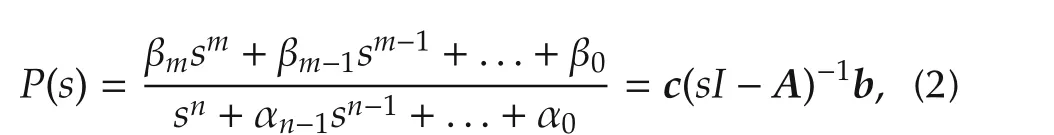
in which,all parameters αiand βiare uncertain,but βm?0 and the sign of βm(which is so-called the highfrequency gain ofP(s))is known.System(1)can always be transformed to

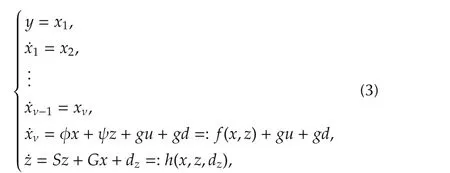
where ν :=n-m,x=[x1···xν]T∈ Rν,andz∈ Rm.Here,the notationfandhare defined for convenience,which will be used frequently later.The disturbance signalsdanddzare linear combinations ofdand its derivatives(for details,refer to the appendix,e.g.,equation(a1)).All the matrices φ ∈ R1×ν,ψ ∈ R1×m,g∈ R1×1,S∈ Rm×m,andG∈ Rm×νare uncertain,but the sign ofgis known andg?0(this is becausegis in fact βm,which is clarified in the appendix).Refer to the appendix for the derivation from(1)to(3).If the plant has the inputdisturbance only(like in Fig.1),then the plantcan be written as in(3)without the termdzin thez-subsystem.

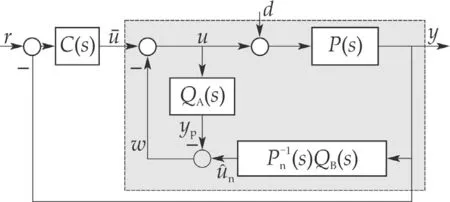
Fig.1 The closed-loop system with DOB structure;r is a reference signal,and d is an input disturbance.The DOB can also be combined with C(s)when implemented,which becomes then a feedback controller having two inputs r and y.

The representation(3)is called thenormal form[11,12]2It is the name of the structure like the well-known controllability/observability canonical form of the plant.The representation(3)of the transfer function(2)can also be directly derived.See[12,p.513–514]for this procedure.By this procedure,it is also seen that,in a certain coordinate,the term Gx in(3)can depend only on x1,so that,Gx can be written like Gx=G?x1=G?y..The reason for writing the system state in the split form ofxandzis to emphasize their different roles that will be seen shortly.The integer ν is called therelative degreeof the plant.It is emphasized that the eigenvalues of the matrixSare the zeros ofP(s)in(2)(see the appendix for the proof),and˙z=Szis called thezero dynamicsof the system.Then,we say the system is ofminimum phaseif and only if the matrixSis Hurwitz.For designing DOB,it is not necessary to convert the given plant into the normal form.The representation(3)is just for the analysis in this paper.

3 Required action for DOB

The behavior of(3)is unexpected because the plantP(s)is uncertain,and thus,the quantities φ,ψ,g,G,andSare consequently uncertain.Hence,one may want to design a control inputusuch that system(3)behaves like its nominal plant:

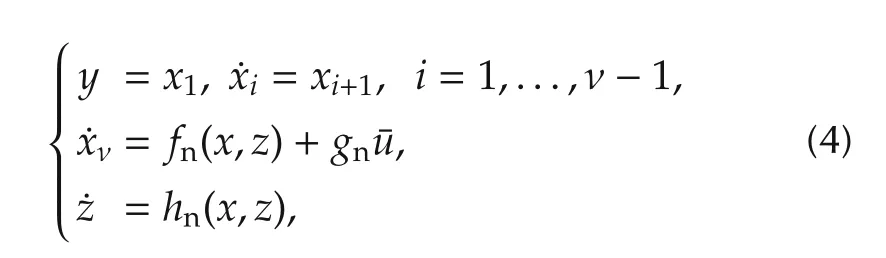
where¯uis an external input that is designed by another(outer-loop)controller.Comparing(3)and(4),it is seen that system(4)is system(3),in which,there is no disturbance and the uncertainf,g,andhare replaced with their nominalfn,gn,andhn,respectively,wherefn(x,z)=φnx+ψnzandhn(x,z)=Snz+Gnx.While the replacement offandgcan be achieved if the controluin(3)becomes the same as

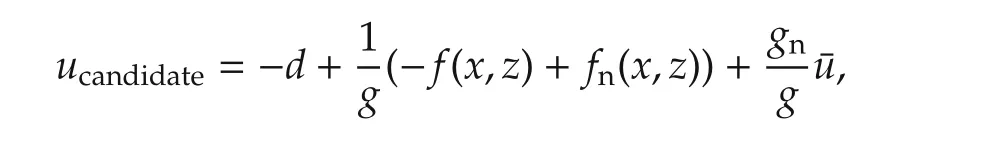
the replacement ofhis a difficult task because thez-subsystem is not directly affected by the controlu.Hence,instead of replacinghin thez-subsystem of(3),let us introduce a new statezn∈Rm(which will be implemented in the controller)and construct a new(dynamic)desired input as

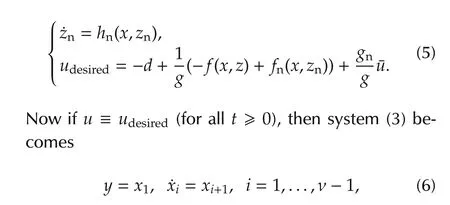
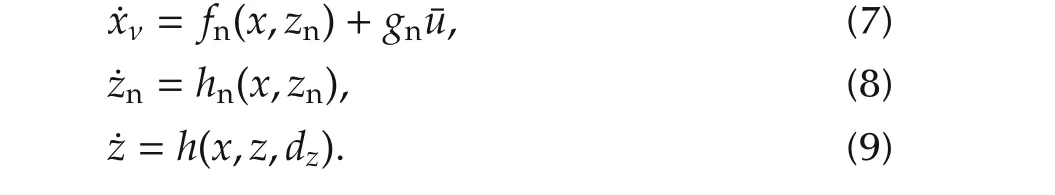
Clearly,system(6)–(8)yields the same behavior as(4).At the same time,thez-subsystem(9)becomes standalone and does not affect the outputy.In other words,the statez,which was observable fromyin(3),has now become unobservable by the desired inputudesired3This is not possible in practice because u desired contains unknown quantities and so we cannot let u≡u desired.However,since the DOB will estimate u desired and let u≈u desired,the degree of observability of z at least gets weakened..This is the cost to pay for enforcing the nominal inputoutput behavior of(4),or(6)–(8),upon the real plant(3).Since we do not have any information ofzfrom the outputy(when this nominal input-output behavior is achieved)and have no more freedom left in the inputu(=udesired)to control thez-subsystem,we have to ask that thez-subsystem is stable itself(i.e.,Sis Hurwitz)so that the statez(t)does not diverge under boundedxanddz.

In order to implement the control idea discussed so far,there are still two more challenges.First,to implement(5),the statexneeds to be estimated becausexis not directly measured but is used to compute the nominal values offn(x,zn)andhn(x,zn).This problem may be solved by a state observer,but arobustestimation ofxis necessary since system(3)is uncertain and is affected by disturbances.Second,sinceudesiredcontains unknown quantities such asd,f(x,z),andg,we cannot compute it directly.Instead,we have to estimateudesired(t)and driveu(t)to the estimate.

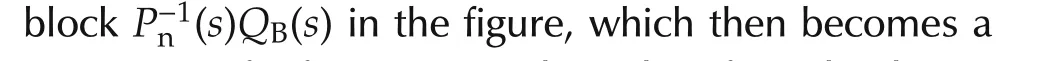
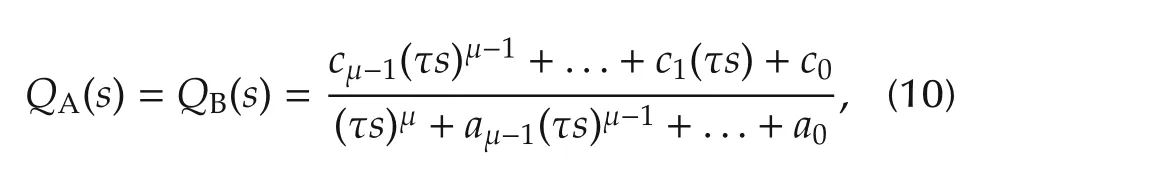
4 A closer look at conventional DOB

For simplicity of presentation,let us consider,from now on,a general example of a third order uncertain plant with relative degree ν=2(i.e.,n=3 andm=1)in(2),and its nominal model

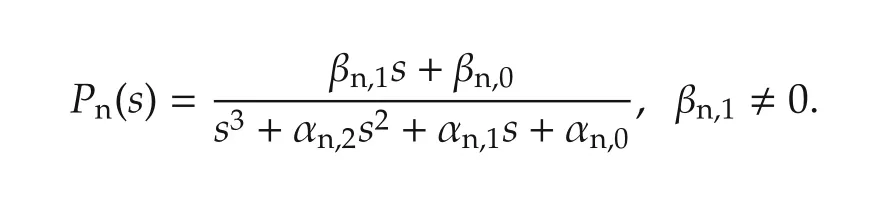
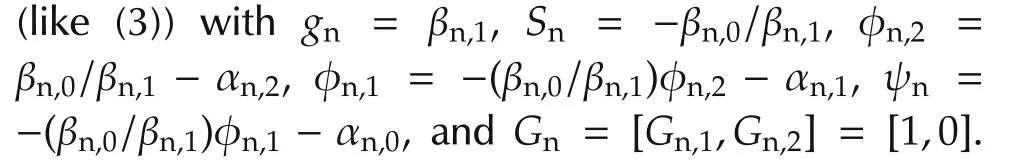
This nominal model has the normal form realization Suppose that the Q-filter has the same relative degree asPn(s)and is taken as

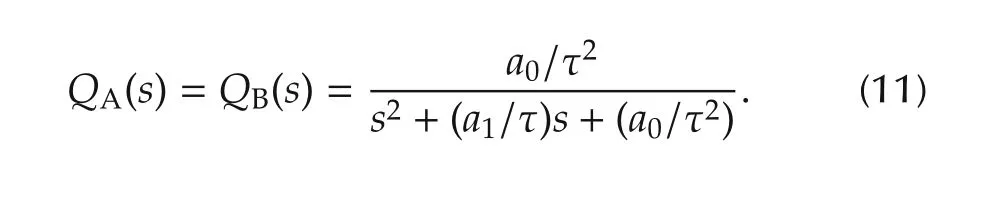
A realization of the filterQA(s)(in Fig.1)is obtained by

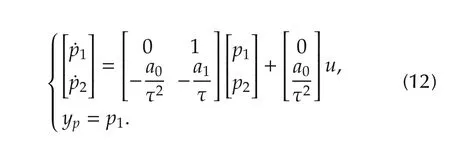
On the other hand,the transfer function

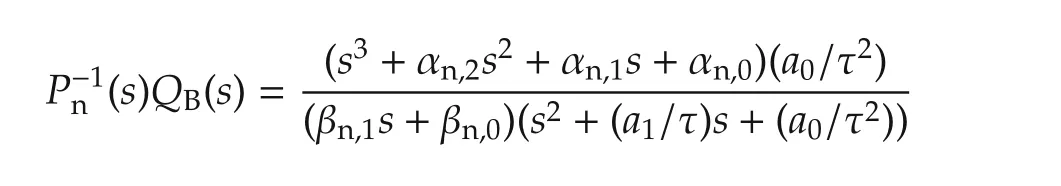
in Fig.1 can be realized as5Assuming that P n(s)is realized as in(4)with the inputu n and the output v,the inverse P-1n(s)can be written as(because x1 is the output and x2 is the derivative of the output)

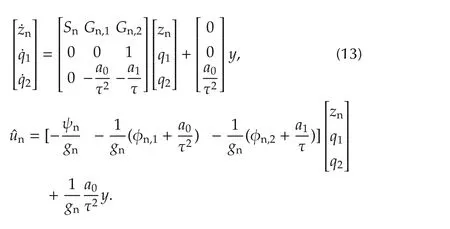
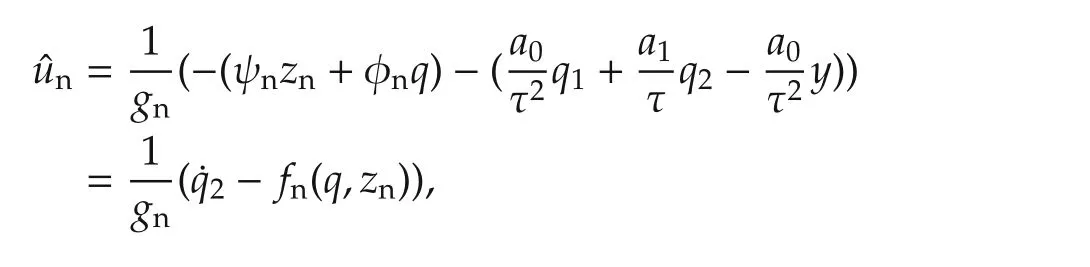
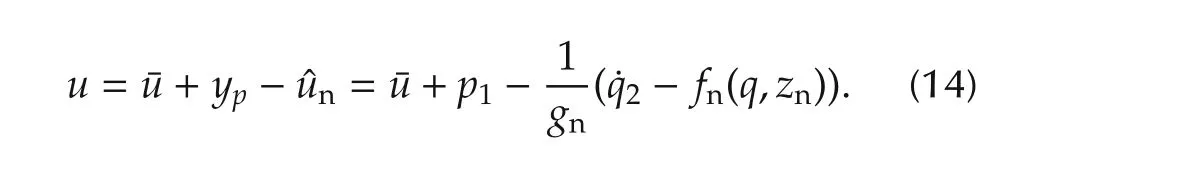
With this,we claim two findings.

4.1 Robust observer is embedded in

It is seen that equation(13)is a cascade of two subsystems

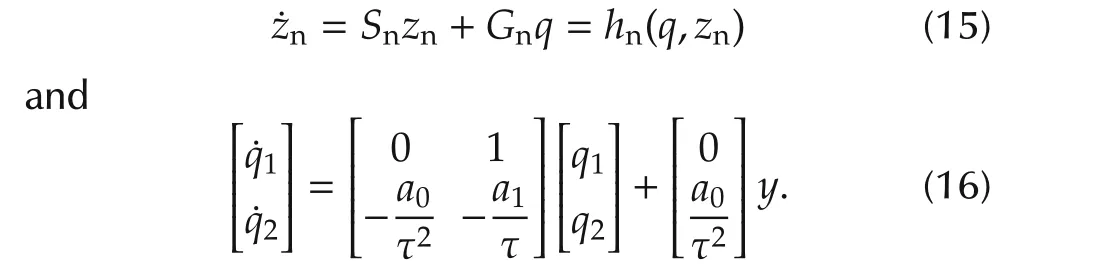
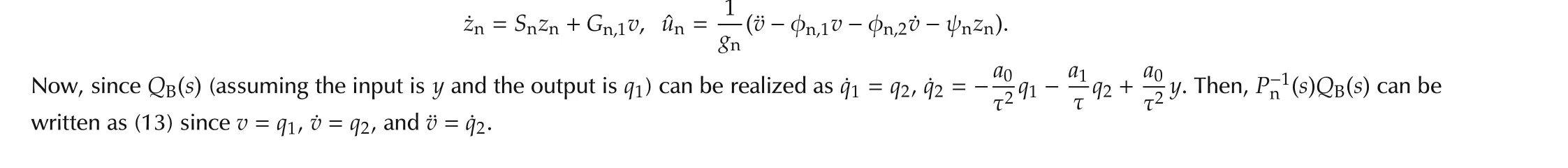
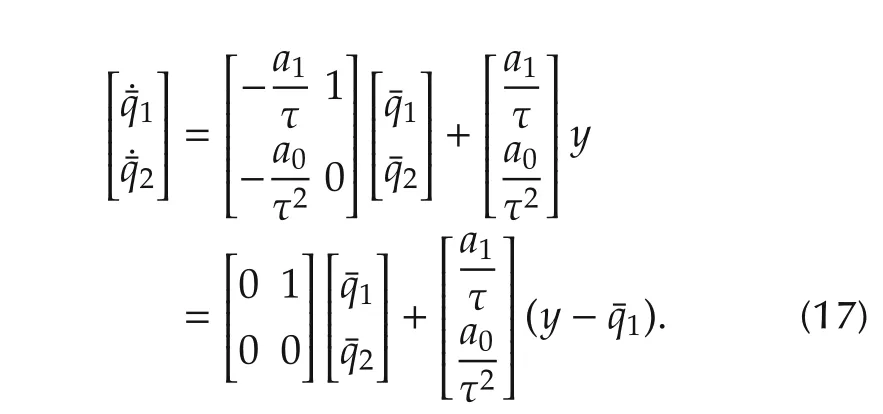
This is the very form of thehigh-gain robust observerforx(but not forz),studied in[15]and many others.According to[15],the state¯q(t)approaches close tox(t)∈ R2of(3)when τ is sufficiently small(so the name“high-gain”follows,as seen in(17)).This is true even though the observer has no information about system(3)(so it is arobustobserver),and the residual error between¯q(t)andx(t)(whenttends to infinity)becomes smaller as τ gets smaller[15].Moreover,from the transformation between¯qandq,we see that(q(t)-¯q(t))→0 as τ → 0.This is the underlying reason whyq(t)can be used as the estimate ofx(t)when the bandwidth of the Q-filter is large(i.e.,τ is small).Onceq(t)is used instead ofx(t),we revisit(15)and see that it is nothing but(5)withxreplaced with its estimate.Verily,the nominalzsubsystem(5)is implemented in the part of controller,

4.2 Estimation of u desired is performed by Q A(s)

In the previous subsection,it is seen thatq(t)→x(t)approximately.Now,in order to have the propertyu(t)→udesired(t),we expect from equation(14)that

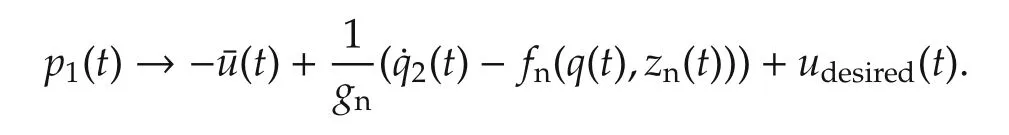
We claim that,if τ is small andaiandciare suitably chosen,then this is the case.

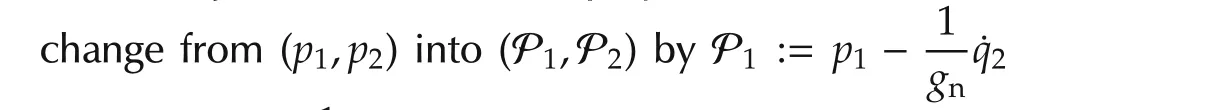
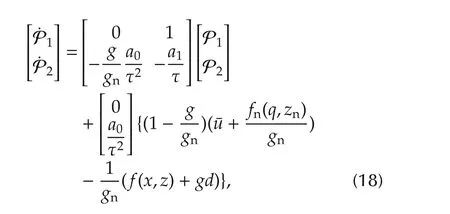
The issue here is that the input term is not constant but a time-varying signal.Nevertheless,if P-dynamics is much faster than this input signal,then the assumption of constant input holds approximately in the relatively fasttime scale,and P1(t)quickly converges to its desired(time-varying)value approximately.This approximation becomes more and more accurate as P-dynamics gets faster(See[12,Section 9.6]forrigoroustreatmentofthis statement).A way to make P-dynamics faster is to take smaller τ,which is seen from the location of eigenvalues(One may argue that,by taking smaller τ,the evolution of the high-gain observer stateq(t)gets also faster that is contained in the input term.While this is true,the stateq(t)quickly converges to the relatively slowx(t),and after that,the input term becomes relatively slowly varying7The argument here is not very rigorous,but just delivers underlying intuition.See[14,17]for more precise proofs using the singular perturbation theory[12].).

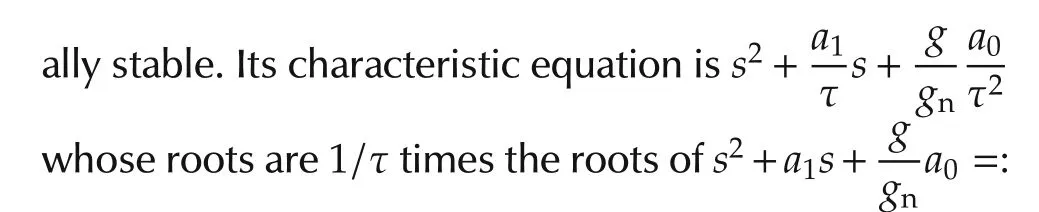
Finally,let us inspect whether system(18)is actu-Pf(s),and thus,stability of(18)is determined by the polynomialPf(s).Sinceg?0 and the sign ofgis known,by letting the nominal valuegnhave the same sign,the polynomialPf(s)is Hurwitz(becausea0＞0 anda1＞0 from the stability of the Q-filter).This is simple because the Q-filter(and thus,the polynomialPf(s))is just of second order.However,if a higher order Q-filter,like(10),is employed,thenPf(s)becomes more complicated(see[16])as

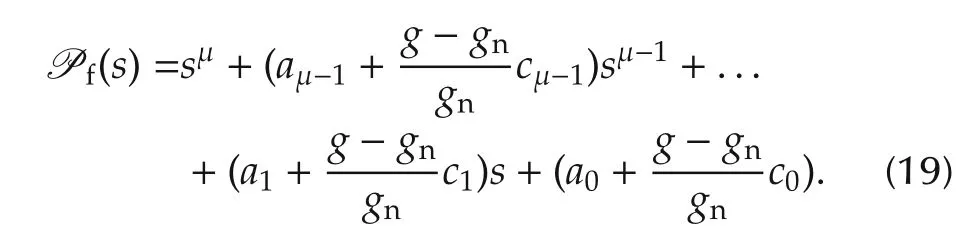
Then it is not straightforward to ensure thatPf(s)is Hurwitz for all variation ofg,and for this,the coefficientsaiandcishould be carefully designed.This observation has been made in[14,16,17].Fortunately,a design procedure ofaiandcihas been developed which makesPf(s)remain Hurwitz for arbitrarily large variation ofgas long as the upper and lower bounds ofgare known.See[18,19]for the general case,but,for making this paper self-contained,we now quote from[16,17]how to chooseaiwhen μ = ν,c0=a0,andci=0 fori=1,...,μ-1(this selection in fact applies to any plant having relative degree ν).In this case,we havePf(s)=sν+aν-1sν-1+...+a1s+(g/gn)a0.First,chooseaν-1,...,a1so that ρ(s):=sν-1+aν-1sν-2+...+a1is Hurwitz.Then,find¯k＞0 such thatsρ(s)+k=sν+aν-1sν-1+...+a1s+kis Hurwitz for all 0＜k?¯k.Such¯kalways exists.Indeed,consider the root locus of the transfer function 1/(sρ(s))with the gain parameterk.Since the root locus includes all points in the complex plane along the real axis to the left of an odd number of poles and zeros(from the right)of the transfer function,and since 1/(sρ(s))has no zeros and has all poles in the left-half plane except one at the origin,the root locus starting at the origin moves to the left as the gainkincreasesa littlefrom zero,while the others remain in the open left-half plane for thesmallvariation ofkfrom zero.The closed-loop of the transfer function 1/(sρ(s))and the gainkhas its characteristic equationsρ(s)+k,and this implies the existence of(possibly small)¯k＞0.With such¯kat hand,now choosea0=¯k/max{g/gn}where the maximum is known whilegis uncertain(therefore,a0often tends to be small).For the general case,this idea is repeatedly applied.

At last,we note that,if the variation ofgis small so thatg≈gn,then the termg-gnmay be almost zero so thatPf(s)remains Hurwitz for allgsince the Q-filter is stable so thatsμ+aμ-1sμ-1+...+a0itself is Hurwitz.Therefore,with small uncertainties,the stability issue ofPf(s)does not stand out andPf(s)is automatically Hurwitz.

5 Robust stability of DOB-based control system

From the discussions so far,we know that,with HurwitzPf(s)and small τ,the high-gain observer subsystem(16)or(17)and the subsystem(18)are stable.It is however not enough for the stability of the overall closed-loop system,and let us take the outer-loop controllerC(s)into account as well.Inspecting robust stability of the overall system with DOB is indeed not an easy task in general.To see the extent of difficulty,let us expressP(s)=N(s)/D(s),Pn(s)=Nn(s)/Dn(s),QA(s)=Na(s)/Da(s),QB(s)=Nb(s)/Db(s),andC(s)=Nc(s)/Dc(s)where all“N”and “D”stand for numerator and denominator coprime polynomials,respectively.Then,the overall system in Fig.1 is stable if and only if the characteristic polynomial(we omit“(s)”for convenience)

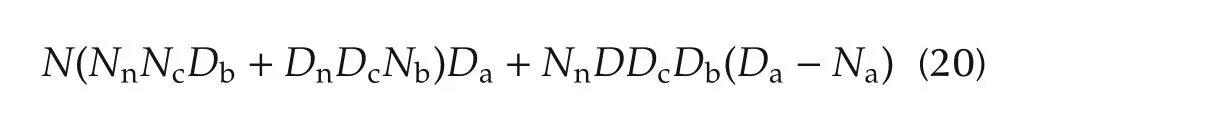
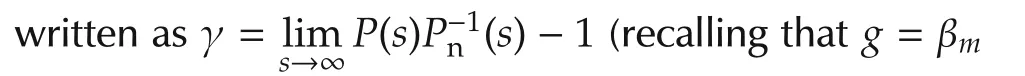
Since the roots of the characteristic polynomial(20)approach the roots of(21)and 1/τ times the roots of(22)as τ → 0,robust stability of the overall feedback system is guaranteed if

A)N(s)is Hurwitz(i.e.,thez-subsystem of(3)is stable),

B)DnDc+NnNcis Hurwitz(i.e.,C(s)internally stabilizesPn(s)(notP(s))),

C)Pf(s)remains Hurwitz forallvariationsofg(=βm),and if the bandwidth of Q-filter is sufficiently large(i.e.,τ is sufficiently small).If any root of(21)or(22)appears in the open right-half complex plane,then the overall system becomes unstable with large bandwidth of Q-filter.Therefore,the above conditions A)–C)are necessary and sufficient for robust stability of DOB-based control systems under sufficiently large bandwidth of Q-filters,except the case when any root of(21)or(22)has zero real part because,in this case,it is not clear in which direction the roots of(20)approach the roots of(21)and 1/τ times the roots of(22).

It is again emphasized that one group of roots have more and more negative real parts as τ → 0(when(22)is Hurwitz),and this confirms that some part inside the overall system operates faster than other parts.This observation goes along with the previous discussions in the state-space(Section 4).Another way to appreciate(21)and(22)is the following.The polynomial(22)corresponds to the dynamics which governs the behaviorthatu(t)→udesired(t)while(21)determines the behavior whenu(t)=udesired(t).Indeed,whenu(t)=udesired(t),thez-subsystem becomes stand-alone and the uncertain termsfandgare replaced withfnandgnso that stability ofz-subsystem(orN(s))and stability of the nominal closed-loop(orDn(s)Dc(s)+Nn(s)Nc(s))are required.

6 Robust transient response

For some industrial applications,robust transient response(in addition to robust steady-state response)is very important.For example,if a controller has been designed to satisfy some time-domain specifications such as rising time,overshoot,and settling time for a nominal plant model,then it is desired that the same transient performance is maintained for the real plant under disturbances and uncertainties.By“robust transient response”,we mean that the output trajectoryy(t)of the real plant remains close to the outputynominal(t)for all t?0(i.e.,from the initial time)under disturbances and uncertainties,whereynominal(t)is supposed to be the output of the nominal closed-loop system(with the same initial condition).How can we achieve robust transient response?In order fory(t)of(3)to be the same asynominal(t)for allt?0,we have to havey(i)(t)=y(i)nominal(t)fori=0,1,...,ν.This task is achieved ifu(t)=udesired(t)for allt?08If u(t)=u desired(t)from the initial time t=0,then the outer-loop controller C(s)feels as if the initial condition of the plant is(x(0),z n(0))(not(x(0),z(0))).To see this,refer to(6)–(9).,Therefore,the signalynominal(t)should be understood as the nominal output resulted by the interaction betweenC(s)and the nominal plant(6)–(8),which is actually the action required for the DOB9There are two more approaches in the literature to achieve robust transient response(while the underlying principle that u(t)→u desired(t)quickly is the same).One is the universal controller of[28]with high-gain observer.This is much similar to DOB,but there is no inner loop of Q A(s)in Fig.1(which yields 1/(1-Q A(s))).Instead,its role is played by a large static gain.The other one is the L1 adaptive control of[29,30],for which a constructive design method of the controller still lacks though..In fact,this is another reason whyu(t)should convergequicklytoudesired(t).Itis indeed because,ifu(t)converges toudesired(t)rather slowly,then the time interval fory(ν)(t)?y(ν)nominal(t)becomes large and therefore,even afteru(t)converges toudesired(t),two signalsy(t)andynominal(t)are already different and so afterward.

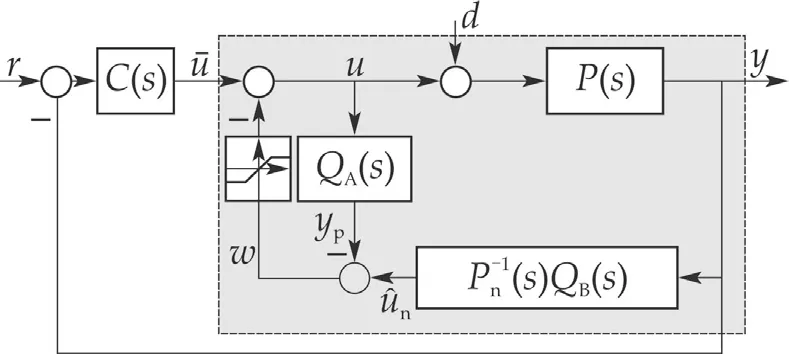
Fig.2 DOB structure with saturation for robust transient response.

7 Extensions

The analysis of this paper allows more extensions as follows.

·Nonlinear plant:The analysis of the previous sections also applies to single-input-single-outputnonlinear plants as long as they have well-defined relative degree so that the plant can be represented as in the normal form like(3)10See[11]about how to transform a nonlinear system with well-defined relative degree into the normal form..See[17]for more details.

·MIMO plant:Multi-input-multi-output plants also admit the DOB.See[23]for details.

·Reduced-order DOB:Since the same Q-filters are found in Fig.1,they could be merged into one in order to reduce the dimension of the DOB.See[24,25].

·Exact(not approximate)rejection of disturbances:Nominal performance recovery(or disturbance rejection)studied in this paper is based on the convergenceu→udesired.This convergence,however,is inherently approximate because estimation ofudesired(t)is approximate and the convergence ofu(t)to the estimate ofudesired(t)is also approximate,although the approximation becomes more and more accurate as τ gets smaller.However,if the disturbance is generated by a known generating model(which is called anexosystem),then exact rejection of the disturbance,without relying on smallness of τ,is possible(One typical example is the sinusoidal disturbance with known frequency).The tool used for this purpose is the well-knowninternal model principle[26],and the controllerdesign has been studied under the name ofoutput regulationin,e.g.,[27].The DOB(more specifically,the Q-filters)can be modified to include the generating model of the disturbance,so that the internal model principle holds for the closed-loop system.The initialresultin this direction is found in[31].For embedding the generating model of sinusoidal disturbance with robust stabilization,refer to[18,19,32].

·Different Q-filters:The conventional DOB consists of two same Q-filters,while their roles are inherently different as discovered in Section 4.Such observation has triggered subsequent works[20,32,33]in which the Q-filters are refined separately for certain purposes.For instance,since the estimation ofudesired(t)is mainly performed byQA(s),it is sufficient to embed the generating model of disturbance just intoQA(s)(but not intoQB(s))for the exact disturbance rejection[32].Another example is to use higher order ofQB(s)(while the order ofQA(s)being kept the same)in order to have more reduction of the effect of measurement noise[33].

·Use of state feedback controllerC:Since the estimate of the plant’s statexis provided by the DOB,the outer-loop controllerCcan be of state feedback type if the full state is considered as(x,zn)whereznis also provided by the DOB.See[34]for this combination.

·Input saturation:In practice,it is natural that the control inputuis limited.A preliminary result on DOB-based controller under input saturation has been reported in[35],where the authors presented an LMI to find the control gain for a state feedback controller and the parameters of DOB at the same time.

·Discrete-time implementation of DOB:While all the above results are discussed in the continuous-time domain,for implementing the DOB in the digital devices,DOB is constructed in the discrete-time domain.At first glance,stability seems to remain guaranteed if the continuous-time DOB is discretized by fast sampling.However,fast sampling(with zero-order hold)of a continuous-time system introduces additional zeros(which are calledsampling zeros[36,37]),and worse yet,at least one of them is always unstable when the relative degree ν?3.This causes another trouble that the sampled-data model of the plant becomes a nonminimum phase system,which seems violating the nec-essary condition forstability as discussed earlier.In[38],it has been found that the Q-filters in the discrete-time domain can be specially designed to take care of unstable sampling zeros as well while maintaining all good properties in the continuous-time domain.

8 Restrictions

We have so far looked at the conventional DOB and its extensions,and found thatthe DOB is a powerfultool for robust control and disturbance rejection.These benefits came under the requirement that the bandwidth of the Q-filter is sufficiently large,and this in turn imposed a few restrictions as follows.

·Unmodelled dynamics:If there is unmodelled dynamics in the real plant,then the relative degree ν of the plantP(s)may be different from that of the nominal modelPn(s).In this case,it has been actually reported in[39]that large bandwidth may lead to instability of the overall system,even though a remedy for a few cases is also suggested in[39].See also[40].

·Non-minimum phase plant:If the real plant is of non-minimum phase(i.e.,the zero dynamics is unstable),then large bandwidth of Q-filters makes the overall system unstable,as discussed before.To overcome this restriction,another structure with different Q-filters has been proposed in[41],but the problem is still open in general.

·Sign of high frequency gain:We have seen that the sign of the(uncertain)high-frequency gaing(or βm)should be known.If it is not the case,then,as a workaround,the Nussbaum gain technique[42]has been employed in[43],while more study is called for in this direction.

·Measurement noise:Large bandwidth of Q-filters may also yield insufficient reduction of noise at high frequencies while we refer to[33,44,45]for a possible modification of the DOB structure to enhance the noise reduction capability.

We emphasize that,if the bandwidth of Q-filter is severely limited by some reason,then the desired steady-state/transient performance and the robust stabilization may not be obtained simply because the analysis so far is no longer valid.Fortunately,an appropriate bandwidth of Q-filter for robust stabilization and disturbance rejection,varies from system to system,and it turns out that the bandwidth of Q-filter need not be too large in many practical cases.For instance,a reasonable choice of bandwidth worked in the experiments of[46,47].The analysis in the related papers yields an upper bound for τ that works,in theory.However,since it is often too conservative,finding suitable τ is done usually by repeated simulations or by tuning it in experiments.

On the otherhand,there are otherapproaches thatdo not explicitly rely on large bandwidth of Q-filter for robust stability[3,48–55].Among them,the most popular one is to employ the tool“small-gain theorem”[51–53].However,it gives a sufficient condition for stability and so may yield conservatism.More specifically,for an uncertain plant with multiplicative uncertainty(i.e.,P(s)=Pn(s)(1+ Δ(s))where Δ(s)is an unknown stable transfer function),the condition for robust stability is derived as?Δ?s=jω＜ ?(1+PnC)/(Q+PnC)?s=jωfor all ω[53].Then,the size of uncertainty is severely limited(considering the typical case 0??Q?s=jω?1).

Another one is working with thestate(not output)measurements as in[1,56,57].On the other hand,assuming that the disturbance is an output of a generating model(the exosystem),the disturbance observers which estimate the disturbance by estimating the exosystem’s state,are often proposed and combined with many wellestablished controllers such as sliding mode control or model predictive control.See,for example,[4,5]for more details.

In spite of these restrictions,study of DOB under large bandwidth of Q-filters is worthwhile since it illustrates the role of each component of DOB,and yields useful insights for further study of DOB.It also shows ideal performance that can be achieved under arbitrarily large parametric uncertainty and disturbances,and constructive design guides of Q-filters are derived.

Finally,we close this tutorial with a disclaimer that the purpose of this tutorial is not to survey exhaustive list of related contributions on DOB,but just to present a new perspective of the authors about the DOB.Therefore,some important contributions on DOB may have been omitted.This tutorial is written in less formal manner,and more rigorous,theorem-proof style,arguments can be found in the references cited in the text.

[1]L.Guo,W.Chen.Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach.International Journal of Robust and Nonlinear Control,2005,15(3):109–125.

[2]W.Chen,J.Yang,L.Guo,et al.Disturbance observer-based control and related methods:an overview.IEEE Transactions onIndustrial Electronics,2016,63(2):1083–1095.

[3]E.Sariyildiz,K.Ohnishi.A guide to design disturbance observer.Journal of Dynamic Systems,Measurement,and Control,2014,136(2):DOI 10.1115/1.4025801.

[4]L.Guo,S.Cao.Anti-disturbanceControlforSystemswithMultiple Disturbances.Boca Raton:CRC Press,2013.

[5]S.Li,J.Yang,W.Chen,etal.DisturbanceObserver-basedControl:Methods and Applications.Boca Raton:CRC Press,2014.

[6]G.Tian,Z.Gao.From Poncelet’s invariance principle to active disturbance rejection.Proceedings of the American Control Conference,New York:IEEE,2009:2451–2457.

[7]Z.Gao.Active disturbance rejection control:from an enduring idea to an emerging technology.Proceedings of the 10th International Workshop on Robot Motion and Control,Poznan:IEEE,2015:269–282.

[8]Z.Gao.On the centrality of disturbance rejection in automatic control.ISA Transactions,2014,53(4):850–857.

[9]W.Xue,Y.Huang.Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems.ISA Transactions,2015,58:133–154.

[10]K.Ohishi,K.Ohnishi,K.Miyachi.Torque-speed regulation of DC motor based on load torque estimation method.Proceedings of JIEE International Power Electronics Conference,Tokyo,1983:1209–1218.

[11]A.Isidori.Nonlinear Control Systems.3rd ed.Berlin:Springer,1995.

[12]H.K.Khalil.NonlinearSystems.3rd ed.Englewood Cliffs:Prentice Hall,2002.

[13]K.Kong,M.Tomizuka.Nominal model manipulation for enhancement of stability robustness for disturbance observerbased control systems.InternationalJournalofControl,Automation and Systems,2013,11(1):12–20.

[14]H.Shim,Y.Joo.State space analysis ofdisturbance observerand a robust stability condition.Proceedings of Conference on Decision and Control,New Orleans:IEEE,2007:2193–2198.

[15]H.K.Khalil,L.Praly.High-gain observers in nonlinear feedback control.International Journal of Robust and Nonlinear Control,2014,24(6):993–1015.

[16]H.Shim,N.H.Jo.An almostnecessary and sufficientcondition for robuststability ofclosed-loop systems with disturbance observer.Automatica,2009,45(1):296–299.

[17]J.Back,H.Shim.Adding robustness to nominal output-feedback controllers for uncertain nonlinear systems:a nonlinear version of disturbance observer.Automatica,2008,44(10):2528–2537.

[18]G.Park,Y.Joo,H.Shim,et al.Rejection of polynomial-in-time disturbances via disturbance observer with guaranteed robust stability.Proceedings of Conference on Decision and Control),Maui:IEEE,2012:949–954.

[19]Y.Joo,G.Park,J.Back,et al.Embedding internal model in disturbance observer with robust stability.IEEE Transactions on Automatic Control,2016:10.1109/TAC.2015.2503559.

[20]Y.Joo,G.Park.Reduced order type-k disturbance observer based on generalized Q-filter design scheme.Proceedings ofInternational Conference on Control,Automation and Systems,Korea,2014:1211–1216.

[21]H.J.Sussmann,P.V.Kokotovic.The peaking phenomenon and the global stabilization of nonlinear systems.IEEE Transactions on Automatic Control,1991,36(4):424–440.

[22]F.Esfandiari,H.K.Khalil.Output feedback stabilization of fully linearizable systems.International Journal Control,1992,56(5):1007–1037.

[23]J.Back,H.Shim.An inner-loop controller guaranteeing robust transient performance for uncertain MIMO nonlinear systems.IEEE Transactions on Automatic Control,2009,54(7):1601–1607.

[24]J.Back,H.Shim.Reduced-order implementation of disturbance observers for robust tracking of non-linear systems.IET Control Theory&Applications,2014,8(17):1940–1948.

[25]J.Back,H.Shim.Robust tracking by reduced-order disturbance observer:Linear case.Proceedings of Joint Conference on DecisionandControlandEuropeanControlConference,Orlando:IEEE,2011:3514–3519.

[26]B.A.Francis,W.M.Wonham.The internal model principle of control theory.Automatica,1976,12(5):457–465.

[27]J.Huang.Nonlinear Output Regulation:Theory and Applications.New York:SIAM,2004.

[28]L.B.Freidovich,H.K.Khalil.Performance recovery of feedbacklinearization-based designs.IEEE Transactions on Automatic Control,2008,53(10):2324–2334.

[29]K.K.K.Kim,E.Kharisov,N.Hovakimyan.Filter design for L1adaptive output-feedback controller.Proceedings of Joint Conference on Decision and Control and European Control Conference,Orlando:IEEE,2011:5653–5658.

[30]C.Cao,N.Hovakimyan.L1adaptive output feedback controller to systems of unknown dimension.Proceedings of the American Control Conference,New York:IEEE,2007:1191–1196.

[31]K.Yamada,S.Komada,M.Ishida,et al.Characteristics of servo system using high order disturbance observer.Proceedings of Conference on Decision and Control,Kobe:IEEE,1996:3252–3257.

[32]G.Park,Y.Joo,H.Shim.Asymptotic rejection of sinusoidal disturbances with recovered nominal transient performance for uncertain linear systems.Proceedings of Conference on Decision and Control,Los Angeles:IEEE,2014:4404–4409.

[33]J.Han,H.Kim,Y.Joo,et al.A simple noise reduction disturbance observer and Q-filter design for internal stability.Proceedings of International Conference on Control,Automation and Systems,Gwangju:IEEE,2013:755–760.

[34]J.Ha.Design of Nonlinear Disturbance Observer for State Feedback Based Control.Master thesis.Seoul:Seoul National University,2014(in Korean).

[35]M.C.Yoon,J.S.Kim,J.Back.Robust stabilization of constrained uncertain linear systems using feedforward control based on high-gain disturbance observer.Proceedings of International Conference on Control,Automation and Systems,Busan:IEEE,2015:290–294.

[36]K.J.Åstr¨om,P.Hagander,J.Sternby.Zeros of sampled systems,Automatica,1984,20(1):31–38.

[37]J.I.Yuz,G.C.Goodwin.Sampled-data Models for Linear and Nonlinear Systems.3rd ed.Berlin:Springer,2014.

[38]G.Park,Y.Joo,C.Lee,et al.On robust stability of disturbance observer for sampled-data systems under fast sampling:an almost necessary and sufficient condition.Proceedings of Conference on Decision and Control,Osaka:IEEE,2015:7536–7541.

[39]N.H.Jo,Y.Joo,H.Shim.A study of disturbance observers with unknown relative degree of the plant.Automatica,2014,50(6):1730–1734.

[40]N.H.Jo,Y.Joo,H.Shim.Can a fast disturbance observer work under unmodeled actuators?Proceedings of International Conference on Control,Automation and Systems,Gyeonggi-do:IEEE,2011:561–566.

[41]N.H.Jo,H.Shim,Y.I.Son.Disturbance observer for nonminimum phase linear systems.International Journal of Control,Automation and Systems,2010,8(5):994–1002.

[42]R.D.Nussbaum.Some remarks on a conjecture in parameter adaptive control,Systems&Control Letters,1983,3(5):243–246.

[43]H.J.Yoon.Design of Disturbance Observer with Unknown Input Gain Sign.Master thesis.Seoul:Seoul National University,2012(in Korean).

[44]W.Xie.High frequency measurement noise rejection based on disturbance observer.Journal of the Franklin Institute,2010,347(10):1825–1836.

[45]N.H.Jo,H.Shim.Robust stabilization via disturbance observer with noise reduction.Proceedings of European Control Conference,Switzerland,2013:2861–2866.

[46]J.Yi,S.Chang,Y.Shen.Disturbance-observer-based hysteresis compensation forpiezoelectric actuators.IEEE/ASMETransactions on Mechatronics,2009,14(4):456–464.

[47]J.S.Bang,H.Shim,S.K.Park,et al.Robust tracking and vibration suppression for a two-inertia system by combining backstepping approach with disturbance observer.IEEE Transactions on Industrial Electronics,2010,57(9):3197–3206.

[48]E.Schrijver,J.Van Dijk.Disturbance observers for rigid mechanical systems:Equivalence,stability,and design.Journal of Dynamic Systems,Measurement,and Control,2002,124(4):539–548.

[49]R.Bickel,M.Tomizuka.Passivity-based versus disturbance observer based robot control:Equivalence and stability.Journal of Dynamic Systems,Measurement,and Control,1999,121(1):41–47.

[50]E.Sariyildiz,K.Ohnishi.Bandwidth constraints of disturbance observer in the presence of real parametric uncertainties.European Journal of Control,2013,19(3):199–205.

[51]C.J.Kempf,S.Kobayashi.Disturbance observer and feedforward design for a high-speed direct-drive positioning table.IEEE Transactions on Control Systems Technology,1999,7(5):513–526.

[52]B.A.Guvenc,L.Guvenc.Robust two degree-of-freedom addon controller design for automatic steering.IEEE Transactions on Control Systems Technology,2002,10(1):137–148.

[53]K.S.Eom,I.H.Suh,W.K.Chung.Disturbance observer based path tracking control of robot manipulator considering torque saturation.IEEE/ASMETransactionsonMechatronics,2001,11(3):325–343.

[54]Y.Choi,K.Yang,W.K.Chung,et al.On the robustness and performance of disturbance observers for second-order systems.IEEE Transactions on Automatic Control,2003,48(2):315–320.

[55]C.-C.Wang,M.Tomizuka.Design of robustly stable disturbance observers based on closed loop consideration using H∞optimization and its applications to motion control systems.ProceedingsoftheAmericanControlConference,New York:IEEE,2004:3764–3769.

[56]W.Chen.Disturbance observer based control for nonlinear systems.IEEE/ASME Transactions on Mechatronics,2004,9(4):706–710.

[57]K.-S.Kim,K.-H.Rew,S.Kim.Disturbance observer for estimating higher order disturbances in time series expansion.IEEE Transactions on Automatic Control,2010,55(8):1905–1911.

[58]C.Chen.Linear System Theory and Design.3rd ed.Oxford:Oxford University Press,1999.

Appendix

The conversion from(1)to(3)is done by the following procedure.First,it is noted thatcAi-1b=0 fori=1,...,ν-1 andcAν-1b?0,which is because the relative degree ofP(s)is ν=n-mso that the inputudoes not appear explicitly until we take time derivative ofyup to ν times(This is again becauseP(s)remains strictly proper until we multiply it bysν).Then,the row vectorscAi-1fori=1,...,ν are linearly independent.Indeed,it is seen that

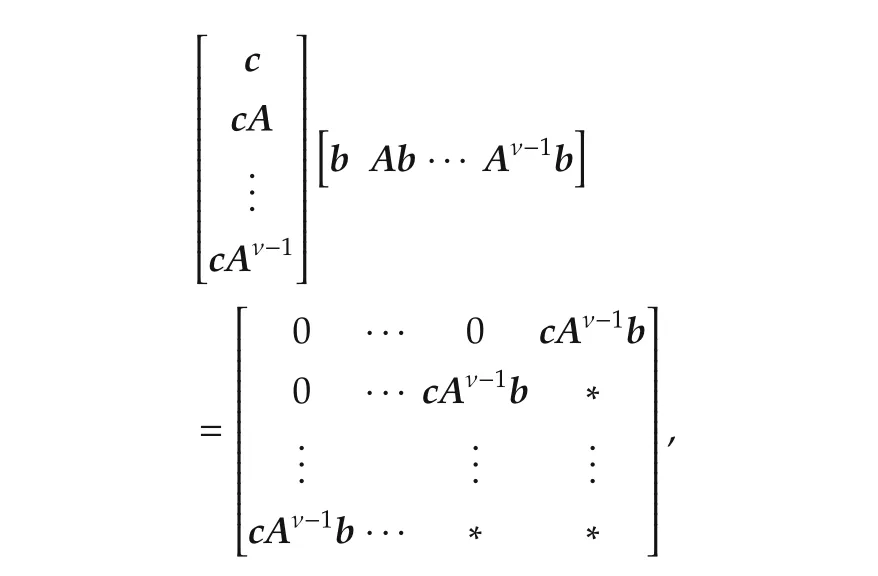
from which,two matrices on the left-hand side have full row/column ranks.Then,one can easily find a matrixΦ ∈ Rm×nsuch that Indeed,the dimension of the left nullspace ofbisn-1,and from the derivation,it is clear thatcAν-1does not belong to the left nullspace ofbwhile ν-1 vectorscAi-1,i=1,...,ν-1,belong to it.Therefore,one can find(n-1)-(ν-1)=mlinearly independent row vectors in the subspace that are linearly independent ofcAi-1,i=1,...,ν-1.

Now,let

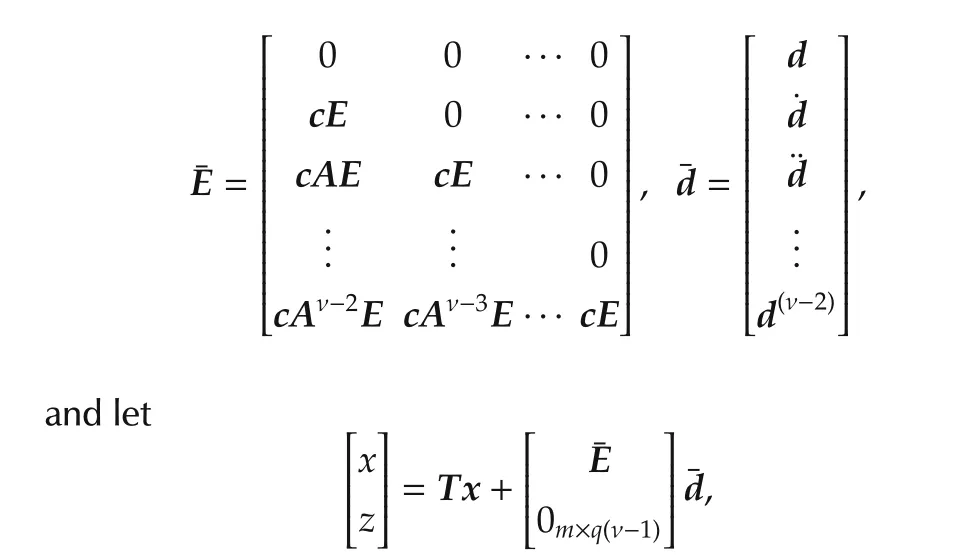
wherex∈Rνandz∈Rm.For convenience,letT-1=:[Ta,Tb]withTa∈ Rn×νandTb∈ Rn×m.Then,it can be seen that system(3)is obtained.Indeed,we verify that

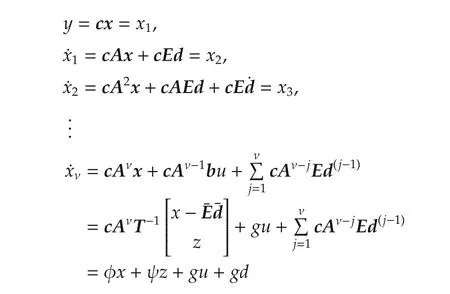
by lettingg=cAν-1b11g is in fact βm in(2).Indeed,from(2),we have that sνP(s)= βm+(a strictly proper transfer function).This implies that y(ν)= βm u+...,and from this,it is clear that g=βm.,φ =cAνTa,ψ =cAνTb,and

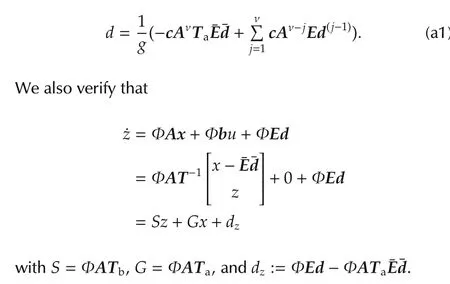
It is noted that,if there is no disturbance,then the conversion from(1)to(3)is nothing but the similarity transformation by the matrixT.Therefore,the poles and zeros ofP(s)are preserved both in(1)and(3).While it is clear that the eigenvalues of the system matrix of(3)are the poles,it is important to note that the eigenvalues ofSare the zeros of the system.Indeed,let λ¯z=S¯zwith λ and¯zbeing the eigenvalue and the eigenvector ofS,respectively.Then,the following equality holds:

in which,the left matrix is the Rosenbrock system matrix[58]of(3).The above equation implies that the Rosenbrock matrix loses rank with λ,and thus,the value λ is the zero of the system[58].