On ADRC for non-minimum phase systems:canonical form selection and stability conditions

Wenchao XUE ,Yi HUANG ,Zhiqiang GAO

1.Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China;

2.Department of Electrical and Computer Engineering,Cleveland State University,Cleveland,Ohio 44115,U.S.A.

1 Introduction

As is well known,uncertainties rejection is one of the fundamental issues in automatic control.The controllerrejector pair,proposed by[1],presents a generic principle for control structure with two degrees of freedom(TDOF),i.e.,the controller is designed for the canonical form of plant;the difference between the actual model and the canonical form,deemed as disturbance,is to be estimated and cancelled by the rejector.Also,the novel definition of rejector greatly helps to reorient many observers/estimators to estimate the uncertainties,such as unknown input observer(UIO)[2],proportional integral observer(PIO)[3],disturbance observer(DOB)[4,5],nonlinear disturbance observer(NDOB)[6,7],extended state observer(ESO)[8,9],etc.(see[10–12]).

This paper pays particular attention to the rejector in terms of ESO,which is strikingly featured with estimating the “total disturbance”or the total effect of unmodelled dynamics and disturbance[9,13].In the last two decades,the active disturbance rejection control(ADRC),which suggests to use ESO as a powerful rejector,has been successfully applied to many industrial processes[14]and embedded in the chips of Texas Instrument[15].To effectively deal with multifarious control problems,many modifications on ADRC have also been constructed by combining ESO and other control methods,such as optimalcontrol[16,17],back-stepping control[18],sliding model control[19],adaptive control[20,21],predictive control[22],feedforward controller[23],etc.Nevertheless,they usually share the following TDOF:one designs feedforward/feedback law based on the canonical form of plant to achieve desired outputresponse and the otherone cancels the“totaldisturbance”via the estimation which is timely provided by ESO,as shown in Fig.1.

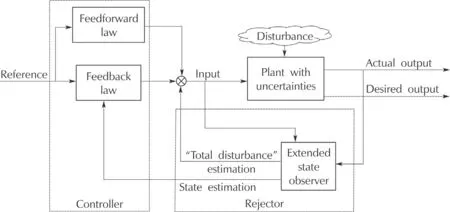
Fig.1 ADRC:ESO based TDOF.

Although the two degrees in ADRC approach have independent tasks,their operations depend on the canonical form which essentially stands for the necessary information of the system to be known.In particular,both desired output and ESO are constructed based on the canonical form selected.Therefore,canonical form is crucial for ADRC.

The canonical form of the systems with no zero dynamics(or zeros for LTI systems)has been well studied for ADRC design[25,26].Moreover,similar canonical form is proven to be effective forsystems with minimum phase which means that the systems have stable zero dynamics[20,27,28].In addition,severaleffective methods have been proposed for ADRC to tackle certain kinds of non-minimum phase systems with the information of zeros being fully known[24,29].However,canonical form selection for the systems which have uncertain and unstable zeros is still an open problem.This paper aims to study the canonical form as well as the corresponding ADRC design for uncertain non-minimum phase systems.Our contributions include that:

?The uncertainties of the systems are shown to be equivalently divided into the two terms in the control channel and the output channel.Correspondingly,the canonical form and the resulting ADRC for the uncertain systems,which could be non-minimum phase,is presented.

?The necessary and sufficient condition for the stability of the closed-loop system with some uncertainties is rigorously studied.Also,the necessity of the detectability of the extended system and certain information ofthe system’s“zeros”,indicates the fundamental guideline in designing and tuning ADRC.

The paper is organized as follows.We introduce the basic idea of ADRC in Section 2.In Section 3,we present the canonical form as well as the ADRC controller for a class of uncertain systems.In Section 4,the stability condition of the closed-loop system is rigorously studied.Section 5 is the simulation study and the last section is devoted to conclusions.

2 Basic idea of ADRC

First,the following class of uncertain systems with the form of cascade of integrators is used to present the basic idea of ADRC,

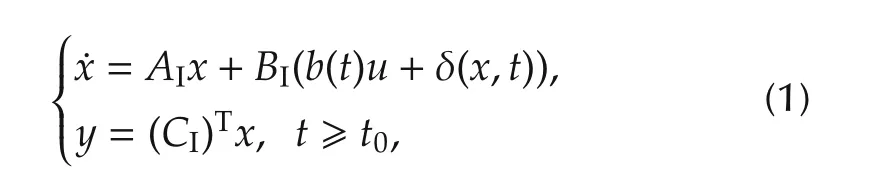
wherex∈Rnis the state vector,y∈R is the output to be regulated,u∈R is the control input to be designed,b(t)is a known and nonzero function,(AI,BI,CI)satisfies

and δ(·)is the “total disturbance”or the total effect of the unknown nonlinear dynamics and external disturbance.

The canonicalform of(1)isusually setasthe following cascade of integrators[25]

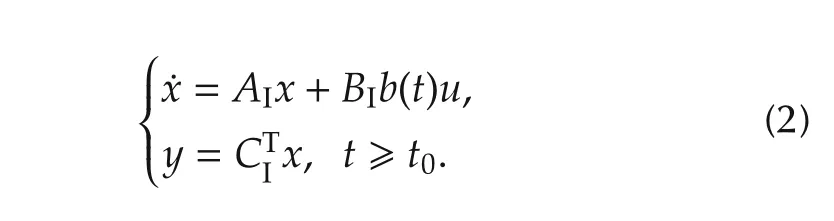
Let the control object be forcingyto approach the desired outputy＊generated by

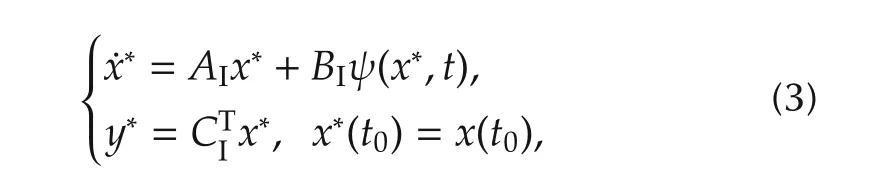
where the function ψ(·)is used to shape the trajectory ofy＊according to practical requirements and conditions,such as the requirements on overshoot,rising time,maximal control input value,etc.

The difference between(1)and(3)implies that bothxand δ(·)are timely needed foryto tracky＊by designingu.ESO suggests to treat δ(·)as an extended state to be estimated,and the linear ESO usually has the form of

is stable and has desired eigenvalues1In this paper,the matrix or transfer function is stable means that all its roots or poles have negative real part..Consequently,the control input becomes

It is straightforward to understand the TDOF in ADRC(4)–(6)for tracky＊,i.e.,

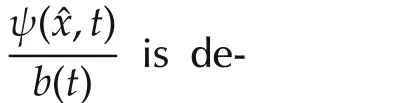
It seems that the controller and the the rejector have independent tasks in(4)–(6).However,both of their structures heavily depend on the canonical form(2).In particular,the control law ψ(·)is constructed based on(2),and the form of ESO(4)also stems from(2).Therefore,canonical form is a critical issue to be addressed for ADRC.Existing literatures have shown that the the canonical form of cascade of integrators is effective for the minimal phase systems[20,26–28].In this paper,we will discuss the canonical form selection for ADRC to deal with the uncertain systems which could be nonminimal phase.

3 Canonical form selection for ADRC

Consider the following class of nonlinear uncertain systems

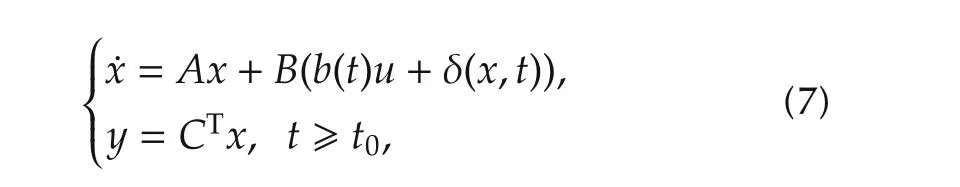
wherex∈Rnis the state vector,y,uandb(t)have the same meanings as those in(1).The matricesA∈ Rn×n,B∈ Rn×1andC∈ Rn×1are assumed to have uncertainties and satisfy the follow typical assumption,

Assumption 1The pair(A,B)is controllable and the pair(A,C)is observable.

Since(A,B,C)has general form,the model(7)can describe both non-minimal phase and minimal phase systems.Next,we will analyze the uncertainties in(7)to present its canonical form.

According to the knowledge of linear system[30],Assumption 1 means that there exists a nonsingular matrixT∈ Rn×nsuch that

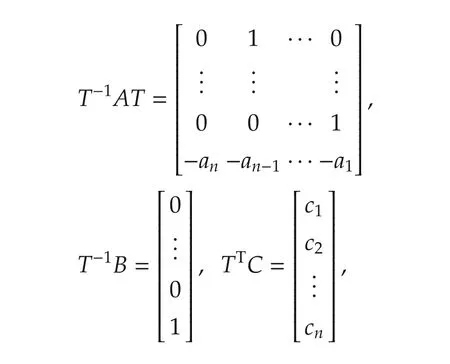
whereaiandci,i=1,...,nare uncertain parameters due to the uncertainties in(A,B,C).The exact form ofTis probably unavailable due to the uncertainties in(A,B,C).Fortunately,from the structure of(T-1AT,T-1B,TTC),both the uncertainties in(A,B,C)and inTcan be included into(ai,ci),i=1,...,n.Next,we assume that¯aiand¯ciare the nominal value or known information ofaiandci,respectively.Consequently,

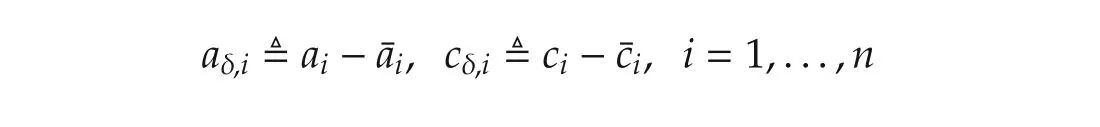
are the unknown parts of the parameters.Furthermore,let¯x?[¯x1¯x2···¯xn]T=Tx,then system(7)can be equivalently written as

include all the uncertainties in system(7)or(8).

Remark 2In the case of¯δ(¯x,t)=0 andCδ=0,it can be verified that the transfer function from the input(b(t)u(t))to the outputy(t)satisfies

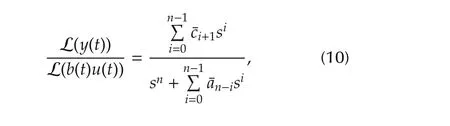
where L is the Laplace operator.Thus,aδ,iandcδ,iactually stand forthe uncertaintiesin the“poles”and“zeros”for system(8),respectively.It is evident that these two groups of uncertainties are contained in¯δ(·)andCδ.Therefore,we will use the form of system(8)instead of(7)in the following analysis such that the physical meanings of uncertain terms are transparent.

Also,consider the desired output¯y＊generated by

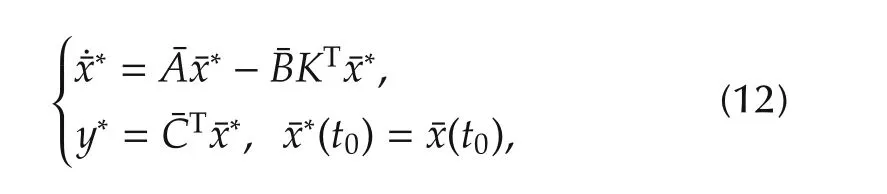
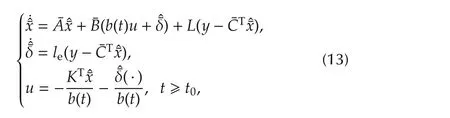
whereL∈Rnandle∈R are parameters to be designed such that(Ae-LeCTe)is stable,where

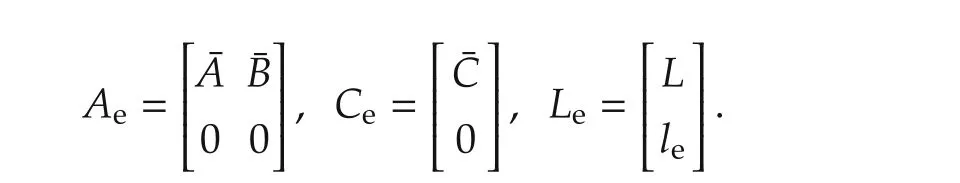
It can be verified that the ADRC based closed-loop system constituted of(8)and(13)satisfies

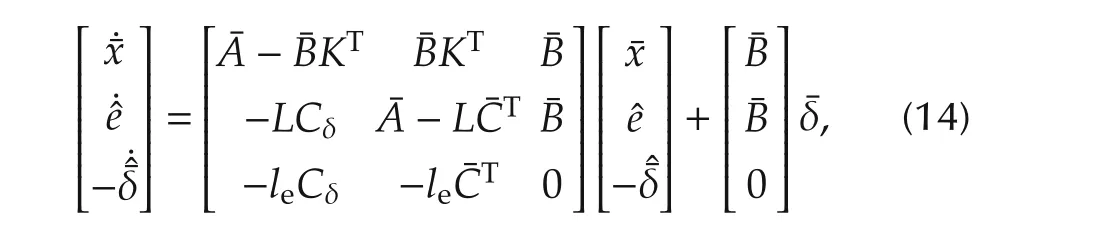
4 Stability conditions for the closed-loop system

First,the assumption for the initial value¯x0is given.

Assumption 2?¯x(t0)??ρ0,where ρ0is positive.Define

then the closed-loop system(14)equals to

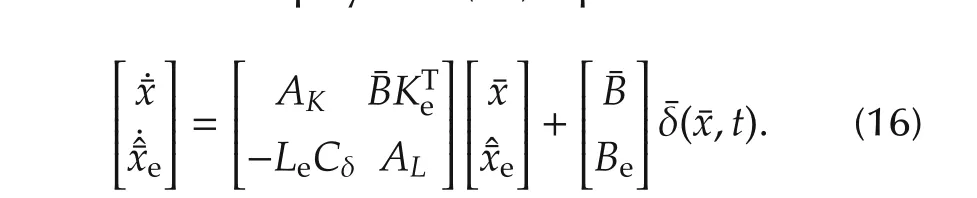
Theorem 1Let Assumptions 1 and 2 be satisfied.There exist nonegatives αi,i=1,2,3 such that

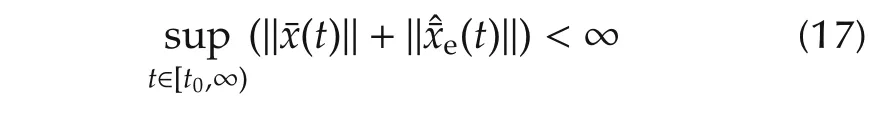
for any|¯δ(¯x,t)|?α1?¯x?+α2and any?Cδ??α3if and only if every root of

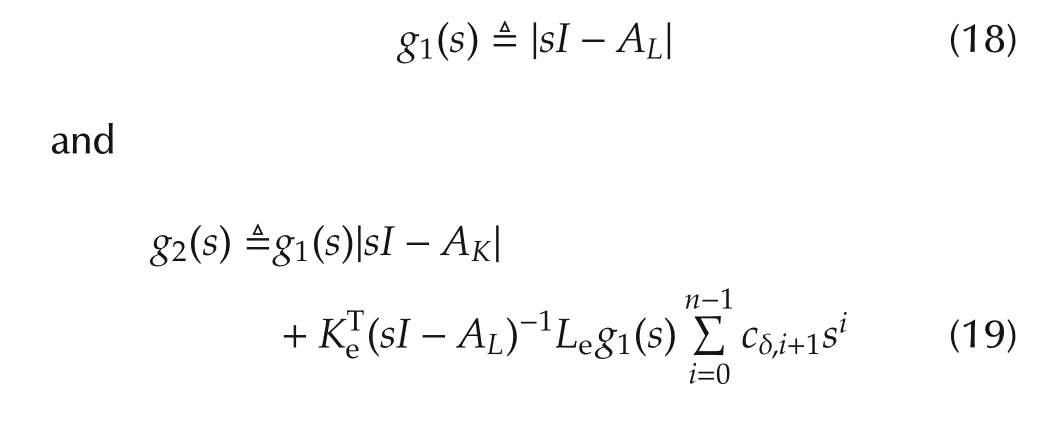
is stable.

Theorem 1 essentially reflects the necessary and sufficient condition for the stability of the ADRC based closed-loop system despite some uncertainties in both¯δ(·)andCδ.Therefore,the applicability of the proposed ADRC(13)can be specified by checking that whether the selected parameters in controller ensure the stability of the roots of(18)and(19).Also,the condition of Theorem 1 indicates the fundamental guideline in designing and tuning ADRC.

Note that Theorem 1 shows the necessary and sufficient condition for the system with the uncertain function¯δ(¯x,t)being bounded by certain linear function,i.e.,|¯δ(¯x,t)|?α1?¯x?+α2,then this condition is also necessary for the system with more general uncertain functions.

Since the gain of ESO,i.e.,Leis a tunable parameter vector,the existence ofLeto ensure the condition given in Theorem 1 needs to be addressed.

Lemma 1There existsLesuch that every root ofg1(s)is stable if and only if the pair(Ae,Ce)is detectable.In addition,(Ae,Ce)is always detectable in the case of¯c1?0.

According to Lemma 1,the detectability of the pair(Ae,Ce)is necessary for the validation of the canonical form(11).We also remark that checking this detectability is straightforward since the matrices(Ae,Ce)are exactly known.Note that system(1)implies that¯c1=1,then the nominal model(11)always makes sense for the systems with cascade of integrators.

We proceed to the discussion for theg2(s)which depends onCδ.SinceCδrepresents the uncertainty in the“zeros”of system(7),the stability of the roots ofg2(s)is used to show how much uncertainty in the “zeros”can be tolerated by the proposed canonical form based ADRC(13).Although the solution for the size ofCδto ensure the stability of the roots ofg2(s)cannot be explicitly obtained,it can be numerically solved under any given(Le,K),as illustrated by the example in Section 5.

Proof of Theorem 1First,the necessary condition for(18)will be proven.Consider the particular case ofCδ=0,δ(·)≡ α2,then there is

Note that?Be??0,then one of the roots ofg1(s)being unstable means that

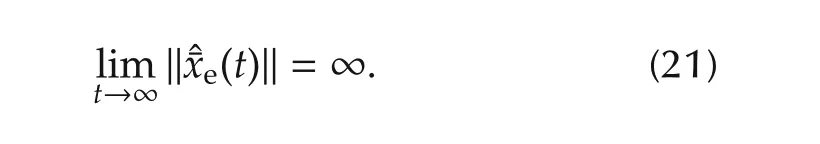
Therefore,the stability of all roots ofg1(s)is necessary.Define

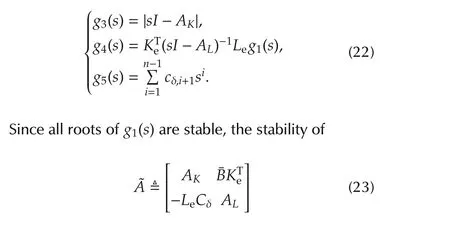
equals to the stability of the roots of

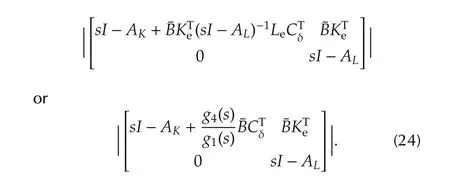
Evidently,the roots of(24)are those ofg1(s)and

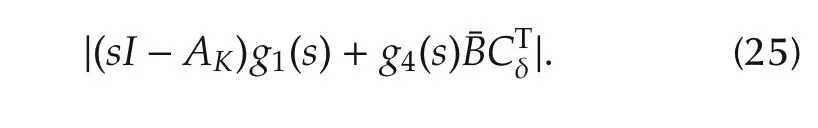
According to the exact form of¯A,¯B,CTδandK,there is

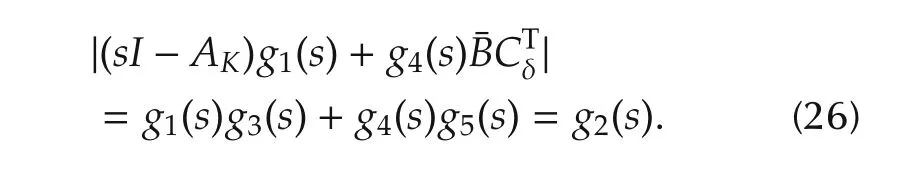
Similar to(20)–(21),the stability of all roots ofg2(s)is also necessary for(17).

Next,the sufficiency condition of(18)–(19)will be proven.According to the analysis between(23)and(26),the stability of(18)–(19)indicates that the matrix˜Ais Hurwitz.Thus,there exists a positive matrix˜Psuch that

for any given α3.Furthermore,it can be verified that there exist positives α1,α2and αsuch that for any|¯δ(¯x,t)|?α1?¯x?+α2,there is

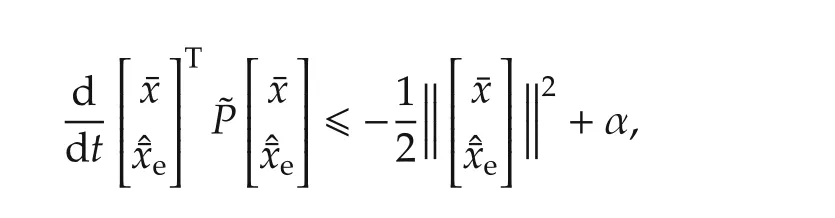
which implies(17). ?

Proof of Lemma 1According to the definition of detectability,detectability of the pair(Ae,Ce)is necessary and sufficient for the existence ofLesuch that every root ofg1(s)is stable.Moreover,there is

which has full rank in case of¯c1?0.Thus,¯c1?0 implies(Ae,Ce)is observable as well as detectable. ?

5 Simulation study

5.1 Example 1

Consider the following 2nd order nonlinear system

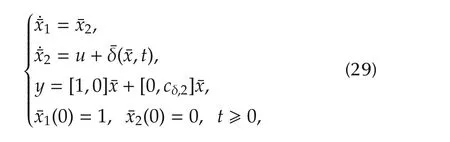
where the uncertain term¯δ(¯x,t)is assumed to satisfy

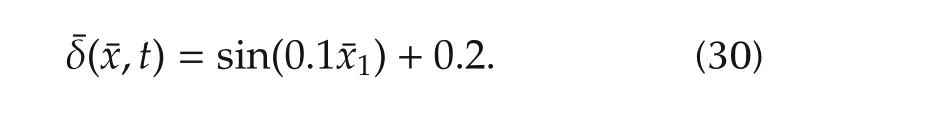
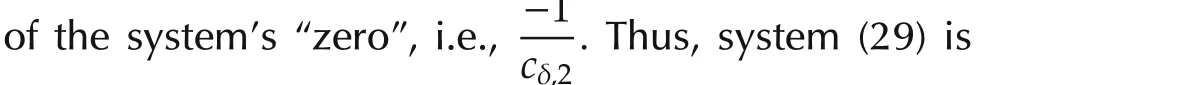
wherel1,l2andleare tuned by the following popular law[31]:

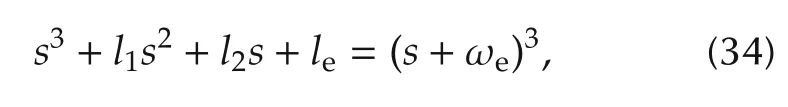
where ωeis the bandwidth of the ESO in(33)and is set by ωe=5.

Fig.2 shows the responses of the corresponding ADRC based closed-loop system with the following cases of the system’s “zero”

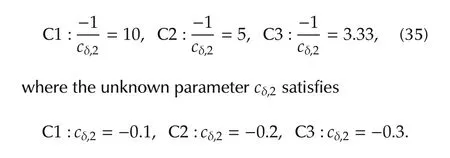
It is evident that the proposed canonical form(31)based ADRC controller(33)can stabilize the closed-loop system with C1 and C2,but it fails with C3.Actually,this can be rigorously explained by Theorem 1 which shows that the stability of the roots of

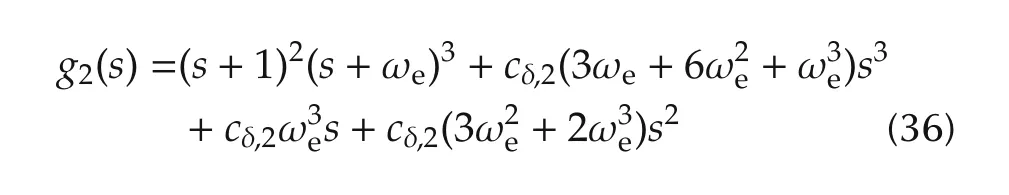
is necessary for the applicability of ADRC(33).Moreover,the minimalcδ,2to ensure the stability ofallroots ofg2(s)can be numerically computed under(ωc=1,ωe=5),as shown in Table 1.It is evident that the minimalcδ,2forthe stability ofallrootsofg2(s)under(ωc=1,ωe=5)is-0.2,which is accordance with the results in Fig.2.

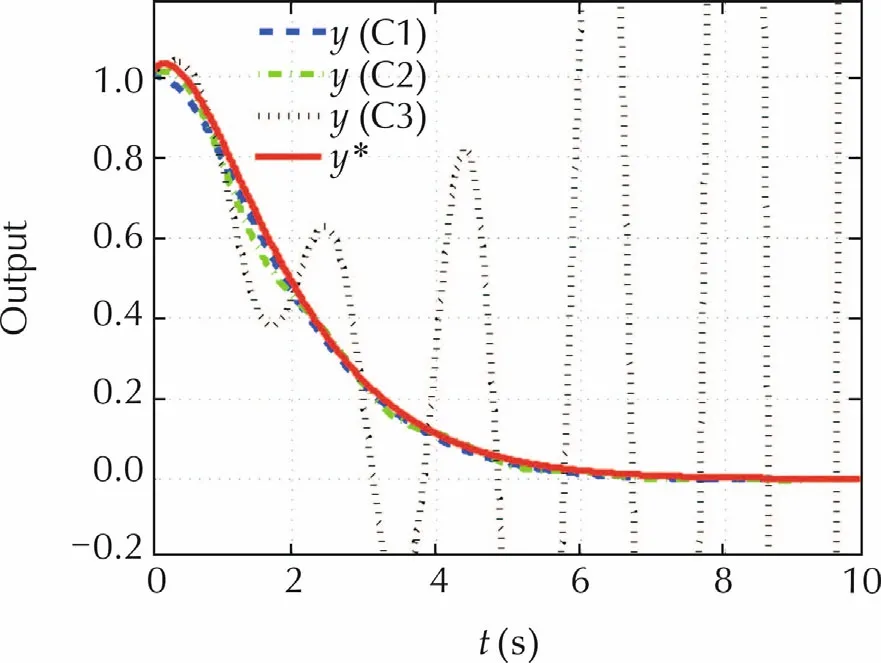
Fig.2 The responses of the closed-loop system with(ωc=1,ωe=5)and ADRC(33).

Remark 3From Table 1,larger ωcor ωeleads to larger positive “zero”or smaller size of the uncertaintycδ,2tolerated by ADRC.Note that large ωcor ωeis usually used for fast tracking reference signal or estimating uncertainties,then smaller uncertainties in the unstable zero is required to achieve better performance of the ADRC based control system.

Table 1 The minimalall roots of g2(s).

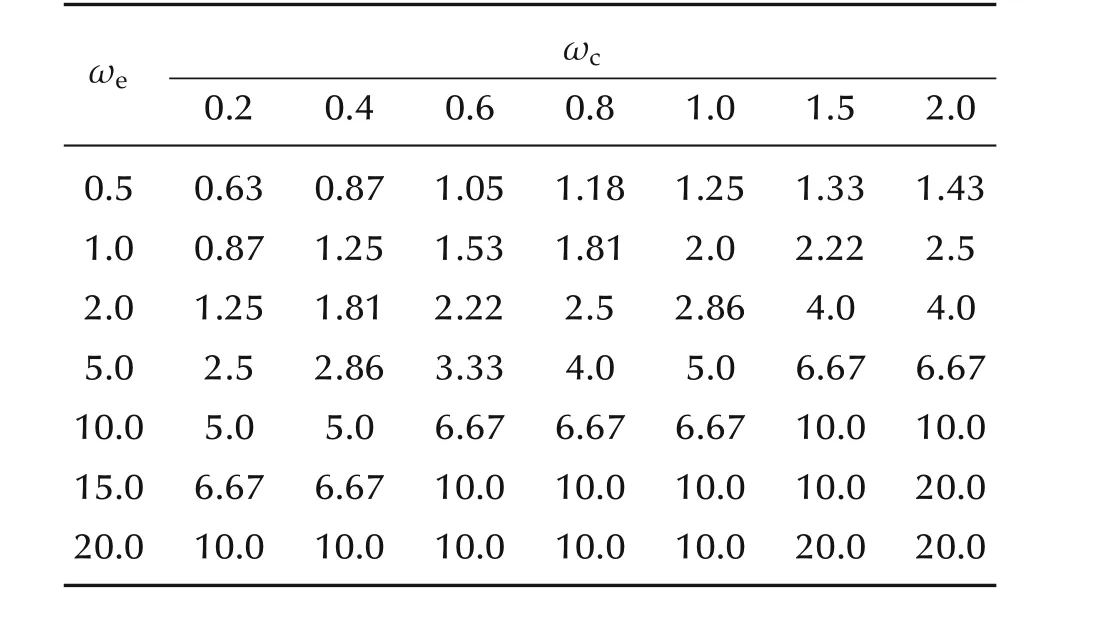
Table 1 The minimalall roots of g2(s).

ωe 0.2 0.4 0.6 0.8 1.0 1.5 2 ωc 0.5 0.63 0.87 1.05 1.18 1.25 1.33 1 1.0 0.87 1.25 1.53 1.81 2.0 2.22 2.0.43.5 2.0 1.25 1.81 2.22 2.5 2.86 4.0 4.0 5.0 2.5 2.86 3.33 4.0 5.0 6.67 6.67 10.0 5.0 5.0 6.67 6.67 6.67 10.0 10.0 15.0 6.67 6.67 10.0 10.0 10.0 10.0 20.0 20.0 10.0 10.0 10.0 10.0 10.0 20.0 20.0

Theorem 1 actually presents the limitation of the ADRC(33)in dealing with the uncertainty in zero.Moreover,it is necessary to known more information of the system’s zero if its location is far more its estimation.In particular,if we known more precise information for the zero of system(29)such that the system is

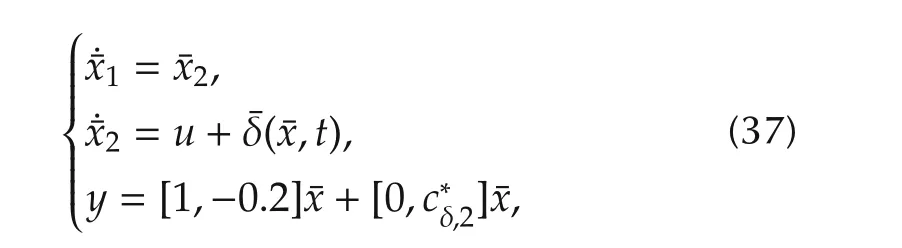
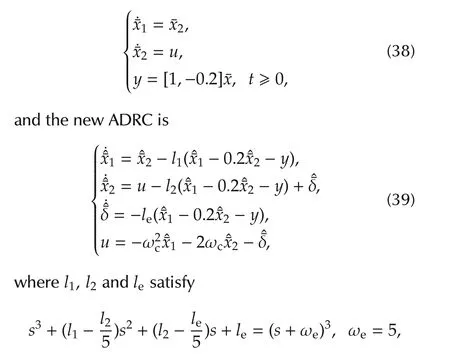
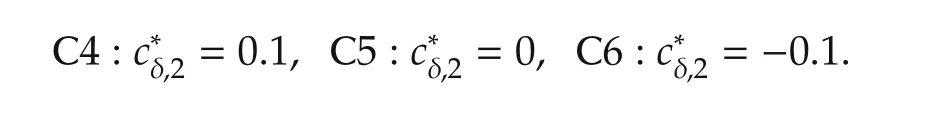
Fig.3 illustrates that the proposed new ADRC controller(39)can stabilize the closed-loop system with the system’s “zero”being

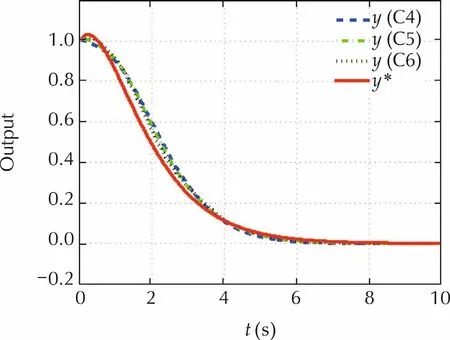
Fig.3 The responses of the closed-loop system with(ωc=1,ωe=5)and ADRC(39).

5.2 Example 2

Consider the following non-minimal phase system in the form of transfer function:

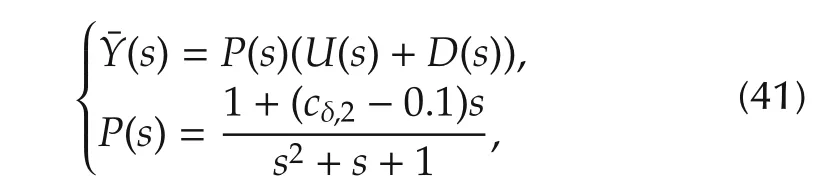
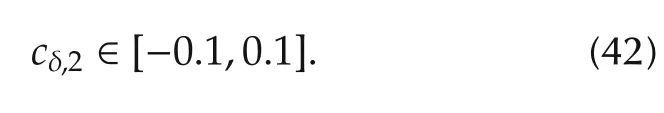
Obviously,cδ,2decides the unknown partofthe system’s zero.Therefore,the nominal model of(41)is

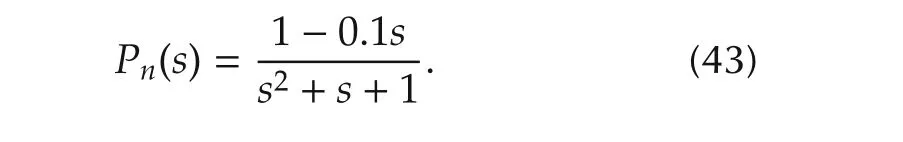
Consequently,the canonical form of system(41)in the state space can be

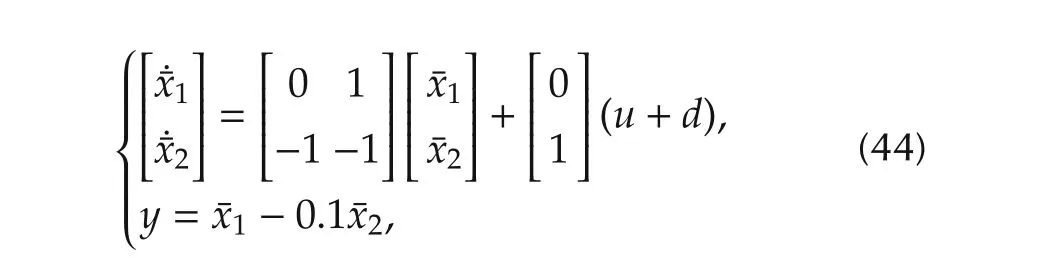
then(13)means that the ESO for system(41)is

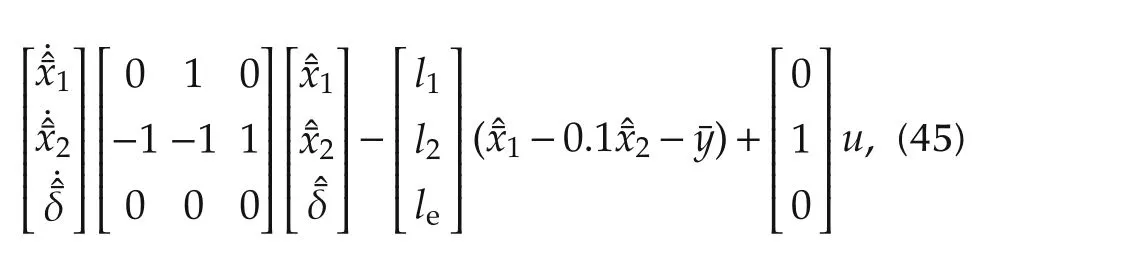
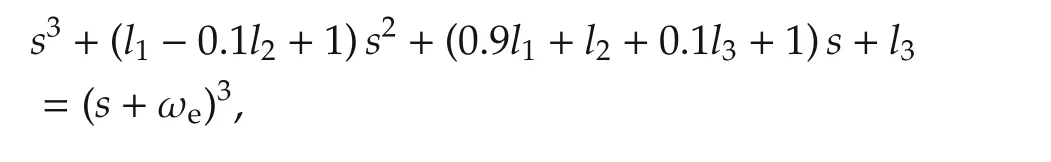
where ωe＞ 0 is the only parameter to be chosen.

Let the desired output¯y＊satisfy

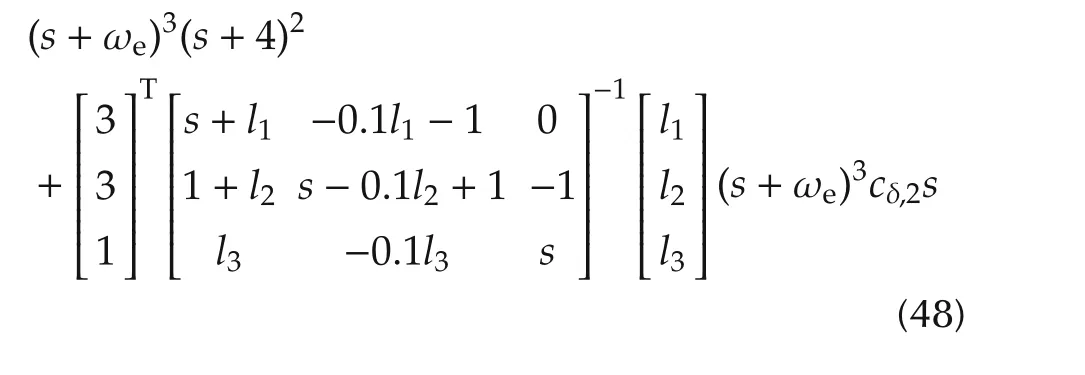
By the results of Theorem 1,the necessary condition for the stability of the closed-loop system with(41),(45)and(47)is that all roots of are stable for∀cδ,2∈ [-0.1,0.1].Actually,this condition requires that ωecannot be set to an arbitrary value,as shown in Fig.4.Also,the numerical computation shows that ωeshould satisfy ωe＜ 14.In Fig.5,the responses of the corresponding closed-loop system are presented under

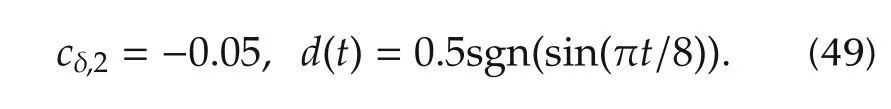
It is obvious that the stability of the closed-loop system is ensured by choosing the ωewhich satisfies ωe＜ 14,and well estimation of the uncertainty is obtained by the proposed ESO.

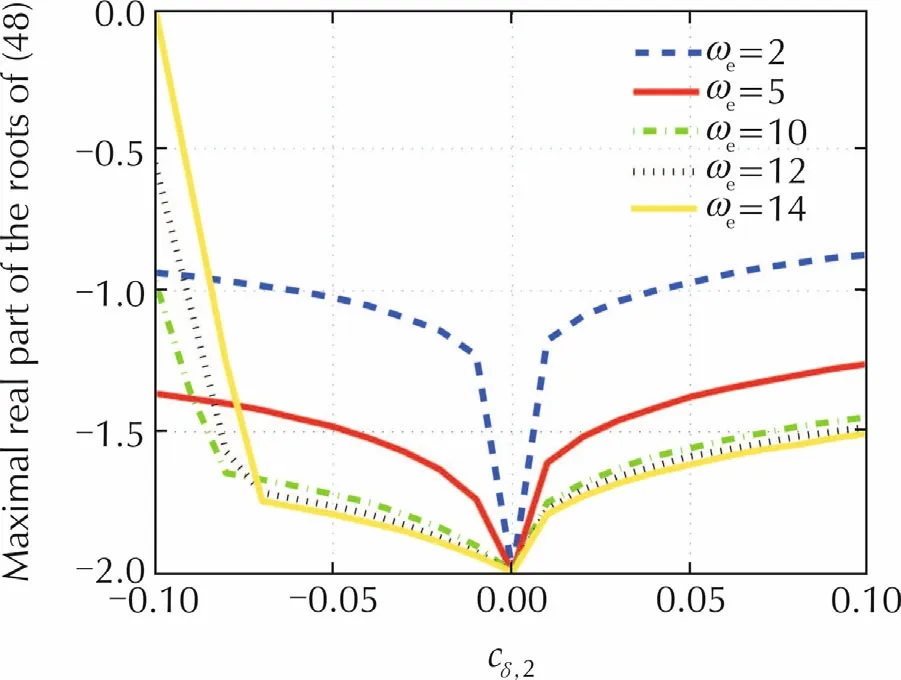
Fig.4 The maximal real part of the roots of(48)for different ωe.

Fig.5 (a)The responses of the corresponding closed-loop system(41),(45)and(47).(b)The estimation of the total disturbance.

Remark 4By the discussion on Examples 1 and 2,the tuning method of ωefor the non-minimum phase system can be presented as follows:obtaining the maximal ωeby the stability of the roots of(19);increasing ωefrom a small value to its maximal value until the actual response meets practical requirements.

6 Conclusions

It is shown that the canonical form selection is crucial for ADRC based control systems,especially for nonminimal phase systems.The paper presents the canonical form for a class of uncertain systems which could have uncertain unstable “zeros”.Also,the necessary and sufficient condition for the stability of the closed-loop system with the proposed canonical form and ADRC is proven under some uncertainties.In particular,we demonstrate that the detectability of the extended system and certain information of the system’s “zeros”are necessary.Additionally,the methods of checking these necessary conditions are discussed via simulation study.We believe that the theoretical results of this paper can provide some fundamental guidelines for designing the canonical form as well as the corresponding ADRC for non-minimal phase systems.

[1]Z.Gao.On the centrality of disturbance rejection in automatic control.ISA Transactions,2014,53(4):850–857.

[2]M.Hou,P.C.Muller.Design of observers for linear systems with unknown inputs.IEEE Transactions on Automatic Control,1993,37(6):871–874.

[3]D.Soffker,T.J.Yu,P.C.Mullter.State estimation of dynamical systems with nonlinearities by using proportionalintegral observer.International Journal of Systems Science,1995,26(9):1571–1582.

[4]M.Nakao,K.Ohnishi,K.Miyachi.A robust decentralized joint control based on interference estimation.IEEE International Conference on Robotics and Automation,Raleigh:IEEE,1987:326–331.

[5]H.Shim,N.H.Jo.An almostnecessary and sufficientcondition for robuststability ofclosed-loop systems with disturbance observer.Automatica,2009,45(1):296–299.

[6]W.-H.Chen,D.J.Ballance,P.J.Gawthrop,et al.A nonlinear disturbance observer for robotic manipulators.IEEE Transactions on Industrial Electronics,2000,47(4):932–938.

[7]L.Guo,S.Cao.Anti-disturbance control theory for systems with multiple disturbances:A survey.ISA Transactions,2014,53(4):846–849.

[8]J.Han.The “extended state observer”of a class of uncertain systems.Journal of Control and Decision,1995,10(1):85–88(in Chinese).

[9] J.Han.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900–906.

[10]C.D.Johnson.Real-time disturbance-observers;origin and evolution of the idea–Part 1:The early years.Proceedings of the 40th Southeastern Symposium on System Theory,New Orleans:IEEE,2008:88–91.

[11]S.Li,J.Yang,W.-H.Chen,et al.Disturbance Observer-based Control:MethodsandApplicaitons.Boca Raton:CRCPress,2013.

[12]A.Radke,Z.Gao.A survey of state and disturbance observers for practitioners.Proceedings of the American Control Conference,Minnesota:IEEE,2006:5183–5188.

[13]Z.Gao.Scaling and bandwidth-parameterization based controller tuning.ProceedingsoftheAmericanControlConference,Colorado:IEEE,2003:4989–4996.

[14]Q.Zheng,Z.Gao.On practical applications of active disturbance rejection control.Proceedings of the 29th Chinese Control Conference,Beijing:IEEE,2010:6095–6100.

[15]R.Schoenberger.Linestream technologies signs licensing deal with Texas instruments.2011:blog.cleveland.com/business_impact/print.html?entry=/2011/07/linestream_technologies_signs.html.

[16]G.Cheng,J.Hu.An observer-based mode switching control scheme for improved position regulation in servomotors.IEEE Transactions on Control Systems Technology,2014,22(5):1883–1891.

[17]H.Liu,S.Li.Speed control for PMSM servo system using predictive functional control and extended state observer.IEEE Transactions on Industrial Electronics,2012,59(2):1171–1183.

[18]J.Linares-Flores,C.Garcia-Rodriguez,H.Sira-Ramirez,et al.Robust backstepping tracking controller for low-speed pmsm positioning system:Design,analysis,and implementation.IEEE Transactions on Industrial Informatics,2015,11(5):1130–1141.

[19]Y.Xia,Z.Zhu,M.Fu,et al.Attitude tracking of rigid spacecraft with bounded disturbances.IEEE Transactions on Industrial Electronics,2011,58(2):647–659.

[20]T.Jiang,C.Huang,L.Guo.Controlofuncertain nonlinearsystems based on observers and estimators.Automatica,2015,59:35–47.

[21]G.Sun,X.Ren,D.Li.Neural active disturbance rejection output control of multimotor servomechanism.IEEE Transactions on Control Systems Technology,2015,23(2):746–753.

[22]Q.Li,D.Li,W.Tan.Performance robustness comparison ofADRC and GPC.Proceedings of the Chinese Control Conference,Hefei,China:IEEE,2012:4586–4590.

[23]H.Xie,K.Song,L.Li,et al.A comprehensive decoupling control method for gasoline hcci combustion.Proceedings of the Chinese Control Conference,Xi’an:IEEE,2013:7681 – 7691.

[24]L.Sun,D.Li,Z.Gao,et al.Combined feedforward and model-assisted active disturbance rejection control for non-minimum phase system.ISA Transactions,2016:DOI 10.1016/j.isatra.2016.04.020.

[25]Y.Huang,W.Xue.Active disturbance rejection control:Methodology and theoretical analysis.ISA Transaction,2014,53:963–976.

[26]Q.Zheng,Z.Chen,Z.Gao.A practical approach to disturbance decoupling control.Control Engineering Practice,2009,17(9):1016–1025.

[27]B.Guo,Z.Zhao.On convergence of the nonlinear active disturbance rejection control for MIMO systems.SIAM Journal of Control and Optimization,2013,51(2):1727–1757.

[28]W.Xue,Y.Huang.Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems.ISA Transaction,2015,58:133–54.

[29]S.Zhao,L.Sun,D.Li,et al.Tracking and disturbance rejection in non-minimum phase systems.ProceedingsoftheChineseControl Conference,Nanjing:IEEE,2014:3834–2839.

[30]C.-T.Chen.Linear System Theory and Design.3rd ed.New York:Oxford University Press,1999.

[31]D.Yoo,S.S.-T.Yau,Z.Gao.Optimal fast tracking observer bandwidth of the linear extended state observer.International Journal of Control,2007,80(1):102–111.