Sampled-data extended state observer for uncertain nonlinear systems

Chuan TIAN ,Peng YAN ,2†,Zhen ZHANG

1.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China;

2.Key Laboratory of High-efficiency and Clean Mechanical Manufacturing,Ministry of Education,School of Mechanical Engineering,Shandong University,Jinan Shandong 250061,China

3.Department of Mechanical Engineering,Tsinghua University,Beijing 100084,China

1 Introduction

The existence of various disturbances and model uncertainties poses major challenges in the design of control systems,where the situation is further complicated in sophisticated control applications with demanding performance requirements such as aerospace industries and modern precision industries.There are abundantresearch results addressing challenging problems on antidisturbance control of systems with parametric variations,unmodeled dynamics and external disturbances.The readers can be referred to[1]and references therein for recent advances in control techniques for disturbance/uncertainty estimation and attenuation.

One major category in anti-disturbance control is disturbance observer based control(DOBC)approach,where disturbance observers are introduced to estimate and compensate the uncertainties and disturbances.Based on the observation mechanism,disturbance observers in both frequency domain[2,3]and time domain[4,5]are proposed in the literature.Alternatively,the method of active disturbance rejection control(ADRC)([6,7])is also well discussed,where successful industry applications have been achieved such as MEMS gyroscopes[8],robotics[9]and high precision motion control[10].As a key part of the ADRC control structure,the extended state observer(ESO)is developed to estimate uncertainties and disturbances simultaneously by lumping them into an an extended state as the“total disturbance”for disturbance elimination purposes.

In recent years,theoretical analysis on the linear ESO(LESO)and the nonlinear ESO(NLESO)has attracted more and more research efforts as well.In[8]and[11],the convergence of LESO is given analytically.Based on time-varying PD-eigenvalues assignmentand Kalman filter algorithms respectively,adaptive extended state observers(AESO)in the form of LESO are presented to improve the performance of ESO and cancel the peaking phenomenon[12,13].To have more design flexibility for complicated systems,[12],nonlinear extended state observer(NLESO)design and analysis are also discussed for both single-input-single-output(SISO)systems[14],and multiple-input-multiple-output(MIMO)cases[15],as well as uncertain lower triangular nonlinear systems[16].Furthermore,the NLESO method is improved by replacing constant observer gains with time-varying gains in[17].

Although most of the results stated above,especially for NLESO,are based on continuous time,the ESO typically needs to be implemented in discrete-time in various computer-based controlapplications.The digitalimplementations of ESO have also received considerable attention,e.g.,different discrete approximation methods[18],the relationship between sampling periods and control bandwidth for LESO[19]and incremental algorithm design[20].In a similar fashion,the discrete form of NLESO is discussed in[7].Note that most of the existing works stated above are designed based on a direct discretization of the plant models.However,many complications in sampled-data systems can not be fully addressed by the design methods discussed above,e.g.,the existence ofperturbationsofsampling schedule[21],or control systems with multiple sampling rates[22].

It is noticed that a continuous-discrete observer method was discussed in[21],where an inter-sample output predictor was used to predict the inter-sample dynamics in sampled-data nonlinear observer design.This design has a hybrid structure because the states are estimated in continuous time and the predictor is updated discontinuously only at the sampling time to correct the estimated state trajectory.Such sampleddata observer design has been widely investigated recently,e.g.,sampled-data high gain observers for networked control systems[23]where sampling periods are nonuniform,and sampled-data extended high gain observers with multi-rate control applications in electrohydraulic actuator systems[22].

Inspired by this line of research on continuousdiscrete observer design,we propose a sampled-data extended state observerdesign with nonlineargain function,where the convergence of the proposed observer is analyzed by a Lyapunov function based method.Meanwhile,the relationship between the observer error bound and the observer gain parameters is also derived.The present work is an extension of[14],which is capable of generating continuous state estimation based on sampled-data system measurement.For applications requiring multiple sampling rates,the proposed design offers the opportunity to compensating high frequency disturbances using an up-sampling compensator,while using the original sampling rate for the rest of control system.For example,when the proposed ESO is employed in an multi-rate ADRC controlframework as illustrated in Fig.1,the inter-sample information(by prediction)can be used to handle high frequency disturbances by up-sampling the observer output,while the feedback controller is still running in the original sampling rate to handle low frequency disturbances.Multi-rate control systems have been successfully implemented in various industry applications such as Hard Disk Drive servo systems[24].

The rest of the paper is organized as follows:In Section 2,some definitions and notations which will be used in this paper are given.The system and continuous time ESO formulation are described in Section 3.The sampled-data nonlinearextended state observerfornonlinear uncertain systems with sampled measurements is proposed in Section 4,where the exponential convergence of the observer is also given by using Lyapunov approach.In Section 5,simulation results are presented to show the effectiveness of the design,followed by conclusions in Section 6.

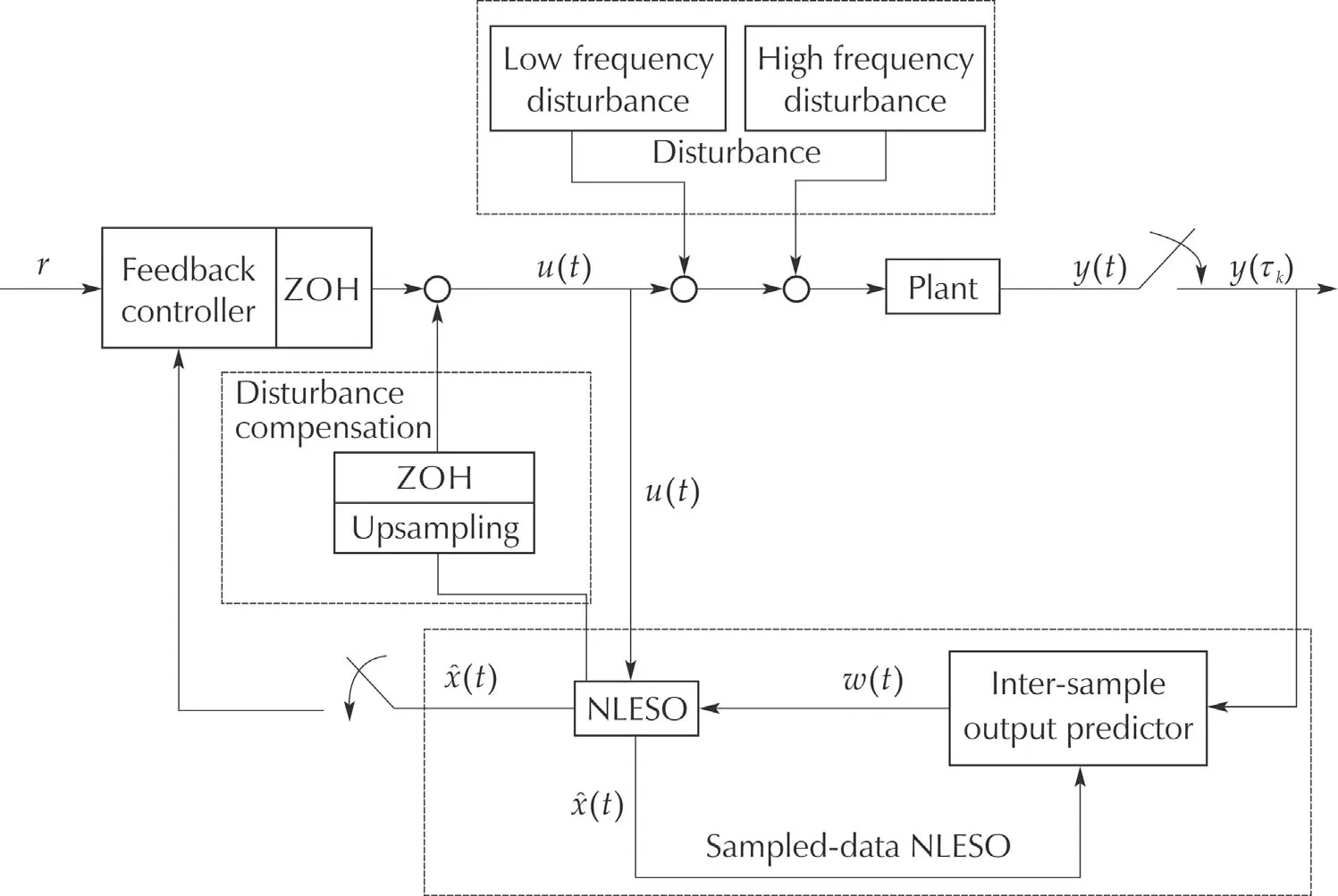
Fig.1 The diagram of sampled-data control system with NLESO.

2 Notations and de finitions

In this section,some mathematical notations used in this paper are introduced.R=(-∞,+∞)is the set of real numbers and Rndenotes the set of real vectors of n-dimension.Cis the continuous function.?·?presents the euclidian norm on Rn.Some countable set

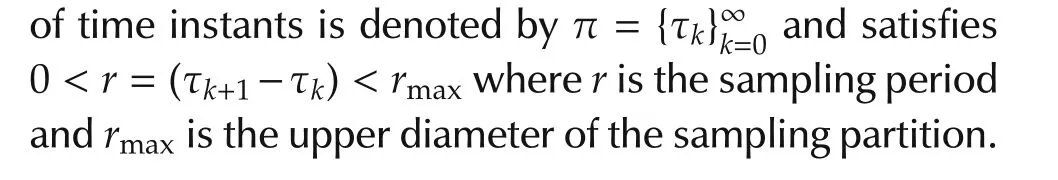
3 Problem formulation

Consider ann-dimensional SISO nonlinear system

wherey∈R is the system output,f∈C(Rn,R)represents a possibly unknown nonlinear dynamics of the system,u∈C(R,R)is the input,bis a given constant,andd∈C(R,R)is the external disturbance.Then system(1)can be presented in the following form:

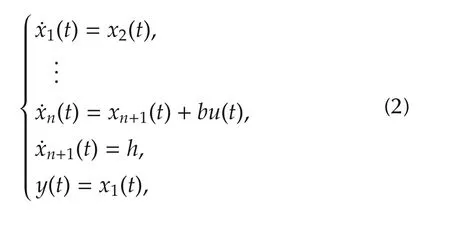
wheref+d,the total disturbance,is set as an extended state of the system,and leth=f˙+d˙,x=[x1x2···xn]T∈ Rnis the state of the system,whose initial values can be set asxi(t0)fori=1,2,...,n.Inspired by the work of[14],a nonlinear extended state observer can be designed for system(2),

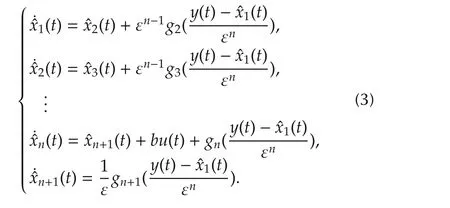
The above observer is a special form of ESO proposed in[6],wherex=[x1···xn+1]∈Rn+1is the estimated state of ESO,the initial condition can be set asxi(t0),the gain ε describes a small positive constant,gi,i=1,2,...,n+1 denote chosen nonlinear functions.According to[14],the error dynamics of the ESO are expected to exponentially converge to 0,namelyx-x→0,as ε → 0 andt→ ∞.

Although the above plant system,as well as the ESO design,can be discretized directly for computerbased digital implementations,some complications(e.g.,nonuniform sampling systems,or multi-rate sam-pling systems)cannot be well addressed.Recall the multi-rate ADRC control architecture depicted in Fig.1,we would like to investigate the sampled-date NLESO design based on discrete time system output and generate continuous observer output,such that the ESO output can be up-sampled to handle high frequency disturbances out of the control bandwidth using original sample rate.For such purposes,we would like to investigate the sampled-data case of NLESO(3)by applying the continuous-discrete observer design technique similar to[21].

Fig.2 The diagram of sampled-data system with NLESO.

4 Sampled-data NLESO design

In this section,we consider the sampled-data NLESO design problem.As depicted in the block diagram in Fig.1,the sampled-data NLESO is composed of an intersample output predictor and a NLESO,where the measurement of the system output is only available at each sampling time.Besides the control inputu,the prediction of outputwis the other input of the NLESO instead of the real system outputy,and some information of state estimations is used in the inter-sample output predictor.The observer is designed in continuous time and the states of the observer can be potentially sampled digitally,even with a sampling time different from that of the output measurement when discretization,thus facilitates multi-rate control system design.

First,we consider system(1)with the sampled-data output measurement as

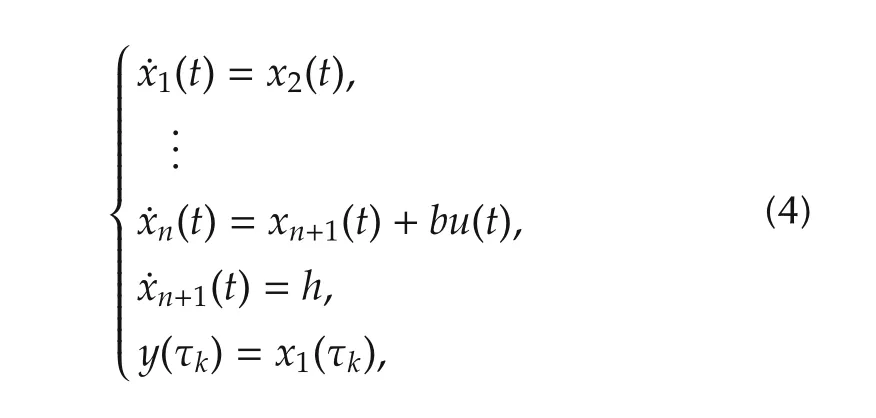
where the output data can be measured at each sampling time τk.Then a sampled-data NLESO with output predictor can be designed as

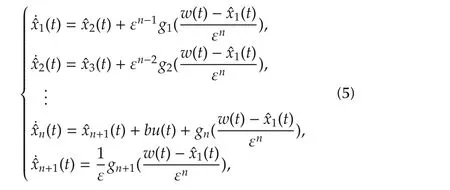
wherexdenotes contious-time estimate state ofx.w(t)is the prediction of outputybetween two consecutive sampling instants,which is updated at the start of each sampling interval.Moreover,the outputpredictorforthe time interval between two consecutive measurements can be shown as

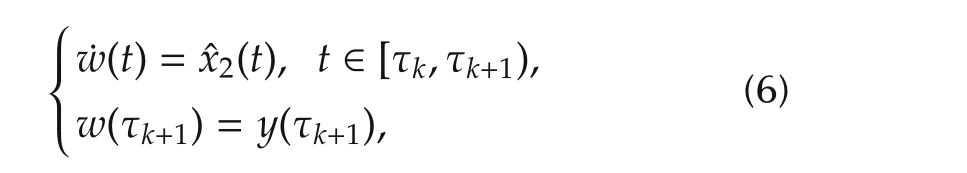
Then,according to systems(4)and(5)we set

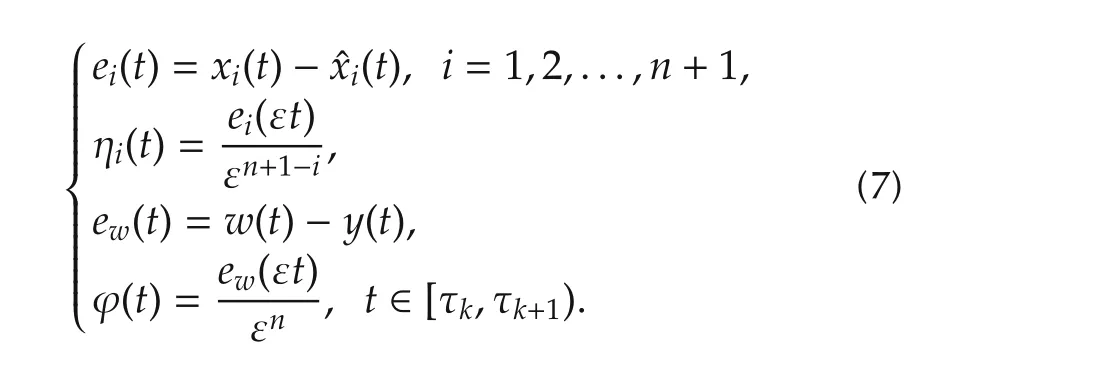
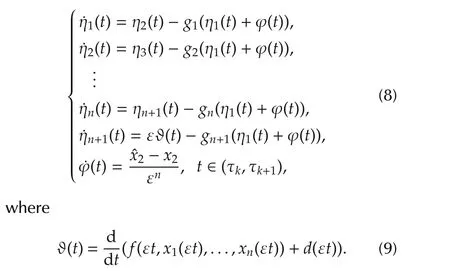
In what follows,we will give the main results of this paper.First of all,some assumptions are made for the sampled-data NLESO.

Assumption 1The unknown functionsf,dare continuously differentiable with respect to their variables,for some positive constantscj,j=0,1,...,nand posi-tive integerq,such that

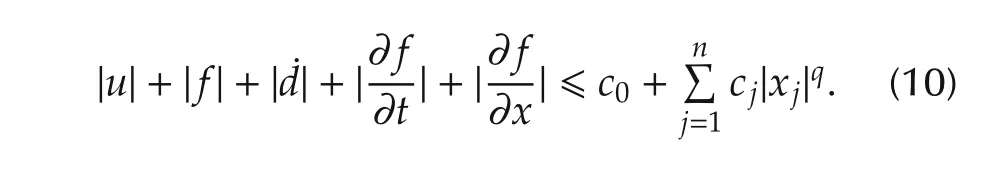
Assumption 2The solutionsxito system(2)and disturbancedsatisfy|d|+|xi(t)|?m1for some constantm1＞0;i=1,2,...,nandt?0.

Assumption 3For∀η =[η1η2···ηn+1]T∈ Rn+1,there exist constants λi,fori=1,...,4 and positive definite radially unbounded and continuous differentiable functionsV1,W1:Rn+1→R such that

Assumption 4Functionsgi(·)∈C(R,R)are globally Lipschitz on a compact set ζ ofz,namely for(z1,z2)∈R×R,there exists γ ＞ 0 such that

Theorem 1Consider the sampled-data system(4).If Assumptions 1–4 hold,then the states of the sampleddata NLESO(5)exponentially converge to the states and extended state of system(4),namely for σ＞0,there exists a sufficiently small ε,a ε-dependentTand a positive boundedrmaxsuch that

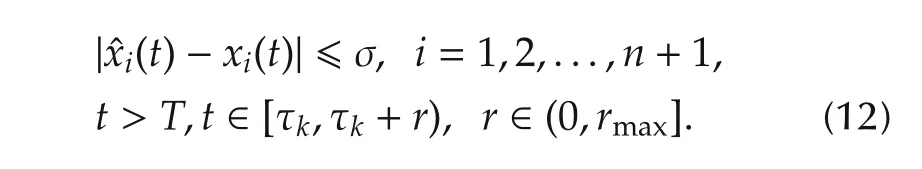
ProofUnder Assumptions 1 and 2 and the dynamic of extended state(9),there exists a constantM＞0,such that|ϑ(t)|?M.

Inspired by[23],we consider the following candidate Lyapunov function:

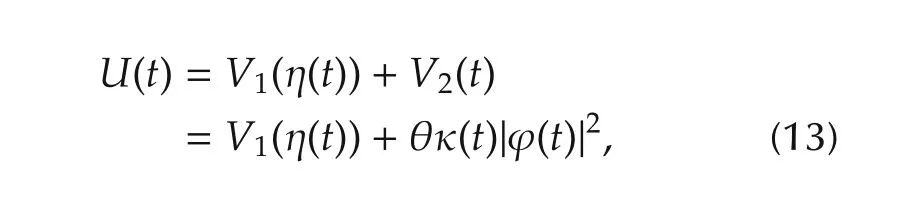
where we introduce an additional termV2(t)with respect to the output predictor,θ is a positive constant which can be computed as follows and κ(t)is a positive and bounded function.This function satisfies the following conditions:

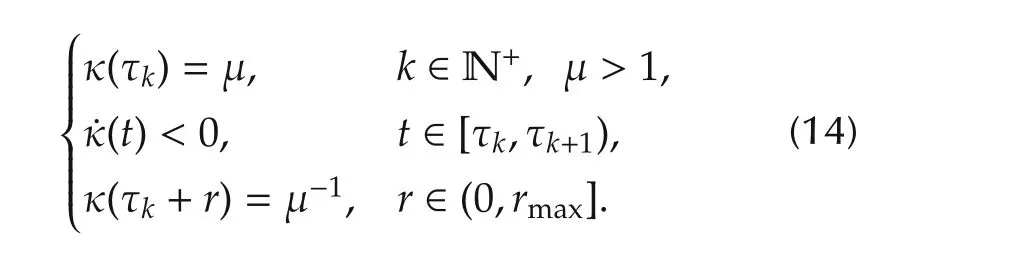
First,under Assumptions 3 and 4,we consider the time derivative ofV1(η(t))along the solution η(t)to system(4),and obtain

The following bound regarded to(15)can be derived by recalling the Young inequality:

Combining(17)with(18),we can obtain

By Assumption 3 again,integrating(24)on the interval[τk,t]yields

Consider(12)–(14)and the fact that ϕ(τk)=0,η(τk)=η(τ-k)at the time instantt= τk,then we will have

It means that the observer error is ultimately bounded and we can choose ε small enough to reduce the bound of error.Moreover,the right hand side of(30)converges exponentially to 0,as ε→ 0.In addition,we can compute the value ofrmaxas

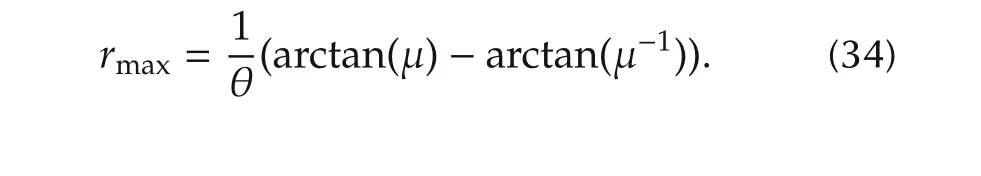
5 Numerical simulations

In this section,a numerical example is given to illustrate the effectiveness of the proposed observer.Inspired by[14]and[17],consider the following nonlinear

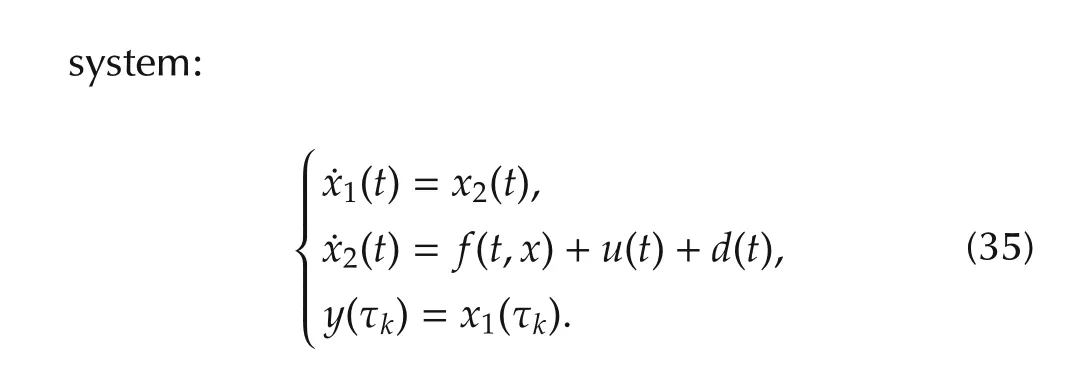
We take the system inputu(t),external disturbanced(t),and nonlinear functionf(t,x)in the above system respectively as

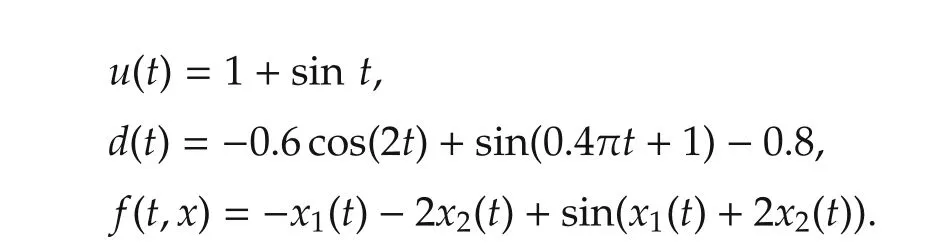
By following the design procedure in the above section,We can design the following sampled-data nonlinear extended state observer

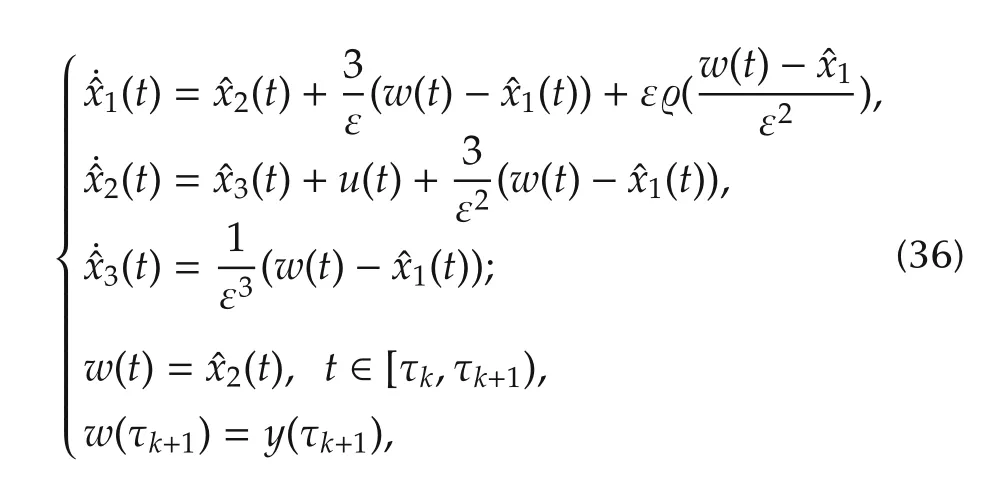
where the nonlinear function ϱ :R → R is defined as

In this case,the global Lipschitz nonlinear functionsgiin the ESO in(5)can be specified as

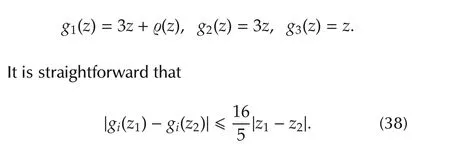
Note that Assumptions 1–4 are all satisfied.Thus,(36)is a well-defined sampled-data NLESO for system(35)according to Theorem 1.Now we can define the Lyapunov function as

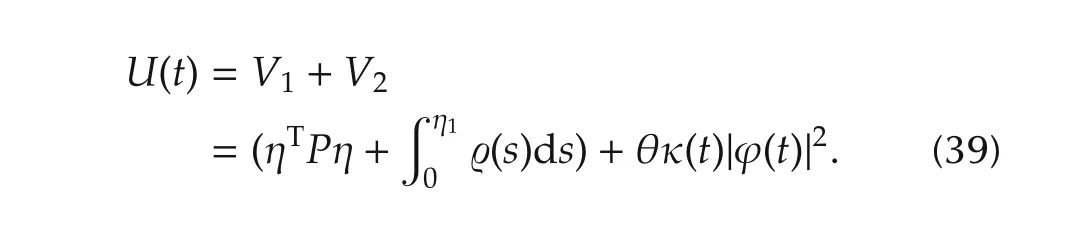
The positive definite matrixPcan be chosen according to[14],and the convergence can be guaranteed by the method presented in Section 4.

The initial states of the plant(30)and the ESO(31)are set as(1,1)Tand(0,0,0)T,respectively.The time step for calculation is 0.005 s,and the sampling time of the output measurement isr=0.01 s.

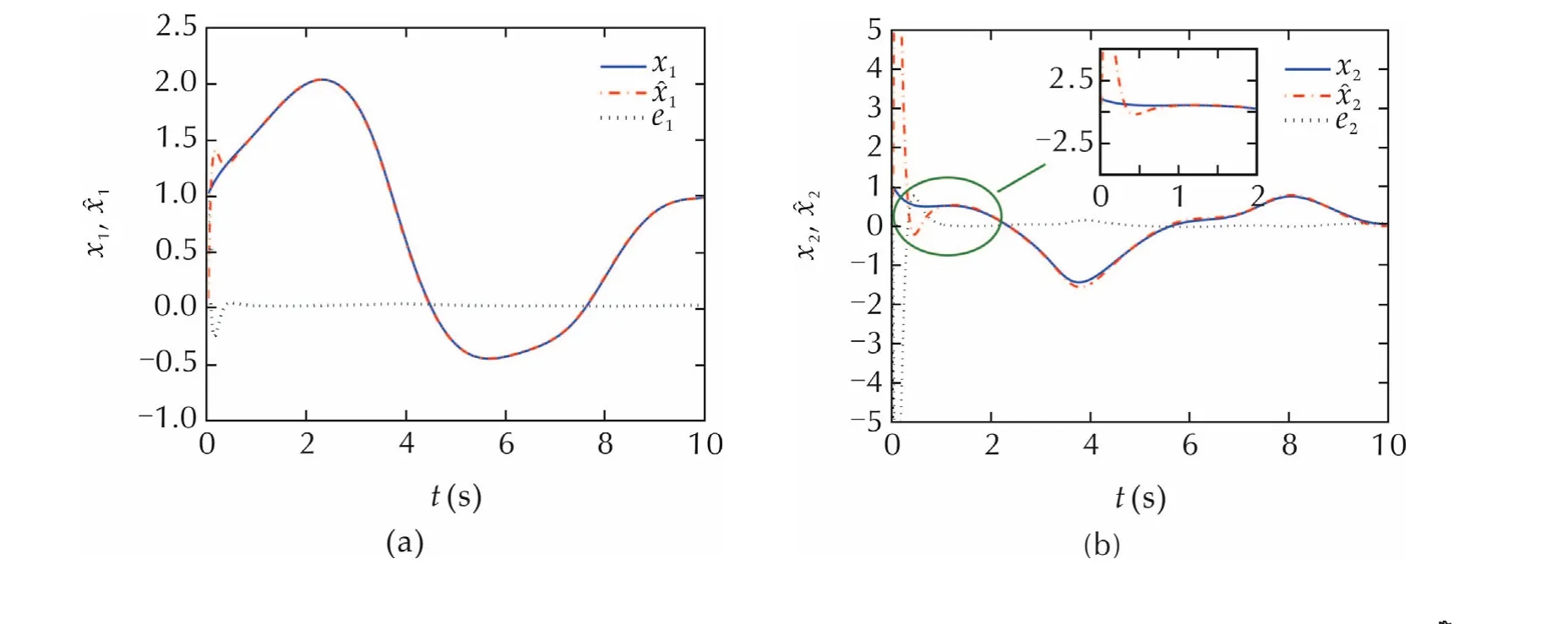
Fig.3 Numerical simulations for system(32)by sampled-data NLESO y and w.

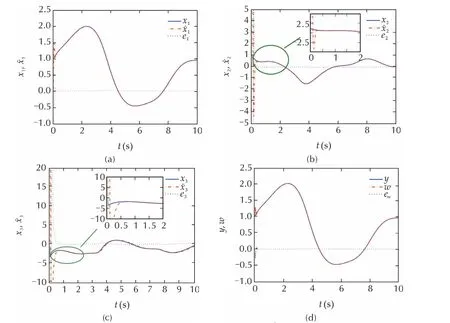
Fig.4 Numerical simulations for system(32)by sampled-data y and w.

6 Conclusions

In this paper,a sampled-data nonlinear extended state observer for uncertain nonlinear systems subject to discrete time measurement was developed,where the inter-sample dynamics and sampling schedule were considered.The exponential convergence of the observer was analyzed by introducing a Lyapunov function chosen for hybrid systems.The relations between the observer error bound and the observer parameters were explicitly given.The numerical simulation results demonstrated the convergence ofthe proposed observer and inter-sample output predictor.Future works,along this line of research,include sampled-data ADRC or sampled-data output feedback control based on the proposed observer,as well as their industrial applications.

[1]W.-H.Chen,J.Yang,L.Guo,et al.Disturbance observer-based control and related methods:An overview.IEEE Transactions on Industrial Electronics,2015,63(2):1083–1095.

[2]K.Ohishi,M.Nakao,K.Ohnishi,et al.Microprocessor controlled DC motor for load-insensitive position servo system.IEEE Transactions on Industrial Electronics,1987,34(1):44–49.

[3]E.Sariyildiz,K.Ohnishi.Stability and robustness of disturbanceobserver-based motion control systems.IEEE Transactions on Industrial Electronics,2015,62(1):414–422.

[4]L.Guo,W.-H.Chen.Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach.International Journal of Robust and Nonlinear Control,2005,15(3):109–125.

[5]J.Yang,S.Li,X.Yu.Sliding-mode control for systems with mismatched uncertainties via a disturbance observer.IEEE Transactions on Industrial Electronics,2013,60(1):160–169.

[6]J.Han.A class of extended state observers for uncertain systems.Control and Decision,1995,10(1):85–88(in Chinese).

[7]J.Han.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900–906.

[8]Q.Zheng,L.Dong,D.H.Lee,et al.Active disturbance rejection control for MEMS gyroscopes.IEEE Transactions on Control Systems Technology,2009,17(6):1432–1438.

[9]S.E.Talole,J.P.Kolhe,S.B.Phadke.Extended-stateobserver-based control of flexible-joint system with experimental validation.IEEE Transactions on Industrial Electronics,2010,57(4):1411–1419.

[10]T.Leng,P.Liu,P.Yan,et al.Modeling and active disturbance rejection control for a piezoelectric-actuator driven nanopositioner.Proceedingsofthe33rdChineseControl Conference,Nanjing:IEEE,2014:5910–5915.

[11]Q.Zheng,L.Dong,Z.Gao.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknow dynamics.Proceedings of the IEEE Conference on Decision and Control,New Orleans:IEEE,2007:3501–3506.

[12]Z.Pu,R.Yuan,J.Yi,et al.A class of adaptive extended state observers for nonlinear disturbed systems.IEEE Transactions on Industrial Electronics,2015,62(9):5858–5869.

[13]W.Xue,W.Bai,S.Yang,et al.ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines.IEEE Transactions on Industrial Electronics,2015,62(9):5847–5857.

[14]B.Guo,Z.Zhao.On the convergence of an extended state observer for nonlinear systems with uncertainty.Systems&Control Letters,2011,60(6):420–430.

[15]B.Guo,Z.Zhao.On convergence of non-linear extended state observer for multi-input multi-output systems with uncertainty.IET Control Theory&Applications,2012,6(15):2357–2386.

[16]B.Guo,Z.Zhao.Extended state observer for uncertain lower triangular nonlinear systems.Systems&Control Letters,2015,85:100–108.

[17]B.Guo,Z.Zhao.On active disturbance rejection control for nonlinear systems using time-varying gain.European Journal of Control,2015,23:62–70.

[18]R.Miklosovic,A.Radke,Z.Gao.Discrete implementation and generalization of the extended state observer.Proceedings of the American control conference,Minneapolis:IEEE,2006:2209–2214.

[19]S.Shi,J.Li,S.Zhao.On design analysis oflinearactive disturbance rejection control for uncertain system.International Journal of Control and Automation,2014,7(3):225–236.

[20]G.Herbst.Practical active disturbance rejection control:Bumpless transfer,rate limitation and incrementalalgorithm.IEEE Transactions on Industrial Electronics,2016,63(3):1754–1762.

[21]I.Karafyllis,C.Kravaris.From continuous-time design to sampled-data design ofobservers.IEEETransactionsonAutomatic Control,2009,54(9):2169–2174.

[22]A.A.Sofiane.Sampled data observer based inter-sample output predictor for electro-hydraulic actuators.ISA transactions,2015,58:421–433.

[23]T.Ahmed-Ali,F.Lamnabhi-Lagarrigue.High gain observer design for some networked control systems.IEEE Transactions on Automatic Control,2012,57(4):995–1000.

[24]H.Fujimoto,Y.Hori.High-performance servo systems based on multirate sampling control.Control Engineering Practice,2002,10(7):773–781.