基于曲线拟合法太阳影子定位技术的研究

黄玲，杨鹏辉*，谢文，吴春艳

(安徽财经大学a.统计与应用数学学院；b.金融学院，安徽蚌埠　233030)



基于曲线拟合法太阳影子定位技术的研究

黄玲a，杨鹏辉a*，谢文a，吴春艳b

(安徽财经大学a.统计与应用数学学院；b.金融学院，安徽蚌埠233030)

[摘要]本文主要研究太阳影子定位技术，以太阳高度角为切入点，借助天文三角形知识，探究太阳高度角、太阳方位角、太阳时角、太阳赤纬与经纬度、日期、地方时的关系，结合曲线拟合、联立方程式的方法，建立太阳影子定位的优化模型，运用MATLAB、EXCEL软件研究出太阳影子的变化规律、基于影子顶点坐标条件下物体的定时、定位，并将研究结果推广到视频数据分析领域对视频进行定位、定时.

[关键词]太阳影子定位；太阳高度角；曲线拟合；视频数据分析；MATLAB

0引言

太阳影子定位技术就是通过水平地面上物体太阳影子的长短变化，确定物体所在的地点.影长与太阳高度角以及物体高度之间存在函数关系，太阳高度角[1]作为研究切入点，将影响太阳影子的因素主要细分为物体所在地的经纬度以及影长所对应的日期与时刻.本文旨在探究物体影长与其影响参数之间的关系，建立太阳影子定位模型，并将此模型应用到视频数据分析领域，根据视频中某一物体的太阳影子变化，确定拍摄的地点与拍摄日期.

1数据的获取与假设

本文中物体太阳影子的顶点坐标数据以及视频数据均来自2015年全国大学生数学建模题A题[2].为了方便求解，提出以下五条假设：11假设采集影子顶点数据时，天气晴朗，无恶劣天气出现；22假设大气对太阳光线的折射很小，太阳光线到达地球后依旧是平行的；33假设地球公转的速度即太阳直射点在南北回归线之间的移动是匀速的；44假设附件所提供的数据均是真实测量的，不含人为修改的因素；55假设摄像机参数、摄像机的几何畸变在提取视频中影子顶点坐标时产生的误差可忽略不计.

2影子长度关于经纬度、日期、时刻的变化规律

2.1研究思路

影子长度等于直杆长度与太阳高度角正弦值的比值，影子长度、直杆高度、太阳高度角分别用L、H、h表示，太阳高度角作为本文研究的切入点，在天文三角形[3]中其大小由当地纬度α、当日的太阳赤纬[1]φ以及当时的太阳时角[1]ω决定，

sinh=sinαsinφ+cosαcosφcosω[3]

(1)

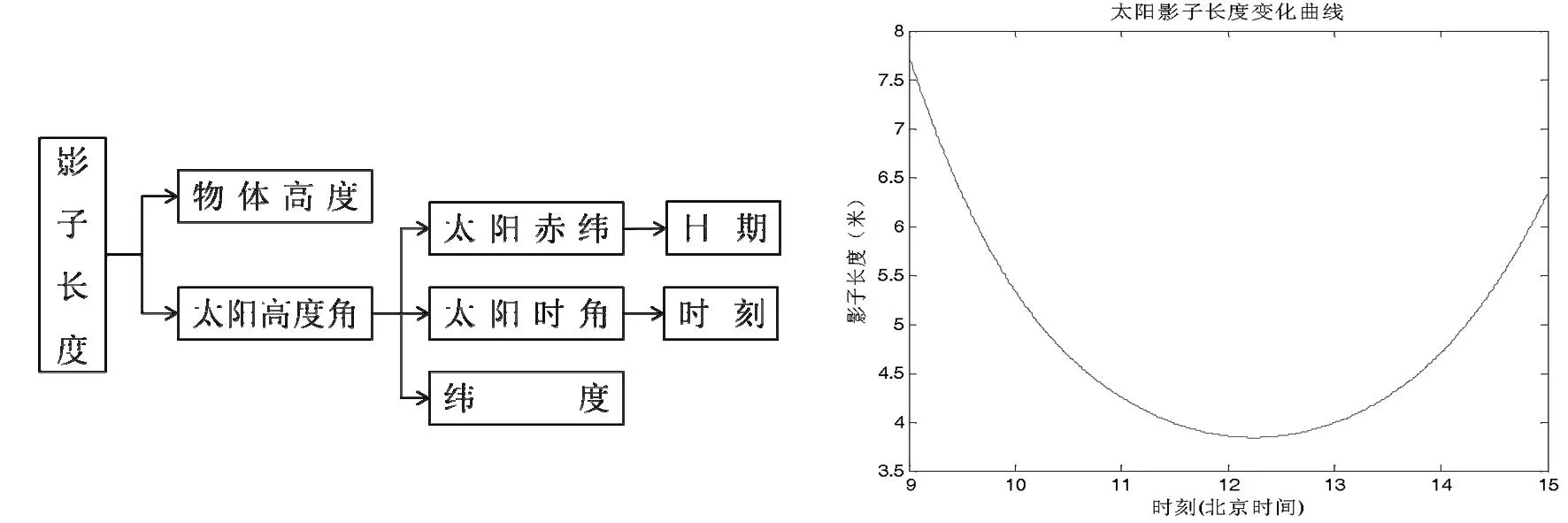
图1　影长变化规律的研究思路图　　图2　天安门3米高直杆的太阳影子变化图

2.2研究方法

本文通过影子长度关于各影响参数之间的函数关系，联立方程组，建立影子长度变化模型，进而对其研究规律进行探究；其中有关太阳时角大小的地方时t的计算，首先要选取一地为标准时间，本文以北京时间T(东经120°)为例,再根据计算得出的该地经度与东经120°的经度差，得出地方时的计算模型，如下：

(2)

根据地方时的计算公式，将太阳时角的算法进行改进：

(3)

其中地方时t在计算时需注意，当t<0时，地方时t加24，日期减一天；当t>24时，地方时t减24，日期加一天.

联合影子长度、太阳高度角、太阳赤纬以及改进的太阳时角的计算公式，影子长度变化模型可表示如下：

(4)

2.3数据分析

利用MATLAB对模型进行编程，以2015年10月22(d=295)日北京时间9：00(T=9)-15：00(T=15)之间天安门广场(北纬39度54分26秒,东经116度23分29秒)3米高的直杆为例，带入模型研究其太阳影子长度的变化规律，求解出天安门广场直杆影长的结果如表1所示：

表1　天安门直杆影子长度统计表

根据不同时刻影子的长度利用MATLAB软解绘制直杆的太阳影子关于时间变化的图，并结合Spline插值法绘制直杆的太阳影子关于时间变化的光滑曲线图，结果如图2所示：

由上述分析可知，固定杆太阳影子长度的总体变化趋势呈U型，从日出时刻开始到当地地方时为正午12点时，影子长度逐渐减小，并在该地正午十二点时达到最小值；之后从正午十二点直到日落时刻，影子长度逐渐增大并在日落时刻消失.

3基于日期、影子顶点坐标条件下的太阳影子定位

3.1研究思路

以水平地面为空间xoy平面，物体底端中心为空间坐标系原点建立空间直角坐标系，根据各个时刻下影子的顶点坐标以及数据记录的日期确定物体所处的地点.本文从两个方面来考虑，一方面是对经度进行定位，需要根据物体所在地的地方时与北京时间的时差，利用改进的太阳时角计算公式，确定物体所处地点的经度值，对于时差的计算，我们将影长数据与所对应的北京时间利用最小二乘法进行曲线拟合，推算出影子长度达到最小也就是当地时间为正午十二点时所对应的北京时间；另一方面是对纬度进行定位，我们引进太阳方位角[5]，其计算公式为：

(5)

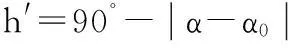
3.2数据处理

利用2015年4月18日某固定直杆在水平地面上的太阳影子顶点坐标数据(见表2)，分别对影子长度与北京时间以及影子顶点的横纵坐标进行曲线拟合.

表22015年4月18日某固定杆太阳影子的顶点坐标数据

1)影长与北京时间的曲线拟合

运用MATLAB软件画出影子长关于北京时间的散点图并利用最小二乘法进行曲线拟合，结果如图3所示.

可得到影长与北京时间之间的拟合函数L= 0.1489T2- 3.7519T+ 24.1275.

1)影子顶点坐标的曲线拟合

对表2中影子的顶点坐标用MATLAB软件画出散点图并这些数据进行曲线拟合，结果如图4所示:

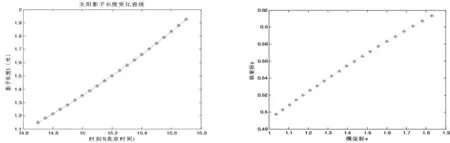
图3　太阳影子长度关于时间变化的拟合曲线　　图4　影子顶点纵坐标关于横坐标的曲线拟合

可得到影子顶点的横、纵坐标之间的拟合函数y=- 0.0258x2+ 0.2206x + 0.2965.

3.3研究方法

已知当某地的直杆的太阳影子长度L达到最小值时，该地地方时为正午十二点，我们根据影长与北京时间拟合的二次函数L= 0.1489T2- 3.7519T+ 24.1275，求出影长的最小值以及该点多对应的北京时间T，再根据北京时间T与地方时t之间的时差，通过地方时计算模型求解得出该地的经度β.

由于太阳方位角满足tanA=y/x公式，结合影子顶点坐标的曲线拟合结果，并通过影子的顶点坐标计算影子长度L2=x2+y2，联立方程组，建立任意影长下的太阳方位角的计算模型：

“公共法律服务智能化建设不仅有效提升服务均等化水平，还具有社会治理的深远意义，技术变迁再次成为影响社会治理变迁的重要因素。⑱黄东东：《公共法律服务与信息技术：域外经验与中国问题——以法律援助为例》，《电子政务》，2017年第1期。”随着不同形态样式智能化产品应用在公共法律服务项目中，公共法律服务智能化成为一个不断发展演进的概念。特别是在共享经济背景下，公共法律服务智能化模式以服务网络平台开发利用为主线，并辅以视频技术、人工智能技术等信息技术支持，构建出新型的公共法律服务体系。

(6)

(7)

我们联合正午时刻的太阳方位角与正午太阳高度角建立纬度定位模型：

(8)

3.4结果分析

根据上述所建模型，利用MATLAB编程进行求解，通过二次函数顶点坐标公式可以求出影子长度最低时对应的北京时间，结果如下：

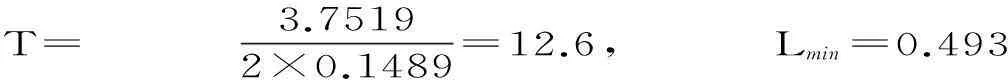
T= 3.75192×0.1489=12.6, Lmin=0.493

(9)

即当时北京时间为12：36，带入经度定位模型

(10)

求解结果得出该地经度为东经111度.

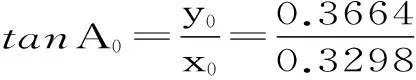
结合经度、纬度求解结果，该直杆所在位置有两个其一是我国海南省(18.49°N,111°E),其二是在印度尼西亚(4.38°N,111°N).

4基于影子顶点坐标条件下的定时、定位

4.1研究思路

根据物体太阳影子的顶点坐标数据，以及该数据所对应的北京时间，对该物体所在地点进行定位，并确定当天的日期，这是在基于日期、影子顶点坐标条件下的太阳影子定位研究上的进一步深入.在上述研究分析中可以看出，经度的确定于日期无关，所以在此问题上，本文只需进一步研究在没有日期这一条件下如何确定纬度值，并分析数据记录的日期.

4.2研究方法

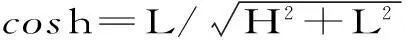
(11)

其中太阳时角又可以表示如下：

(12)

带入上述模型，综合可得：

(13)

4.3数据处理

利用某固定直杆在水平地面上的太阳影子顶点坐标数据(见表3)

表3某固定直杆太阳影子顶点坐标数据

根据所建模型可知表3中每3次记录数据可得出一组解，本文利用MATLAB软件将数据带入模型进行求解，求解结果如表4所示：

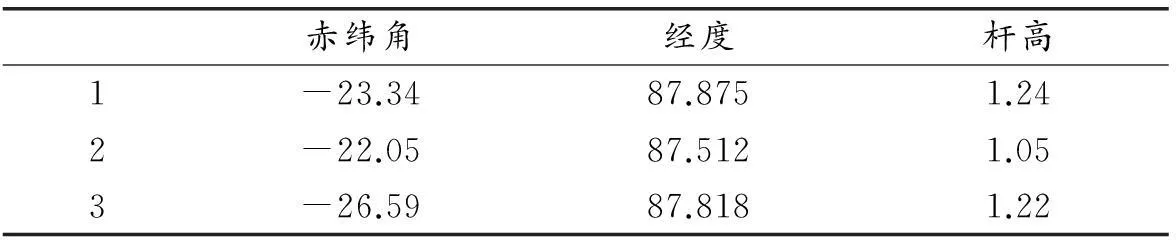
表4　结果统计表

由于三组求解结果相差甚微，本文为减小误差，将三组数据进行平均，利用太阳赤纬与日期的关系：

φ=23.45°sin360°(284+d)/365求解得到d=84，故当天日期应该为3月25日；利用太阳高度角的计算公式sinh=sinαsinφ+cosαcosφcosω求解得到α=43.8°N.

4.4结果分析

综合上述分析结果，该固定直杆所在地点在我国新疆维吾尔自治区的乌鲁木齐市(43.8°N,87.74°E)，当天日期为3月25日.

5太阳影子定位技术在视频数据分析领域的推广

5.1研究思路

如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，通过本文的研究，可以根据视频中物体的太阳影子变化，利用视频图像信息的量化处理技术将图像信息转化为数据，得出视频中太阳影子的顶点坐标数据，并将数据带入上述研究所建模型确定视频的拍摄地点与日期，本文将以2015高教社杯全国大学生数学建模竞赛试题A题的视频附件为例.

5.2研究方法

首先将视频文件导入MATLAB中，每三分钟提取视频一帧，得到20组视频截图，以直杆的底端中心为原点，直杆所在方向为y轴正方向建立直角坐标系，在此基础上提取影子的顶点像素坐标数据；

接着，根据针孔摄像机成像原理，将图片中的图像坐标转化为实际坐标，得出直杆影子顶点变化的实际空间坐标值，数据整理表5所示：

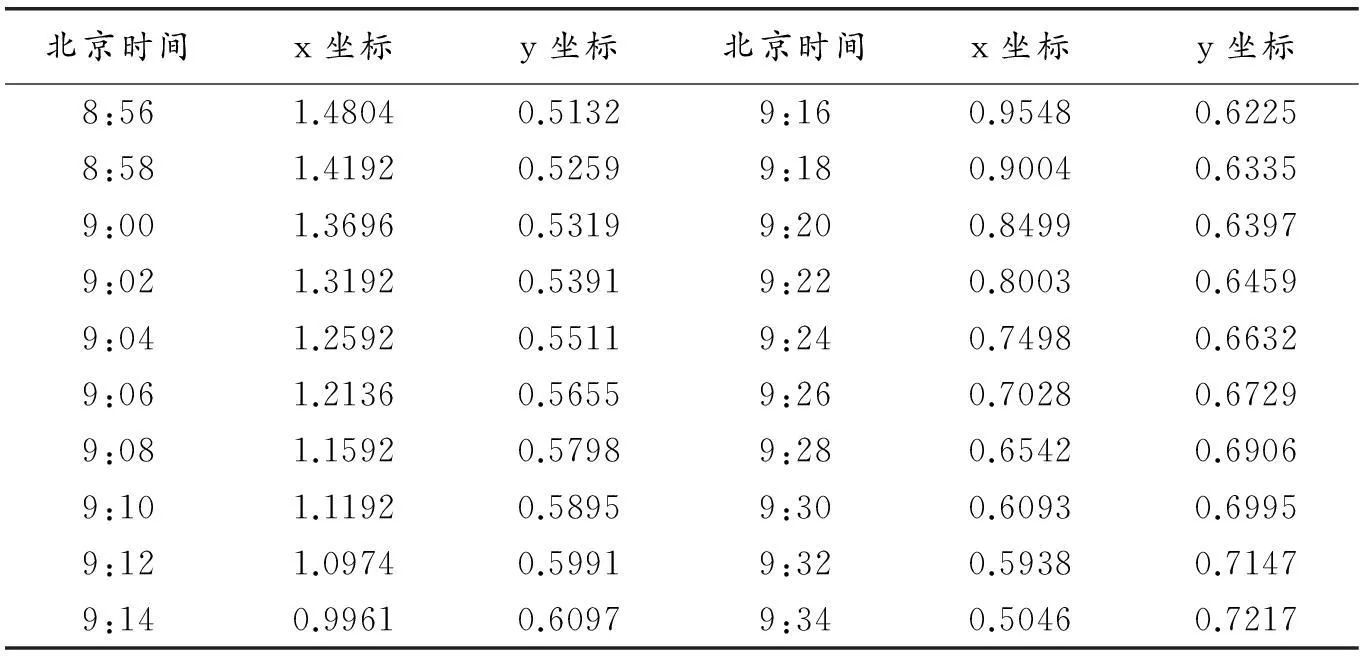
表5　视频中直杆影子顶点坐标

5.3 结果分析

已知视频的拍摄时期为2015年7月13日，将表5中整理的影子点坐标数据利用MATLAB软件带入第二节所建模型进行求解，结果表明拍摄地点可能是在我国黑龙江省境内(47.8°N,133°E)；剔除拍摄日期这一已知条件，将数据带入第三节的模型中进行求解，结果表明拍摄日期为2015年3月31日前后，拍摄地点在我国钓鱼岛附近(37.32°N,133°E).

6总结

本文通过对太阳影子的变化规律、根据太阳影子的顶点坐标数据对物体进行定位、定时的逐步探究，研究出太阳影子定位技术，并结合视频信息的量化处理方法，将此项技术运用到视频数据分析领域，确定视频的拍摄地点与日期.

参考文献

[1]谈小生,葛成辉.太阳角的计算方法及其在遥感中的应用[J].北京:国土资源遥感,1995:48-57.

[2]2015年高教社杯全国大学生数学建模竞赛赛题,http://www.mcm.edu.cn/html_cn/node/ac8b96613522ef62c019d1cd45a125e3.html,访问时间(2015-09-14).

[3]金祖孟.地球概论(第三版)[M].北京:高等教育出版社,1997.

[4]彭海仔.基于T-S模糊模型的太阳位置算法[J].上海海事大学学报,2014,35(2):2-16．

[5]郑鹏飞,林大钧,刘小羊,等.基于影子轨迹线反求采光效果的技术研究[J].华东理工大学学报(自然科学版),2010:458-463.

[责任编辑：房永磊]

The Study of Positioning Technology of the Model of Sun's Shadow Based on the Curve Fitting

HUANG Linga，YANG Peng-huia，XIE Wena，WU Chun-yanb

(Anhui University of Finance and Economics ,a. School of Statistics and Applied Math；b. School of Finance,Bengbu 233030,China)

Abstract:The thesis majors in the positioning of sun's shadow, in our study, solar height angle is breakthrough, by means of the knowledge of the astronomical triangle, we analysed the quantitative relationship between sun elevation angle, solar azimuth, solar hour, solar declination angle and longitude, latitude, date, local time. Combining with the method of curve fitting and simultaneous equations, we set up the sun’s shadow positioning optimizing model. By using MATLAB and EXCEL software, we worked out the laws for the change of sun’s shadow, and ascertained the location and date. Finally we promoted our research result to the field of video data analysis.

Key words:sun’s shadow positioning; sun elevation angle; curve fitting; video data analysis; MATLAB

[中图分类号]O185.1

[文献标识码]A

[文章编号]1004-7077(2016)02-0041-07

[作者简介]杨鹏辉(1981-)，女，安徽淮南人，安徽财经大学统计与应用数学学院讲师，硕士，主要从事图论与组合优化研究.

[基金项目]国家自然科学基金项目(项目编号：11301001).

[收稿日期]2016-01-21