对称性计算分子振动频率的研究

杨慧

(忻州师范学院物理系,山西忻州　034000)



对称性计算分子振动频率的研究

杨慧

(忻州师范学院物理系,山西忻州034000)

[摘要]本文利用分子几何结构的对称性质，用对称性群计算具有对称性分子的振动频率，这种方法是非常适用于计算具有高度对称性分子振动问题的，因为只需考虑分子的局部所受的力场，简化了计算过程.

[关键词]对称群;振动频率;投影算符

0引言

在以往分子振动频率的计算中所采用力常数模型计算，有一项重要任务就是处理含参数的高阶厄米矩阵的本征值问题，对动力学矩阵中的参数进行调整使其与实验上准确测到的振动频率有最佳的拟合，进而计算出分子的振动频率，此方法的最大问题就是计算工作量太大，一般情况下比较难处理[1-2].

Feidman等人采用群论的方法来简化动力学矩阵，降阶后得到的分块矩阵再用非线性最小二乘法进行拟合，由于分块矩阵的阶数较高，所以在拟合中，计算量仍然很大[3-4].对称操作是使具有几何形状的实体自身重合的操作，由对称操作的集合构成的群称作对称性群[5]. 本文利用分子具有高度对称性这一特点，利用对称操作群推导计算具有高度对称性分子振动频率，简化了以往的计算过程.

1对称群对分子振动频率的计算推导

用经典力学来求解问题，在分子振动时原子间存在着一种相互作用，这种相互作用使得原子在平衡位置附近作耦合振动，相当于弹簧质量模型[5].在这种模型下每个键和键角用弹簧代替，原子用质点来代替，n个原子的自由度为3n，其中质心平动有3个自由度，n个原子组成的分子的拉格朗日方程可以写成如下的形式：

L=T-V

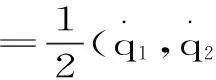
(1)

振动本征频率由下面的行列式获得：

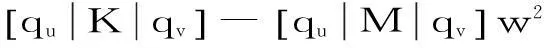
(2)

(u,v=1,2,…3n)

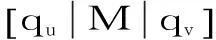
不可约表示α取不同的值，通过解久期方程可以求得相应的振动频率w.

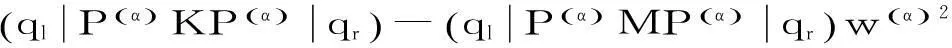
(3)

(4)

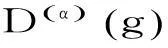
(5)

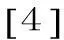
(6)

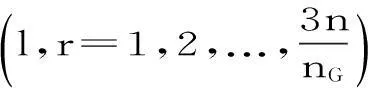
α不可约表示的模表示为：

(7)

(h=a,bforE;h=a,b,cforT;h=a,b,c,dforG,h=a,b,c,d,eforH)

参考文献

[1]Negri F,Orlandi G.Vibrationsl Frequencies of C60[J].Chem Phys lett,1988,144(1):31-33.

[2]MA Hong-Cai ,LoU Sen-Yue.Non-Lie Symmetry Group of (2+1)-Dimensional Nonlinear Resonant Davey-Stewartson System [J].Commun Theor Phys,2011,5(55):737-740.

[3]郭文录,饶倩,张秀荣.PtIr0(n=1～5)团簇电子结构与振动光谱的理论研究[J].计算物理学，2012,6(29):921-923.

[4]Zhang Yun-Guang,Zha Xin- Wei,Calculation of the vibrational frequency and isotopic shift of UF6 and U2F6[J].Chin.Phys.B,2012,7(21) 073301.

[5]徐婉棠,喀兴林.群论及其在固体物理中的应用[M].北京:高等教育出社,1995.

[责任编辑：闫昕]

Research of Molecule' s Vibrational Frequencies by Symmetry

YANG Hui

(Department of Physics , Xinzhou Teachers University,Xinzhou,034000,China)

Abstract:Based on geometrical symmetry of molecular structure, we proposed a computational method for vibrational frequenciesof molecules with high symmetry. The method is powerful to deal with vibrational problems of the molecules of high symmetry,only the force field of a single carbon atom is calculated ,which simplify computational process.

Key words:symmetric group ;vibrational frequencies ;projection operator

[中图分类号]O561.3

[文献标识码]A

[文章编号]1004-7077(2016)02-0008-02

[作者简介]杨慧(1982-)，女 ，山西忻州人，忻州师范学院物理系讲师，理学硕士，主要从事原子与分子物理的研究.

[收稿日期]2016-01-29