基于ARMA模型的南京市PM2.5浓度分析与预测

刘玲，宋马林

(安徽财经大学统计与应用数学学院，安徽蚌埠　233030)



基于ARMA模型的南京市PM2.5浓度分析与预测

刘玲，宋马林*

(安徽财经大学统计与应用数学学院，安徽蚌埠233030)

[摘要]针对PM2.5浓度的时间分布，运用南京市2014年PM2.5日浓度时间序列，利用时间序列分析的Box-Jenkins建模思想，结合EViews7得到符合南京市PM2.5浓度变化的ARMA(5,3)模型，并预测出2015年1月1日至5日的PM2.5浓度，通过与实际数据相对照，发现模型具有较好的拟合性，适用于大气中PM2.5浓度分析与预测.

[关键词]PM2.5；时间序列；EViews7；ARMA模型；预测

0引言

大气为地球上的生命繁衍以及人类发展提供了理想的环境.它的状态和变化，无时无刻影响着人类的生产、生活甚至生存.近年来，随着经济的迅猛发展，大气污染问题也越来越严重.空气质量问题已然是政府、环境保护部门和全国人民关注的热点问题.据中国国家发展和改革委员会2013年7月11日在官方网站上公布的一份报告披露：自2013年初以来，中国发生大范围持续雾霾天气.据统计，我国约1/4的国土面积、6亿人受到雾霾的影响，包括华北平原、黄淮、江淮、江汉、江南、华南北部等地区[1]，其中，PM2.5被认为是造成雾霾天气的“元凶”.

大气中PM2.5的污染已经引起了国内外环境和大气科学家的广泛关注，其中以美国对于PM2.5的研究开展得最早，也最为深入.中国对于PM2.5等颗粒物的研究起步相对较晚，近年来由于空气污染日益严重，国内的研究工作越来越受到重视.前期研究工作主要是分析PM2.5的浓度特征以及成分和来源，杨凌霄(2008)通过对济南市PM2.5的深入研究，阐述了其PM2.5的污染水平和影响因素[2].近年来对于PM2.5浓度与气象条件关系的研究也逐渐增多，刘辉(2011)等通过对实测数据的分析，得出气象条件是除污染源排放外影响PM2.5浓度的重要因素[3].随着目前学术界对PM2.5研究的逐渐深入，国内相关研究也逐步增多，近两年尤以PM2.5的时空分布居多，张振华(2014)对北京市PM2.5的污染水平和时空分布特征进行了研究[4]，卢鹏(2014)等运用高斯扩散模型研究了PM2.5的时间分布与演变扩散[5].

南京市作为长江三角洲辐射带动中西部地区发展的重要门户，近几年经济得到迅速发展，高能耗企业频出，人口密集进一步加大，城市建设与环境保护之间的矛盾日益加剧.2013年12月4日南京首次发布霾红色预警，与此同时，南京市气象部门统计数据显示，2013年南京市有242天出现霾，即南京全年有五分之三的时间处于雾霾之中，这一数据达到了有气象统计以来的最高值[6].据2014年南京市环境状况公报显示，南京市环境空气质量超标天数高达175天[7]，约达全年天数的半成，再一次敲响了南京市PM2.5防治的警钟.为此本文利用南京市2014年PM2.5日浓度时间序列，基于ARMA模型对南京市PM2.5浓度进行分析和预测，以期为南京市当前和未来的PM2.5防治工作提供第一手参考资料.

1ARMA模型的理论介绍及建模步骤

1.1ARMA模型的理论介绍

ARMA(Auto Regressive Moving Average Model)自回归滑动平均模型，是一种随机时序模型，由美国统计学家Box、英国统计学家Jenkins一起创立，因此简称为B-J方法[8].作为一种时序短期预测方法，其具有较高的精度，通常写为ARMA(p, q)，基本公式如下：

Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q

(1)

其中，{εt}是白噪声序列，φ1,φ2,…,φp为自回归系数，θ1,θ2,…,θq为移动平均系数，都是模型的待估参数.显而易见，AR(p)模型和MA(q)模型均为ARMA(p,q)模型的特殊情况.当公式(1)中q=0时，则是自回归模型AR(p)，当公式(1)中p=0时，则成为移动平均模型MA(q).

以上模型针对的是平稳序列，然而非平稳序列，需要经过差分变换转化为平稳序列后才能应用于ARMA模型.此时需要在公式(1)中引入滞后算子B，得到公式(2)：

φ(B)Xt=θ(B)εt

(2)

1.2时间序列特性的分析工具与方法

(1)序列的平稳性检验

如果时间序列{Xt},t∈N满足：

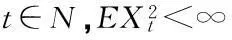
②对任何t∈N,EXt=μ；对任何t,s∈N,E[(Xt-μ)(Xs-μ)]=γt-s，就称{Xt}是平稳时间序列，简称平稳序列.

针对获取的时间序列，在建立模型之前，通常需要对其进行平稳性检验，其中ADF检验法运用最为广泛，下面对ADF检验法进行简要说明：

首先，假定序列{Xt},t∈N服从AR(p)过程.检验方程为：

▽Xt=γXt-1+ξ1▽Xt-2+…+ξp▽Xt-p+1+εt

其中，εt是白噪声，若参数γ<0，则序列是平稳的，而当参数γ=0时，序列至少存在一个单位根，序列是爆炸性的，没有实际意义.因此ADF检验的原假设可以表示为：H0:γ=0H1:γ<0.

其次，构造ADF检验统计量：

(3)

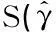
通过公式(2)可以计算得到一个t统计量，然后通过查询ADF检验统计量的临界值表，决定是否拒绝原假设.如果计算得到的t统计量绝对值超过ADF检验的临界值，则拒绝原假设，认为序列是平稳的，反之，则认为序列是非平稳的.

(2)ARMA模型的识别

ARMA模型的识别其实就是对模型进行定阶，确定p、q的取值，常用的方法有序列的自相关图和偏自相关图、AIC准则.

首先，通过对平稳序列的自相关图和偏自相关图进行分析，有如表1所示的模型识别依据[9]：

表1　ARMA模型识别依据

当运用自相关图和偏自相关图难以确定阶数时，再采用AIC准则进行判断.针对某一p、q取值，当AIC(p, q)取最小值时，p、q为最佳的模型阶数，此时模型达到最优.

1.3ARMA模型的建模步骤

Box-Jenkins提出了针对时间序列的建模思想，其建模基本步骤如下：

(1)检验原始序列进行平稳性，若序列表现为不平稳，可对序列进行差分变换使其达到平稳；

(2)求出该观察值序列的样本自相关函数和样本偏自相关函数，结合AIC准则，选择适当p、q拟合ARMA(p, q)模型；

(3)运用OLS估计ARMA(p, q)模型中的未知参数；

(4)检验模型的合理性，当拟合模型无法通过检验时，需返回步骤(2)，重新确定p、q；

(5)模型优化，即时拟合的模型通过检验，仍然可以返回步骤(2)重新确定p、q来模型进一步优化，从而选取最优模型；

(6)根据最终确定的拟合模型，预测序列的未来趋势.

2南京市M2.5浓度的实证分析与预测

通过中国空气质量在线监测平台选取南京市2014年1月1日至12月31日PM2.5浓度数据[9]，共365个样本.下面旨在利用ARMA模型的建模理论结合EViews7进行南京市PM2.5浓度的实证分析与预测.

2.1原始数据平稳性检验

首先，运用EViews7画出南京市2014年1月1日至12月31日PM2.5浓度时间序列图，如图1所示，通过对时序图的分析，可以大致认为该序列没有明显的趋势，初步判断序列是平稳的.

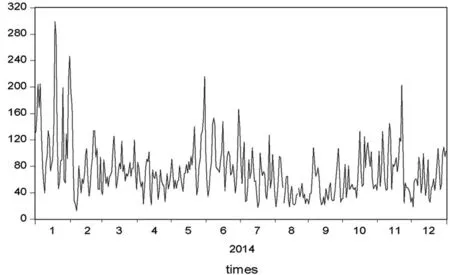
图1　PM2.5浓度时间序列图

接下来，采用ADF检验对原序列进行平稳性检验，若数据没有通过检验，则说明原始序列不平稳.运用EViews7继续ADF检验，结果如表2所示.

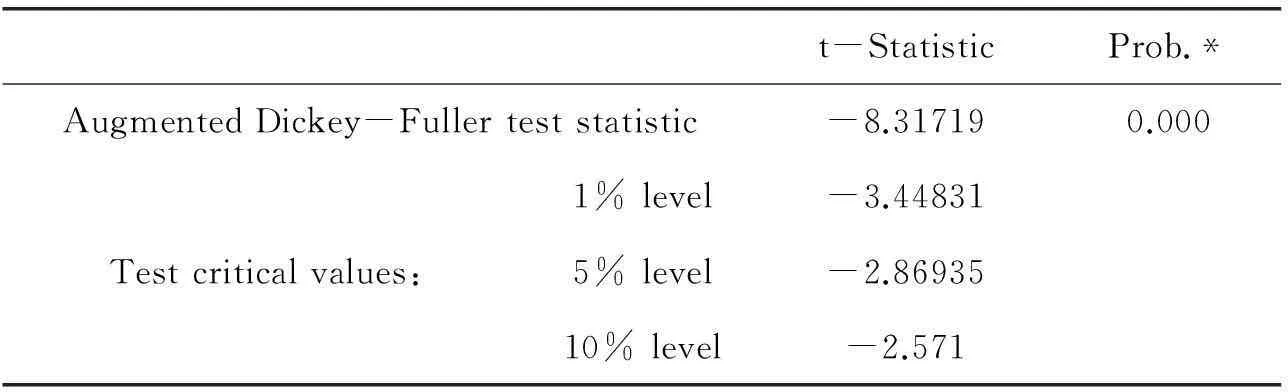
表2　序列PM2.5的ADF检验结果

ADF检验的原假设为序列PM2.5存在一个单位根，由表2知，ADF检验的t统计量值为-8.32，比1%显著性水平临界值-3.45要小，因此在99%的置信水平下，可以拒绝原假设，认为序列PM2.5不存在单位根，即序列平稳.

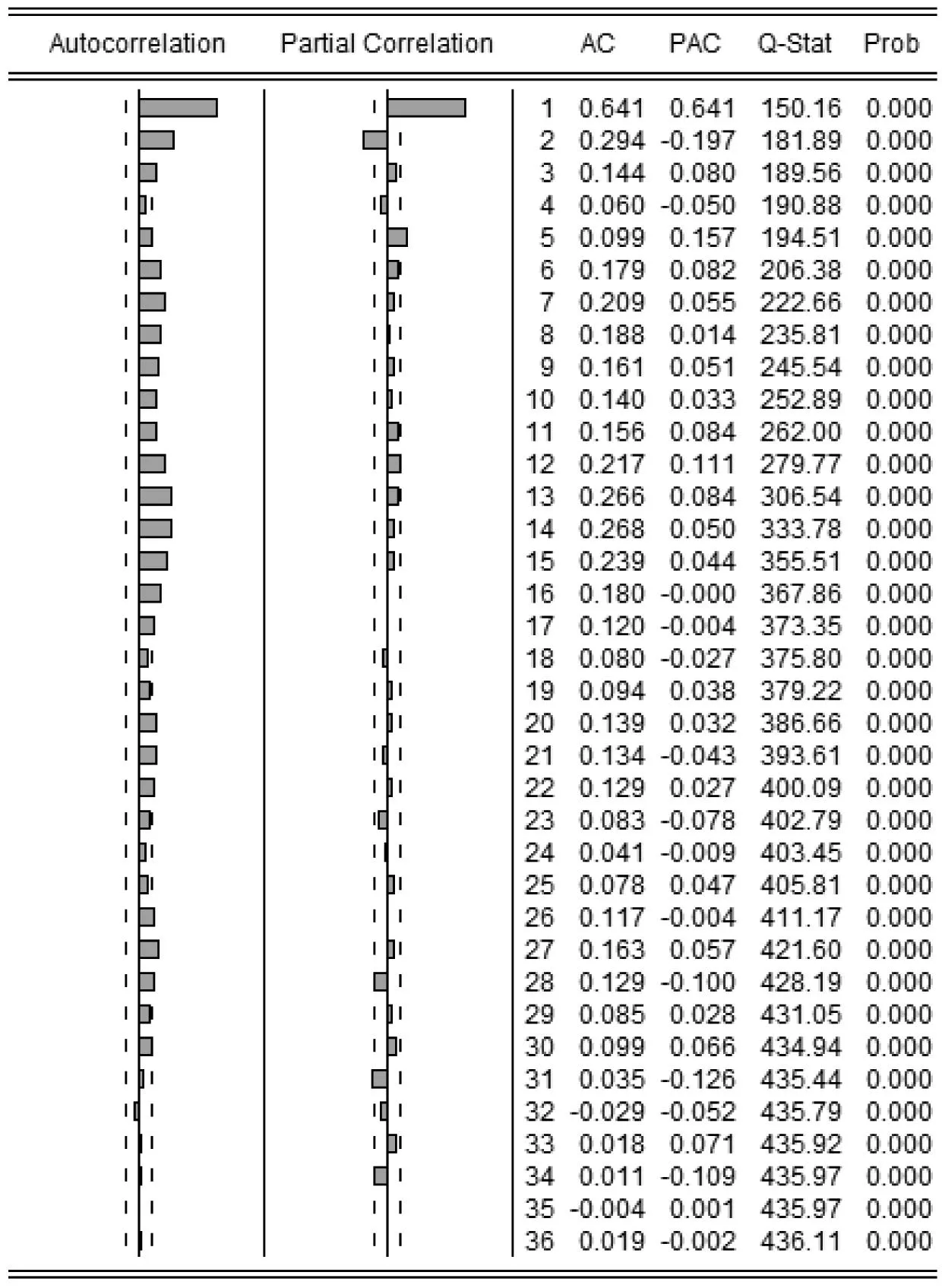
图2　PM2.5序列自相关—偏自相关分析图

2.2模型识别

运用EViews7画出原始序列的自相关图和偏自相关图，如图2所示，接下来，通过分析图2进行模型的识别和定阶.

总观图2，可以看出，原始序列的自相关图和偏自相关图都没有明显的截尾性，因此需要尝试使用ARMA模型.首先，通过观察图2左边的序列自相关图，可以看出序列明显地短期相关，延迟1阶、2阶、3阶以及5阶的相关系数均显著不为0，延迟4阶的相关系数近似为0；且序列相关系数由非零衰减为小值波动的过程较为连续和缓慢，因此可以判定该序列的自相关系数具有拖尾性，可以考虑取q=2或q=3.再观察图2右侧的序列偏自相关图，可以看出偏自相关系数除了在延迟1阶、2阶以及5阶时显著大于2倍标准差，其他延迟阶数时，基本在2倍标准差范围内，因此，可以考虑P取5.

综上，本文可以对PM2.5序列建立ARMA(5,2)模型或者ARMA(5,3)模型.

2.3模型的参数估计

确定模型的阶数后，需要对模型进行参数估计.

表3ARMA(5,2)模型参数估计及检验结果

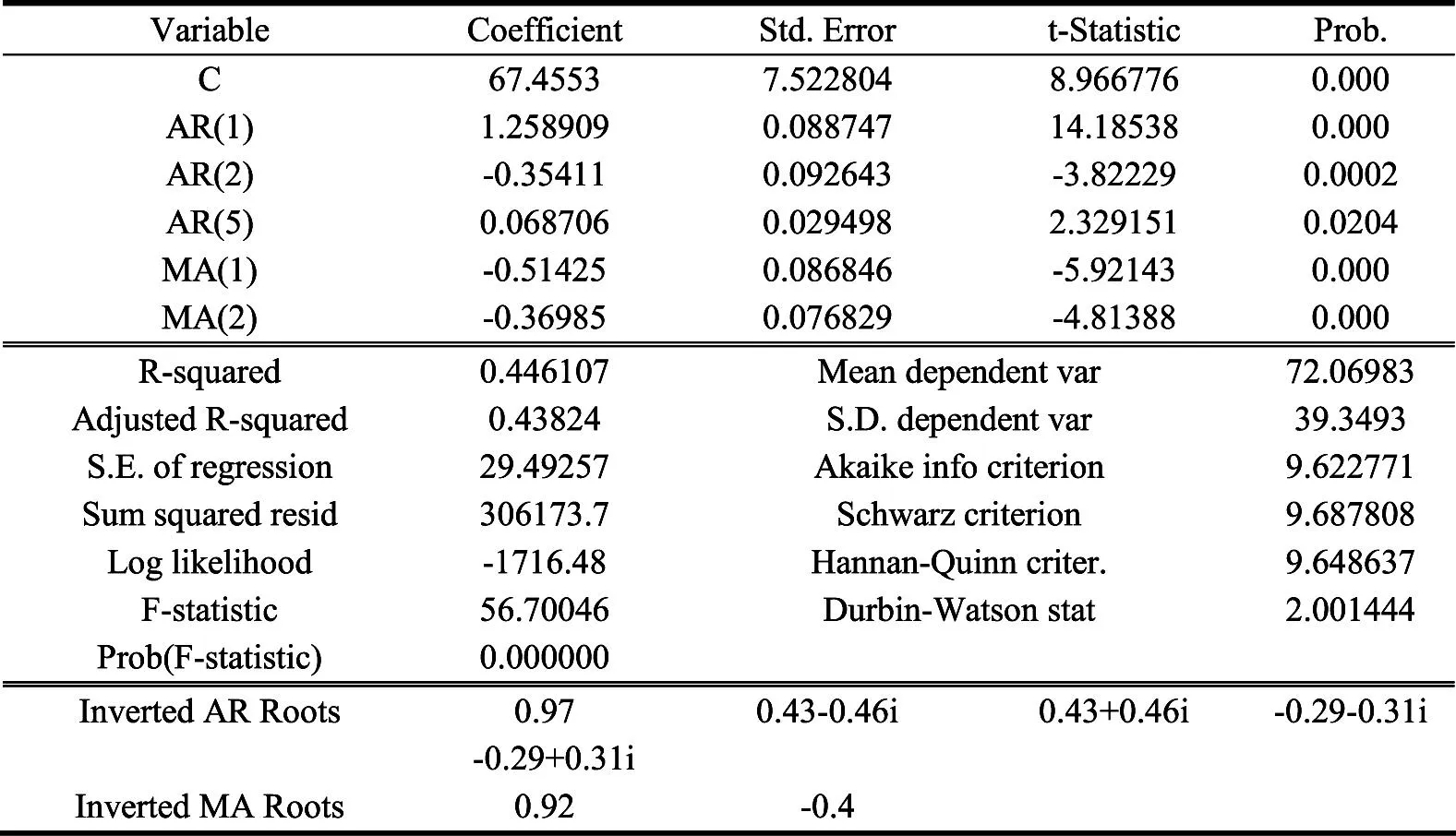
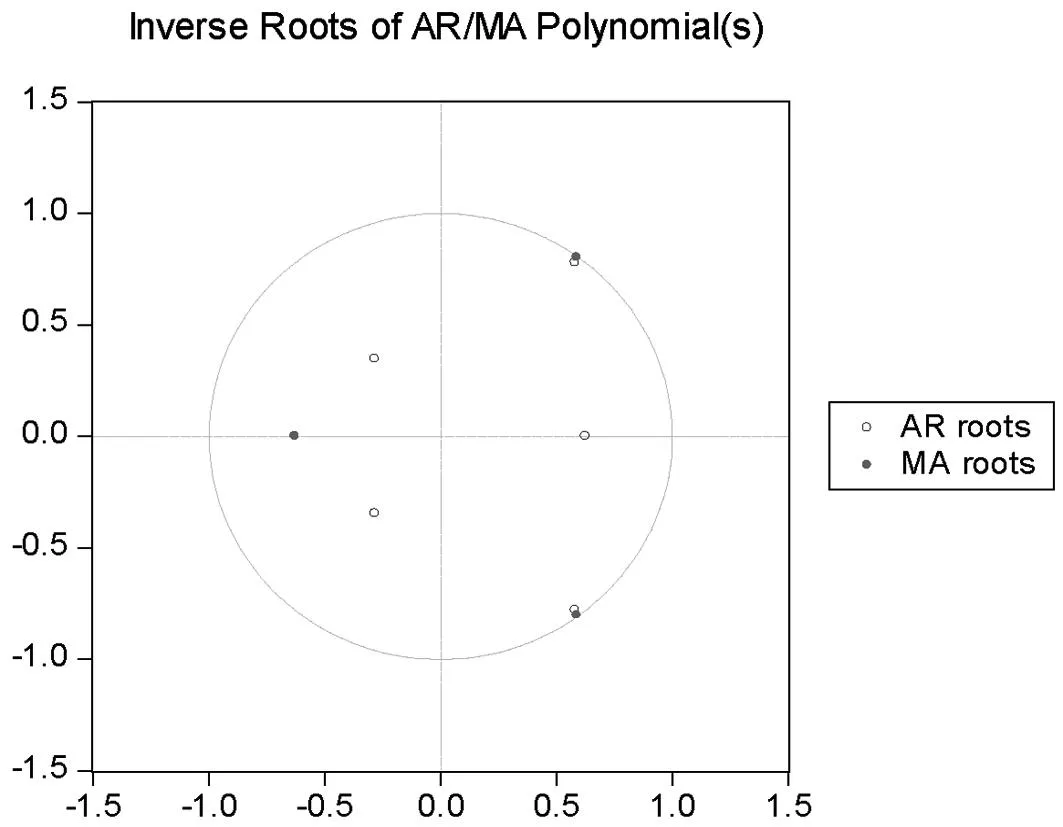
图3　单位根检验

运用EViews采用非线性方法分别对ARMA(5,2)和ARMA(5,3)模型进行参数估计与检验，结果分别如表3和表4所示，两表上部分与普通最小二乘估计结果一样.此时需要根据模型调整后的可决系数以及AIC和SC准则等判断模型的整体拟合效果.两表中最下面三行均为滞后多项式φ(x-1)=0和θ(x-1)=0的倒数根，当倒数根都位于单位圆之内时，即可判定过程是平稳的.由图3可知，表3和表4中的根都在单位圆内，均符合要求.

表4ARMA(5,3)模型参数估计及检验结果

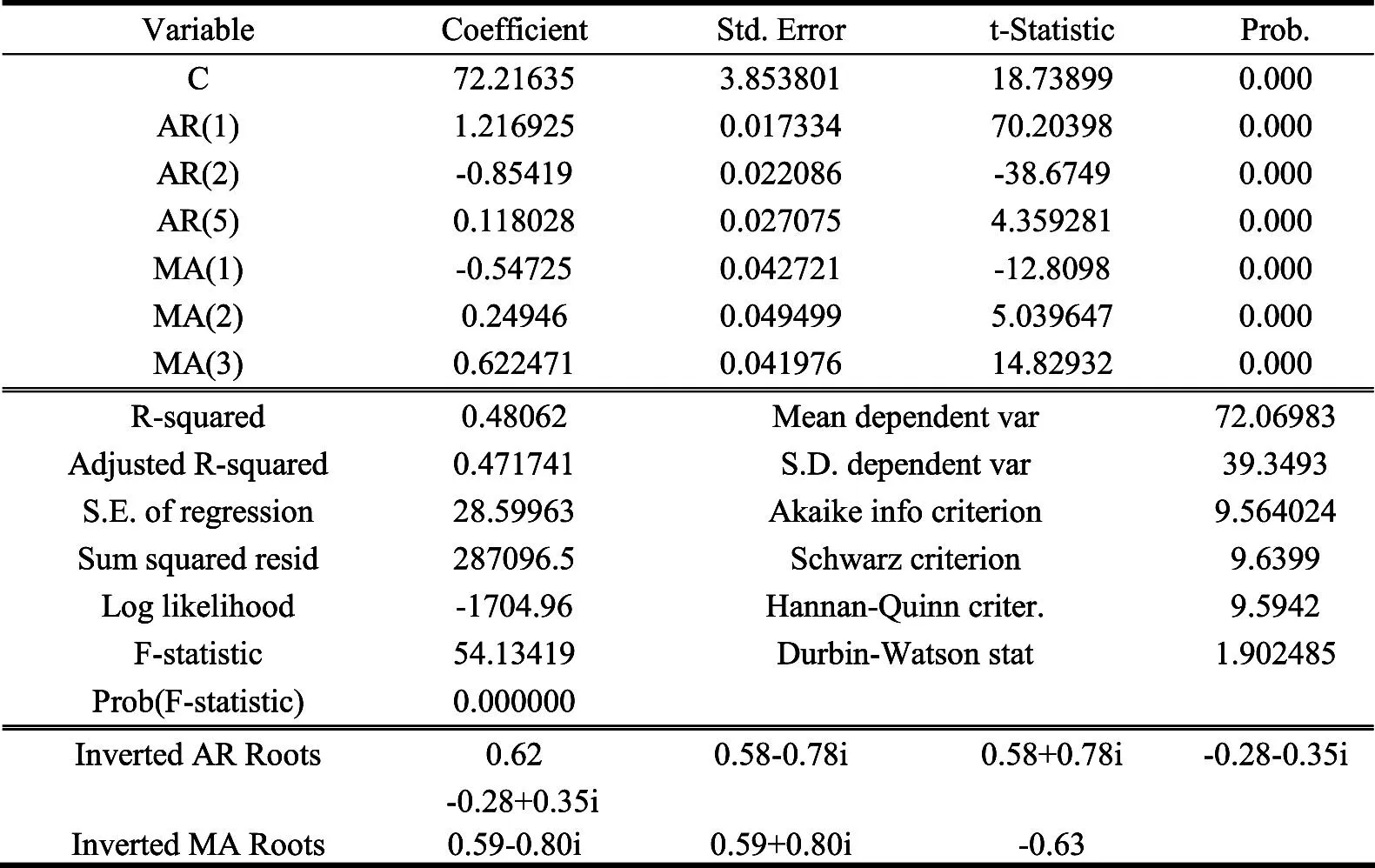
由表4可知，ARMA(5,3)模型调整后的R2为0.471741大于表3中ARMA(5,2)模型的0.43824，而AIC和SC值分别为9.564024和9.6399，分别小于表3中的9.622771和9.687808，因此认为ARMA(5,3)模型更合适，其对应的模型表达式为：

Xt=1.28Xt-1-0.36Xt-2+0.07X5+εt+0.52εt-1+0.37εt-2

2.4模型的检验

参数估计后，还需要进一步检验残差序列et是否为白噪声，即当滞后期k≥1时，et的样本自相关系数是否大致为0.当残差序列不是白噪声时，表明残差序列中还有少量有用信息没有被提取出来，此时需要对模型进行改进.模型的检验一般侧重于检验残差序列的随机性，通过对残差序列进行χ2检验，可以大致判断其是否是纯随机序列.首先，给出残差序列的自相关函数：

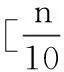
则接受原假设，认为模型通过检验，即残差序列{et}之间相互独立，；否在检验不通过[8].

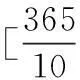
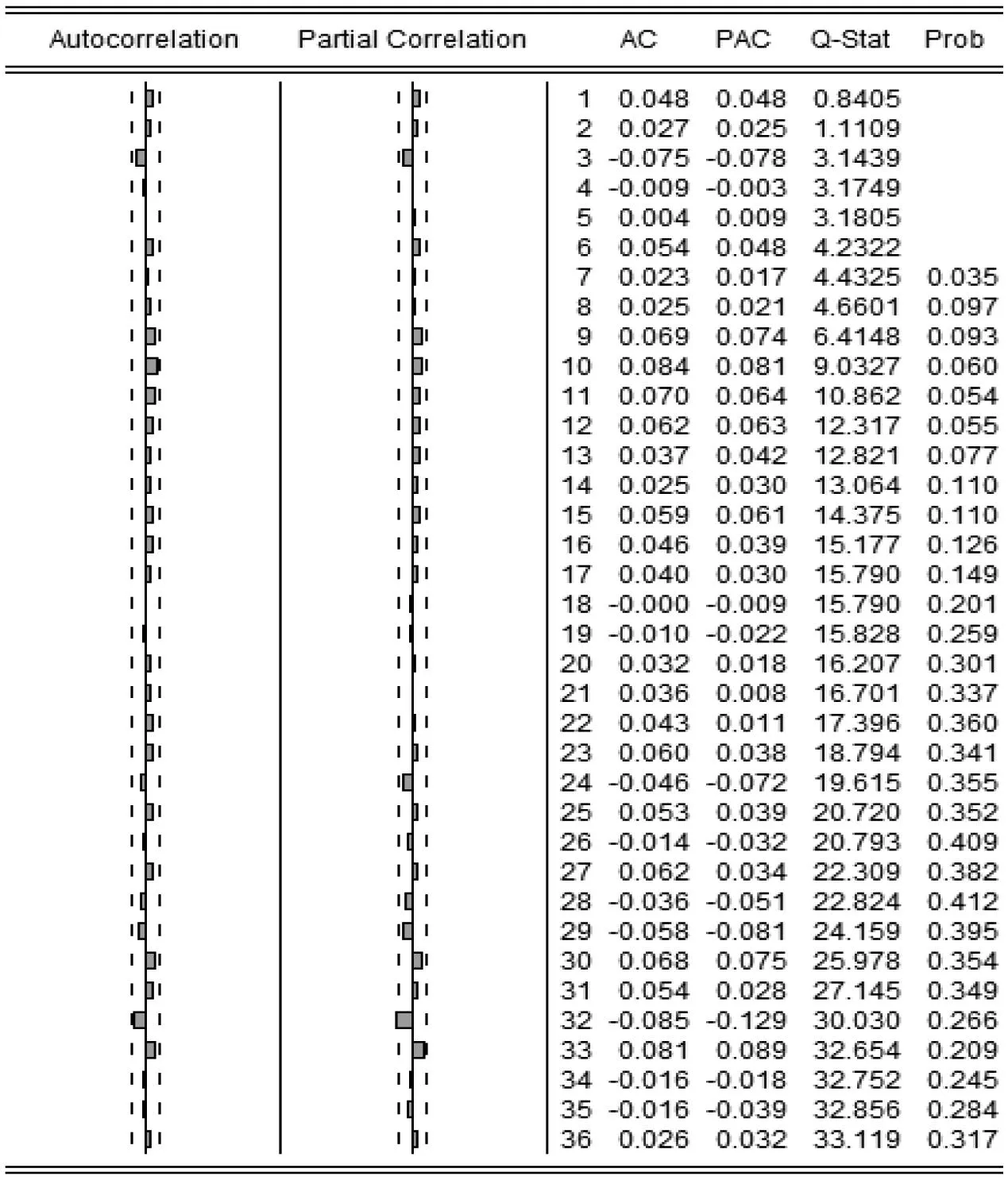
图4　ARMA(5,3)残差序列的自相关—偏自相关分析图

2.5模型的预测

接下来运用已经建立好的ARMA(5,3)模型，通过EViews7对南京市2014年1月1日至12月31日PM2.5浓度进行拟合，得到图5.

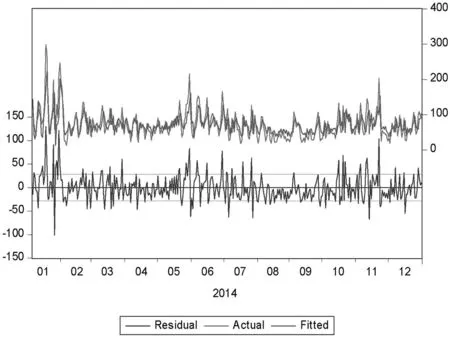
图5　南京市2014年1月1日至12月31日PM2.5浓度拟合预测效果

如图5，红色、绿色、蓝色曲线分别表示序列观察值、拟合序列值以及序列的残差.可以看出，拟合值与观测值十分接近，模型的拟合预测效果良好.

下面采用线性最小方差，利用ARMA(5,3)模型对PM2.5序列的未来发展进行预测，给出2015年1月1日至5日五天的预测值，如表5所示.

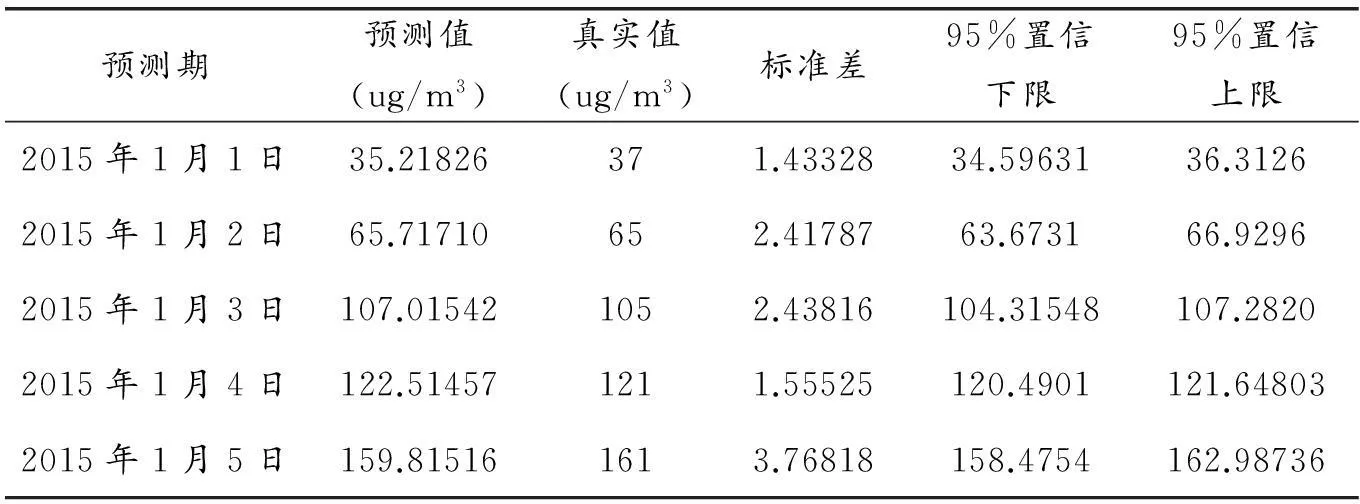
表5　2015年1月1日至5日南京市PM2.5预测值与真实值比较

从表中可看出，置信区间长度远远大于预测值与真实值的误差范围，所以本文建立模型的预测效果较好.由此也进一步验证了本文所建立模型的准确性，对目前空气中PM2.5预测具有较好的实际意义.

3结论

本文利用时间序列分析的Box-Jenkins建模思想，对南京市2014年1月1日至12月31日PM2.5浓度这一时间序列进行模型的建立和实证分析，得到符合南京市PM2.5浓度变化的ARMA(5,3)模型，了解了南京市PM2.5变化的基本特征.

首先，针对原始数列进行平稳性检验得到原始数据基本平稳；其次，运用原始序列的自相关图和偏自相关图进行模型识别，确定可建立的模型为ARMA(5,2)和ARMA(5,3)；然后，对两个模型进行参数估计与检验，确定合适的模型为ARMA(5,3)，并根据参数估计结果给出模型的表达式；随后，对已识别的模型进行检验，充分验证了所设计模型的合理性；最后，运用已经确立好的模型，对南京市2014年1月1日至12月31日PM2.5浓度进行拟合，通过与实际值进行比较，再一次验证了模型的准确性，并对南京市2015年1月1日至5日的PM2.5浓度做了短期预测，发现模型具有较好的预测效果.

综上所述，ARMA模型较好地解决了大气中PM2.5的时间分布问题，借助EViews软件能够十分便捷地将ARMA模型应用于大气中PM2.5浓度的分析与预测，为国家和地方政府进行空气质量监测、预报、控制以及制定相应政策、法规和管理办法提供决策指导.

参考文献

[1]国家发展改革委环资司.节能减排形势严峻产业发展潜力巨大——2013年上半年节能减排形势分析[J].中国经贸导刊.2013:14-15.

[2]杨凌宵.济南市大气PM2.5污染特征、来源解析及其对能见度的影响[D].山东大学,2008.

[3]刘辉,贺克斌,巧水亮,等.2008年奥运前后北京城、郊PM2.5及其水溶性离了变化特征[J].环境科学学报.2011,31(1):177-185.

[4]张振华.PM2.5浓度时空变化特性、影响因素及来源解析研究[D].浙江大学,2014.

[5]卢鹏,何杰.PM2.5的时间分布与演变扩散研究[J].西南民族大学学报2014,40(1):66:70.

[6]中国新闻网.去年南京雾霾242天“防霾”成南京两会热议词[2015-11-2].http://www.chinanews.com/sh/2014/01-12/5725911.shtml.

[7]南方日报.2014年南京市环境状况公报.[2015-11-2].http://njrb.njdaily.cn/njrb/html/2015-06/05/content_158622.htm.

[8]易丹辉.数据分析与EViews应用[M].北京:中国统计出版社,2002.

[9]冯盼,曹显兵.基于ARMA模型的股价分析与预测的实证研究[J].数学的实践与认识2011,41(22):85-89

[10]中国空气质量在线监测平台[2015-10-31]. http://www.aqistudy.cn/.

[责任编辑：房永磊]

PM2.5 Concentration Analysis and Prediction in Nanjing Based on ARMA Model

LIU Ling, SONG Ma-lin*

(Anhui University of Finance and Economics Institute of Statistics and Applied Mathematics, Bengbu 233030,China)

Abstract:In connection with PM2.5 concentration in different time, use PM2.5 concentration of everyday in Nanjing in 2014, apply Box-Jenkins time series analysis modeling ideas, combined EViews7, get ARMA (5,3) model conform with the changes ofPM2.5 concentration in Nanjing and predict the concentration of PM2.5 from January 1, 2015 to 5th, by contrast with the actual data and found that the model has better fitting, is suitable for the analysis and prediction of PM2.5 concentration in the atmosphere.

Key words:PM2.5; time series; eviews7; ARMA model; prediction

[中图分类号]X511

[文献标识码]A

[文章编号]1004-7077(2016)02-0054-09

[作者简介]宋马林(1972-)，男，安徽蚌埠人，安徽财经大学统计与应用数学学院教授，硕士生导师，主要从事资源环境统计、数量经济的研究.

[基金项目]安徽省级创新创业项目(项目编号：AH201410378516).

[收稿日期]2016-02-01