一道模拟题的加强与改编*——兼谈零点存在定理应用的新视角



一道模拟题的加强与改编*
——兼谈零点存在定理应用的新视角

厦门大学附属实验中学(363123)田富德

对数学试题的探究、改编可以有效促进数学教师的自身解题能力，提高数学教师的解题教学水平．解题与命题相互促进，其一，命题者可谓知其然又知其所以然，故命题者可以站在解题的至高点进行解题;其二，只有通过一定量的解题和对试题的深入探究思考，才能促进数学教师的命题水平．因些，中学数学教师对一些精彩的模拟试题、高考试题进行深入探究思考，方能提高自身的命题能力，站在解题的至高点引领学生破解各类创新试题．

1.原题及参考答案展示

试题来源徐州、淮安、宿迁、连云港四市2015届高三第一次模拟考试第20题．

(Ⅰ)(Ⅱ)略;

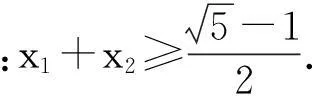
参考答案：(Ⅰ)(Ⅱ)略;

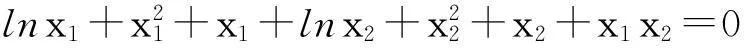
2.试题的加强及解法

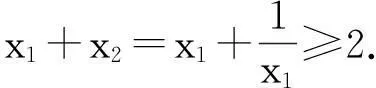
于是，我们可以将试题进行加强，得到如下：

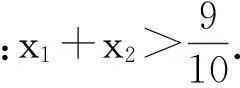
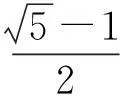
我们可以进一步提高试题的难度，得到如下：

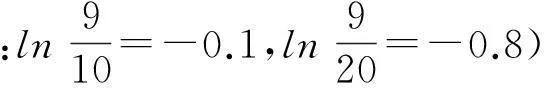
分析：本题等价于求x1+x2的取值范围，我们可以设x1+x2=t，然后利用零点存在定理研究方程解的问题，来分析符合题意的t值．

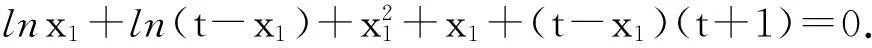
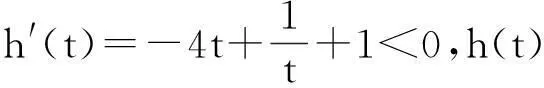
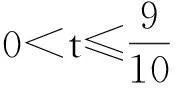
3．解题策略

双变量满足某函数方程，求解双变量线性表达式的范围问题，我们可以归纳如下几步：

第一步，设双变量x1,x2的线性表达式αx1+βx2=t;

第二步，将其中一个变量x1(或x2)用另一个变量表示，代入双变量所满足的函数方程;

第三步，视t为常量，x1(或x2)为变量构造函数g(x)，转化为研究函数g(x)的零点问题．解题的本质是引入参数，消去变量之一，构造函数，利用零点存在定理来解题．

4．策略应用

例(2010年高考数学天津卷理科第21题改编)已知函数f(x)=xe-x(x∈R)．

(Ⅰ)求函数f(x)的单调区间及极值;

(Ⅱ)略;

(Ⅲ)如果x1≠x2，且f(x1)=f(x2)，求x1+x2的取值范围．

分析：利用文[1]、文[2]的解法均可以轻松证明x1+x2>2，但均未能说明2为x1+x2的下确界，以下利用零点存在定理来求解x1+x2的取值范围．

解析：(Ⅰ)(Ⅱ)略;

(Ⅲ)不妨设x11．由条件知f(t-x2)=f(x2)，即x2e-x2+(x2-t)ex2-t=0(max{(t-1),1}

参考文献

[1]邢友宝．极值点偏移问题的处理策略[J]．中学数学教学参考：上旬，2014(7)：19-22．

[2]赖淑明．极值点偏移问题的另一本质回归[J]．中学数学教学参考：上旬，2015(4)：49-51．

*本文系2015年度漳州市基础教育课程教学研究立项课题《高中数学解题教学现状与优化》阶段性研究成果.