一个对称不等式的另证及两个不等式二次推广



一个对称不等式的另证及两个不等式二次推广

四川省南充高级中学(637000)张小丹

数学通讯2008年三月号问题1724：

文[1]和文[2]分别用了高、初等数学的方法对该命题进行了证明，特别地，文[2]的两位老师还对文[1]给出的两个推广命题作了修正，得到推广1与推广2，如下：

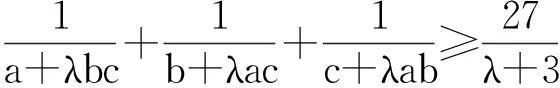
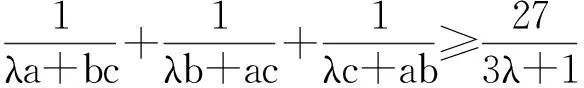
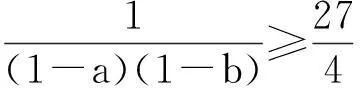
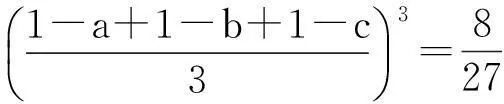
本文的方法较自然，流畅，但是我接着会发现，此法无法应用于上述两个推论的证明，于是我又不断尝试寻找另法.

二、两个推广命题的另证

先证推广命题1. 观察分母之和为a+b+c+λ(ab+bc+ac)=1+λ(ab+bc+ac)，而ab+bc+ac与a+b+c之间又存在一个大小关系，于是我们把这里作为一个突破口.

为了后续证明的方便，我们先给出

引理1若a,b,c>0,且a+b+c≤s，则有

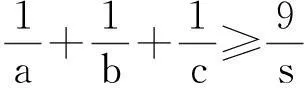
下对推广1进行证明：

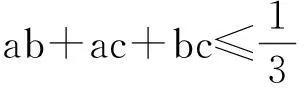
对于推广2，我们采用类似方法.

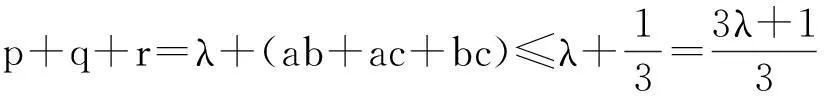
三、对两个推广命题的二次推广

推广1、2中恒成立的不等式含有三个数，那么能否将其推广到含有n个数的情形呢？经过探究，我发现这一猜想是可行的.

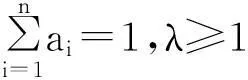
为了方便后续证明，我们先给出

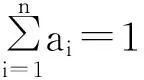
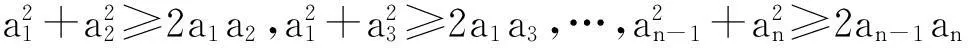
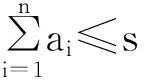
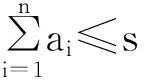
以下对推广3进行证明：

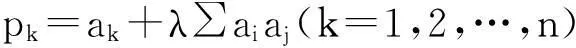
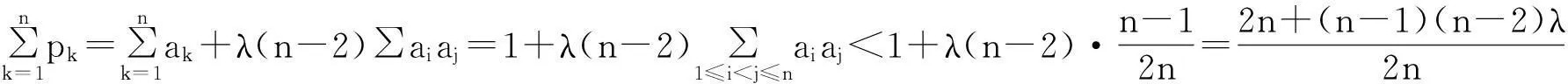
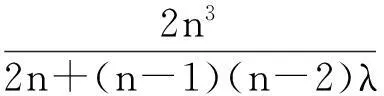
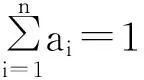
对推广4的证明可参考推广2，同时结合引理2、3，有兴趣的读者可以自己感受一下.

参考文献

[1]赵克,赵临龙.对称不等式的证明及命题推广[J].中学数学研究(江西).2013,7.

[2]马占山,潘长江.一个对称不等式的简证及两个命题修正[J].中学数学研究(江西).2014,5.