一类绝对值不等式问题的再思考
2016-05-11胡志杰,吕孙忠,吴云浪
一类绝对值不等式问题的再思考
浙江省湖州二中(313000)胡志杰
北京师范大学研究生院(100875)吕孙忠
浙江省永嘉中学(325100)吴云浪
综观近年数学高考和自主招生考试,不等式试题越来越趋向于对绝对值不等式的考查.解决绝对值问题最常规的方法便是“分类讨论”,只要有足够的时间,“分类讨论”总能解决问题,但前提是有足够的时间.其实绝对值有它得天独厚的几何意义,即数轴上两点之间的距离.因此在解决该类题型时,解题方法的选择显得尤为重要,选择不当,费时、费力,且不得要领,选择恰当,便可“投机取巧”,秒杀考题.
文[1-2]对一道自主招生中的不等式试题进行了探究,但它们所涉及的绝对值前的系数都是正整数,笔者从一道高考题谈起,将前置系数从正整数域推广至实数域,并得到若干推论.
1巧用数轴,妙解最值
题源(2014年安徽数学高考理科第9题)若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值().
A.5或8B.-1或5C.-1或4D.-4或8
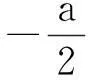
下面给出一种妙解:
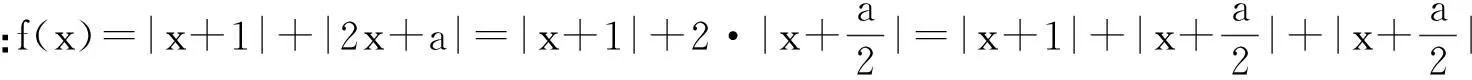
2探索最值,追根溯源
首先,需要介绍一个应用比较广泛的,关于绝对值不等式最值的引理.
引理若f(x)=|x-a|+|x-b|+|x-c|(a≤b≤c),当且仅当x=b时,f(x)min=f(b)=|a-b|+|c-b|=c-a.[3]
同时,推广引理,可以得到n维形式的结论.
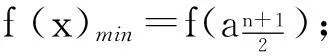
推论2 f(x)=n1|x-a1|+n2|x-a2|(a1≤a2),n1,n2∈N+.若n1>n2,f(x)min=f(a1);若n1≤n2,f(x)min=f(a2).
推论3 f(x)=m1|x-a1|+m2|x-a2|(a1≤a2),m1,m2∈Q+.若m1>m2,f(x)min=f(a1);若m1≤m2,f(x)min=f(a2).
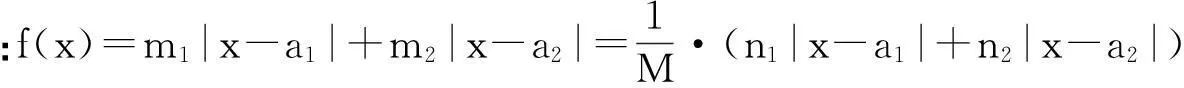
推论4f(x)=n1|x-a1|+n2|x-a2|+…+nk|x-ak|(a1≤a2≤…≤ak),n1,n2,…,nk∈N+.若n1+n2+…+ni
注:推论4是推论3的推广形式,同时,可以将推论4的结论推广到有理数域上,得到推论5.
推论5f(x)=m1|x-a1|+m2|x-a2|+…+mk|x-ak|(a1≤a2≤…≤ak),m1,m2,…,mk∈Q+.若m1+m2+…+mi
推论1到推论5都是在前置系数符号为正的前提下得到的,若系数都是负数的话,可以得到一个绝对值函数求最大值的结论.
推论6f(x)=m1|x-a1|+m2|x-a2|+…+mk|x-ak|(a1≤a2≤…≤ak),m1,m2,…,mk∈Q-.若m1+m2+…+mi
注:当mj(j=1,2,…,k)都为负有理数时,那么在整个式子前,添加个负号,那么问题就转化成了求最大值问题.
3例题示范,结论推广
巧用以上推论,可以秒杀一系列高考不等式考题及竞赛题型.
例1(2008年“希望杯”高二试题)如果对任意实数x,都有|x-1|+|x-2|+…+|x-2008|≥m成立,那么m的最大值是().
(A)1003×1004(B)10042
(C)1003×1005(D)1004×1005
分析:例1可用推论1直接秒杀.
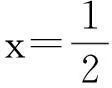
例3(2007年全国高中联赛题)不等式|2x-a|+|3x-2a|≥a2对∀x∈R恒成立,则满足条件的实数a组成的集合为().
分析:本题实质与例2无异,是推论3的直接使用.
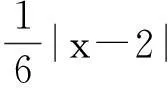
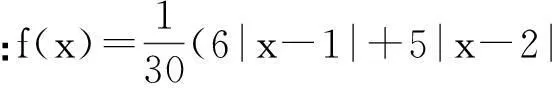
例4(2011年“北约”自主招生压轴题)求f(x)=|x-1|+|2x-1|+|3x-1|+…+|2011x-1|的最小值.
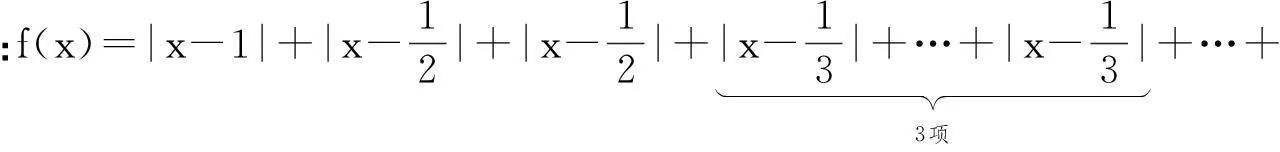
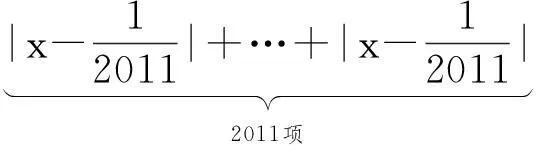
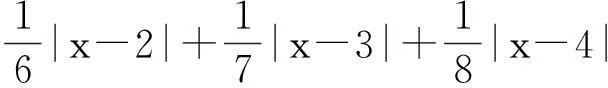
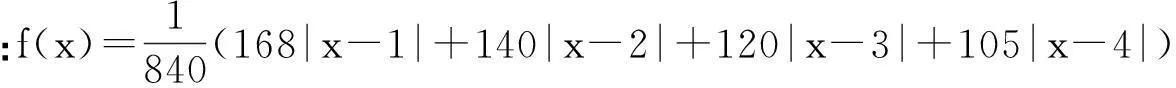
4推论延续,反思小结
以上涉及的例题和推论,其绝对值前的系数都还是限制于有理数域内,如果我们将命题推广到实数域上,那么绝对值前的系数是无理数的时候,命题还成立吗?答案是显然的,因为我们可以用有理数去无限逼近无理数.
用绝对值的“距离”意义解决相关试题,还有更多的案例,限于篇幅,不再举例.可是,笔者所提到的方法,并不是追求高难度的解题技巧,而是着意于解题工具的选择,着意于数学问题的理解,揭示数学本质,看出题目的结果.在实际操作中,读者需将其与“分类讨论”双管齐下,方可所向披靡.最后,笔者再提出一个思考问题.
思考文中推论里的绝对值前置符号都是一致的,都是正号时可以求函数的最小值,都是负号时可以求函数的最大值,那么,如果函数前置的正负符号混合时,会有怎么样的结论?
参考文献
[1]范端喜. 一道“北约”自主招生绝对值不等式问题的探究[J]. 数学通讯,2013,10:56-58.
[2]刘再平. 一道“北约”题的推广、变式及溯源[J]. 中学生数学,2013,13:40-41.
[3]李胜宏,李名德.高中数学竞赛培优教程[M].浙江大学出版社,2012.
