对一次试卷讲评课的一点感悟



对一次试卷讲评课的一点感悟

江西省南昌三中(330008)张金生

通常，试卷讲评课要力求精讲精析，抓住典型的错例，择其要点加以点拨，充分启发学生思考，对重要的解题思维和方法进行有效的归纳与训练.在此基础上，还应鼓励学生开动脑筋，引导他们对典型试题进行反思与总结，通过归纳、类比、展开联想进行迁移或拓展，挖掘试题中的潜在性质，将进一步激发学生的学习兴趣，培养学生创新能力，提高试卷讲评课的效果.

在学校的一次月考中，解析几何解答题是2014年高考广东卷20题：

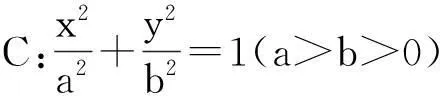
(1)求椭圆C的标准方程;(2)若动点P(x0,y0)为椭圆C外一点,且点P到椭圆的两条切线相互垂直,求点P的轨迹方程.

在讲评完该题后，笔者提出问题：“对于该题能否提出一般性的结论？请同学们思考，明天上课时就请同学来讲”.

这一同学的讲解和回答得到了师生给予肯定和赞扬.

在随后一周的周练试卷上我特意出了这样一道解析几何解答题：

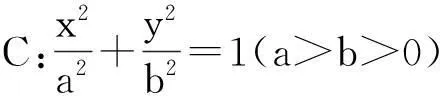
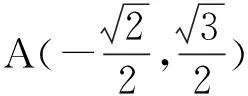
(1)求椭圆C的标准方程；

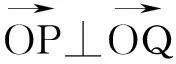
在这次的试卷讲评课中，我特意引导同学回顾对比上次的月考题，要求同学给出一般结论，同学们恍然大悟，原来椭圆的“小伴随圆”在这里！

通过这次对椭圆“伴随圆”的发现与探究，同学们感到圆锥曲线问题很神奇，奥妙多！大大激发了同学们学习数学的热情，也提高了同学的科学探索兴趣.

实际上，试卷讲评课的目的不仅仅是纠正错误,巩固知识,试卷讲评的内容也不应是学生已学知识的简单重复，必须有所变化与创新.试卷讲评课中教师应抓住课堂生成，引导学生课后反思和拓展，充分发挥学生的主观能动性,放手让学生大胆地去想、去做、去说，只有这样学生才能体验到成功的喜悦，才能勇敢地提出各种各样的问题和解法；也只有这样才能培养学生具有创新意识、创新精神及创新能力.由此获得试卷讲评课的育人成果.