挖掘教材 超越教材*——由一道学考题引发的教学思考

●叶晓武　(永嘉中学　浙江永嘉　325100)



挖掘教材超越教材*——由一道学考题引发的教学思考

●叶晓武(永嘉中学浙江永嘉325100)

摘要:做好对教材的挖掘和探究，是走向学习数学、学会数学学习的重要渠道．由此借助2014年7月浙江省高中数学学考题的呈现，分析考题源头，挖掘命题高度，理解问题本质．以学考题教学为例，总结复习教学中做好对教材问题的背景和本质的挖掘，更要做好对教材的探究和超越．引导学生把握教材知识的本质，学会思考和探究，培养良好的数学学习习惯．

关键词:学考;教材;阿波罗尼斯圆;数学思考

1　缘起学考——从学考题的解答中发现学生学习中存在的问题

在2014年7月浙江省普通高中学业水平测试中，第33题(解答题的第3题)是一个中上档的题目，涉及到求轨迹方程、圆关于直线对称问题和圆与圆的位置关系的判断等数学知识，需要运用数形结合、等价转化等数学思想，考查学生的运算能力、逻辑推理能力和分析问题与解决问题的能力．本题满分8分，全省平均得分不到2分，大多数考生不能解决这个问题，不少考生在第2)小题中由于不能分析和看透问题的本质、缺乏灵活的分析与思考等数学基本素质而导致失分．这样的现象不禁引发笔者的深深思考，我们该如何做好平时的教学?如何培养学生的运算能力?如何提高学生分析和思考问题的数学素质?所谓授之以“鱼”，不如授之以“渔”．

例1在平面直角坐标系xOy中，点A，B的坐标分别为(－1，0)，(1，0)．设曲线C上任意一点P(x，y)满足|PA|=λ|PB|(其中λ＞0且λ≠1)．

1)求曲线C的方程，并指出此曲线的形状．

2)对λ的2个不同取值λ1，λ2，记对应的曲线为C1，C2．

①若曲线C1，C2关于某直线对称，求λ1，λ2的积;

②若λ2＞λ1＞1，判断2条曲线的位置关系，并说明理由．

(2014年7月浙江省普通高中学业水平测试数学试题第33题)

第1)小题重在考查求轨迹方程的“直译法”，它是求轨迹方程方法中最基本、最通用的方法，是考纲要求掌握的基础知识．第2)小题中的①考查圆关于直线对称的特性，若不能理解本质，就很难求解，甚至无从求解;②中考查了圆与圆位置关系判断的基本方法，但难处在于庞大的计算量，面对字母学生是“望而却步”．

针对全省平均得分情况，笔者通过对部分学校学生的调查，了解到最主要的失分在于第2)小题，大多数学生束手无措．其一:面对那么多的字母参数他们有心理上的畏惧，想做又不敢做;其次，一些学生感觉应该就是按常规的思路，但看到巨大的代数式就没有信心也没有能力继续做下去;再次，更多学生不能理解本问题，没有对问题做好本质的分析，找不到解题的思路，看到那么多的字母以致无从下手．通过以上的调查与分析，我们应该做好反思并改进我们的教学．

2　源于教材——从对教材的处理中发现教师教学中存在的问题

翻阅教科书可以发现，教材书上有好几处练习对本知识点做了编写考查:

出处1人教社A版《数学必修2》第124页B组第3题:已知点M与2个定点O(0，0)，A(3，0)的距离之比为，求点M的轨迹方程．

出处2人教社A版《数学必修2》第140页:信息技术应用——用“几何画板”探究点的轨迹:圆．其中的例题:已知P(2，0)，Q(8，0)，点M与点P的距离是它与点Q的距离的，用“几何画板”探究点M的轨迹，并给出轨迹方程．

出处3人教社A版《数学必修2》第144页复习参考题B组第2题:已知点M(x，y)与2个定点M1，M2距离的比是一个正数m，求点M的轨迹方程，并说明轨迹是什么图形(考虑m=1和m≠1 这2种情况)［1］．

笔者调查了部分一线数学教师，对于课本上的题目他们的处理方式主要是2种情况:1)布置给学生做，基本没校对;2)没有布置，因为现在有了配套作业本等课外辅助教学用书，书本上的作业基本没做．了解中发现，几乎没有教师对这几个题目引起重视，更谈不上研究．作为学生，他们更不可能主动去做这个题目，当然就不会研究．

书本如此多次出现这个问题，设置这个题目作为课后习题，那肯定不失它的重要性和价值所在．其次，在信息技术应用处用“几何画板”探究它，说明了教材引导我们对其中本质的挖掘．可许多教师却丢弃了其“精华”，辜负了书本编者的初衷，背道而驰．大多数教师都只是在做更多的“应试题”，进行“题海战术”．认为仅需掌握圆的基本知识就够，却忽视了对圆知识的深入思考、探究，缺少了对问题本质的挖掘，也丢失了教学生学会思考和探究问题的学习能力．这引起我们的思考:知识掌握了，技能学会了，我们能丢弃“数学思考”吗?

3　“圆”归教材——研读教材，把握数学本质，启发数学思考

对比学考题和书本习题，可以发现:试题来源于教材，但又不拘泥于教材．教材上这3个问题都是偏重求轨迹和轨迹方程，突出求轨迹方程的方法．细心挖掘，可以清楚地看到编者的意图:在出处2中要求学生用“几何画板”探究，这里的设计就提醒我们对此问题要深入挖掘．而学考题，它不但考查了求轨迹方程的基本方法，第2)小题更突出考查了学生对问题的分析，把握问题的本质，做到有的放矢，从而达到胸有成竹地完成后续的计算．此处的“圆”，就是数学上著名的“阿波罗尼斯圆”，这其中的内容丰富多彩．

由此告诉我们，对于教材上的知识和习题，我们不能只是完成了事，或对它置之不顾．近几年的高考命题趋势都体现了题目的来源离不开教材，但又不拘泥教材，这就要求教师要重视教材，用好教材，并挖掘好教材，超越教材．

3．1立足教材——挖掘整理，把握本质，归纳思考

下面，笔者以学考题引发的思考，在高三复习中所开设的一堂复习课为例，示范在高三复习教学中如何挖掘教材，达到让学生的知识技能得以提升的同时，也让学生的数学思考能力得到培养，让学生学会学习数学，学会研究数学，学会“渔”的能力．

例2［2］满足条件的△ABC 的面积的最大值是______．

(2008年江苏省数学高考试题)

学生的解法有如下几种(简略叙述):

解法1(三角函数法)设边长BC=x，则

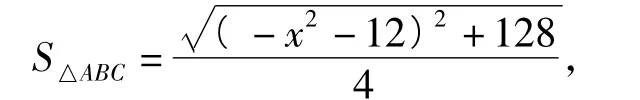
解法2引进角变量∠ACB=θ，得，从而求得最大值为

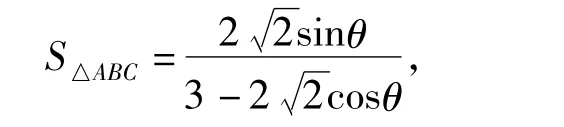
从而求得最大值．

解法3(解析法)应用“阿波罗尼斯圆”，将三角问题解析化．

设A(－1，0)，B(1，0)，动点C(x，y)，由AC=得

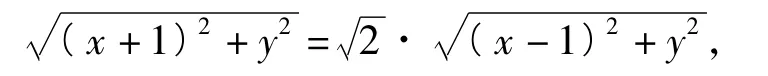
化简得

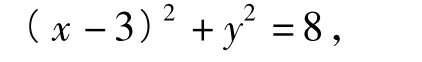
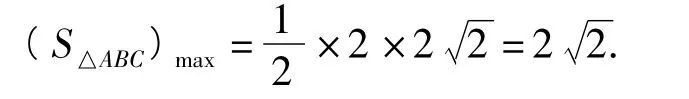
对比以上解法可以发现解析法对于此题的解决非常方便，这就是在“阿波罗尼斯圆”背景下解决问题．为此，若学生理解“阿波罗尼斯圆”的由来及其概念，也并非需要用相关结论来解决，只需做到“心中有数”，那就能快速解题．而这一切的成果源自平时教师对教材的挖掘和对学生的引导、启发，从而让学生把握本质，学会数学思考．

因此，若教师能在教材使用中，找到教材上的这3个问题，归类讲解，首先把这3个问题同时布置给学生当作业，校对讲解，然后进行拓展．可如下进行教学操作:

环节1布置作业——就是教材上的出处1和出处2这2个问题．

环节2作业校对讲解，归纳总结，把问题提升到得出“阿波罗尼斯圆”的概念．

环节3变式教学．

变式1在平面直角坐标系xOy中，点A，B的坐标分别是(－1，0)，(1，0)．设曲线C上任意一点P(x，y)满足|PA|=m|PB|(其中m＞0，且m≠1)．求曲线C的方程，并指出此曲线的形状．

变式2在平面直角坐标系xOy中，A，B是2个定点．设曲线C上任意一点P(x，y)满足|PA|= m|PB|(其中m＞0且m≠1)．求曲线C的方程，并指出此曲线的形状．

通过以上变式教学，让学生立足于教材，又高于教材，在解答教材习题的过程中，归结提炼出“特殊问题”中存在“一般结论”．这样的数学思考习惯，以及这样思考所获得的成就，学生一定能深刻掌握．这样让学生学会在解答数学问题的同时做到习惯性地“数学思考”，让数学知识和技能都得到提升，发展了他们学习数学的能力，培养了学习数学的好习惯，从而发现问题的本质，最终可谓是“会当凌绝顶，一览众山小”．

3．2活用教材——探究学习，启发思考，培养能力

显而易见，上面的变式教学其实只是让学生经历从“特殊”发现“一般”的结论．那到底是否理解其本质的内容?比值变化又有何区别?不同的比值间会有关系吗?这都是教师引导学生学习中要善于发现和思考的问题．很多文章也都对“阿波罗尼斯圆”做过研究，各国高考也都对“阿”进行考查，可他们都只是停留在对概念的考查，并没有对其中本质的挖掘．当然，我们的教学肯定不能只停留在知识和技能上，更应该教会学生学会“数学思考”，让知识变得透彻，让思维得以延续，让数学本质得以挖掘，启发学生学会数学思考．为此，笔者建议教学进行如下探究学习设计:

探究1你能快速画出上述的“阿波罗尼斯圆”吗?

学生探究发现，这个点的轨迹已经肯定是圆了，因此通过找特殊点M和N(在直线AB上)，其中这2个点只需要满足:

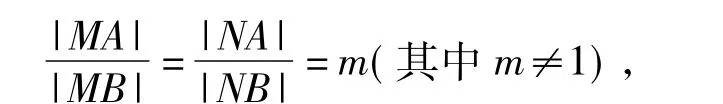
然后就以MN为直径画圆即可(如图1)．

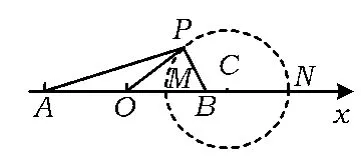
图1

在这个环节，学生采用了“特殊法”研究问题的思想，很快解决问题．这种思想在高考中也是探究一般性问题或是探索性问题的一种重要的研究思想，在此探究使用，让学生进一步体验和掌握此方法的重要．

这里的M和N其实就是内分点和外分点，而且∠MPN=90°，以此线段MN为直径作圆，这个圆即是所求圆．

探究2当m的值变化时，此时不同的阿波罗尼斯圆会有什么区别和联系?由此你能发现什么性质?

学生探究发现1m越大，点M越接近点B，点N也越接近点B，此时圆越小(因为直径MN在变小)．

学生探究发现2集合包含．从集合的角度观察，不同的m所对应的圆是包含关系，即

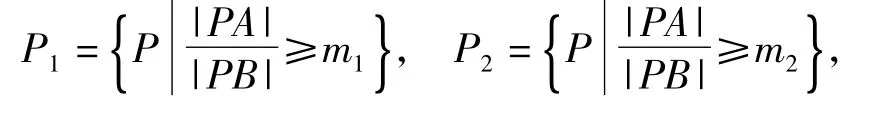
其中m1＞m2，若P∈P1，则P∈P2．

学生探究发现3对称性．由探究1学生发现比值m对图形的影响，因此动点P满足条件，可知2个圆关于线段AB的垂直平分线(y轴)对称．

由探究1和探究3的思考与发现，学生理解了比值m的意义，此时学考题第2)小题中①的答案“呼之欲出”，然后只用常规的坐标法加以验证．同样，对于第2)小题中②的答案也是顺应产生，这样的思考习惯，解题就轻松，当然也是命题者的初衷．

学生探究发现4由探究3学生的思维回到了熟悉的对数函数y=logax(其中a＞0且a≠1)与指数函数中的知识:当其中的a取2个相反的常数时，得到的函数图像关于y轴对称，这种知识类比的思维和迁移的思想能让学生具备更强的学习能力，学会更主动地思考问题．

通过以上的探究，学生不但掌握和落实了基本的求轨迹方程的方法，而且能站在更高的角度认识“阿波罗尼斯圆”，其中m的取值对图形的影响，不同m对应不同圆之间的区别和联系，而且通过探究4这个发现和类比，让学生体会到数学知识的奥妙、神奇和“豁然开朗”．毋庸置疑，这样的数学思考和探究，让学生在掌握知识技能的同时，更学会了数学思考，学会了学习和探究数学的思想方法，也培养了学生一种终身“会学习”的能力．

因此，学考和高考是我们教学的一个指导方向，而教材是一个基点．立足基点，朝着方向，我们可以清楚地看到考试的一个准则是:多考一点思考，少考一点计算;回归课本，超越课本．因此，在复习教学中，我们必须重视教材，因为教材是我们的教学工具，里面的题目是专家精心挑选的，具有代表性和迁移性．教师不仅要认真教好教材，还要善于挖掘问题的背景和本质，让学生达到“做一题，会一类”，掌握知识的同时，更要培养学生的数学思考能力．在复习过程中，我们要学会整理知识，抽出问题的本质，让学生在思考中提升知识的同时，也提升了学生的数学思考的学习能力．

参考文献

［1］刘绍学．数学必修2．A版［M］．北京:人民教育出版社，2013:124-144．

［2］袁玉芹．“阿波罗尼斯圆”高考现身［J］．数学天地:高中版，2012(2):4-5．

作者简介:叶晓武(1978－)，女，浙江永嘉人，中学数学高级教师，研究方向:数学教育．

修订日期:*收文日期:2015-12-01;2016-01-05．

中图分类号:O123．1

文献标识码:A

文章编号:1003－6407(2016)04-10-04