NA序列部分和之随机和的中心极限定理

邹广玉

(长春工程学院 理学院， 吉林 长春130012)



NA序列部分和之随机和的中心极限定理

邹广玉

(长春工程学院 理学院， 吉林 长春130012)

摘要:部分和之随机和在理论和实际中有着重要价值，中心极限定理则给出了它的渐近分布.利用前人得到的NA序列部分和之和的中心极限定理和部分和最大值的矩不等式,获得了NA序列部分和之随机和的中心极限定理，形成了与独立同分布情形对应的结果，并应用所得结论给出一类随机函数随机和的中心极限定理.

关键词：NA序列；部分和之和；中心极限定理；随机函数

定义 称随机变量{Xi,i∈I}是负相伴(NA)的,如果对于I的任意不交子集A、B,有Cov(g(Xi,i∈A),h(Xj,j∈B))≤0,其中I={1,… ,n}，g与h是任何两个使得协方差存在且对每个变元均非降的函数.

称随机变量序列{Xi,i≥1}是NA的,如果对任何n≥2,X1,…,Xn都是NA的.

NA序列的概念最早由Alam和Saxena[8]提出，它是包含独立随机变量列在内的重要相依类型，在可靠性理论、多元统计分析等有重要应用.

1若干引理

设{Xn,n≥1}为NA随机变量列，记

引理2[6]设{Xn,n≥1}为均值为0的严平稳NA随机变量序列，满足下面条件：

(3) 对某个δ>0,E|X1|2+δ<∞，

则

引理3在引理2的条件下有

2主要结论

定理1设{Xn,n≥1}为满足引理2条件的NA随机变量序列，{τn,n≥1}是取正整数值的随机变量，满足

(1)

其中a是正常数，则有

(2)

(3)

证明：先证式(2).记tn=[an]，注意到

(4)

事实上，由马尔可夫不等式和引理1，有

P{|τn-tn|>tnδ}≤

P{|τn-tn|>tnε}≤

P{|τn-tn|>tnε}≤

P{|τn-tn|>tnε}≤

P{|τn-tn|>tnε}≤

P{|τn-tn|>tnε}.

(5)

式(3)的证明与上面完全类似，从略.

3应用

设Wn=Wn(X1,X2,…,Xn)是一个随机函数(或统计量)，可以表示成

Wn=Sn+Rn,

(6)

其中Rn称为余项.很多常用的随机函数(或统计量)都可表示成式(6)的形式,例如U统计量、Von-Mises统计量、线性模型的误差方差估计量、移动平均过程等.下面讨论这类统计量随机和的渐近分布.

证明:由定理1知

下面说明

(7)

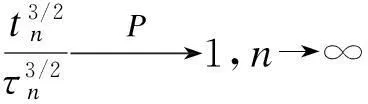
P{τn>2tn}≤

P{τn>2tn}≤

P{o(1)≥ε}+P{τn>2tn}→0,n→∞.

这就证明了式(7)，再由Slutsky定理可知定理2成立.

4结论

中心极限定理一直都是概率极限理论研究的中心问题之一，前人在一定条件下获得了NA序列部分和之和的中心极限定理，本文在同样的条件下将其推广为部分和之随机和的中心极限定理，拓宽了定理的适用范围，并形成了与独立同分布情形对应的结果.作为应用，还得出了一类随机函数随机和的中心极限定理.

参考文献：

[1]RESNICK S I.Limit Laws for Record Values[J].Stochastic Processes and Their Applications，1973，1(1):67-82.

[2]ARNOLD B C，VILLASENOR J A.The Asymptotic Distributions of Sums of Records[J].Extremes，1999，1(3):351-363.

[3]江涛，林日其.I.I.D.随机变量部分和之和的极限定理[J].淮南工业学院学报，2002，22(2):73-75.

[4]江涛，苏淳，唐启鹤.I.I.D.随机变量部分和之随机和的极限定理[J].中国科学技术大学学报，2001，31(4):394-399.

[5]宇世航.同分布NA 序列部分和之和的强大数定律[J].山东大学学报：理学版，2008，43(4):62-66.

[6]宇世航，张锐梅.NA 序列部分和之和的中心极限定理[J].高师理科学刊，2007，27(3):1-4.

[7]兰冲锋，吴群英.随机变量序列部分和之和的完全收敛性[J].统计与决策，2014(1):72-75.

[8]ALAM K,SAXENA K M L.Positive Dependence in Multivariate Distributions[J].Comm.Statist.Theory Math，1981,10(12):1183-1196.

Central Limit Theorem for Random Sum of Partial Sums of NA Sequences

ZOU Guang-yu

(Changchun Institute of Technology, Changchun 130012, China)

Abstract:Random sum of partial sums was of great value in theory and practice ,and its asymptotic distribution was given by the central limit theorem.With the help of the central limit theorem for sum of partial sums and moment inequality for the maximum of partial sum of NA sequences,the central limit theorem for random sum of partial sums of NA sequences was obtained,which corresponded to the result on the I.I.D case.Then by the conclusion given above,a central limit theorem of random sum for a class of random functions was obtained.

Key words:NA sequences;sum of partial sums;central limit theorem;random functions

中图分类号：O211.4

文献标识码：A

doi:10.3969/j.issn.2095-2198.2016.01.017

文章编号：2095-2198(2016)01-0086-04

作者简介：邹广玉(1982-)，男，吉林通化人，博士，讲师，主要从事概率极限理论的研究.

基金项目：国家自然科学基金项目(11401090)；吉林省教育厅重点项目(120120113)；长春工程学院青年基金项目(320130019)

收稿日期：2014-09-03