圆形喷嘴射流特性模拟方法优化选择

王艳芬，　禹言芳，　孟辉波，　王　丰，　吴剑华

(沈阳化工大学 辽宁省高效化工混合技术重点实验室， 辽宁 沈阳 110142)



圆形喷嘴射流特性模拟方法优化选择

王艳芬，禹言芳，孟辉波，王丰，吴剑华

(沈阳化工大学 辽宁省高效化工混合技术重点实验室， 辽宁 沈阳 110142)

摘要:为提高圆形喷嘴射流特性数值模拟研究的准确性、可靠性，分别采用标准k-ε、RNG k-ε、SST k-ω、标准k-ω等4种湍流模型、3种网格划分方案及2种控制方程离散格式对圆形喷嘴射流流场特性进行数值模拟.研究结果表明：与标准k-ε、SST k-ω、标准k-ω三种湍流模型相比，RNG k-ε更能真实地反映圆形喷嘴射流流场特性；在网格划分方案的比较中，方案1所得的平均扭曲率最小，为0.187；对QUICK和二阶迎风格式两种控制方程离散格式的对比发现，二阶迎风格式所得到的轴向速度分布模拟结果更接近实验值.

关键词：圆形喷嘴；射流；数值模拟；湍流模型；网格划分

化学工业是当今世界各国重要的基础工业，它涉及大量的日用化学品和石油化工产品的生产.而化工生产中的混合单元操作设备是化学工业过程中的核心设备，也是能源消耗的主要设备[1-2].在现有的技术中，混合器主要有静态混合器和动态搅拌混合装置两类.静态混合器采用的方法是在管道中置入扰流原件，以改变流动状态使混合物与母液混合；动态搅拌混合装置是利用搅拌器使混合物与母液混合[3].作为动态搅拌混合装置的一种，射流搅拌具有结构简单，制造与安装方便，节能降耗，噪音小等优点.文献[4]曾报道，在化工行业相对发达的美国每年由于混合问题造成的经济损失高达几十亿美元.因此，设计高效的液-液混合设备，并实现液-液的初始快速混合，对于提高产品质量、减少副产物收率、优化整个生产过程具有重要意义[5].

近十几年来，随着现代流场测试技术的不断发展，实验测量工具已经从最初的毕托管、热膜流速仪发展到近期的高精度测量仪器LDV、LIF和PIV.很多研究者采用不同的实验手段对射流进行了研究.张勃等[6]通过热线风速仪对不同宽高比的圆转矩形收敛喷管的射流湍流强度特性进行了试验研究；王长园等[7]在定容装置上利用高速摄影纹影法对不同冲击高度和冲击角度下甲烷高压碰壁射流的扩散和卷吸特性进行了试验研究；Yildiz和Jill[8]采用LDV技术对等温射流和浮射流在不同雷诺数范围内过渡区的流动特性进行了研究；肖洋等[9]利用激光诱导荧光技术对横流中多孔射流的稀释特性进行了实验研究.陈庆光等[10]采用粒子图像测速(PIV)技术对矩形管湍流冲击射流场进行了实验测量，得到了主射流区和冲击区附近测量截面上的平均速度和涡量分布.虽然实验研究能综合考虑影响流动的各种因素，结果客观可靠.但实验测量有投资大、结果的精度和可靠性受测量仪器和环境的影响等问题.而数值模拟分析即计算流体力学(CFD)方法具有投资小和精度易于提高等特点，是一种研究流体流动的有效方法.因此，随着计算机水平和计算技术的不断发展，用数值方法研究流动与传热，已成为当前国际上最活跃的研究领域之一.而且CFD的兴起促进了实验研究和理论分析方法的发展，为简化流动模型提供了更多的依据，使得很多分析方法得到完善和发展，它可以在非常广泛的流动参数范围内，对所有的流场参数进行定量分析，而这往往是采用实验手段和理论分析方法所无法做到的[11].Fluent是一款应用非常广泛的流体流动模拟软件，要实现对一个特定流动过程的精确模拟，必须选用适当的数值方法，这要求从湍流模型、网格划分、控制方程离散格式等方面进行优化选取分析.为了对轴对称射流有一个更完整、全面的理解，本文采用数值模拟的方法对圆形喷嘴射流流场特性进行了数值模拟，同时，对标准k-ε、RNG k-ε、SST k-ω、标准k-ω等4种湍流模型、3种网格划分方案及2种控制方程离散格式进行优化选择，为今后圆形喷嘴射流流场特性的数值研究提供更为可靠的依据.

1物理模型与计算方法

1.1数值模型的建立

余常昭等[12]采用热膜流速仪对圆形断面自由湍动纯水射流的流场进行了实验研究，为保持本文数值模型与该文献中实验模型的一致性，本文数值模拟模型与文献中实验设备尺寸完全相同，数值模型结构与尺寸参数如图1所示.

1 长方体水槽　2 小长方体柱　3 圆形喷嘴　4 流场出口

长方体水槽长×宽×高=2 500 mm×400 mm×600 mm；在距离长方体坐标原点490 mm处建立一个小长方体柱，并将圆形喷嘴建立在小长方体柱表面上，该喷嘴距离底面高度为250 mm，圆形喷嘴直径D=10 mm.

1.2边界条件

模拟介质为水，密度为998.2 kg/m3，黏度1.003×10-3Pa·s.模拟过程中边界设定：喷嘴出口面设为速度入口，速度大小为4.50 m/s，与实验值相同；长方体水槽右端面上部分100 mm高的面设定为自由出口.由于靠近固体壁面区域流体流速较低，处于层流状态，层流底层的黏性作用占优，湍流扩散相对减弱，高雷诺数下的湍流输运方程已不能严格有效，因此在Fluent中，近壁处用标准壁面函数计算.

1.3网格划分

由于数值模型尺寸较大，且本文主要研究射流流动方向的流动特性，故综合考虑网格划分对计算时间和计算精度的影响，采取分区划分网格的方法.对湍流模型的优化选择中，首先对喷嘴前方直径×高=Φ200 mm×500 mm的圆柱体区域进行了网格细化，而其他区域的流场对射流区域流场特性的影响较小，所以其他区域的网格选取了较大的网格尺寸，以节省计算时间，网格划分如图2所示.

图2　网格划分

1.4数值解法

先选取网格划分方案1进行网格划分，对4种不同的湍流模型进行比较；然后选用较好的RNG k-ε湍流模型对3种不同网格划分方案的圆形喷嘴射流流场进行计算，选出较好的网格划分方案.计算过程中，控制方程中离散格式先用二阶迎风格式，设定收敛条件后求解计算，保存计算结果，并在此基础上，改用控制方程中QUICK离散格式，初始化流场，重新求解计算，以对控制方程中这两种离散格式进行对比分析.

2模拟结果对比及分析

2.1不同湍流模型的对比

采用标准k-ε、RNG k-ε、SST k-ω、标准k-ω等4种湍流模型对圆形喷嘴射流特性进行模拟，并将4种不同湍流模型下轴向速度分布与文献[12]中的实验数据进行对比，4种不同湍流模型下轴向速度与实验所测轴向速度值的对比如图3所示，该图所选取截面位置为沿射流轴向截面Z=720 mm处.从图3可以看出:4种湍流模型下的射流轴向速度分布具有一定程度的相似性，均为在射流中心线位置附近轴向速度达到最大，并随径向位置的改变而减小.由图3可直观得出，采用RNG k-ε湍流模拟所得出的轴向速度与实验数值最为接近.由于文献中本次实验测量数据点较少，模拟数据较多，使模拟与实验数据两者之间物理空间位置并不能完全一致，故本文仅对4种不同湍流模型计算结果的轴向分布最大速度与实验所测最大速度值进行对比分析，计算结果发现标准k-ε、RNG k-ε、SST k-ω、标准k-ω与文献中实验数据的误差分别为38.42 %、5.75 %、43.66 %、67.62 %，其中标准k-ε、SST k-ε、标准k-ω湍流模型的计算结果与实验数据相比偏离过大，可不予考虑.通过比较其他不同射流轴向位置处4种不同湍流模型的射流轴向速度分布与实验数据的误差发现，RNG k-ε数值模型的计算结果误差均较小，因此认为RNG k-ε湍流模型能够较好地用于圆形喷嘴射流特性的流场预测.

图3　四种不同数值模型下轴向速度与实验值的对比

2.2网格划分方案对比

生成网格的质量对于CFD模拟结果的准确性和稳定性有很大影响，其中扭曲率是一项重要的表征网格质量好坏的参数，并且小的扭曲率能得到更精确的结果[13].用于圆形喷嘴射流的长方体槽网格的划分可采用不同的区间划分方式，为优化网格的划分方式，本实验共采用了3种较为典型的网格划分方案.方案1:在Z=510 mm处射流喷嘴面正前方建立一个直径为200 mm，高为500 mm的圆柱体，并从Z=510 mm和1 010 mm 处将整个长方体模型分割为3个区域，将整个长方体模型分为4个区域.圆柱体选取六面体结构化网格进行细化，圆柱体外Z=510～1 010 mm区域选取相对较粗的六面体结构网格划分，其他两个区域采用四面体网格划分.该方案网格数目为5 983 799，网格划分如图4(a)所示;方案2:在Z=520 mm处将整个长方体模型分割为2个区域，Z=520 mm后端区域采用六面体结构化网格进行细化，Z=520 mm前端区域采用较粗四面体网格划分，该方案网格数目为4 636 898，网格划分如图4(b)所示;方案3:在Z=510 mm处射流喷嘴面正前方建立一个直径为100 mm，高为400 mm的圆柱体，并从Z=490 mm和1 200 mm处将整个长方体模型分割为3个区域，将整个长方体模型分为4个区域.圆柱体选取较小尺寸四面体网格进行细化，圆柱体外Z=490～1 200 mm区域和Z=490 mm前面区域选取相对较粗的四面体网格划分，Z=1 200 mm后面区域采用更大尺寸四面体网格划分，该方案网格数目为6 147 962，网格划分如图4(c)所示.

各网格划分方案下的网格扭曲率如图5所示.从图5可看出:方案1下的网格扭曲率在0～0.1区间所占百分比取得最大值为66.64 %，并随着网格扭曲率的升高，其所占百分比逐渐降低；方案2下的网格扭曲率亦在0～0.1区间所占百分比取得最大值为51.75 %，但其最大值相比于方案1要小14.89 %；方案3下的网格扭曲率在各区间所占百分随网格扭曲率的增加先增加后减少，并且网格扭曲率所占百分比在区间0.3～0.4取得最大值，其网格扭曲率主要分布在区间0.2～0.5.三种方案下的平均网格扭曲率分别为0.187、0.235、0.360，网格划分方案1所得到的平均扭曲率最小，由此说明其网格质量最佳.因此，选取网格划分方案1为本次数值模拟的网格划分方案可使计算结果更为可靠.

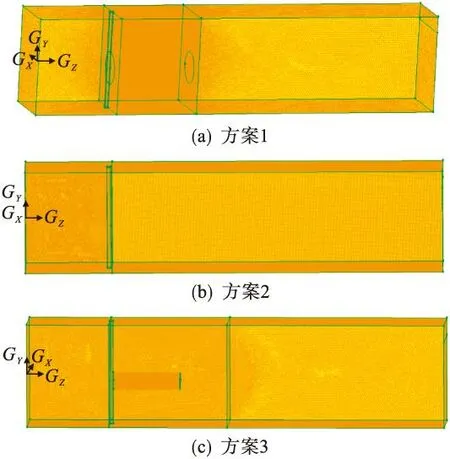
图4　不同网格划分方案

图5　不同网格划分方案的网格扭曲率

2.3离散格式对比

为选择较好的控制方程离散格式对圆形喷嘴射流流场特性进行数值研究，选取前面已验证过的精度较高的RNG k-ε湍流模型，并采用网格方案1进行网格划分，对数值模拟控制方程离散格式中的QUICK格式和二阶迎风格式进行比较分析，并将控制方程离散格式中这两种离散格式计算所得数值模拟结果的射流轴向速度分布与实验所测数据进行对比，依然选取截面位置为沿射流轴向截面Z=720 mm处，所得控制方程离散格式中不同离散格式下轴向速度与实验数据对比如图6所示.从图6可以看出:控制方程离散格式中两种不同离散格式计算所得的轴向速度分布及实验数据均呈现一个纵向波峰分布，并在射流中心线附近位置达到轴向速度分布最大值.从图6还可看出:由二阶迎风格式所得到的轴向速度分布模拟结果比QUICK离散格式更接近实验值，二阶迎风格式和QUICK离散格式所得到的轴向速度分布与实验数据相比，最大轴向速度误差分别为5.75 %和9.04 %.由此得出，二阶迎风格式比QUICK离散格式更能真实地反映圆形喷嘴射流流场.这是因为，尽管控制方程的QUICK离散格式具有近三阶精度，但其一般适用于转动及旋流流场的预测，对于圆形喷嘴水平射流流场，控制方程二阶迎风格式更能真实地反映其流场特性.

图6　不同离散格式下轴向速度与实验值的对比

3结论

为了提高对圆形喷嘴射流流场特性数值模拟研究的准确性，本文采用CFD方法分别从湍流模型选取、网格划分策略、离散格式选取等3个方面对圆形喷嘴射流流场数值模拟方法的选取进行优化，并通过将模拟结果与实验数据对比分析得到了以下结论：

(1) 将标准k-ε、RNG k-ε、SST k-ω、标准k-ω四种湍流模型计算结果与实验数据比较发现，RNG k-ε最接近实验数据，与实验数据相比误差最小，为5.75 %.

(2) 对比3种不同网格划分方案，发现网格划分方案1所得到的平均扭曲率最小，为0.187，由此说明该方案网格质量最佳.

(3) 控制方程中二阶迎风格式和QUICK离散格式所得到的轴向速度分布与实验数据相比，最大误差分别为5.75 %和9.04 %，由此得出，二阶迎风格式所得到的轴向速度分布数值结果比QUICK离散格式更接近实验值.

参考文献：

[1]Jin Y,Cheng Y.Chemical Engineering in China:Past,Present and Future[J].American Institute of Chemical Engineers Journal,2011,57(3):552-560.

[2]Luo P C,Cheng Y,Jin Y,et al.Fast Liquid Mixing by Cross-flow Impingement in Millimeter Channels[J].Chemical Engineering Science,2007,62(22):6178-6190.

[3]王明冲.高效射流混合装置[J].油气田地面工程,2009,28(9):87-88.

[4]Paul E L.Handbook of Industrial Mixing:Science and Practice[M].New York:John Wiley & Sons,2004:5-10.

[5]骆培成,程易,汪展文,等.液-液快速混合设备研究进展[J].化工进展,2005,24(12):1319-1326.

[6]张勃,吉洪湖,曹广州,等.宽高比对矩形喷管射流湍流强度影响试验[J].航空动力学报,2010,25(10):2244-2248.

[7]王长园,刘福水,吴文锋.高压甲烷气体碰壁射流扩散与卷吸特性的试验[J].内燃机学报,2012,30(5):423-428.

[8]Bayazitoglu Y,Peterson J.Modified Similarity Prediction of Jet and Buoyant Jet Entrainment in the Transition Region[J].Experimental Thermal and Fluid Science,1990,3(2):174-183.

[9]肖洋,唐洪武,阿衣丁别克·居马拜.横流中多孔射流的稀释特性实验研究[J].实验流体力学,2011,25(5):35-39.

[10]陈庆光,徐忠,吴玉林,等.矩形管湍流冲击射流场的PIV实验研究[J].实验流体力学,2005,19(1):87-93.

[11]芦绮玲,陈 刚.多孔紊动射流的数值模拟与实验研究进展[J].水科学进展,2008,19(1):137-146.

[12]余常昭,李春华.圆形断面自由湍动射流卷吸的实验研究[J].气动实验与测量控制,1996,10(1):31-38.

[13]Fluent.GAMBIT 2.2 Tutorial Guide[M].Lebanon:Fluent Incorporated,2004:16-18.

Optimization of Numerical Simulation for Characteristic of Circular Nozzle Jet

WANG Yan-fen,YU Yan-fang,MENG Hui-bo,WANG Feng,WU Jian-hua

(Shenyang University of Chemical Technology， Shenyang 110142， China)

Abstract:To improve the accuracy and reliability of the numerical study for circular nozzle jet,four turbulent models,three kinds of mesh generations and two discretization schemes were used to simulate the characteristic of the circular nozzle jet flow field in this paper.The result showed that RNG k-ε model could reflect the real circular nozzle jet flow field more accurately than another three turbulent models.It turned out that the average skewness of the first meshing scheme was the minimum.At last,taking the two discretization schemes into consideration,it was found that second order upwind got a closer result to the experimental value than QUICK discretization scheme.

Key words:circular nozzle;jet;numerical simulation;turbulence model;mesh generation

中图分类号：TQ051.7

文献标识码：A

doi:10.3969/j.issn.2095-2198.2016.01.011

文章编号：2095-2198(2016)01-0055-05

作者简介：王艳芬(1988-)，女，河南安阳人，硕士研究生在读，国家奖学金获得者，主要从事高效化工设备的研究.通讯联系人：吴剑华(1951-)，男，辽宁沈阳人，教授，硕士，主要从事化工过程强化的研究.

基金项目：国家自然科学基金(21106086,21306115，21476142);辽宁省博士科研启动基金(20131090);辽宁省高等学校优秀人才支持计划(LR2015051)

收稿日期：2013-12-20