10 kV三芯电缆应急时间计算模型与验证*

刘刚　王鹏　李文祥

(1.华南理工大学 电力学院， 广东 广州 510640； 2.广州供电局有限公司， 广东 广州 510620)



10 kV三芯电缆应急时间计算模型与验证*

刘刚1王鹏1李文祥2

(1.华南理工大学 电力学院， 广东 广州 510640； 2.广州供电局有限公司， 广东 广州 510620)

摘要：以单根直埋敷设的10 kV三芯电缆为研究对象，建立了电缆暂态热路模型，并将其简化等效为一阶RC热路，根据所建立模型推导了应急时间与线芯温度的关系式。同时，设计了直埋敷设电缆加载不同应急负荷时的温升实验，实测了各组实验的应急时间。通过与应急时间计算值的对比，分析实验结果与误差，验证了理论计算的正确性，并得到不同应急负荷下的电缆应急时间变化规律，为电力部门指导电力电缆的运行提供理论支持.关键词： 三芯电缆；直埋敷设；暂态热路模型；线芯温度；应急时间；应急负荷

随着经济的高速发展，我国城市的用电需求量越来越大，城市配网电缆也得到了大规模的应用.然而，由于城市可用土地紧缺、建设资金限制以及配网电缆敷设错综复杂等因素，导致不能在某些城市的中心地段建设新的电缆线路，因此一些配网电缆线路会出现短时过负荷的情况.同时，当线路发生故障或检修时，运行中配网三芯电缆能否作为备用线路接受短时过载以及允许过载的时间有多长，同样是一个急需解决的问题[1].

较主网的单芯电缆而言，配网10 kV三芯电缆有如下几个特点：(1)三芯电缆在结构上3个导体的分布并不是相互接触，三相线芯由绝缘层分相包围，在电缆散热过程，其3个线芯作为热源，成“品”字形分布，并不是在电缆的几何中心；(2)配网10 kV三芯电缆的敷设方式多为多排管敷设或电缆沟敷设，敷设形式日益多样，非传统的敷设方式也开始大量使用[2]；(3)配网10 kV三芯电缆负荷类型多样，不同时刻不同电缆的负荷特性都不一样，持续时间下同时达到额定负荷运行的情况几乎不会出现.目前，国际公认的配网电缆载流量的计算标准是IEC60287中的稳态三芯电缆载流量公式，而IEC标准里的载流量算法是基于热路法得出的.IEC标准由于只适用于工程设计的参考，没有对三芯电缆的暂态热路模型进行研究，也没有对误差的产生展开分析.另外，在短时提高配网10 kV三芯电缆载流量的过程中，电缆热时间常数是一个重要指标，它表征电缆导体温度变化的快慢程度，计算配网10 kV三芯电缆的暂态温升时间，可以为城市供电系统中的负荷调度和配网电缆输送容量的短时提高提供重要参考，目前国内外对于这方面开展的研究相对较少[3- 5].

为了对电缆应急时间进行系统研究，文中根据三芯电缆的物理结构、电缆的传热机理以及电缆实际负载情况，建立了电缆暂态传热模型，根据模型推导出10 kV三芯电缆应急时间计算公式，利用公式以及电缆结构和负荷参数计算不同过负荷下的应急时间.同时，设计直埋敷设下的暂态阶跃电流温升实验，通过对不同接入负荷电缆的实验研究与分析，得到实验条件下的电缆暂态应急时间，然后对比理论值与计算值，得出能够指导实际应用的应急时间结果.

110 kV三芯电缆应急时间计算必要性分析

电力系统配电网络与用户直接相连，其接线方式取决于用户负荷的性质，对于第一级及第二级负荷占比较大的用户，一般应采用可靠性较高的有备用接线，即当任一段线路发生故障或检修时，该线路的负荷由备用线路应急供电.另外，由于配网电缆的实际运行负荷情况复杂多变，每天不同时间段的负荷情况不同，并且负荷波动性很大，存在负荷突变情况，甚至在某一时段电缆载流量会超过额定负荷.但是，电缆运行中的10 kV三芯配网电缆由于具有较大的热时间常数，当负荷突然变化时，其导体温度不能发生突变，一定程度的短时过负荷运行不一定会使得导体温度超过90 ℃(绝缘材料XLPE的长期耐受温度).对于当线路发生故障检修或者负荷变动较大时，运行中配网三芯电缆能否作为备用线路接受短时过载、允许过载的时间有多长等问题，目前鲜有文献对此进行分析.允许过载的时间称为应急时间，因此，应急时间的计算成为了电力部门急需解决的问题[6- 7].

由于10 kV三芯电缆的负荷特性与其应急时间息息相关，选取某市代表性的配网10 kV三芯电缆(具体型号为YJV22-3×240 mm2)，图1所示为该线路5月内负荷情况较为严重的6天的运行数据.

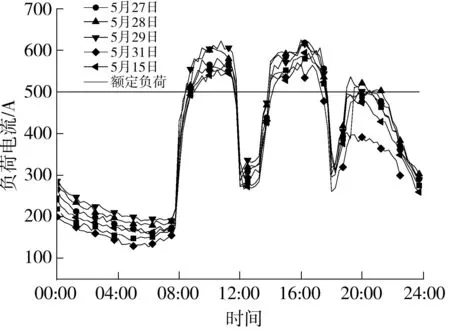
图1　某市5月内6天超负荷运行数据

从图中可以看出，该电缆的日负荷曲线波动性明显，在一天的高负荷时段内，一定时间电缆的负荷电流会超过额定负荷，甚至达到120%额定负荷.而在其他时段电缆负载可低至20%额定负荷，利用率仅为电缆额定容量的1/5.由此可见，配网10 kV三芯电缆在日常运行中的负荷波动性很大，存在电缆负荷突变情况，且在某一时段，负荷电流会超过电缆的额定容量.

目前国内外由于技术限制，很难实现对运行中电缆导体温度的直接精确测量.同时又由于IEC 60287标准以及众多算法的局限性，使得迄今为止仍难以准确得到电缆运行时的实际线芯温度，因此无法通过对应急状况下电缆导体温度的实时监控而得到应急时间值.目前对于应急时间的计算主要通过建立电缆的热路模型从而求得热时间常数，采用热时间常数来表征电缆导体温度变化的快慢程度，最终求得应急负荷时电缆的应急时间.然而，国内外对电缆应急时间的研究仍十分有限，而且大都通过试验对温度曲线拟合求得热时间常数[8]，进而求得应急时间.对于配网10 kV三芯电缆而言，由于其敷设环境多变，所在位置的环境热阻、环境温度、湿度、风速、太阳辐射等因素都将影响电缆的发热，因此配网三芯电缆的发热情况受实时性因素影响很大，在这些条件下由曲线拟合求得的应急时间计算值误差很大，故此时由曲线拟合求应急时间的方法不具科学性.另外，目前对应急时间的研究大多数集中在高压单芯上，真正针对10 kV三芯电缆结构特点以及传热特点而提出应急时间的计算仍未见报道[9- 10].

建立电缆暂态热路模型可以实现由电缆表面温度实时计算导体温度，将其等效为一阶RC暂态热路后，类比电路的暂态理论，也可应用于求解暂态的温升时间.利用所建立的10 kV三芯电缆暂态热路模型，研究在一定初始负荷下，电缆突然加载应急负荷到导体达到长期允许耐受温度(90 ℃)时的应急时间，可为指导电力负荷调度和控制电缆检修工作的时间提供重要参考.

210 kV三芯电缆暂态热路模型

电缆稳态运行时，电缆导体的发热温升不随时间变化；电缆暂态运行时，导体的温升则是时间的函数.因此，为了研究10 kV三芯电缆不同负荷情况下的应急时间，要对电缆的暂态运行过程进行分析，就要构建合适的10 kV三芯电缆暂态热路模型.

针对单根直埋敷设的10 kV三芯电缆，计算线芯温度与应急时间只需要考虑电缆表皮温度，因此，对于电缆周围敷设环境来说，假设其外部环境基本不变，即环境温度恒定，这对电缆建模以及之后的暂态计算不产生影响.

根据10 kV三芯电缆内部结构与热场仿真结果，建立其稳态热路模型[11- 13]，如图2所示.

图2　10 kV三芯电缆稳态热路模型

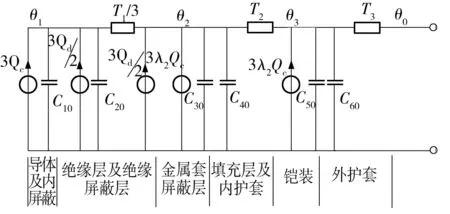
图3　10 kV三芯电缆暂态热路模型

Fig.3Transient thermal circuit model of 10 kV three-core cable

根据IEC标准[14]，计算图3中各参数值，如下所示.

绝缘层的热阻T1：

(1)

式中：ρT1为绝缘层的热阻系数，取3.5(K·m)/W；G为几何因素，K为屏蔽因素，均参考IEC标准中的图解法得出，分别取0.78和0.997.

填充层及内护套的热阻T2：

(2)

式中：ρT2为内护套的热阻系数，取6.0(K·m)/W；G0为几何因素，取0.49.

外护套的热阻T3：

(3)

式中：ρT3为外护套的热阻系数，取6.0(K·m)/W；d为外护套的厚度，mm；D为铠装层的外径，mm.

由式(1)-(3)可得出IEC标准法计算10 kV三芯电缆各层结构的热阻值为：T1=0.437(K·m)/W，T2=0.464(K·m)/W，T3=0.09(K·m)/W.

各层热容C的计算：

由热容的定义可知，导热材料的热容等于其比热容乘以质量，而质量又只与密度和体积有关.对于单位长度的10 kV三芯电缆的各层结构的热容，计算公式如下：

C=cρV,

式中：c为材料的比热容，J/(kg·K)；ρ为密度，kg/m3；V为材料的单位长度体积，m3.

利用热路模型中的串并联关系简化图3，可得图4.

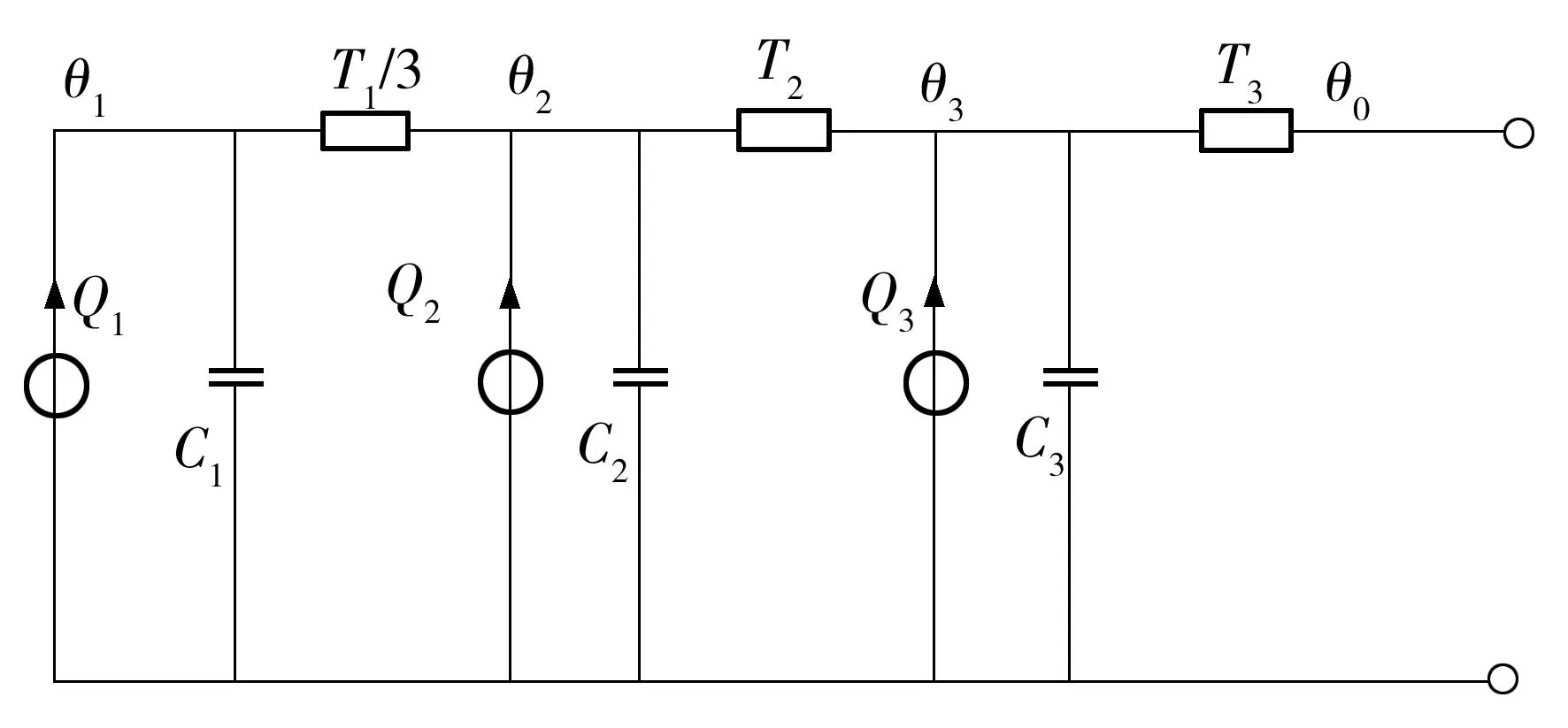
图4　10 kV三芯电缆暂态热路简化模型

Fig.4Simplified model of transient thermal circuit of 10 kV three-core cable

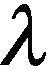
通过利用图4中3种损耗的损耗比例消去Q2和Q3，使之简化成为只有单一热流源Q1的热路模型；然后将各个热阻热容等效为集中参数，使之简化为一阶TC等值热路[15]，等效模型如图5所示.

Q2与Q1之间的损耗比为

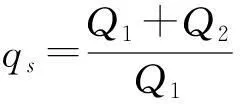
Q2、Q3与Q1之间的损耗比为

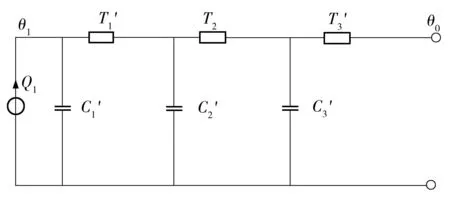
图5　暂态等效模型

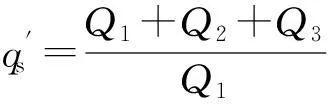
310kV三芯电缆暂态应急时间计算模型

电缆载流量的阶跃变化引起的导体暂态温度响应取决于电缆内部各部分的热阻和热容，为了计算三芯电缆导体暂态温升时间，就需要对上述电缆暂态热路模型做进一步的等效，根据文献[15- 18]可将上述模型等效为只有热阻与热容的一阶TC等效热路.直埋敷设下的10 kV三芯电缆一阶TC等效电路如图6所示.

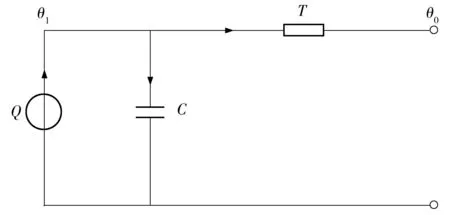
图6　直埋敷设下的10 kV三芯电缆一阶TC等效电路

Fig.6Order TC equivalent circuit of 10 kV three-core cable under laying soil

将图5中的热阻与热容变为集中参数[14,19]，可得T、C的表达式：

(4)

(5)

根据图6所示的直埋敷设下10kV三芯电缆一阶TC等效电路，利用传热学原理建立热平衡方程[17]：

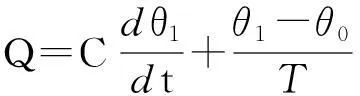
求得方程通解为

θ1=QT+θ0+Ae-t/TC.

设施加应急负荷前电缆导体稳态温度为θ10，当初始条件为t=0时，由上述方程可得

A=θ10-θ0-QT.

故方程通解为

θ1=(θ10-θ0-QT)e-t/TC+QT+θ0

(6)

则应急时间t为

t=TC[ln(θ10-θ0-QT)-ln(θ1-θ0-QT)]

(7)

将方程的通解(7)写成关于时间的函数，得到不同时刻下应急时间的表达式：

(8)

4实验分析与验证

为了验证所建立的10 kV三芯电缆暂态应急时间计算模型对于计算电缆应急时间的准确性与可靠性，设计了电缆升流试验系统，通过加载不同应急负荷，并对不同实验组的电缆线芯温度进行测量，将实验值与理论计算值进行了对比.

4.1实验装置与实验方法

实验系统可分为两个部分，即为室内部分和室外部分.室内部分主要由调压器、升流器和实验电源组成，室外部分由实验电缆(型号YJV22-3×240 mm2，额定载流量为Imax=530 A)、自动测温仪组成，整个系统的电气接线如图7(a)所示.

对于三芯电缆来说，为了保证其内部每根线芯通过的电流相等，把三相线芯首尾相接，最终把A相和C相线芯的一端接至升流器的二次侧，具体接线如图7(b)所示，如此则可保证实验电缆横截面温度场的对称性.

为了得到三芯电缆加载应急负荷时的应急时间，

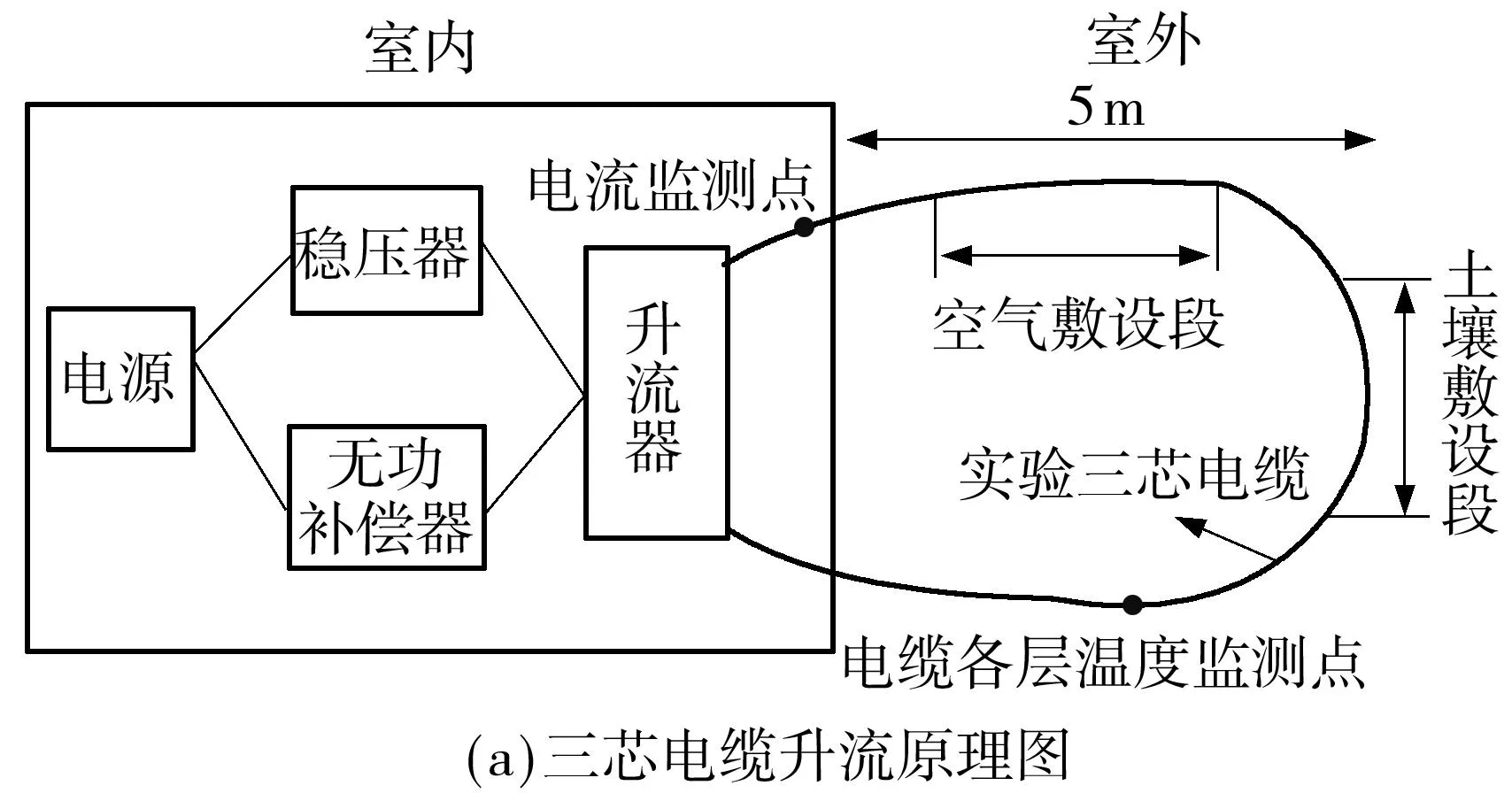
图7　10 kV三芯电缆试验原理图

本实验设计6组加载电流实验.第一组实验初始负荷为50%Imax(其中Imax为额定负荷)，应急负荷为120%Imax；第二组实验初始负荷为50%Imax，应急负荷为150%Imax；第三组实验初始负荷为50%Imax，应急负荷为200%Imax；第四组实验初始负荷为Imax，应急负荷为120%Imax；第五组实验初始负荷为Imax，应急负荷为150%Imax，第六组实验初始负荷为Imax，应急负荷为200%Imax.具体加载电流情况如表1所示.每组实验过程为三芯电缆加载初始负荷达到热平衡稳态后，突然加载应急负荷，当电缆线芯温度达到90 ℃时终止实验.由测温仪所记录的实验数据，得到直埋敷设条件下10 kV三芯电缆加载应急负荷时的电缆线芯温度变化曲线，该实验电缆埋深1 m.

表1各组实验的电流加载情况

Table 1Current loading conditions of the experiment in each group

实验序号初始负荷/A应急负荷/A12656362265795326510604530636553079565301060

4.2实验数据处理与结果分析

针对上述各组实验电流加载情况，分两种情况(即初始负荷为任意负荷的超负荷运行状态和初始负荷为额定负荷的超负荷运行状态)分析电缆线芯温度与应急时间的变化趋势.另外，在6组实验过程中，由于电缆周围直埋环境情况的变化(例如环境温度随时间的变化、直埋水分迁移等因素[23])，加载初始负荷达到稳态时的线芯温度会存在偏差，允许存在1 ℃的误差.

4.2.1电缆初始负荷为任意负荷的超负荷运行状态

根据电缆实际运行负荷情况，任意选择一组运行负荷作为实验研究对象，此时，选择50%Imax，即265A作为实验电缆的初始负荷.

图8为10 kV三芯电缆加载初始电流265 A突变到3种不同超负荷时的电缆线芯温度变化趋势图.

图8加载初始电流由265 A突变为3种不同超负荷时的线芯温度变化曲线

Fig.8Changing curves of cable core conduct temperature when load current mutates from 265 A to three different overload currents

从图8中可以得到，加载电流由50%Imax突变到120%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载50%Imax达到热平衡稳态时，电缆线芯工作温度为49.2 ℃.加载应急负荷636 A后，电缆线芯温度由49.2 ℃上升到90 ℃所用的时间为101 min.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由50%Imax变为120%Imax时，电缆线芯温度在101 min后达到额定工作温度，即应急时间为101 min.

加载电流由50%Imax突变到150%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载50%Imax达到热平衡稳态时，电缆线芯工作温度为50.1 ℃.加载应急负荷795 A后，电缆线芯温度由50.1 ℃上升到90 ℃所用的时间为51 min.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由50%Imax变为150%Imax时，电缆线芯温度在51 min后达到额定工作温度，即应急时间为51 min.

加载电流由50%Imax突变到200%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载50%Imax达到热平衡稳态时，电缆线芯工作温度为49.6 ℃.加载应急负荷1 060 A后，电缆线芯温度由49.6 ℃上升到90 ℃所用的时间为29 min.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由50%Imax变为200%Imax时，电缆线芯温度在29 min后达到额定工作温度，应急时间为29 min.

4.2.2电缆初始负荷为额定负荷的超负荷运行状态

图9为10 kV三芯电缆加载电流由额定负荷530 A突变到3种不同超负荷的过程中，电缆线芯温度的变化趋势图.

图9加载电流由额定负荷530 A突变为3种不同超负荷时的线芯温度变化曲线

Fig.9Changing curves of cable core conduct temperature when load current mutates from rated 530 A to three different overload current

从图9中可以得到，加载电流由额定负荷Imax突变到120%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载额定负荷Imax达到热平衡稳态时，电缆线芯工作温度为83.5 ℃.加载应急负荷636 A后，电缆线芯温度由83.5 ℃上升到90 ℃所用的时间为680 s.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由额定负荷变为120%Imax时，电缆线芯温度在680 s后达到额定工作温度，即应急时间为11.3 min.

加载电流由额定负荷Imax突变到150%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载额定负荷Imax达到热平衡稳态时，电缆线芯工作温度为83.9 ℃.加载应急负荷795 A后，电缆线芯温度由83.9 ℃上升到90 ℃所用的时间为400 s.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由额定负荷变为150%Imax时，电缆线芯温度在400 s后达到额定工作温度，即应急时间为6.7 min.

加载电流由额定负荷Imax突变到200%Imax的过程中，三芯电缆在未达到热平衡稳态时，电缆线芯温度已经达到额定工作温度90 ℃.三芯电缆加载额定负荷Imax达到热平衡稳态时，电缆线芯工作温度为84.5 ℃.加载应急负荷1 060 A后，电缆线芯温度由84.5 ℃上升到90 ℃所用的时间为120 s.因此，对于直埋敷设的10 kV三芯电缆，当负荷电流由额定负荷变为200%Imax时，电缆线芯温度在120 s后达到额定工作温度，应急时间为2 min.

4.3应急时间理论计算与实验结果对比

根据式(4)、(5)可以得到，直埋电缆等效热路模型的热阻T=0.719 7(K·m)/W，集中热容C=4 136.8 J/K.

根据式(10)，并利用Matlab数学软件编程求解方程.理论计算与实验结果对比如表2所示.

表2不同超负荷电流下的电缆应急时间计算值与实验值

Table 2Calculated and experimental current values of cable emergency time under different over loads

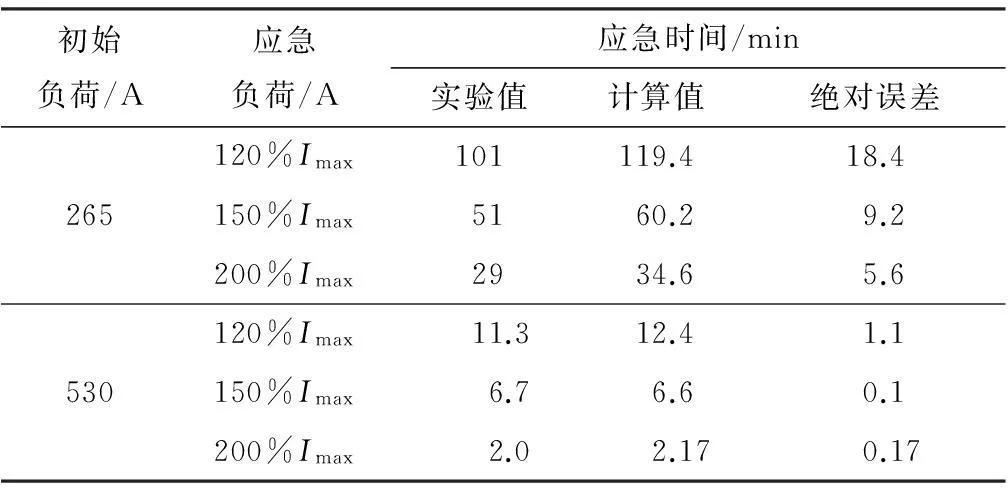
初始负荷/A应急负荷/A应急时间/min实验值计算值绝对误差120%Imax101119.418.4265150%Imax5160.29.2200%Imax2934.65.6120%Imax11.312.41.1530150%Imax6.76.60.1200%Imax2.02.170.17

从表2中可以看出，直埋敷设下的10 kV三芯电缆，随着加载应急负荷的增大，即电缆承受的超载程度越大，不管是应急时间计算值还是实验值都越来越小.并且，根据6组实验的计算值与实验值的绝对误差可知，随着应急负荷的增大，电缆应急时间计算值与实验值之间的误差也越来越小.

总之，利用建立的直埋敷设下10 kV三芯电缆暂态热路模型来对电缆应急时间进行理论计算，根据上述的实验结果，在任意初始负荷下加载应急负荷，其电缆应急时间都是随加载应急负荷增大而减小.根据实验数据的分析可知，应急时间的计算值与实验值之间的误差在合理范围内，验证了推导的应急时间计算公式的可靠性，并且误差的变化符合“越急越准”的特性，即应急时间越短，误差越小.这种电缆应急时间的变化特性有利于对电力运行部门的工作进行指导.

5结论

为了保证10 kV配网三芯电缆发生故障或检修后备用线路在接受短时过载负荷时的安全稳定运行，建立了直埋敷设下的三芯电缆应急时间计算模型，设计了电缆暂态应急实验，通过对比分析应急时间理论计算值与实验值，得到如下结论：

(1)对于直埋敷设的10 kV三芯电缆，当负荷电流由50%额定负荷变为3种不同的应急负荷时，即应急负荷从120%Imax到200%Imax，应急时间计算值从119.4 min减小到34.6 min，实验值从101 min减小到29 min.并且，电缆应急时间计算值与实验值之间的误差也越来越小，从18.4 min减小到5.6 min.

(2)对于直埋敷设的10 kV三芯电缆，当负荷电流由额定负荷变为3种不同的应急负荷时，即应急负荷从120%Imax到200%Imax，应急时间计算值从12.4 min减小到2.17 min，实验值从11.3 min减小到2 min.并且，电缆应急时间计算值与实验值之间的误差也越来越小，从1.1 min减小到0.17 min.

(3)直埋敷设下10 kV三芯电缆应急时间的计算值与实验值之间的误差在合理范围内，实验证明所推导的应急时间计算公式是可靠的，并且误差的变化符合“越急越准”的特性，即应急时间越短，误差越小.

参考文献：

[1]何仰赞，温增银．电力系统分析(上册) [M] ．武汉：华中科技大学出版社，2009.

[2]汤毅，王晓并，陈燕萍，等．10 kV三芯交联电缆载流量的试验研究 [J]．高电压技术，2009，35(11)：2807- 2812．

TANG Yi，WANG Xiao-bing，CHEN Yan-ping，et al.Experimental research on the current rating of 10 kV three-core XLPE cables [J].High Voltage Engineering，2009，35(11):2807- 2812．

[3]MICHAEL R Y，Peter G K.Thermal characteristics of energized shielded drag and an unshielded reeled trailing cable [J].IEEE Transactions on Industry Applications,1991,27(4):791- 796.

[4]IWA Garniwal,AHMAD Burhani.Thermal incremental and time constant analysis on 20 kV XLPE cable with current vary [C]∥Proceedings of 8th International Conference on Properties and Applications of Dielectric Materials.Bali:IEEE,2006.

[5]KATSUICHI Ohata,SHINJI Sakurai,NAOTAKA Ichiyanagi,et al.Transient temperature rise of tunnel for po-wer cables [J].IEEE Transactions on Power Delivery,1990,5(2):745- 752.

[6]ZHOU Xin,NIU Hai-qing．Transient modeling of calculation temperatures of single-core cables [C]∥Proceedings of Power and Energy Engineering Conference.Wuhan:[s.n.],2009:1- 4.

[7]KIRAR M K,AGINHOTRI G.Cable sizing and effects of cable length on dynamic performance of induction motor [J].Power India Conference,2012,30(2):1- 6.[8]NASKAR A K,BHATTACHARYA N K,SAHA S,et al.Thermal analysis of underground power cables using two dimensional finite element method [C]∥IEEE International Conference on Condition Assessment Techniques in Electrical Systems.Kolkata:[s.n.],2013:94- 99.

[9]Naskar A K Bhattacharya N K Saha S,et al.Transient temperature analysis and short-term ampacity calculation of power cables in tunnel using SUPG finite element method [C]∥Industry Applications Society Annual Meeting,2013 IEEE.Lake Buena Vista:[s.n.],2013:1- 4.

[10]LU Xu,ZHAO Ai-xuan．Calculation of distribution cable steady and transient temperature field in ducts [C]∥International Conference on Electricity Distribution.Shenzhen:[s.n.],2014:1280- 1283.

[11]杨强胜，浦保荣．高等传热学 [M].上海：上海交通大学出版社，2001.

[12]杨世铭，陶文铨．传热学 [M].北京：高等教育出版社，2003.

[13]闫澜锋．10 kV三芯电缆温度场分布特性及导体温度计算的仿真与实验研究 [D]．广州：华南理工大学电力学院，2012.

[14]IEC 60853,Calculation of the cyclic and emergency current rating of cables [S].

[15]张尧，周鑫，牛海清,等．单芯电缆热时间常数的理论计算与试验研究 [J]．高电压技术，2009，35(11)：2801- 2806.

ZHANG Yao，ZHOU Xin，NIU Hai-qing，et al．Theoretical calculation and experimental research on thermal time constant of single-core cable [J]．High Voltage Engineering，2009，35(11)：2801- 2806．

[16]刘刚，周凡，黄旭锐,等．环境温度和环境热阻对单芯电缆导体温度计算灵敏度的影响分析 [J]．广东电力，2012，25(10)：51- 54．

LIU Gang，ZHOU Fan，HUANG Xu-rui，et al．The influence of ambient temperature and thermal resistance on the temperature sensitivity of single conductor cable conductor [J]．Guangdong Electric Power，2012，25(10)：51- 54．

[17]刘刚，雷成华．提高单芯电缆短时负荷载流量的试验分析 [J]．高电压技术，2011，37(5)：1288- 1292．

LIU Gang，LEI Cheng-hua.Experimental analysis on increasing temporary ampacity of single-core cable [J].High Voltage Engineering，2011，37(5)：1288- 1293．

[18]郑肇骥，王琨明．高压电缆线路 [M]．北京：水利电力出版社，1983．

[19]马国栋．电线电缆载流量 [M]．北京：中国电力出版社，2003．

[20]刘毅刚,罗俊华.电缆导体温度实时计算的数学方法 [J] .高电压技术，2005,31(5)：52- 54.

LIU Yi-gang，LUO Jun-hua.Mathematical method of temperature calculation of power cable conductor in real time [J]．High Voltage Engineering，2005，31(5)：52- 54．

[21]宋长华．热路图分析法在传热学课程中的应用 [J]．重庆电力高等专科学校学报，2004，9(3)：19- 24.

SONG Chang-hua．Use of heat circuit diagram methods in the course of heat transfer [J].Journal of Chongqing Electric Power College,2004,9(3):19- 24.

[22]雷科夫.热传导理论 [M]．裘裂钧，丁履,译．北京：高等教育出版社，1955.

[23]CAI Yue,LIU Gang,LEI Cheng-hua．Research on the correlation between cable coretemperature and laying environment [C]∥2010 3rd International Conference on Power Electronics and Intelligent Transportation System.Shenzhen:[s.n.],2010：433- 436.

Calculation Model and its Verification for Cable Emergency Time of 10 kV Three-Core Cable

LIUGang1WANGPeng1LIWen-xiang2

(1.School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Guangzhou Power Supply Bureau Co.,Ltd.,Guangzhou 510620,Guangdong,China)

Abstract:A transient thermal circuit model of 10 kV three-core cables directly laid in soil is established and simplified into an equivalent first-order RC thermal circuit. Then,the relationship between the emergency time and the core temperature is deduced by using the established model,and the temperature rising experiments of the cable are designed and carried out to measure the emergency time under different emergency loads.Finally,the measured values are compared with the calculated ones to verify the correctness of the theoretical calculation,discover the causes of error and reveal the variation of cable’s emergency time under different emergency loads. The present study provides a theoretical foundation for the operation of power cables in power sectors.

Key words:three-core cable;direct burial laying;transient thermal circuit model;core temperature;emergency time;emergency load

doi：10.3969/j.issn.1000-565X.2016.02.013

中图分类号：TM 726.4

文章编号：1000- 565X(2016)02- 0081- 08

作者简介：刘刚(1969-)，男，副教授，主要从事智能高压电网、过电压及其防护、电力设备外缘等的研究.E-mail：liugang@scut.edu.cn

*基金项目：国家高技术研究发展计划(863计划)项目(2015AA050201)

收稿日期：2015- 01- 07

Foundation item: Supported by the National High-Tech R & D Program of China(863 Program)(2015AA050201)