部分柱顶滑移钢筋混凝土结构的滑移柱P-δ效应*

吴波　吕文龙,2

(1.华南理工大学 亚热带建筑科学国家重点实验室， 广东 广州 510640；

2.广东省建筑科学研究院集团股份有限公司， 广东 广州 510500)



部分柱顶滑移钢筋混凝土结构的滑移柱P-δ效应*

吴波1吕文龙1,2

(1.华南理工大学 亚热带建筑科学国家重点实验室， 广东 广州 510640；

2.广东省建筑科学研究院集团股份有限公司， 广东 广州 510500)

摘要：为揭示部分柱顶滑移钢筋混凝土结构中滑移柱的P-δ效应，首先对该类柱的上端铰接简化模型的有效性进行了验证，在此基础上考察了不同情况下无侧移滑移柱因P-δ效应引发的二阶弯矩的特点，指出了需考虑二阶弯矩的界限条件，并就此提出了无侧移滑移柱弯矩增大系数的确定方法，然后通过参数修正初步考虑了混凝土非线性对前述结果的影响，最后给出了算例分析.研究表明：小震阶段采用普通铰对滑移柱顶部的摩擦支座进行近似处理是可行的；在某些情况下，无侧移滑移柱因P-δ效应引发的二阶弯矩对柱身最大弯矩有增大效应，此时只需利用无侧移滑移柱的一阶弯矩和弯矩增大系数，即可方便地确定其考虑P-δ效应后的柱身最大弯矩.

关键词：钢筋混凝土结构；柱顶滑移；P-δ效应；弯矩；增大系数

历次震害表明，建筑物强震倒塌是造成人员伤亡和经济损失的主要原因.文献[1]开展了3个单层框架-剪力墙模型结构的落层倒塌碰撞试验，考察了模型结构的落层倒塌模式和相应的碰撞荷载时程及其平面分布，研究表明剪力墙面外折断和柱轴压比增大是诱发落层倒塌的重要原因.文献[2]研究了板柱结构倒塌与内部柱和周边柱受力的关系，给出了4种倒塌防范措施.文献[3]在楼面梁的位置预先设置钢缆，框架柱失效后荷载通过钢缆传递，试验表明这种措施可以防止结构连续倒塌.文献[4]提出了抗倒塌部分柱顶滑移框架结构的基本思想.文献[5]将该思想拓展到超高层建筑的常用结构形式——框剪结构，介绍了部分柱顶滑移框剪结构的设想，对比了该新型结构与传统框剪结构的设计过程，并初步比较了二者的经济性及弹塑性地震响应，给出了滑移柱柱顶摩擦系数的估算方法.文献[6]对部分柱顶滑移框剪结构进行了深化研究，以进一步改善其经济性，同时提高滑移柱柱顶摩擦系数估算的简便性.文献[7]开展了部分柱顶滑移框剪结构模型的地震模拟振动台试验，研究表明该新型结构的抗震性能优于传统框剪结构.

在钢筋混凝土结构中，因绝大部分偏心压杆长细比偏小，在受力中不存在失稳的危险，故不需作稳定验算，但仍需考虑竖向力在产生了侧移的结构中以及轴向力在产生了挠曲的杆件中引起的附加内力和附加变形，即考虑二阶效应.在二阶效应分析中，通常称轴压力在产生了挠曲的杆件中引起的附加挠度和附加内力为P-δ效应(也称杆件挠曲引发的二阶效应)[8].一般情况下，部分柱顶滑移结构中滑移柱的长细比较小，P-δ效应对其内力及侧向变形影响有限.但某些特殊情况下(如挑空层、局部大空间层等)滑移柱仍可能具有较大长细比，故给出其P-δ效应的计算方法是必要的.虽然文献[8- 13]分别提出了常规柱的挠曲二阶效应处理方法，但无法直接适用于滑移柱.为此，文中对滑移柱的挠曲二阶效应进行了探讨，给出了其P-δ效应计算方法.

1部分柱顶滑移钢筋混凝土框剪结构简述

部分柱顶滑移框剪结构的某些框架柱在其柱顶部位与相邻节点断开，并在二者之间设置摩擦支座.当摩擦支座的摩擦系数较小时，这部分框架柱(即滑移柱)将主要承受上部结构传来的轴力而较少承受弯矩和剪力，强震作用下它们可基本保持完好.若它们在设计之初就被赋予单独承担绝大部分结构自重的能力，则可较好地确保结构的抗倒塌能力.

1.1滑移柱柱顶与相邻节点的连接及其力学模型

滑移柱柱顶与相邻节点之间的摩擦支座由上摩擦板和下摩擦板组成(图1(a)).小震作用下，为充分利用滑移柱的抗侧刚度，一般希望摩擦支座不起滑，此时该支座可传递剪力和少量弯矩.作为近似处理，对于小震阶段的摩擦支座，文中采用普通铰进行模拟，即滑移柱的上、下边界条件分别为铰接和刚接(图1(b)).

大震作用下摩擦支座已经起滑，故采用图1(c)所示摩擦单元进行模拟.每个摩擦单元由两个节点组成:节点1位于下摩擦板中心位置，与柱单元共用节点；节点2位于节点核心区中心位置，与梁单元共用节点.摩擦单元也可用于小震计算，但计算过程相比普通铰繁琐.

1.2普通铰模型的验证

考虑图2所示三层平面框剪结构，混凝土强度等级C30，框架梁截面250 mm×700 mm，滑移柱与非滑移柱截面均为400 mm×400 mm，剪力墙截面200 mm×1 200 mm.框架梁均布荷载50 kN/m，1- 3层作用的水平集中荷载分别为20、40和60 kN.为保证摩擦支座不起滑，各层摩擦系数均取为0.1.摩擦支座近似采用普通铰进行模拟时的结构称为模型A，摩擦支座采用摩擦单元进行模拟时的结构称为模型B.图3所示为两模型计算结果的对比，计算采用通用软件SAP2000进行.从图中可以看出:(1)两模型的计算结果非常接近，这表明小震阶段采用普通铰对滑移柱顶部的摩擦支座进行近似处理是可行的；(2)滑移柱上、下两端之间的水平相对变形非常有限，为此下面近似针对无侧移滑移柱进行P-δ效应的探讨.

图1　滑移柱柱顶与相邻节点的连接及其力学模型

Fig.1Joints and mechanical models of connection between sliding column’s upper end and adjacent joint

图2　三层平面框剪结构

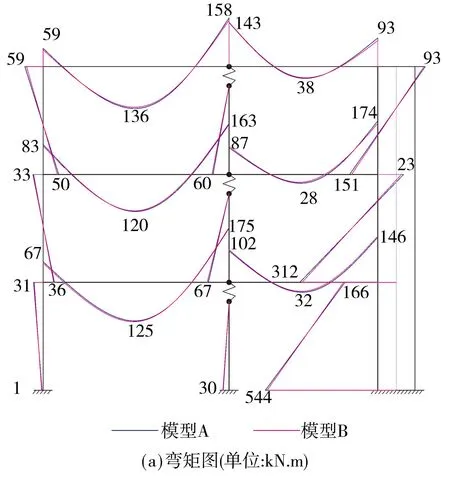
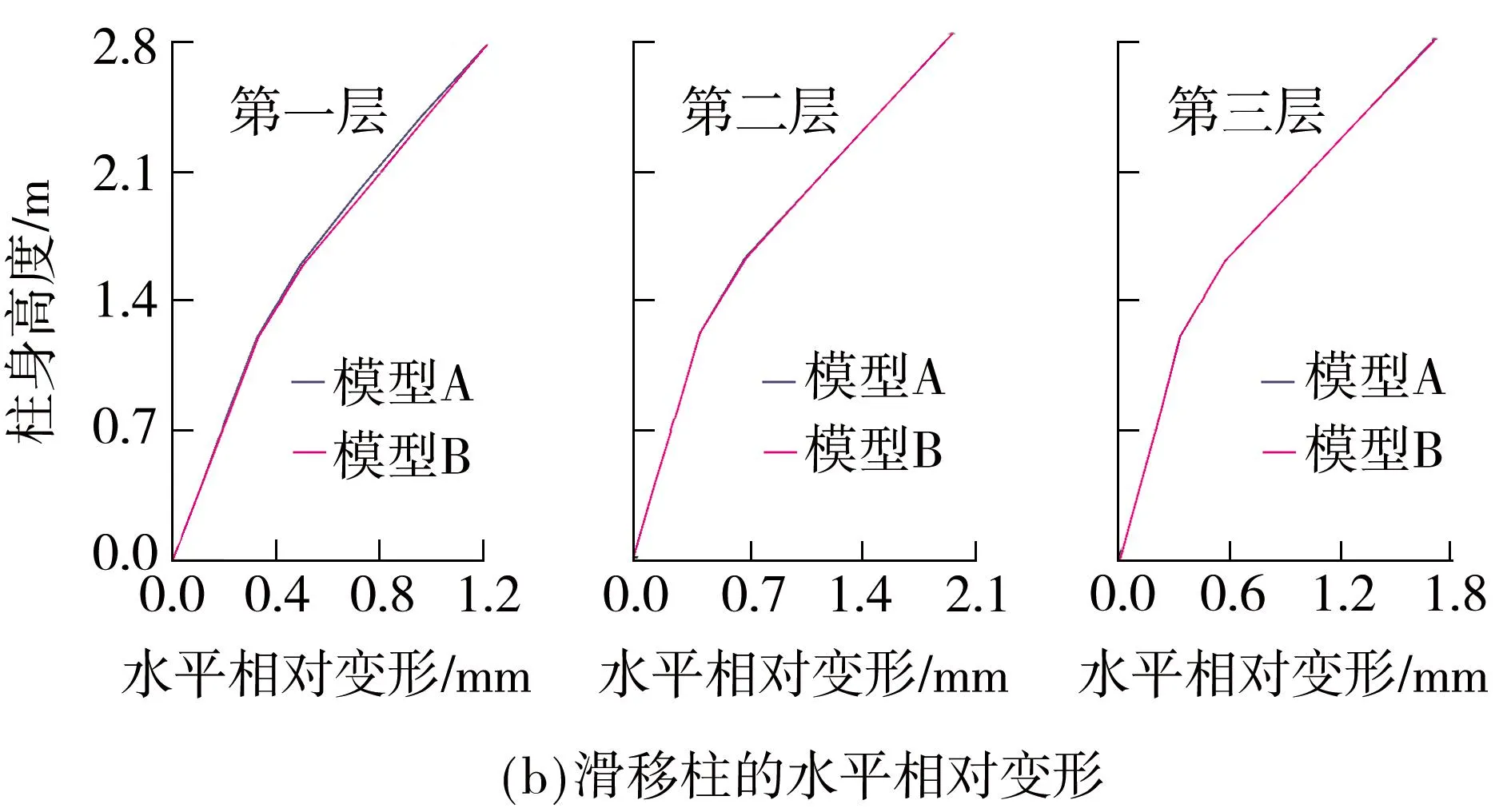
图3　模型A与B的计算结果对比

Fig.3Comparisons between calculation results of model A and model B

2无侧移滑移柱的弹性P-δ效应

2.1总弯矩分析

考虑图4所示无侧移滑移柱模型，其中下端转动约束刚度K由与该处相连的其他构件提供.外荷载包括轴力N和弯矩Mt，但后者仅有一部分由滑移柱承担，其余部分由与滑移柱下端相连的其他构件承担.此时，柱的平衡方程为

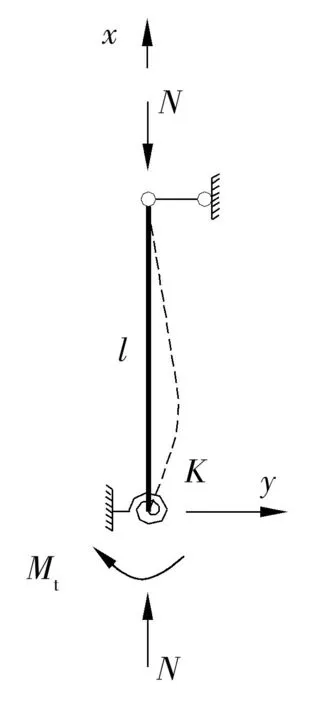
图4　无侧移滑移柱

(1)

式中:k2=N/EI，其中EI为柱截面的抗弯刚度；M为柱下端实际承担的总弯矩；l为柱的高度；x为沿着柱方向任意一点的坐标.利用边界条件和，可解得柱的挠曲线为

(2)

考虑柱下端的弯矩平衡，有

Ky′(0)+M=Mt

(3)

联立式(2)和(3)，可得

(4)

根据材料力学理论，柱身任意横截面处的总弯矩为-EIy″.据此，可求出柱身最大总弯矩处的坐标xmax为

(5)

(6)

在外弯矩Mt一定的情况下，由上述分析以及式(4)和(6)可以看出:

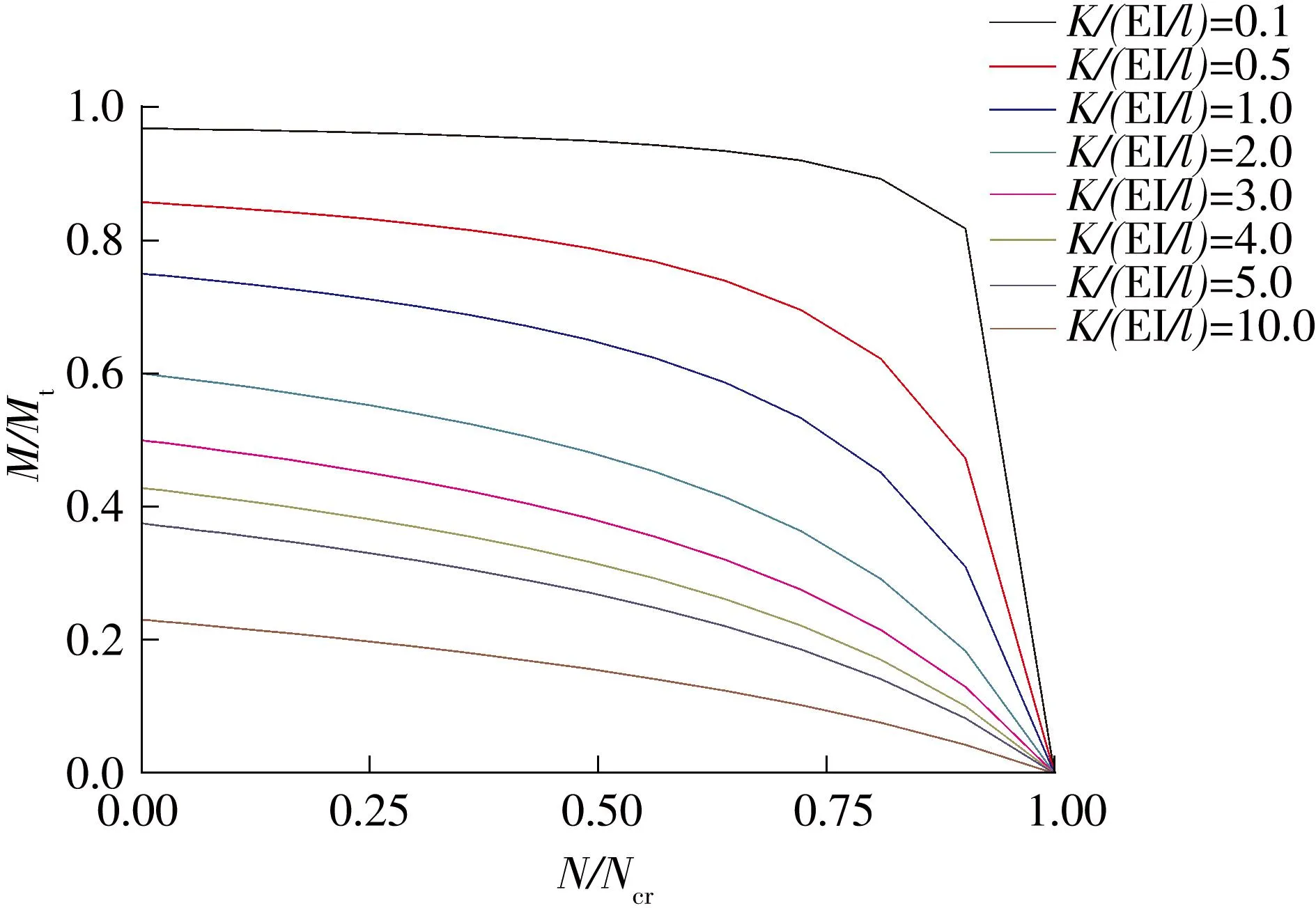
图5　M/Mt随N/Ncr的变化曲线

图6　Mmax/Mt随N/Ncr的变化曲线

2.2二阶弯矩分析

对于图4的无侧移滑移柱，其柱身任意横截面处的总弯矩为-EIy″，在此基础上扣除按结构力学理论推导出的式(7)所示一阶弯矩，即可得到柱身任意横截面处因P-δ效应引发的二阶弯矩，具体见式(8).

(7)

(8)

图7所示为不同情况下无侧移滑移柱的一阶弯矩、二阶弯矩、总弯矩示意图.针对不同参数情况，图8给出了无侧移滑移柱最大总弯矩处(即x=xmax处)的二阶弯矩与Mt之比.

从图7和8可以看出:

图7　无侧移滑移柱的弯矩示意图

Fig.7Schematic diagrams of bending moments for sliding co-

lumn without sidesway

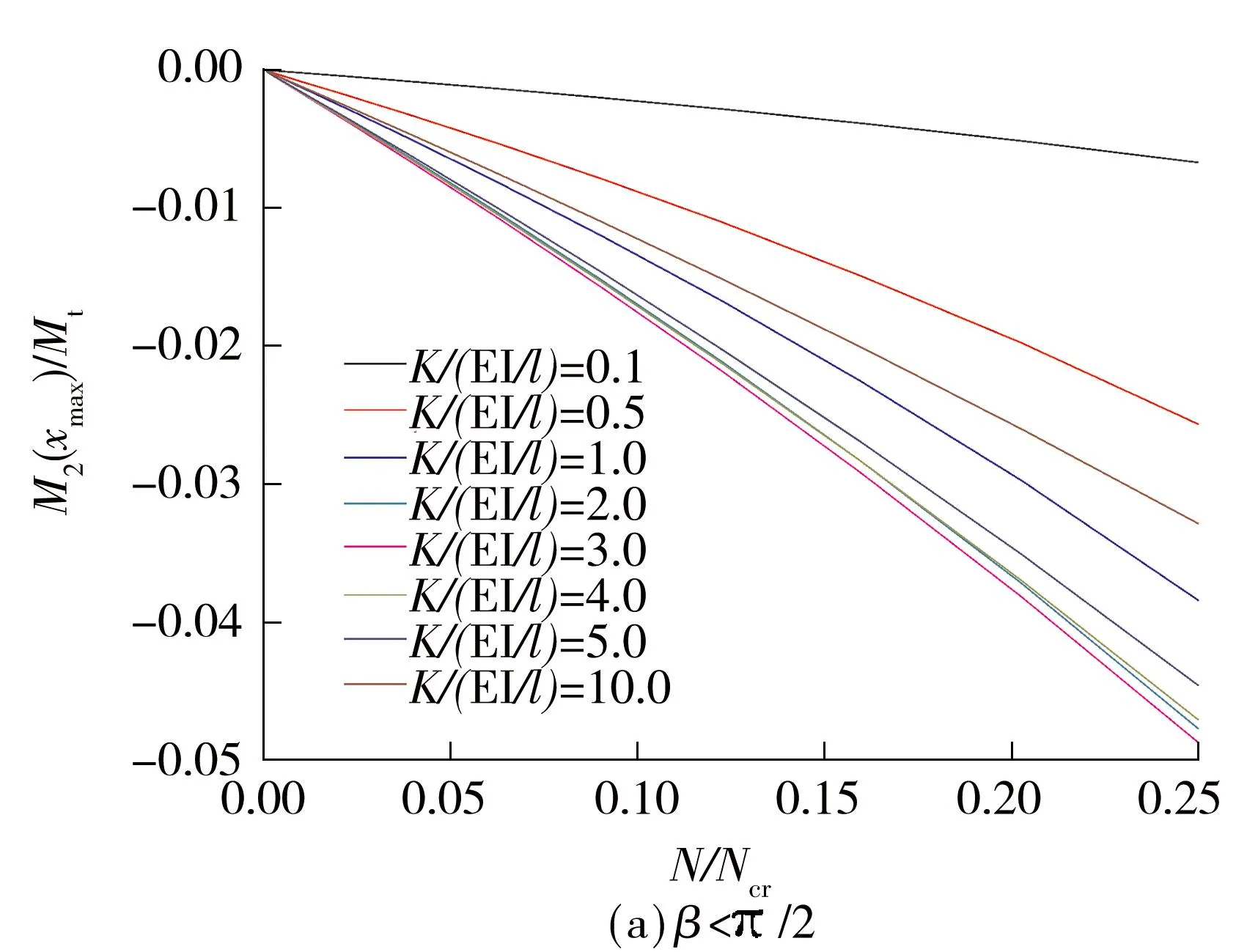
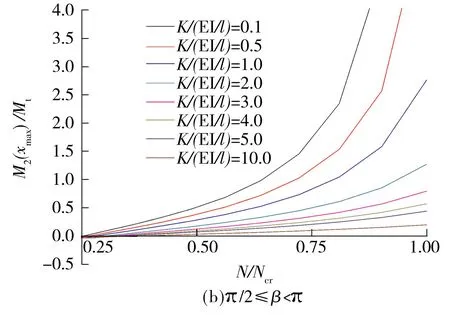
图8　无侧移滑移柱最大总弯矩处的二阶弯矩

Fig.8Secondary moment at the location related to maximum total moment for sliding column without sidesway

为确定情况1和情况2的界限，将式(8)中的x取为式(5)所示xmax，并令M2(xmax)/Mt等于0，可得

(9)

令式(8)等于0，可编程求得A点的坐标xA，于是柱有效长度l0=l-xA，且l0的大小与Mt无关.图9所示为不同参数情况下l0/l随N/Ncr的变化曲线.

图9　l0/l随N/Ncr的变化曲线

从图9中可以看出，l0/l对N/Ncr的改变不是很敏感.为方便实际设计，在编程计算结果的基础上，可回归给出l0的如下简便确定公式:

(10)

(11)

2.3K的确定

实际结构中某滑移柱的下端转动约束刚度可表示为

K=∑mbEbIb/lb

(12)

式中，Eb、Ib和lb分别为与滑移柱下端相连的某根梁的混凝土弹性模量、截面惯性矩和跨度，mb是与柱下端相连的某根梁的线刚度与该梁对柱下端提供的转动约束刚度的关系系数.需要注意的是，K的表达式与下层柱的刚度无关.这是因为滑移柱一般设置在各层的同一位置，而下层滑移柱的柱顶边界条件又可近似模拟为铰接，这样下层滑移柱就不提供转动约束了.mb的表达式为

(13)

式中:θi,1和θj,1分别为不考虑P-δ效应时，与滑移柱下端相连的某根梁的近端转角和远端转角；θi和θj分别为考虑P-δ效应时，与滑移柱下端相连的某根梁的近端转角和远端转角.θi,1/θj,1与θi/θj的差别仅仅源于柱二阶变形引发的梁转角变化，一般情况下该差别并不显著[9]，可不予考虑，即式(13)的第一式也可近似适用于考虑P-δ效应的情况.对于结构主要承受竖向荷载的情况，若假设梁两端的转角大小相等、方向相反，则有mb=2.

由于实际结构中某滑移柱考虑与不考虑P-δ效应时K的值近似相等，在对结构进行弹性分析求得该柱的一阶弯矩后，即可由式(11)计算弯矩放大系数η，进而获得该柱的最大总弯矩.

3无侧移滑移柱的非弹性P-δ效应

前述分析尚停留在弹性阶段，未考虑混凝土非线性的影响.参考MacGregor等对常规柱非弹性P-δ效应的研究成果[14- 16]，无侧移滑移柱的非弹性P-δ效应可按如下步骤分析:(1)利用弹性分析方法，求得柱的一阶弯矩；(2)考虑非弹性因素，对式(11)中的β和K/(EI/l)进行修正；(3)基于修正后的弯矩放大系数η和弹性一阶弯矩，获得柱考虑非弹性P-δ效应后的最大总弯矩.

3.1β的修正

计算β时涉及柱截面抗弯刚度EI，考虑混凝土裂缝、徐变以及应力-应变曲线非线性影响后，EI可用式(14)和(15)所示等效值EIe替代[16- 20]，它们给出的是柱截面抗弯刚度的下限值.柱配筋不多时，式(14)是合理的；柱配筋较高时，该式低估了钢筋的影响，此时采用式(15)较为准确.

(14)

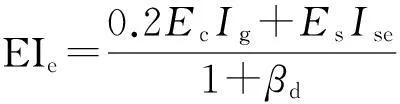
(15)

式中:Ec为柱混凝土弹性模量；Es为钢筋弹性模量；Ig为混凝土毛截面面积的惯性矩；Ise为钢筋对柱截面形心轴的惯性矩；βd为恒载轴力设计值与总轴力设计值之比，用以考虑徐变影响.

3.2K/(EI/l)的修正

K/(EI/l)的修正同时涉及柱截面抗弯刚度EI和梁截面抗弯刚度EIb，考虑非线性影响后它们的等效值应尽量接近实际情况，而不宜取下限值.借鉴MacGregor等的研究成果，分别对梁和柱的弹性刚度乘以折减系数0.4和0.8[21- 22]，据此可求得K/(EI/l)的修正值[K/(EI/l)]e，进而由式(10)可得l0/l的修正值.

4计算实例

4.1算例1

某部分柱顶滑移钢筋混凝土框剪结构的一阶弹性分析表明，小震作用下其基底重力附加弯矩不大于基底初始弯矩的10%，可不计入重力二阶效应的影响[23]，近似按无侧移结构考虑.该结构的一根滑移柱的柱高l=5.0 m，设计轴压比0.95，βd=0.6，柱下端一阶弯矩为M1.柱混凝土强度等级C40，柱截面500 mm×500 mm；与滑移柱下端相连的两根梁的混凝土强度等级C30，梁截面300 mm×700 mm，梁跨度8 m，考虑楼板影响的刚度增大系数为2.0.根据前文的分析，可得:EIe=42 318 kN·m2(按式(14)计算)，[K/(EI/l)]e=3.799，β=1.637，l0/l=0.862(按式(10)计算)，β<βcr(βcr=1.823)，此时不需考虑该滑移柱的P-δ效应.

4.2算例2

同一结构中的另一滑移柱，柱高l=9.0 m，其余参数同算例1.根据前文的分析，可得:EIe=42 318 kN·m2(按式(14)计算)，[K/(EI/l)]e=6.839，β=2.947，l0/l=0.832(按式(10)计算)，β>βcr=1.888，η=1.250，柱身最大总弯矩Mmax为1.250M1，而不考虑P-δ效应时柱身最大弯矩为M1，前者比后者增大25.0%.

5结论

(1)小震阶段滑移柱顶部的摩擦支座可采用普通铰进行近似处理，从而大大简化后续分析.

(4)利用式(11)所示弯矩增大系数，只需对无侧移滑移柱进行一阶弯矩分析，即可方便地确定其考虑P-δ效应后的柱身最大弯矩.

参考文献：

[1]吴波,黄仕香,赵新宇.混凝土框剪结构的落层倒塌碰撞试验 [J].工程力学,2012,29(6):176- 187.WU Bo,HUANG Shi-xiang,ZHAO Xin-yu.Experimental study on pancake collapse of RC frame-shear wall structures [J].Engineering Mechanics,2012,29(6):176- 187 .

[2]HAWKINS N M,MITCHELL D.Progressive collapse of flat plate structures [J].ACI Journal,1979,76(7):775- 808.

[3]ASTANEH-ASL A.Progressive collapse prevention in new and existing buildings [C]∥Proceedings of 9th Arab Structural Engineering Conference.Abu Dhabi:[s.n.],2003:1001- 1008.

[4]吴波,陈展图.抗倒塌柱顶部分滑移钢筋混凝土框架结构的初步研究 [J].地震工程与工程振动,2008,28(4):82- 87.

WU Bo,CHEN Zhan-tu.Preliminary study on RC frame structures with sliding at partial column upper ends for preventing collapse [J].Earthquake Engineering and Engineering Vibration,2008,28(4):82- 87 .

[5]吴波,吕文龙,熊伟.部分柱顶滑移钢筋混凝土框剪结构 [J].工程力学,2011,28(4):82- 88.

WU Bo,LÜ Wen-long,XIONG Wei.RC frame-shear wall structures with partial columns sliding at upper ends [J].Engineering Mechanics,2011,28(4):82- 88.

[6]吴波,吕文龙.部分柱顶滑移钢筋混凝土框剪结构的深化研究 [J].工程力学,2012,29(8):143- 149.

WU Bo,LÜ Wen-long.Research on RC frame-shear wall structures with partial columns sliding at upper ends [J].Engineering Mechanics,2012,29(8):143- 149.

[7]吴波,吕文龙,沈朝勇.部分柱顶滑移钢筋混凝土框剪结构的试验研究 [J].工程力学,2015,32(2):163- 170.WU Bo,LÜ Wen-long,SHEN Chao-yong.Experimental study on RC frame-shear wall structures with partial columns sliding at upper ends [J].Engineering Mechanics,2015,32(2):163- 170.

[8]魏巍,朱爱萍,刘毅,等.考虑P-δ效应的钢筋混凝土框架柱设计方法 [J].建筑结构学报,2006,27(5):64- 71.

WEI Wei,ZHU Ai-ping,LIU Yi,et al.Design methods of reinforced concrete frame column consideringP-δeffect [J].Journal of Building Structures,2006,27(5):64- 71.

[9]程光均,于海祥,白绍良,等.钢筋混凝土框架柱挠曲侧移二阶效应的整体考虑 [J].建筑结构,2006,36(7):44- 46.

CHENG Guang-jun,YU Hai-xiang,BAI Shao-liang,et al.Whole considering of second-order effect of flexure and displacement [J].Building Structure,2006,36(7):44- 46 .

[10]童岳生,童申家.钢筋混凝土偏心受压构件挠曲二阶效应计算方法 [J].工业建筑,2012,42(10):53- 57.

TONG Yue-sheng,TONG Shen-jia.Calculation method of flexural second-order effect for RC eccentrically compressed member [J].Industrial Construction,2012,42(10):53- 57.

[11]许晶,贡金鑫.无侧移钢筋混凝土柱荷载-变形特性及非线性二阶效应 [J].建筑结构学报,2012,33(5):93- 104.

XU Jing,GONG Jin-xin.Load-deflection characteristic and calculation of second-order effect of non-sway reinforced concrete columns [J].Journal of Building Structures,2012,33(5):93- 104.

[12]GB50010—2010,混凝土结构设计规范 [S].

[13]ACI318-11,Building code requirements for structural concrete and commentary [S].

[14]NILSON A H,DARWIN D,DOLAN C W.Design of concrete structures [M].New York:McGraw Hill Higher Education,2003.

[15]LAI S M A,MACGREGOR J G,Hellesland J.Geometric nonlinearities in nonsway frames [J].Journal of Structural Engineering,1983,109(12):2770- 2785.

[16]MACGREGOR J G,BREEN J E,PFRANG E O.Design of slender concrete columns [J].ACl Journal,1970,67(1):6- 28.

[17]MACGREGOR J G,OELHAFEN V H,HAGE S E.A reexamination of the EI value for slender columns [C]∥Reinforced Concrete Columns.Detroit:American Concrete Institute,1975:1- 40.

[18]TIKKA T K,MIRZA S A.Nonlinear EI equation for slender reinforced concrete columns [J].ACI Structural Journal,2005,102(6):839- 848.

[19]TIKKA T K,MIRZA S A.Equivalent uniform moment diagram factor for composite columns in minor axis bending [J].ACI Structural Journal,2006,132(10):1590- 1602.

[20]TIKKA T K,MIRZA S A.Nonlinear equation for flexural stiffness of slender composite columns in major axis bending [J].Journal of Structural Engineering,2006,132(3):387- 399.

[21]HAGE S E,MACGREGOR J G.Second order analysis of reinforced concrete frames [R].Edmonton:University of Alberta,1974.

[22]MACGREGOR J G.Design of slender concrete columns-revisited [J].ACI Structural Journal,1993,90(3):302- 309.

[23]GB50011—2010,建筑抗震设计规范 [S].

P-δEffect of Sliding Columns in Reinforced Concrete Structures with Partial Columns Sliding at Upper Ends

WUBo1LÜWen-long1,2

(1.State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, Guangdong,China; 2.Guangdong Provincial Academy of Building Research Group Co., Ltd., Guangzhou 510500, Guangdong, China)

Abstract:In order to reveal the P-δ effect of sliding columns in reinforced concrete structures with partial columns sliding at upper ends, the validity of a simplified model with upper end joints is verified. Then, the characteristics of the second-order moment of the sliding column without sidesway caused by the P-δ effect are investigated in different cases, the boundary condition considering the second-order moment is presented, and a method to determine the increment coefficient of the bending moment for the sliding column without sidesway is proposed. Moreover, the concrete nonlinearity is taken into account primarily by amending the parameters in the proposed method, and some examples are finally analyzed. It is found that the friction support located at the upper end of the sliding column under minor earthquakes can be approximately treated as a joint; and that, in some cases, the column's maximum bending moment increases owing to the second-order moment of the sliding column without sidesway caused by the P-δ effect and that it can be easily determined by using the first-order moment of the sliding column without sidesway and the aforementioned increment coefficient.

Key words:reinforced concrete structure;sliding at column upper end;P-δ effect; bending moment; increment coefficient

doi:10.3969/j.issn.1000-565X.2016.02.001

中图分类号：P 315.95

文章编号：1000- 565X(2016)02- 0001- 07

作者简介：吴波(1968-)，男，博士，研究员，主要从事结构抗灾和新型混凝土结构研究.E-mail:bowu@scut.edu.cn

*基金项目：国家自然科学基金资助项目(90815012,51438007)；亚热带建筑科学国家重点实验室自主研究课题(2013ZB24)

收稿日期：2015- 05- 11

Foundation items: Supported by the National Natural Science Foundation of China(90815012,51438007)