“化错教学法”的时机选择
2016-05-08李培芳
李培芳
华应龙老师依据多年的教学经验,提出了“化错教育”的主张。其研究成果给予小学数学教师一种行之有效的教学法,那就是“化错教学法”。
那么,普通教师在教学实践中如何进行“化错教学”呢?本文仅就“化错教学”的时机选择谈点自己的看法。
一、及时“化错”
一般地,“化错”时机越早越好,因为“错例”搁置越长时间,学生越容易生发认知形成记忆,将“错”第一时间消除,让学生建立正确的认知至关重要。下面以笔者执教的《等量关系》一课的一个教学片断为例加以阐述。
教师首先出示下面三个题目:
1.妈妈的体重是50千克,爸爸的体重是妈妈的2倍,求爸爸的体重。
2.妈妈35岁,爸爸的年龄比妈妈多3岁,爸爸几岁?
3.爸爸的收入比妈妈的2倍多500元,妈妈的收入是3000元,爸爸的收入是多少元?
师:既然等量关系这么重要,那么,咱们就要学会在问题解决中找出等量关系,请同学们找一找哪一句反映出数量间相等的关系。
生:题1“爸爸的体重是妈妈的2倍”反映出数量间相等的关系。
生:题2“爸爸的年龄比妈妈多3岁”反映出数量间相等的关系。
生:题3的等量关系是“爸爸的收入比妈妈的2倍多500元”。
师:其中题3的等量关系你是怎么理解的,你能不能把你对这个等量关系的理解用“图”或者“式子”表示出来。
学生自主尝试后,展示交流:
方法1:妈妈的收入×2+500=爸爸的收入
方法2:爸爸的收入×2+500=妈妈的收入
方法3:爸爸的收入÷2-500=妈妈的收入
方法4:画线段图(如下图)。
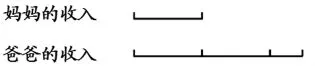
师:同学们,对于这几种方法,你认为这其中哪些是对的,哪些是错的?说说你的看法。
生1:方法2是错的,从图中就可以看出来了,爸爸的收入再乘2,那就很长了。
生2:方法3也是错的,正确的应该是:(爸爸的收入-500)÷2=妈妈的收入。
师:(追问)能说说为什么吗?
生2:从图中可以看出来,(爸爸的收入-500)就刚好是妈妈收入的2倍。
师:比较一下,咱们会发现线段图能很清楚地反映出数量相等的关系,相比于式子,线段图更——
生:直观。
师:说得好,直观是什么意思知道吗?
生:直观就是可以“直接地看出来”。
师:说得真好,佩服,佩服!
在这一教学片断中,由于有了支撑解释“错误之因”的线段图,“化错”来得及时,及时的“化错”杜绝了学生的错误认知,对于他们正确理解与表达此类数量关系有直接的帮助。
二、延时“化错”
前文说到“化错”应当及时,然而凡事不绝对,有时候学生现有的认知不足于理解“正确”,或者现有的例子不足以解释“正确”,教师则宜将“错误”搁置,留待更好的时机“化错”。
试看华应龙老师执教《找次品》时的一个精彩片断:
师:接下来,多点吧,从8个球中找,好吗?怎么找?
生:每边放4个,因为8个当中只有一个是重球,所以一定不平衡。下沉的那边肯定有重球。接下来就是把重的那4个继续称,每边放2个……
师:真好,谢谢你!这其实让我们探讨一个问题,接下来是……从4个中找,怎么找?大家可以一起说吧!
生:(齐)每边放 2个,一定会有一边下沉。
师:很好,“一定”这个词用得好!一定不平衡,重球在——
生:(齐)重球在下沉的那边。接下来就是从2个里面找……
师:好,称几次肯定能找到?
生:(齐)3次。
师:对!接着,请问,9个球中有一个重球,怎么找?独立思考后小组交流。
生:也是称3次。先每边放4个球,还有一个放在旁边。如果是平衡的,那么放在旁边的就一定是重球了。如果不平衡,接下来就是从4个中找。从4个中找,刚才研究过了,要称2次。这样,一共要称几次?
生:(齐)3次。
师:好极了,小老师做得好!有补充吗?
生:如果平衡的话,只称了1次。
生:那是运气好的特殊情况,不能算。
师:我欣赏这样的对话!还有没有不同的称法吗?
生:先每个盘子各放3个球,还有3个球放在外面。如果平衡的话,重球就在第三个盘子里。
师:“在第三个盘子里”,说得好!
生:如果是不平衡的话,重球是在下沉的那个盘子里,接下来也是从3个中找。从3个中找,已经研究过了,再称1次就行。这样,一共称几次啊?
生:(齐)2次。
师:掌声奖励!(指着板书)同样是9个球,一种称3次,一种称2次。请问,称2次是不是也是运气好的情况呢?
生:(齐)不是。
师:为什么不是运气最好的情况呢?
生:因为它是分成3个在一个盘子里的,不管平衡还是不平衡,接下来都是从3个里找,所以这是确保是2次的。
师:同意吧?掌声!也就是说,当我们不是把9分成(4,4,1),而是平均分成(3,3,3)的时候,不管平衡还是不平衡,都是2次能确保称出来。
师:(指板书——8个球,3次;9个球,2次)有问题吗?这么多人能发现问题,真棒!
生:为什么球的数量变多了,次数反而变少了呢?
师:好问题!为什么?
生:其实,8个球也是可以用2次称出来的。
师:从8个球中找,最少2次也能找出来?你暂且不说,好不好?让其他同学也想想。
(发言的男生自豪地点点头)
师:真好!心领神会,心心相印,掌声给他!有研究发现,能憋着的人,因为心中有他人,更容易成功。请大家都琢磨一下,8个球,怎么2次把重球找出来?可以在脑子里面想,可以在纸上想。请最后面的女生——
生:每边放3个,外面还有2个。如果平衡的话,那就是外面2个中有一个是稍重的;如果不平衡的话,那接下来就是从3个中找。不管从2个中找,还是从3个中找,只要1次就可以了。这样一共只要称2次。
(全班响起热烈的掌声)
师:你真是一个很有智慧的女孩,掌声再次给她。第一次发言就能赢得我们两次掌声,非常棒!我们掌声继续给开始不明白,现在经过自己努力搞明白的同学,你们是进步最大的人!
师:现在,我们知道了8个球中找,最少2次就能称出来了。原来我们研究8个的时候没再琢磨一下,会不会有其他的可能呢?所以我非常欣赏那个男孩,那个男孩当时举手了,我只是想让全班同学都经历这个过程,所以我没请他回答,他那会儿就憋着了,手已经放下去了,掌声再次给他。你是我的托儿,真好!
这一教学片断中,学生一开始认为从8个球中找出次品(较重)需要3次,华老师没有指出错误,学生也没有发现错误,这个错误被自然而然地搁置了下来,被华老师智慧地“隐藏”了起来,而当学生探索得出9个球仅需2次时,华老师引导学生发现了问题“为什么数量多了,次数反而少了呢”这个问题是极其有力量的一个问题,它让学生重新审视之前的想法,这种反思是可贵的,这种自发发现错误进而矫正的学习体验更有力量,它冲击的是学生已有的思维,并在错误的思维点上发力,让学生印象深刻、体验深切。
