单群L2(8)的一个特征性质

郭继东,　任永才,　张志让

(　　　1. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000;　2. 四川大学 数学学院, 四川 成都 610064;

3. 成都信息工程学院 数学学院, 四川 成都 610225)



单群L2(8)的一个特征性质

郭继东1,任永才2,张志让3

(1. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000;2. 四川大学 数学学院, 四川 成都 610064;

3. 成都信息工程学院 数学学院, 四川 成都 610225)

摘要：展示单群L2(8)的一个特征性质,证明定理:如果有限群G的同阶的元素的个数组成的集合是{1,63,56,216,168},则G≅L2(8).

关键词：有限群; 单群; 元素的阶; 同阶元的个数

记Md(G):={g∈G|gd=1}.称有限群G1和G2是同阶型的,如果|Md(G1)|=|Md(G2)|,d=1,2,….1987年，J. G. Thompson在给施武杰的一封信中提出了下述问题[1]:

Thompson问题设G1和G2是同阶型的.如果G1是可解的,G2是否可解?

Thompson问题自1990年公开以来一直没有得到解决.

对于有限群G,用SOENS(G)表示G中的同阶的元素的个数组成的集合.例如,SOENS(L2(8))={1,63,56,216,168}.对于有限群G1和G2,如果G1和G2是同阶型的,则显然有|G1|=|G2|且SOENS(G1)=SOENS(G2).于是,产生了Thompson问题的一个变种,在这里姑且称为Thompson猜想:

Thompson猜想设M是个有限非Abel单群,G是个有限群.如果

则G≅M.

关于上述Thompson猜想以及别的类似的Thompson猜想的研究,例如见文献[2-3].这里感兴趣的是,Thompson猜想中的“|G|=|M|”这一条件是否可以去掉?对某些单群回答是肯定的.例如,令M=L2(8),则|G|=|M|这一条件可以去掉.本文目的就是证实这一断言,即证明下述定理:设G是个有限群.如果SOENS(G)={1,63,56,216,168},即如果SOENS(G)=SOENS(L2(8)),则G≅L2(8).

注SOENS(G)={n1,…,nt}一般说来不意味着|G|=n1+…+nt.

本文中的群都是指有限群.字母G总是代表一个群.π(G)是|G|的的全体素因子组成的集合.对于p∈π(G),用Sylp(G)表示G的全体Sylowp-子群组成的集合,用Gp代表G的一个Sylowp-子群.用πe(G)表示G的元素的阶组成的集合.用nm表示G中的m阶元的个数.此外,对符号|作一说明:|G||100表示|G|除尽100.文中其它未说明的符号都是标准的,例如见文献[4-5].

1预备引理

从若干引理开始.下述引理1引自文献[6].

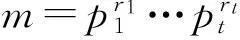
此外,如果m>2,则φ(m)是偶数(φ是Euler Phi-函数).(在后面的论证中将不指明地使用引理1.)

下述引理2(i)是众所周知的,由引理1和引理2(i)得到引理2(ii)和引理2(iii).

引理 2对于群G,下述3个命题成立:

(i)nm=kφ(m),其中k是G的m阶循环子群的个数(m阶循环群中的m阶元(即生成元)的个数是φ(m));

(ii) 如果m>2,则nm是偶数;

(iii) 若nm是奇数,则m=2,G是偶数阶群.

下述引理3是一个初等结果[7].

引理 3对于群G,下述两个命题成立:

(i) 设m是|G|的因子,则m||{g∈G|gm=1}|.

(ii) 如果p是|G|的一个素因子,则p|(1+np).

下述引理4也是一个初等结果(见文献[7]).

引理 4设P是个pn阶初等Abel群,p是素数.那么,|Aut(P)|=pn-1(p-1)…(pn-1).

下述引理5是文献[8]中的定理9.3.1的(4)式的特殊情形.

说G是一个单K3-群,如果G是一个单群且|π(G)|=3.

引理 6[9]设M是一个单K3-群.那么M与下述群之一同构A5、A6、L2(7)、L2(8)、L2(17)、L3(3)、U3(3)和U4(2).

表 1

定义 1设SOENS(G)={m1=1,m2,…,mt}.令

下述引理7是引理3(ii)的直接推论.

引理 7π(G)⊆π(SOENS(G)+1).

2主要结果

现在着手证明本文的主要结果,即证明下述定理1.注意,SOENS(L2(8))={1,63,56,216,168}.

定理 1如果SOENS(G)={1,63,56,216,168},则G≅L2(8).

证明为便于对照察看,在下面列出2个表格.第1个表格(表2)的第1行中的数是SOENS(G)中的数,而第2行中的各个乘积是它正上方的数的素因子分解式.第2个表格(表3)的第1行中的数是SOENS(G)+1中的数,而第2行中的各个乘积是它正上方的数的素因子分解式.

表 2　SOENS(G)

表 3　SOENS(G)+1

由表3得到

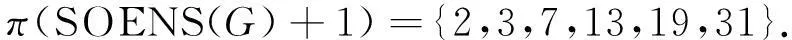
下面分若干步骤完成定理的证明.

(I) |G|≥504(显然).

(II) 下述事实成立:(a) 2∈π(G)且n2=63;(b) 如果3∈π(G),则n3=56;(c) 如果7∈π(G),则n7=216.

证明根据引理2知(a)成立.根据引理3和表3知(b)和(c)成立.

(III) 下述事实成立:(a) 13∉π(G);(b) 19∉π(G);(c) 31∉π(G).

(IV)π(G)⊆{2,3,7}.

证明根据引理7和前面关于π(SOENS(G)+1)的等式及(II)和(III)得到π(G)⊆{2,3,7}.

(V) (根据(II)(a)可)写|G|=2n·r,其中n和r是正整数且(2,r)=1.那么,n≤6.

证明由于φ(25)=24,根据引理2和表2有25∉πe(G).

如果2t∈πe(G),其中t=2,3,4,则由于φ(2t)=2t-1,根据引理2和表2得到n2t∈{56,216,168}(t=2,3,4).

总上述,得到n≤6.

(VI) 设|G|=3m·r,其中m和r是正整数且(3,r)=1.那么,m≤2,并且,如果m=2,则

证明由于φ(35)=2·34,根据引理2(i)并察看表2可知n35∉πe(G).同时,由于φ(3t)=2·3t-1,从表2还看到:如果3t∈πe(G))(t=2,3,4),则n3t∈{216,168}.

假设m=2.那么,由上一段知道32∈πe(G).于是,G的Sylow 3-子群是32阶循环群.从而,由于n32=168及φ(32)=2·3,根据引理2得到

所以,根据(II)(a)和(IV)得到π(G)={2,3,7}.

(VII) 设|G|=7f·r,其中f和r是正整数且(7,r)=1.那么,f=1(即|G7|=7),|Syl7(G)|=36=22·32,|G|=2n·32·7.此外,G没有14阶元.

(VIII)G不是2-群.

证明如果G是2-群,则根据(V)有|G|≤26=64,与(I)矛盾.

(IX)π(G)≠{2,3}.

证明假设π(G)={2,3}.那么,|G|=2n·3m.根据(V)和(VI)有n≤6,m≤2.于是,根据(I)有|G|=26·32,从而根据(VI)得π(G)={2,3,7},矛盾.

(X)G≅L2(8).

由(II)(a)、(IV)、(VIII)、(X)和(VII)可知:|G|=2n·32·7,n≤6,|Syl7(G)|=22·32.于是,有|NG(G7)|=2n-2·7.

由于|G|=2n·32·7及|Syl7(G)|=22·32,根据引理5知G是非可解的.令K是G的极大可解正规子群.那么,G/K是非可解的.令N/K是G/K的一个极小正规子群.那么,N/K是若干个同构的非Abel的单群的直积(见文献[10]).于是,N/K显然是个单K3-群,从而根据引理6和表1知:要么N/K≅L2(7),要么N/K≅L2(8).

2) 设N/K≅L2(8).这时,有L2(8)≅N/K≤G/K≤Aut(N/K)=Aut(L2(8)).从而,根据文献[11]知道:G/K≅L2(8)或G/K≅PΓL2(8).于是,由于33||PΓL2(8)|而33除不尽||G|,有G/K≅L2(8).从而,|K|=2n-3.

假设n>3.由于n≤6见(V))且G没有14阶元(见(VII)),根据引理4和阶≤23的群的结构断定K是8阶初等Abel 2-群.于是,由于G/K≅L2(8)是单群且G没有14阶元,根据引理4知道:23·32·7|22·3·7,矛盾.所以,n=3,|K|=1,G=N≅L2(8).证毕.

参考文献

[1] 沈如林,施武杰. 关于Thompson问题[J]. 中国科学:数学,2010,40(3):533-537.

[2] 邵长国,施武杰,蒋琴会. 单K3-群的一个特征性质[J]. 数学进展,2009,38(3):327-330.

[3] CHEN G Y. On Thompson’s conjecture[J]. J Algebra,1996,185:184-193.

[4] ROSE H E. A Course on Finite Groups[M]. London:Springer-Verlag,2009.

[5] ISAACS I M. Character Theory of Finite Groups[M]. Providence:AMS,2006.

[6] LANG S. Algebra[M]. NJ:Addison Publishing Company,1984.

[7] HUPPERT B. Endlich Gruppen I[M]. New York:Springer-Verlag,1967.

[8] HALL M. Theory of Groups[M]. New York:Macmillan Company,1959.

[9] GORENSTEIN D. Finite Simple Groups[M]. New York:Plenum Press,1982.

[10] ROSE J S. A Course on Group Theory[M]. Cambridge:Cambridge University Press,1978.

[11] Conway J H, Curtis R T, Norton S P, et al. Atlas of Finite Groups[M]. Oxford:Clarendon Press,1985.

[12] HUPPERT B. Character Theory of Finite Groups[M]. Berlin:Walter de Gruyter,1998.

[13] 余大鹏,张良才.L7(3)与GL7(3)的刻画[J]. 数学年刊,2012,A33(5):599-608.

[14] MOGHADAMFAR A R, ZOKAYI A K. OD-characterization of certain finite groups having connected prime graph[J]. Algebra Colloq,2010,17(1):121-130.

2010 MSC：20D15; 20C15

(编辑周俊)

A Characterization of the Simple GroupL2(8)

GUO Jidong1,REN Yongcai2,ZHANG Zhirang3

(1.CollegeofMathematicsandStatistics,YiliNormalCollege,Yining835000,Xinjiang;2.SchoolofMathematics,SichuanUniversity,Chengdu610064,Sichuan;3.SchoolofMathematics,ChengduUniversityofInformationTechnology,Chengdu610225,Sichuan)

Abstract：In this paper, a characterization of the simple group L2(8) is given as follows: Let G be a finite group. If the set of the numbers of the same order elements in G is {1,63,56,216,168}, then G≅L2(8).

Key words：finite group; simple group; the number of the same order elements

doi:10.3969/j.issn.1001-8395.2016.01.019

中图分类号：O152

文献标志码：A

文章编号：1001-8395(2016)01-0107-04

作者简介：郭继东(1965—),男,教授,主要从事群论研究,E-mail:guojd662@163.com

基金项目：新疆维吾尔自治区普通高等学校重点学科基金(2012ZDXK12)

收稿日期:2014-09-27